1.2.4.1 绝对值 课件(共19张PPT)
文档属性
| 名称 | 1.2.4.1 绝对值 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 07:08:16 | ||
图片预览




文档简介
(共19张PPT)
第一章
有理数
1.2.4
第1课时
绝对值的定义和性质
随堂演练
课堂小结
获取新知
情景导入
例题讲解
知识回顾
知识回顾
1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
0
1
2
-1
-2
2、什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
数轴的三要素
情景导入
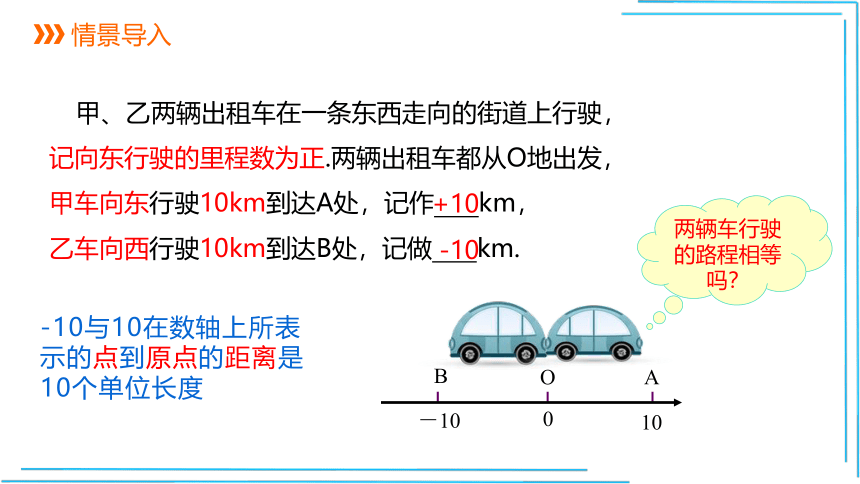
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作
km,
乙车向西行驶10km到达B处,记做
km.
+10
-10
两辆车行驶的路程相等吗?
-10
10
0
O
B
A
-10与10在数轴上所表示的点到原点的距离是10个单位长度
获取新知
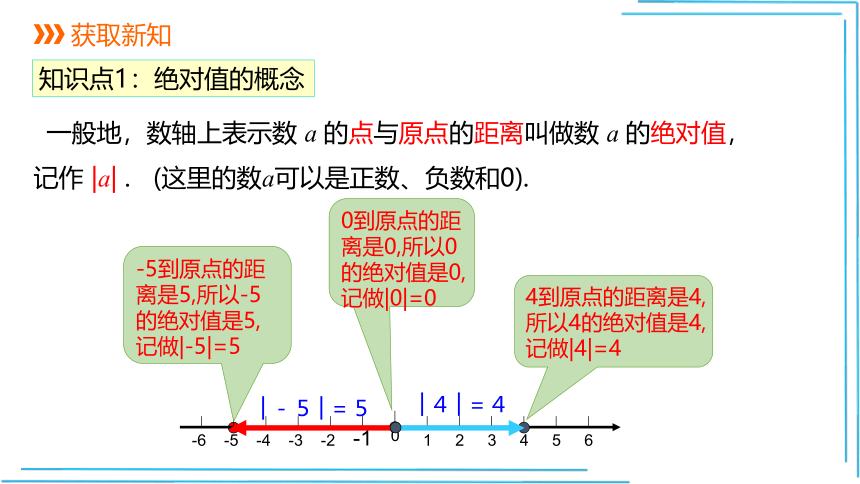
一般地,数轴上表示数
a
的点与原点的距离叫做数
a
的绝对值,记作
|a|
.
(这里的数a可以是正数、负数和0).
知识点1:绝对值的概念
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
0
0
0
0
0
5
3.5
-3
-4.5
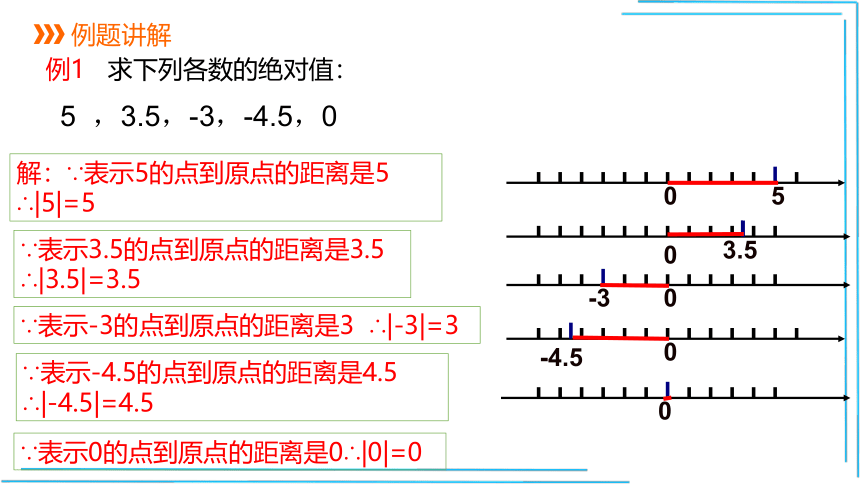
例题讲解
例1
求下列各数的绝对值:
5
,3.5,-3,-4.5,0
解:∵表示5的点到原点的距离是5
∴|5|=5
∵表示3.5的点到原点的距离是3.5
∴|3.5|=3.5
∵表示-3的点到原点的距离是3
∴|-3|=3
∵表示-4.5的点到原点的距离是4.5
∴|-4.5|=4.5
∵表示0的点到原点的距离是0∴|0|=0
思考:
一个正数的绝对值是
一个负数的绝对值是
0的绝对值是
问题:观察这些表示绝对值的数,它们有什么共同点?
|5|=5
|3.5|=3.5
|-3|=3
|-4.5|=4.5
|0|=0
知识点2:绝对值的性质
它本身
它的相反数
0
用式子表示为:
备注:任何有理数的绝对值都是非负数,即
问题:相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
|-5|=5
|+5|=5
互为相反数,符号相反
绝对值相等
例题讲解
例2
求下列各数的绝对值.
12,
-7.5,
0.
|12|=12;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
解:
例3.若整数a,b满足等式
,求a+b的值
解:
因为
所以a-3=0
,b-2=0
所以a=3,b=2
所以a+b=3+2=5
随堂演练
1.
下列说法正确的是( )
A.|-3|是求-3的相反数
B.|-3|表示的意义是数轴上表示-3的点到原点的距离
C.|-3|的意义是表示-3的点到原点的距离是-3
D.以上都不对
B
2.
的相反数是( )
A.
B.-
C.3
D.-3
B
3.绝对值不大于3.1的整数有(
)个
A.4
B.5
C.6
D.7
D
C
4.
下列各式中,不成立的是(
)
A.|3|=3
B.-|3|=-3
C.-|-3|=3
D.|-3|=|3|
5.
如果
+|b-1|=0,那么a+b=( )
A.
B.
C.
D.1
C
6.____的相反数是它本身,
_______的绝对值是它本身,
_______的绝对值是它的相反数.
0
非负数
非正数
7.求列各数的绝对值
:
,4,0,
.
解:
8.正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
问题:
指出哪个排球的质量好一些,并用绝对值的知识加以说明.
答:第五个排球的质量好一些,因为它的绝对值最小,也就是离标准质量的克数最近.
课堂小结
绝对值
几何意义:
数轴上表示这个数的点到原点的距离
代数意义:
零的绝对值是零.
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
绝对值的非负性:
|a|≥0
绝对值与相反数的关系:
互为相反数的两个数的绝对值相等.
https://www.21cnjy.com/help/help_extract.php
第一章
有理数
1.2.4
第1课时
绝对值的定义和性质
随堂演练
课堂小结
获取新知
情景导入
例题讲解
知识回顾
知识回顾
1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
0
1
2
-1
-2
2、什么是相反数?
只有符号不同的两个数叫做互为相反数.
规定:0的相反数是0.
数轴的三要素
情景导入
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作
km,
乙车向西行驶10km到达B处,记做
km.
+10
-10
两辆车行驶的路程相等吗?
-10
10
0
O
B
A
-10与10在数轴上所表示的点到原点的距离是10个单位长度
获取新知
一般地,数轴上表示数
a
的点与原点的距离叫做数
a
的绝对值,记作
|a|
.
(这里的数a可以是正数、负数和0).
知识点1:绝对值的概念
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
0
0
0
0
0
5
3.5
-3
-4.5
例题讲解
例1
求下列各数的绝对值:
5
,3.5,-3,-4.5,0
解:∵表示5的点到原点的距离是5
∴|5|=5
∵表示3.5的点到原点的距离是3.5
∴|3.5|=3.5
∵表示-3的点到原点的距离是3
∴|-3|=3
∵表示-4.5的点到原点的距离是4.5
∴|-4.5|=4.5
∵表示0的点到原点的距离是0∴|0|=0
思考:
一个正数的绝对值是
一个负数的绝对值是
0的绝对值是
问题:观察这些表示绝对值的数,它们有什么共同点?
|5|=5
|3.5|=3.5
|-3|=3
|-4.5|=4.5
|0|=0
知识点2:绝对值的性质
它本身
它的相反数
0
用式子表示为:
备注:任何有理数的绝对值都是非负数,即
问题:相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
|-5|=5
|+5|=5
互为相反数,符号相反
绝对值相等
例题讲解
例2
求下列各数的绝对值.
12,
-7.5,
0.
|12|=12;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
解:
例3.若整数a,b满足等式
,求a+b的值
解:
因为
所以a-3=0
,b-2=0
所以a=3,b=2
所以a+b=3+2=5
随堂演练
1.
下列说法正确的是( )
A.|-3|是求-3的相反数
B.|-3|表示的意义是数轴上表示-3的点到原点的距离
C.|-3|的意义是表示-3的点到原点的距离是-3
D.以上都不对
B
2.
的相反数是( )
A.
B.-
C.3
D.-3
B
3.绝对值不大于3.1的整数有(
)个
A.4
B.5
C.6
D.7
D
C
4.
下列各式中,不成立的是(
)
A.|3|=3
B.-|3|=-3
C.-|-3|=3
D.|-3|=|3|
5.
如果
+|b-1|=0,那么a+b=( )
A.
B.
C.
D.1
C
6.____的相反数是它本身,
_______的绝对值是它本身,
_______的绝对值是它的相反数.
0
非负数
非正数
7.求列各数的绝对值
:
,4,0,
.
解:
8.正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
问题:
指出哪个排球的质量好一些,并用绝对值的知识加以说明.
答:第五个排球的质量好一些,因为它的绝对值最小,也就是离标准质量的克数最近.
课堂小结
绝对值
几何意义:
数轴上表示这个数的点到原点的距离
代数意义:
零的绝对值是零.
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
绝对值的非负性:
|a|≥0
绝对值与相反数的关系:
互为相反数的两个数的绝对值相等.
https://www.21cnjy.com/help/help_extract.php
