【人教七上数学教学课件】1.4.1 第1课时 有理数的乘法法则 课件(共27张PPT)
文档属性
| 名称 | 【人教七上数学教学课件】1.4.1 第1课时 有理数的乘法法则 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 14:21:45 | ||
图片预览








文档简介
(共27张PPT)
第一章
有理数
1.4.1
第1课时
有理数的乘法法则
随堂演练
课堂小结
获取新知
情景导入
例题讲解
知识回顾
知识回顾
计算:
(1)3+3+3+3;
(2)(-5)+(-5)+(-5);(3)(-5)×3
解:
(1)3+3+3+3=3×4=12;
(2)(-5)+(-5)+(-5)=-15;
(3)
(-5)×3
=?
.
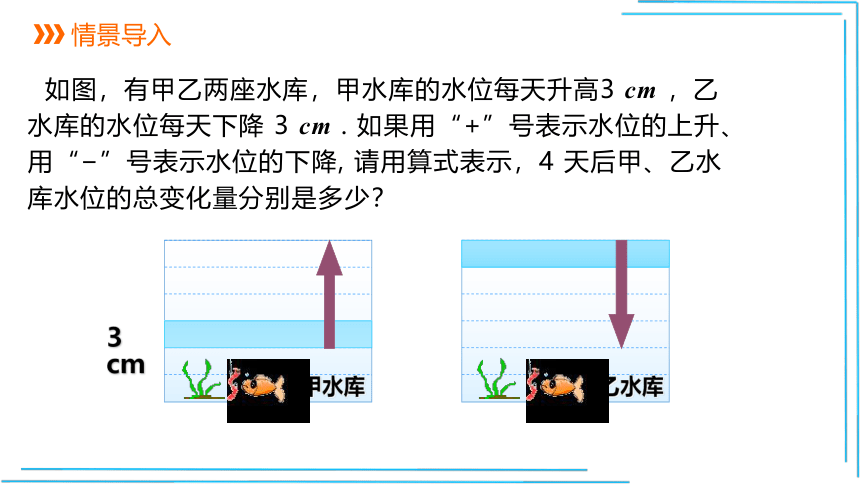
如图,有甲乙两座水库,甲水库的水位每天升高3
cm
,乙水库的水位每天下降
3
cm
.
如果用“+”号表示水位的上升、用“?”号表示水位的下降,
请用算式表示,4
天后甲、乙水库水位的总变化量分别是多少?
甲水库
乙水库
3
cm
情景导入
获取新知
(1)a.观察下面的乘法算式,你能发现什么规律?
3×3=9,
3×2=6,
3×1=3,
3×0=0.
规律:
随着后一乘数逐次递减1,
.
积逐次递减3
b.
要使这个规律在引入负数后仍然成立,那么应有:
3×(-1)=
-3,
3×(-2)= ,
3×(-3)= .
-6
-9
c.
观察下面的算式,你又能发现什么规律?
3×3=9,
2×3=6,
1×3=3,
0×3=0.
随着前一乘数逐次递减1,积逐次递减3.
d.
要使c中的规律在引入负数后仍成立,那么应有:
(-1)×3= ,
(-2)×3= ,
(-3)×3= .
-3
-6
-9
归纳如下:
正数乘正数,积为正数;
正数乘负数,积是负数;
负数乘正数,积也是负数.
积的绝对值等于各个乘数绝对值的积.
(2)对于以上问题,以小组为单位进行观察总结归纳.你能得出正数乘正数、正数乘负数、负数乘正数的规律吗?
(3)利用(2)中结论计算下面的算式,你又发现了什么规律?
(-3)×3= ,
(-3)×2= ,
(-3)×1= ,
(-3)×0= .
-9
-6
-3
0
随着后一乘数逐次减1,积逐次增加3
(4)按照(3)中的规律,并总结归纳.
(-3)×(-1)= ,
(-3)×(-2)= ,
(-3)×(-3)= .
3
6
9
积为正数,乘积的绝对值等于各乘数绝对值的积.
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
讨论:
(1)若a<0,b>0,则ab
0
;
(2)若a<0,b<0,则ab
0
;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
例题讲解
(2)8×(-1)=-(8×1)=-8.
解:(1)(-3)×9=-(3×9)=-27.
(1)(-3)×9;(2)8×(-1);
例1
计算:
(3)(
)×(-2)=+(
×2
)=1.
从(2)中可以看出,
要得到一个数的相反数,只要将它乘-1
(3)中两个数的乘积是1,这样的两个数有什么特殊关系呢?
(3)(
)×(-2).
备注:
有理数乘法的求解步骤是
先确定积的符号
再确定积的绝对值
找特点,给这些数起一个你喜欢的名字.
1
1
1
认真观察每一对数,你发现了么?
两个乘数的分子
分母互相颠倒.
如果两个数的乘积是1,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数.
例2
求下列各数的倒数:
(1)
;(2)-1;(3)
;(4)0.125.
解:(1)
的倒数是
(2)-1
的倒数是-1
(3)
的倒数是
(4)0.125的倒数是8
要点精析:
(1)0没有倒数.
(2)一个数和它的倒数的符号相同,
即正数的倒数是正数,负数的倒数是负数.
(3)倒数是相互的,
(4)1或-1的倒数是它本身.
(5)求小数的倒数,要先把小数化成分数,
求带分数的倒数,要先把带分数化成假分数.
a≠0时,a的倒数是
例3
用正负数表示气温的变化量,上升为正,下降为负.
登山队攀登一座山峰,每登高1
km气温的变化量为-6℃,攀登3
km后,气温有什么变化?
解:(-6)×3=18(℃)
答:气温下降18℃.
随堂演练
被乘数
乘数
积的符号
积的绝对值
结果
-5
7
15
6
-1
-6
4
-25
1.填表:
-
35
-35
+
90
90
+
6
6
-
100
-100
2.
如图,数轴上A、B两点所表示的两个数的( )
?
A.和为正数 B.和为负数
C.积为正数
D.积为负数
D
3.
计算(-6)×(-1)的结果等于( )
A.6
B.-6
C.1
D.-1
A
4、-3的倒数是( )
A.3
B.
C.
D.-3
C
5.
计算:
(1)(-25)×(+4.8);
(2)
;
(3)0
×(-9.5);
(4)
.
解:(1)(-25)×(+4.8)=-(25
×
4.8)=-120;
(2)
;
(3)0
×(-9.5)=0;
(4)
.
6.气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少?
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
7.已知a的倒数是它本身,b是-10的相反数,负数c的绝对值是8,求式子4a-b+3c的值.
解:
因为a的倒数是它本身,所以a=±1.
因为b是-10的相反数,所以b=10.
因为负数c的绝对值是8,所以c=-8.
所以4a-b+3c=4×1-10+3×(-8)
=4-10+(-24)
=-30.
或4a-b+3c=4×(-1)-10+3×(-8)
=-4-10+(-24)
=-38.
如图,有甲乙两座水库,甲水库的水位每天升高3
cm
,乙水库的水位每天下降
3
cm
.
如果用“+”号表示水位的上升、用“?”号表示水位的下降,
请用算式表示,4
天后甲、乙水库水位的总变化量分别是多少?
甲水库
乙水库
3
cm
解:4
天后,甲水库水位的总变化量是:3×4=12cm
,即上升了12cm
乙水库水位的总变化量是:(?3)×4=-12cm
,即下降了12cm
课堂小结
有理数乘法
法则:
两数相乘,同号得正,异号得负,
并把绝对值相乘,
任何数同0相乘,都得0.
倒数:
乘积为1的两个数互为倒数.
https://www.21cnjy.com/help/help_extract.php
第一章
有理数
1.4.1
第1课时
有理数的乘法法则
随堂演练
课堂小结
获取新知
情景导入
例题讲解
知识回顾
知识回顾
计算:
(1)3+3+3+3;
(2)(-5)+(-5)+(-5);(3)(-5)×3
解:
(1)3+3+3+3=3×4=12;
(2)(-5)+(-5)+(-5)=-15;
(3)
(-5)×3
=?
.
如图,有甲乙两座水库,甲水库的水位每天升高3
cm
,乙水库的水位每天下降
3
cm
.
如果用“+”号表示水位的上升、用“?”号表示水位的下降,
请用算式表示,4
天后甲、乙水库水位的总变化量分别是多少?
甲水库
乙水库
3
cm
情景导入
获取新知
(1)a.观察下面的乘法算式,你能发现什么规律?
3×3=9,
3×2=6,
3×1=3,
3×0=0.
规律:
随着后一乘数逐次递减1,
.
积逐次递减3
b.
要使这个规律在引入负数后仍然成立,那么应有:
3×(-1)=
-3,
3×(-2)= ,
3×(-3)= .
-6
-9
c.
观察下面的算式,你又能发现什么规律?
3×3=9,
2×3=6,
1×3=3,
0×3=0.
随着前一乘数逐次递减1,积逐次递减3.
d.
要使c中的规律在引入负数后仍成立,那么应有:
(-1)×3= ,
(-2)×3= ,
(-3)×3= .
-3
-6
-9
归纳如下:
正数乘正数,积为正数;
正数乘负数,积是负数;
负数乘正数,积也是负数.
积的绝对值等于各个乘数绝对值的积.
(2)对于以上问题,以小组为单位进行观察总结归纳.你能得出正数乘正数、正数乘负数、负数乘正数的规律吗?
(3)利用(2)中结论计算下面的算式,你又发现了什么规律?
(-3)×3= ,
(-3)×2= ,
(-3)×1= ,
(-3)×0= .
-9
-6
-3
0
随着后一乘数逐次减1,积逐次增加3
(4)按照(3)中的规律,并总结归纳.
(-3)×(-1)= ,
(-3)×(-2)= ,
(-3)×(-3)= .
3
6
9
积为正数,乘积的绝对值等于各乘数绝对值的积.
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
讨论:
(1)若a<0,b>0,则ab
0
;
(2)若a<0,b<0,则ab
0
;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
例题讲解
(2)8×(-1)=-(8×1)=-8.
解:(1)(-3)×9=-(3×9)=-27.
(1)(-3)×9;(2)8×(-1);
例1
计算:
(3)(
)×(-2)=+(
×2
)=1.
从(2)中可以看出,
要得到一个数的相反数,只要将它乘-1
(3)中两个数的乘积是1,这样的两个数有什么特殊关系呢?
(3)(
)×(-2).
备注:
有理数乘法的求解步骤是
先确定积的符号
再确定积的绝对值
找特点,给这些数起一个你喜欢的名字.
1
1
1
认真观察每一对数,你发现了么?
两个乘数的分子
分母互相颠倒.
如果两个数的乘积是1,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数.
例2
求下列各数的倒数:
(1)
;(2)-1;(3)
;(4)0.125.
解:(1)
的倒数是
(2)-1
的倒数是-1
(3)
的倒数是
(4)0.125的倒数是8
要点精析:
(1)0没有倒数.
(2)一个数和它的倒数的符号相同,
即正数的倒数是正数,负数的倒数是负数.
(3)倒数是相互的,
(4)1或-1的倒数是它本身.
(5)求小数的倒数,要先把小数化成分数,
求带分数的倒数,要先把带分数化成假分数.
a≠0时,a的倒数是
例3
用正负数表示气温的变化量,上升为正,下降为负.
登山队攀登一座山峰,每登高1
km气温的变化量为-6℃,攀登3
km后,气温有什么变化?
解:(-6)×3=18(℃)
答:气温下降18℃.
随堂演练
被乘数
乘数
积的符号
积的绝对值
结果
-5
7
15
6
-1
-6
4
-25
1.填表:
-
35
-35
+
90
90
+
6
6
-
100
-100
2.
如图,数轴上A、B两点所表示的两个数的( )
?
A.和为正数 B.和为负数
C.积为正数
D.积为负数
D
3.
计算(-6)×(-1)的结果等于( )
A.6
B.-6
C.1
D.-1
A
4、-3的倒数是( )
A.3
B.
C.
D.-3
C
5.
计算:
(1)(-25)×(+4.8);
(2)
;
(3)0
×(-9.5);
(4)
.
解:(1)(-25)×(+4.8)=-(25
×
4.8)=-120;
(2)
;
(3)0
×(-9.5)=0;
(4)
.
6.气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少?
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
7.已知a的倒数是它本身,b是-10的相反数,负数c的绝对值是8,求式子4a-b+3c的值.
解:
因为a的倒数是它本身,所以a=±1.
因为b是-10的相反数,所以b=10.
因为负数c的绝对值是8,所以c=-8.
所以4a-b+3c=4×1-10+3×(-8)
=4-10+(-24)
=-30.
或4a-b+3c=4×(-1)-10+3×(-8)
=-4-10+(-24)
=-38.
如图,有甲乙两座水库,甲水库的水位每天升高3
cm
,乙水库的水位每天下降
3
cm
.
如果用“+”号表示水位的上升、用“?”号表示水位的下降,
请用算式表示,4
天后甲、乙水库水位的总变化量分别是多少?
甲水库
乙水库
3
cm
解:4
天后,甲水库水位的总变化量是:3×4=12cm
,即上升了12cm
乙水库水位的总变化量是:(?3)×4=-12cm
,即下降了12cm
课堂小结
有理数乘法
法则:
两数相乘,同号得正,异号得负,
并把绝对值相乘,
任何数同0相乘,都得0.
倒数:
乘积为1的两个数互为倒数.
https://www.21cnjy.com/help/help_extract.php
