【人教七上数学教学课件】1.5.1 第1课时 乘方的意义 课件(共22张PPT)
文档属性
| 名称 | 【人教七上数学教学课件】1.5.1 第1课时 乘方的意义 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 14:46:16 | ||
图片预览








文档简介
(共22张PPT)
第一章
有理数
1.5.1
第1课时
乘方的意义
随堂演练
课堂小结
获取新知
例题讲解
情景导入
情景导入
珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米.把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
获取新知
求下面正方形的面积与正方体的体积.
2cm
2×2=4(cm2)
2cm
2cm
2×2×2=8(cm3)
2×2,2×2×2都是相同因数的乘法.
为了方便,我们可以将它们记作什么,读作什么?
记作22,23
.
22读作“2的平方”(或“2的二次方”),
23
读作“2的立方”(或“2的三次方”).
(-2)×(-2)×(-2)
×(-2)记作什么?读作什么?
记作(-2)4,读作“-2的四次方”.
记作什么?读作什么?
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a·
·a
=
an
n个
…
乘方是一种特殊的乘法
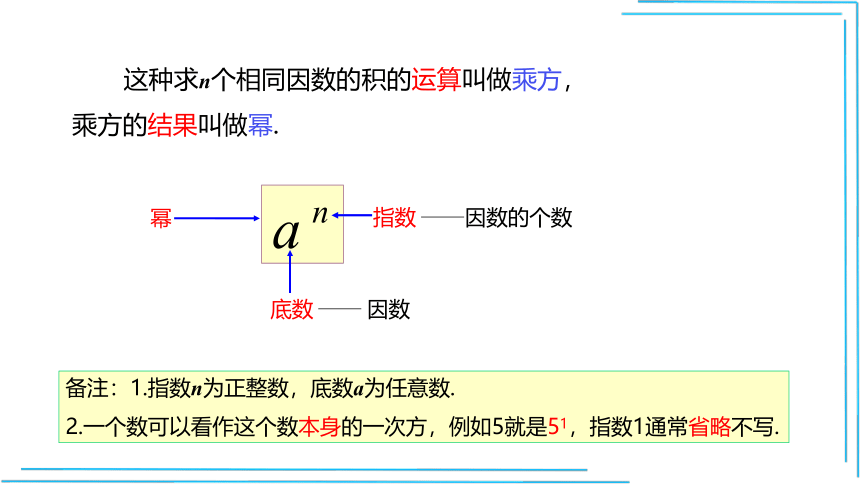
幂
指数
因数的个数
底数
因数
备注:1.指数n为正整数,底数a为任意数.
2.一个数可以看作这个数本身的一次方,例如5就是51,指数1通常省略不写.
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
例1
利用乘方的意义计算:
(3)
09=0.
?
思考:你发现正数的幂的正负有什么规律?0的幂呢?
解:(1)
53=5×5×5=125;
正数的任何次幂都是正数,0的任何正整数次幂都是0.
例题讲解
例2
计算:
(1)
(-4)3;
(2)
(-2)4;
(3)
解:(1)
(-4)3=(-4)×(-4)×(-4)=-64;
(2)
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
观察上述运算结果,你发现负数的幂的正负有什么规律?
负数的奇次幂是负数,负数的偶次幂是正数.
(1)
(2)
正数的任何次幂都是正数;
负数的
偶次幂是正数
奇次幂是负数
0的任何正整数次幂都是0
(3)
奇负偶正
幂的符号法则
例3
说说下列各数的意义,它们一样吗?
解:(-3)4底数是-3,指数是4
(-3)4的意义是4个-3相乘,结果是81
-34底数是3,指数是4
-34的意义是3的4次方的相反数,结果是-81
底数是
,指数是2,
意义是2个
相乘,结果是
底数是
2
,指数是2
,
意义是2的平方再除以3,结果是
(-3)4和-34
例4
用计算器计算(-8)5和(-3)6.
解:用带符号键
的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8)
5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3)
6
<
729.
所以(-8)5=-32768,(-3)6=729.
随堂演练
1.(-3)2计算的结果是( )
A.-6
B.6
C.-9
D.9
D
2.下列各数中,最小的是( )
A.-3
B.|-2|
C.(-3)2
D.2×103
A
3.下列等式成立的是( )
A.(-3)2=-32
B.-23=(-2)3
C.23=(-2)3
D.32=-32
D
4.-23表示的意义是(
)
A.(-2)×2×2
B.(-2)+(-2)+(-2)
C.(-2)×3
D.-2×2×2
B
5.(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2)
表示
个
相乘,读作
的
次方,也读作
的
次幂,其中
叫做
,6叫做
.
-5
2
-5
-5
平方
6
6
底数
指数
6
6.
计算(1)
(2)-23×(-32)
(3)64÷(-2)5
(4)(-4)3÷(-1)200+2×(-3)4
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
7.珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米.把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
解:折纸次数
纸的厚度(毫米)
1
0.1×2
2
0.1×2×2
3
0.1×2×2×2
…
30
0.1×2×2×···×2
=0.1×22
=0.1×23
30个2
=0.1×230
0.1×230=0.1×10
73741824毫米
=107374.1824米
>8848米
课堂小结
乘方的符号法则:
1.正数的任何次幂都是正数
2.负数的奇次幂是负数,负数的偶次幂是正数
3.零的正整数次幂都是零
幂
指数
底数
乘方
定义
求几个相同因数的积的运算
https://www.21cnjy.com/help/help_extract.php
第一章
有理数
1.5.1
第1课时
乘方的意义
随堂演练
课堂小结
获取新知
例题讲解
情景导入
情景导入
珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米.把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
获取新知
求下面正方形的面积与正方体的体积.
2cm
2×2=4(cm2)
2cm
2cm
2×2×2=8(cm3)
2×2,2×2×2都是相同因数的乘法.
为了方便,我们可以将它们记作什么,读作什么?
记作22,23
.
22读作“2的平方”(或“2的二次方”),
23
读作“2的立方”(或“2的三次方”).
(-2)×(-2)×(-2)
×(-2)记作什么?读作什么?
记作(-2)4,读作“-2的四次方”.
记作什么?读作什么?
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a·
·a
=
an
n个
…
乘方是一种特殊的乘法
幂
指数
因数的个数
底数
因数
备注:1.指数n为正整数,底数a为任意数.
2.一个数可以看作这个数本身的一次方,例如5就是51,指数1通常省略不写.
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
例1
利用乘方的意义计算:
(3)
09=0.
?
思考:你发现正数的幂的正负有什么规律?0的幂呢?
解:(1)
53=5×5×5=125;
正数的任何次幂都是正数,0的任何正整数次幂都是0.
例题讲解
例2
计算:
(1)
(-4)3;
(2)
(-2)4;
(3)
解:(1)
(-4)3=(-4)×(-4)×(-4)=-64;
(2)
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
观察上述运算结果,你发现负数的幂的正负有什么规律?
负数的奇次幂是负数,负数的偶次幂是正数.
(1)
(2)
正数的任何次幂都是正数;
负数的
偶次幂是正数
奇次幂是负数
0的任何正整数次幂都是0
(3)
奇负偶正
幂的符号法则
例3
说说下列各数的意义,它们一样吗?
解:(-3)4底数是-3,指数是4
(-3)4的意义是4个-3相乘,结果是81
-34底数是3,指数是4
-34的意义是3的4次方的相反数,结果是-81
底数是
,指数是2,
意义是2个
相乘,结果是
底数是
2
,指数是2
,
意义是2的平方再除以3,结果是
(-3)4和-34
例4
用计算器计算(-8)5和(-3)6.
解:用带符号键
的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8)
5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3)
6
<
729.
所以(-8)5=-32768,(-3)6=729.
随堂演练
1.(-3)2计算的结果是( )
A.-6
B.6
C.-9
D.9
D
2.下列各数中,最小的是( )
A.-3
B.|-2|
C.(-3)2
D.2×103
A
3.下列等式成立的是( )
A.(-3)2=-32
B.-23=(-2)3
C.23=(-2)3
D.32=-32
D
4.-23表示的意义是(
)
A.(-2)×2×2
B.(-2)+(-2)+(-2)
C.(-2)×3
D.-2×2×2
B
5.(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2)
表示
个
相乘,读作
的
次方,也读作
的
次幂,其中
叫做
,6叫做
.
-5
2
-5
-5
平方
6
6
底数
指数
6
6.
计算(1)
(2)-23×(-32)
(3)64÷(-2)5
(4)(-4)3÷(-1)200+2×(-3)4
(2)-23×(-32)=-8×(-9)=72;
(3)64÷(-2)5=64÷(-32)=-2;
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
7.珠穆朗玛峰是世界的最高峰,它的海拔高度是8844米.把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰,这是真的吗?
解:折纸次数
纸的厚度(毫米)
1
0.1×2
2
0.1×2×2
3
0.1×2×2×2
…
30
0.1×2×2×···×2
=0.1×22
=0.1×23
30个2
=0.1×230
0.1×230=0.1×10
73741824毫米
=107374.1824米
>8848米
课堂小结
乘方的符号法则:
1.正数的任何次幂都是正数
2.负数的奇次幂是负数,负数的偶次幂是正数
3.零的正整数次幂都是零
幂
指数
底数
乘方
定义
求几个相同因数的积的运算
https://www.21cnjy.com/help/help_extract.php
