第三章 机械波 4 波的干涉(64张PPT)
文档属性
| 名称 | 第三章 机械波 4 波的干涉(64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-12 18:17:08 | ||
图片预览











文档简介
(共64张PPT)
4 波的干涉
第三章 机械波
【学习目标】
1.理解波的叠加原理,知道干涉是波叠加的结果.
2.知道形成稳定干涉图样的条件.
梳理教材
夯实基础
探究重点
提升素养
随堂演练
逐点落实
课时
对点练
【内容索引】
SHULIJIAOCAI
HANGSHIJICHU
梳理教材 夯实基础
1
一、波的叠加
几列波相遇时能够保持各自的运动特征,继续传播,在它们重叠的区域里,介质的质点 参与这几列波引起的振动,质点的位移等于这几列波单独传播时引起的位移的 .
同时
矢量和
二、波的干涉
1.定义
相同、 恒定、 相同的两列波叠加时,某些区域的振动总是加强,某些区域的振动总是减弱,这种现象叫波的干涉.
2.干涉条件
(1)两列波的 必须相同.
(2)两个波源的 必须保持不变.
3.干涉的普遍性
一切波在一定条件下都能够发生干涉,干涉是 现象.
频率
相位差
振动方向
频率
相位差
波特有的
1.判断下列说法的正误.
(1)两列波相遇后各自的振动特点会受到影响.( )
(2)在两列波重叠的区域里,任何一个质点的位移都等于原来位移的2倍.
( )
(3)两列波叠加时,质点的位移一定增大.( )
(4)敲击音叉使其发声,然后转动音叉,听到声音忽强忽弱是声波的干涉现象.( )
(5)只有频率相同的两列波才可以叠加.( )
(6)在振动减弱的区域,各质点都处于波谷.( )
即学即用
×
×
×
√
×
×
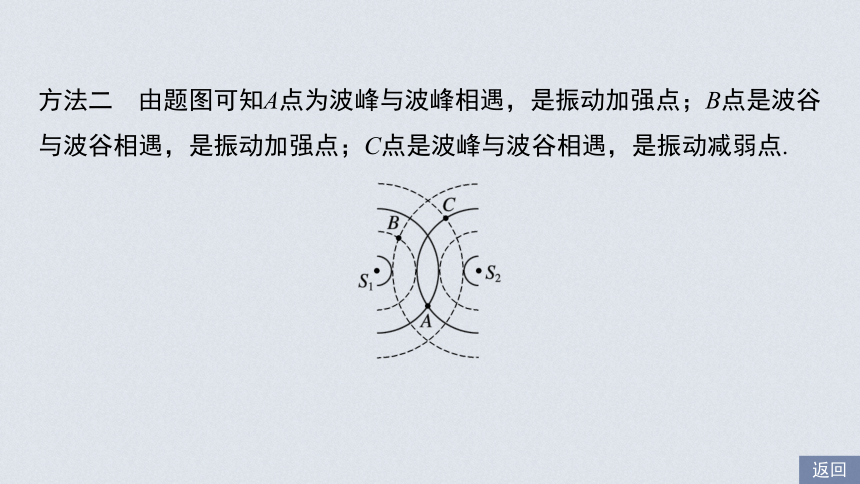
2.两个频率、振动方向、初始相位均相同的波源S1、S2,产生的波在同一介质中传播时,某时刻t形成如图1所示的干涉图样,图样中两波源S1、S2同时为波谷(实线表示波峰,虚线表示波谷),在图中标有A、B、C三个点,则振动加强的点是______,振动减弱的点是____.
图1
A、B
C
解析 方法一 由题图可以知道,A点到波源S1、S2的距离均为1.5λ,即x1=1.5λ,x2=1.5λ,故A到S1、S2的距离差Δx=x1-x2=0;B点到S1的距离为x1=λ,到S2的距离为x2=2λ,故B到S1、S2的距离差Δx=λ;C点到S1的距离为x1=2λ,到S2的距离为x2=1.5λ,故C到两波源S1、S2的距离差为Δx=x1-x2=0.5λ.因为两波源的振动情况完全相同,所以A、B点处振动情况相同,C点处振动情况相反,故A、B点均为振动加强点,C点为振动减弱点.
方法二 由题图可知A点为波峰与波峰相遇,是振动加强点;B点是波谷与波谷相遇,是振动加强点;C点是波峰与波谷相遇,是振动减弱点.
返回
TANJIUZHONGDIAN
TISHENGSUYANG
探究重点 提升素养
2
一、波的叠加
(1)两个同学分别抓住绳子的两端,各自抖动一下,绳上产生两列凸起且相向传播的波,两列波相遇后是否还保持原来的运动状态继续传播?
答案 两列波相遇后仍然保持原来各自的运动状态继续传播,并没有受到另一列波的影响
(2)当教室内乐队合奏时,我们听到的某种乐器的声音与这种乐器独奏时发出的声音是否相同?这种声音是否受到了其他乐器的影响?
答案 相同,没有受到其他乐器的影响
导学探究
1.波的独立传播特性:几列波相遇时各自的波长、频率等运动特征,不受其他波的影响.
2.波的叠加原理:在几列波重叠的区域里,介质的质点同时参与这几列波引起的振动,质点的位移等于这几列波单独传播时引起的位移的矢量和.
知识深化
例1 如图2所示,波源S1在绳的左端发出频率为f1、振幅为A1的半个波形a,同时另一个波源S2在绳的右端发出频率为f2、振幅为A2的半个波形b,且f1A.两列波比较,a波将先到达P点
B.两列波在P点叠加时,P点的位移最大可达A1+A2
C.a、b的波峰同时到达P点
D.两列波相遇时,绳上位移可达A1+A2的点只有一个,此点在P点的左侧
√
图2
解析 因两列波波速相等,故两列波能同时到达P点,A错误;
因f1可知,λ1>λ2,故当两列波同时到达P点
时,a波的波峰离P点的距离比b波的波峰离P点的距离大,因此两波峰不能同时到达P点,两波峰应相遇在P点左侧,此位置对应的位移为A1+A2,位移最大,综上所述,B、C错误,D正确.
针对训练1 (2020·上海建平中学月考)如图3甲,两列振幅和波长相同而传播方向相反的波,在相遇的某一时刻(如图乙),两列波“消失”,此时介质中M、N两质点的运动方向是
A.M、N都静止
B.M、N都向上
C.M向下,N向上
D.M向上,N向下
√
图3
解析 由题图可知,两列波的波峰与波谷叠加,振动减弱,两波的振幅相等,所以题图乙所示的时刻两列波“消失”.根据波形平移法判断可知,向右传播的波单独引起M的运动方向向下,N的运动方向向上,向左传播的波单独引起M的运动方向向下,N的运动方向向上,根据波的叠加原理可知,此时M质点的运动方向向下,N质点的运动方向向上,故C正确,A、B、D错误.
二、波的干涉
如图4所示,与振动发生器相连的两个小球,在振动发生器的带动下上下振动,形成两个振动频率和振动步调相同的波源,在水面上形成两列步调、频率相同的波,两列波在水面上相遇时,能观察到什么现象?如果改变其中一个小球振动的快慢,还会形成这种现象吗?
导学探究
图4
答案 在水面上出现一条条从两个波源中间伸展开的相对平静的区域和剧烈振动的区域.改变其中一个小球振动的快慢,这种现象将消失
1.发生干涉的条件:(1)两列波的频率相同;(2)相位差恒定;(3)振动方向相同.
2.产生稳定干涉图样的两列波的振幅越接近,干涉图样越明显.
3.干涉图样及其特点
(1)干涉图样:如图5所示.
知识深化
图5
(2)特点
①加强区始终加强,减弱区始终减弱(加强区与减弱区不随时间变化).
②加强区和减弱区的位置固定不变,加强区与减弱区互相间隔.
③加强点的振幅为A1+A2;减弱点的振幅为|A1-A2|,每个质点都在各自的平衡位置附近做简谐运动.
例2 如图6所示,S1、S2是两个步调完全相同的相干波源,其中实线表示波峰,虚线表示波谷.若两列波的振幅均保持5
cm不变,关于图中所标的b、c、d三点,下列说法正确的是
A.d点始终保持静止不动
B.图示时刻c点的位移为零
C.b点振动始终加强,c点振动始终减弱
D.图示时刻,b、c两点的竖直高度差为10
cm
命题角度1 波的干涉的分析
图6
√
解析 d点是波峰与波谷相遇,振动减弱,振幅为零,故保持静止,故A正确;
b点是波峰与波峰相遇,c点是波谷与波谷相遇,它们均属于振动加强点,由于振幅是5
cm,则b点相对平衡位置高10
cm,c点相对平衡位置低10
cm,所以b、c两点的竖直高度差为20
cm,故B、C、D错误.
针对训练2 两列完全相同的机械波于某时刻的叠加情况如图7所示,图中的实线和虚线分别表示波峰和波谷,此时
A.a、b连线中点振动减弱
B.a、b、c、d四点速度均为零
C.再经过
周期,c、d两点振动加强
D.再经过
周期,c、d两点振动加强
图7
√
解析 题图中a点处波谷与波谷相遇,b点处波峰与波峰相遇,两点速度均为零,a、b连线上的点均为振动加强点,振动始终加强;c、d两点振动始终减弱,振幅为0,即质点静止,B正确.
例3 如图8(a),在xy平面内有两个沿z方向做简谐振动的点波源S1(0,4)和S2(0,-2).两波源的振动图线分别如图(b)和图(c)所示.两列波的波速均为1.00
m/s.两列波从波源传播到点A(8,-2)的路程差为____m,两列波引起的点B(4,1)处质点的振动相互_____(填“加强”或“减弱”),点C(0,0.5)处质点的振动相互_____(填“加强”或“减弱”).
命题角度2 加强点、减弱点的判断
图8
2
减弱
加强
解析 由几何关系可知两波源到A点的距离为AS1=10
m,AS2=8
m,所以两波源到A点的路程差为2
m;同理可得,BS1-BS2=0,为波长的整数倍,由振动图像知两振源振动方向相反,故B点振动减弱;两波源到C点的路程差为Δx=CS1-CS2=1
m,波长λ=vT=2
m,所以C点振动加强.
振动加强点和减弱点的判断方法
1.条件判断法:频率相同、振动情况完全相同的两波源产生的波叠加时,加强、减弱条件如下:设点到两波源的距离差为Δr,则当Δr=kλ时为加强点,当Δr=(2k+1)
时为减弱点,其中k=0,1,2….若两波源振动步调相反,则上述结论相反.
2.现象判断法:若某点处总是波峰与波峰(或波谷与波谷)相遇,该点为加强点;若总是波峰与波谷相遇,则为减弱点;若某点处是平衡位置和平衡位置相遇,则让两列波再传播
T,看该点是波峰和波峰(波谷和波谷)相遇,还是波峰和波谷相遇,从而判断该点是加强点还是减弱点.
总结提升
返回
SUITANGYANLIAN
ZHUDIANLUOSHI
随堂演练 逐点落实
3
1.(波的叠加)如图9所示为两列相向传播的、振幅和波长都相同的横波,它们在O点相遇,此后可能出现的状态是
1
2
3
4
图9
√
2.(波的干涉)如图10所示,S1、S2是两个相干波源,它们的相位及振幅均相同.实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷.关于图中所标的a、b、c三点,下列说法正确的是
1
2
3
4
A.a质点振动减弱,b、c质点振动加强
B.a质点振动加强,b、c质点振动减弱
C.再过
后,b、c两质点都将处于各自的平衡
位置,振动将减弱
D.a点一直在平衡位置,b点一直在波峰,c点一直在波谷
√
图10
解析 a质点处是两列波波峰与波谷叠加的地方,振动始终减弱,而b、c质点处是两列波波峰与波峰、波谷与波谷叠加的地方,振动始终加强,故A对,B、C错;
1
2
3
4
因为两个波源的振动方向相同、振幅相同,所以a点静止不动,一直在平衡位置,b、c两点的振动始终是加强的,但它们仍在振动,位移随时间周期性变化,不是静止不动的,故D错.
3.(波的干涉)如图11所示为甲、乙两列简谐横波在同一绳上传播时某时刻的波形图,甲波向右传播,乙波向左传播.质点M位于x=0.2
m处,则下列说法正确的是
1
2
3
4
A.这两列波不会发生干涉现象
B.质点M的振动总是加强
C.质点M将做振幅为10
cm的简谐振动
D.由图示时刻开始,再经过 甲波周期,质点
M将位于波峰
图11
√
1
2
3
4
解析 两列简谐横波在同一均匀介质内传播,波速相等,由题图可知两列波的波长相等,由v=λf可知,频率相等,所以两列波能发生干涉现象,故A错误;
x=0.2
m处是振动加强点,振动总是加强,振幅等于两列波振幅之和,为A=20
cm+10
cm=30
cm,则质点M将做振幅为30
cm的简谐振动,故B正确,C错误;
从题图所示时刻开始,再经过 甲波周期,质点M将位于波谷,故D错误.
4.(波的干涉)如图12所示,在直线PQ的垂线OM上有A、B两个声源,A、B分别距O点6
m和1
m,两个声源同时不断向外发出波长都为2
m的完全相同的声波,在直线PQ上从-∞到+∞的范围内听不到声音的区域共有多少个?
1
2
3
4
图12
答案 5个
解析 若某点到两波源的路程差为波长的整数倍,即Δx=nλ(n=0,1,2…),则该点振动加强,
1
2
3
4
返回
若某点到两波源的路程差为半波长的奇数倍,即Δx=
(2n+1)(n=0,1,2…),则该点振动减弱.
直线PQ上的O点距两波源A、B的路程差最大,即AO-BO=(6-1)
m=
5
m=
λ,
故O点为减弱点,由O向-∞或由O向+∞,直线PQ上各点到两波源A、B的路程差逐渐减小,
所以在直线PQ上从-∞到+∞的范围内听不到声音的区域共有5个.
KE
SHI
DUI
DIAN
LIAN
课时对点练
4
考点一 波的叠加
1.两列波在某区域相遇,下列说法正确的是
A.两列波相遇时运动状态互相干扰
B.由于这两列波相遇时叠加,当它们分开时波的频率、振幅都会发生变化
C.这两列波叠加以后一定会产生干涉图样
D.两列波重叠的区域里,任何一点的总位移都等于两列波分别引起的位
移的矢量和
基础对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 由波的独立传播特性和波的叠加原理可知,选项D正确,A、B错误;
只有频率相同、相位差恒定的两列波叠加后才能发生干涉现象,产生干涉图样,选项C错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
2.关于波的叠加和干涉,下列说法正确的是
A.两列频率不相同的波相遇时,因为没有稳定的干涉图样,所以波没有
叠加
B.两列频率相同的波相遇时,振动加强的点只是波峰与波峰相遇的点
C.两列频率相同的波相遇时,介质中振动加强的质点在某时刻的位移可
能是零
D.两列频率相同的波相遇时,振动加强的质点的位移总是比振动减弱的
质点的位移大
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 两列波相遇时一定叠加,没有条件,A错误;
振动加强是指振幅增大,而不只是波峰与波峰相遇,B错误;
振动加强点的振幅增大,质点仍然在自己的平衡位置附近振动,故某时刻的位移可以是振幅范围内的任何值,C正确,D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
3.(2020·河北冀州中学期中)一条弹性绳子呈水平状态.M为绳子中点(图中未画出),两端P、Q同时开始上下振动,一小段时间后产生的波形如图1所示.对于其后绳上各点的振动情况,以下判断正确的是
A.两列波将同时到达中点M
B.两列波波速之比为1∶2
C.中点M的振动总是加强的
D.M点的位移大小不可能为零
1
2
3
4
5
6
7
8
9
10
11
12
13
图1
√
解析 波在同种介质中传播,波速相同,由于M为绳子中点,所以两波同时到达M点,故A正确,B错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
由于波长不同,因此两波在M点相遇时,M点的振动并不总是加强或减弱,故C错误;
当两波刚传到M点时,此时刻位移为零,所以M点的位移大小在某时刻可能为零,故D错误.
考点二 波的干涉
4.(2020·济南市期末)内燃机、通风机等在排放各种高速气流的过程中都会发出噪声,如图2所示为某种消声器的示意图,可以用来削弱高速气流产生的噪声.一列声波沿水平管道自左向右传播,到达a处时分成上下两束波,这两束声波在b处相遇时可削弱噪声.关于此消声器,下列说法正确的是
A.利用了波的反射原理
B.利用了波的衍射原理
C.只能消除某一频率的噪声
D.可以消除某些频率的噪声
1
2
3
4
5
6
7
8
9
10
11
12
13
图2
√
5.两列振动方向相同、振幅分别为A1和A2的相干简谐横波相遇.下列说法正确的是
A.波峰与波谷相遇处质点的振幅为0
B.波峰与波峰相遇处质点离开平衡位置的位移始终为A1+A2
C.波峰与波谷相遇处质点的位移总是小于波峰与波峰相遇处质点的位移
D.波峰与波峰相遇处质点的振幅一定大于波峰与波谷相遇处质点的振幅
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 波峰与波谷相遇处质点的实际振幅为|A1-A2|,故选项A错误;
波峰与波峰相遇处,质点的振幅最大,合振幅为A1+A2,但此处质点仍处于振动状态,其位移随时间按正弦规律变化,故选项B错误;
振动减弱点和振动加强点的位移均随时间按正弦规律变化,故选项C错误;
波峰与波峰相遇时振动加强,波峰与波谷相遇时振动减弱,振动加强点的振幅大于振动减弱点的振幅,故选项D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
6.(2020·临沂市期末)如图3所示,两个相干波源S1、S2产生的波在同一种均匀介质中相遇.图中实线表示某时刻的波峰,虚线表示的是波谷,下列说法正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
A.a点的振动加强,b、c、d点的振动减弱
B.e、f两点的振动介于加强和减弱之间
C.经适当的时间后,加强点和减弱点的位置互换
D.经半个周期后,原来位于波峰的点将位于波谷,原来位于波谷的点将
位于波峰
图3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 a点是波谷和波谷相遇的点,c点是波峰和波峰相遇的点,都是振动加强点;而b、d两点都是波峰和波谷相遇的点,是振动减弱点,A错误.
e点位于加强点的连线上,为加强点;f点位于减弱点的连线上,为减弱点,B错误.
相干波源产生的波的干涉是稳定的,加强点与减弱点不会随时间变化,C错误.
因形成干涉图样的质点也在不停地做周期性振动,经半个周期原来位于波峰的点将位于波谷,原来位于波谷的点将位于波峰,D正确.
7.在学校运动场上50
m直跑道的两端,分别安装了由同一信号发生器带动的两个相同的扬声器.两个扬声器连续发出波长为5
m的声波.一同学从该跑道的中点出发,向某一端点缓慢行进10
m.在此过程中,他听到扬声器声音由强变弱的次数为
A.2
B.4
C.6
D.8
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 根据波的干涉的加强点和减弱点的条件,可知当某点与两个波源距离差为波长的整数倍时,该点为振动加强点,即声音加强点,由题意可知,Δx=nλ=5n(n=0,1,2…),所以这位同学距离跑道两端相差5
m的整数倍时,即这位同学每向前运动2.5
m,就为一个声音加强点,10
m内共有5个加强点(包括两端),则由强变弱的次数为4次,故选B.
8.(2020·威海市期末)固定在同一个振动片上的两根细杆,当振动片振动时,两根细杆周期性地触动水面,形成两个波源.两列波相遇后,形成稳定的干涉图样,图4仅为示意图.已知两波源间的距离为0.6
m,波长为0.25
m,下列判断正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
A.两波源的频率相同,相位差恒定
B.振动加强区域各质点的振动频率为波源的2倍
C.在水面上放一树叶,树叶会振动着向水槽边缘飘去
D.两波源的连线上振动加强的位置有4处
图4
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 能形成稳定的干涉图样,两列波必须频率相同,相位差恒定,A正确,B错误;
树叶会上、下振动,但不会沿波的传播方向移动,故C错误;
设s1、s2为两波源连线上某点到两波源的距离,两波源连线上的加强点应满足|s1-s2|=nλ(n=0,1,2,3…),n可能的取值为0、1、2,所以两波源连线上振动加强的位置有5处,D错误.
9.如图5所示为t=0时刻简谐横波a与b的波形图,其中a沿x轴正方向传播,b沿x轴负方向传播,波速都是10
m/s,振动方向都平行于y轴.下列选项画出的是平衡位置在x=2
m处的质点从t=0开始在一个周期内的振动图像,其中正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
能力提升练
图5
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 由题可知,两列波的波速相等,波长相等,则频率相等,能发生干涉.过 周期后,两列波的波峰同时到达x=2
m处的质点,则此质点振动总是加强,振幅为两列波振幅之和,即为3
cm,t=0时刻该质点从平衡位置沿y轴正方向运动,所以B正确.
10.(2020·聊城市二模)如图6所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-1.0
m和x=5.0
m处,两列波的速率均为v=2
m/s,两波源的振幅均为A=2
cm.图示为t=0时刻两列波的图像(传播方向如图所示),此刻平衡位置处于x=1.0
m和x=3.0
m的M、N两质点刚开始振动.质点P、Q的平衡位置分别处于x=2.0
m和x=2.5
m处,关于各质点运动情况判断正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
A.质点Q的起振方向沿y轴负方向
B.t=1.25
s时刻,质点M的位移为-4
cm
C.两列波能发生干涉,发生干涉后质点P处
为振动减弱点
D.两列波能发生干涉,发生干涉后质点Q处为振动减弱点
图6
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 M、N刚开始振动,由同侧法可知,质点M向下振动,质点N向上振动,即两列波的起振方向相反.由于两列波的传播速度相等,Q距N近,故质点N的振动形式先传播到质点Q,故质点Q的起振方向与质点N的起振方向相同,起振时沿y轴正方向,A错误;
质点M的平衡位置距两波源的距离差值为一个波长,因两列波的起振方向相反,故质点M处为振动减弱点,两列波的振幅相同,故质点M的位移始终为零,B错误;
同理可判断质点P处为振动减弱点,质点Q处为振动加强点,C正确,D错误.
11.(2021·天津市静海一中高二月考)如图7甲所示,两个相干波源S1、S2产生的波在同一均匀介质中相遇.图中实线表示波峰,虚线表示波谷,c和f分别为ae和bd的中点,则:
1
2
3
4
5
6
7
8
9
10
11
12
13
图7
(1)在a、b、c、d、e、f六点中,振动加强的点是________,振动减弱的点是________.
a、c、e
b、d、f
解析 由题图甲可知,a点是波谷与波谷相遇点,而b、d点是波峰与波谷相遇点,e点是波峰与波峰相遇点.由于当波峰与波峰相遇或波谷与波谷相遇时振动加强,当波峰与波谷相遇时振动减弱,所以a、e是振动加强点,b、d是振动减弱点;在波的传播方向上,振动加强点的连线上也是振动加强点,振动减弱点的连线上也是振动减弱点;c在振动加强点的连线上,f在振动减弱点的连线上,因此c是振动加强点,而f是振动减弱点.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)若两振源S1和S2振幅不相同,此时位移为零的点是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 若两振源S1和S2振幅不相同,波峰与波谷相遇处点的位移不为零,平衡位置相遇处点的位移为零,此时刻位移为零的点是c、f.
c、f
(3)在图乙中画出此时刻ace连线上,以a为原点的一列完整波形,标出a、c、e点.
1
2
3
4
5
6
7
8
9
10
11
12
13
答案 如图所示
12.如图8所示,S1、S2是两个同向的相干波源,相距4
m,两列相干波的波长均为λ=2
m,则在以S1、S2连线为半径、S2为圆心的圆周上共有几处振动减弱的点?
1
2
3
4
5
6
7
8
9
10
11
12
13
图8
答案 8
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 两列相干波在空间上会发生稳定的干涉现象,其振动加强或减弱由两列波波源到该点的距离差及波长决定:
当距离差Δx=nλ(n=0,1,2…)时,振动加强;当Δx=(2n+1)
(n=0,1,2…)时,振动减弱.
设圆周上某点P振动减弱.如图所示,
由干涉条件得:
|S1P-S2P|=(2n+1)
(n=0,1,2,…)
而λ=2
m,S2P=4
m,S1P:0~8
m,分别代入后可得共有8处振动减弱的点(注意是整个圆周上).
13.(2020·上海市期中)“华附讲坛”是华师附中邀请专家做前沿专题报告的常规学术活动,通常在东阶梯课室举办.图9是课室主席台的平面图,AB是讲台,S1、S2是与讲台上话筒等高的相同的喇叭,它们相互之间的位置和尺寸如图所示.专家的声音放大后经喇叭传回话筒再次放大时可能会产生啸叫.为了避免啸叫,话筒最好摆放在讲台上适当的位置,在这些
1
2
3
4
5
6
7
8
9
10
11
12
13
尖子生选练
位置上两个喇叭传来的声音因干涉而相消.已知空气中声速为v=340
m/s,专家声音的频率为f=136
Hz,忽略讲台的宽度,则:
图9
(1)求专家声音的波长λ;
答案 2.5
m
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 专家声音的波长是λ=
=2.5
m.
(2)图中B点是振动加强点还是振动减弱点,试通过计算说明判断依据;
答案 见解析
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 B点与两个声源的路程差为ΔxB=
=5
m=2λ.
即两个声源到B点的距离差为波长的整数倍,
所以B点为振动加强点.
(3)讲台上能够避免啸叫的适当位置有多少个?
答案 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 设P是AB上任意的一个消音点,
则该点与两个声源的路程差应该满足ΔxP=
=±(2k+1)
(k=
0,1,2,3…),
由于P是在AB间的点,即有|ΔxP|<2λ
因此k只能取0和1,因此AB上共有4个消音点.
返回
本课结束
4 波的干涉
第三章 机械波
【学习目标】
1.理解波的叠加原理,知道干涉是波叠加的结果.
2.知道形成稳定干涉图样的条件.
梳理教材
夯实基础
探究重点
提升素养
随堂演练
逐点落实
课时
对点练
【内容索引】
SHULIJIAOCAI
HANGSHIJICHU
梳理教材 夯实基础
1
一、波的叠加
几列波相遇时能够保持各自的运动特征,继续传播,在它们重叠的区域里,介质的质点 参与这几列波引起的振动,质点的位移等于这几列波单独传播时引起的位移的 .
同时
矢量和
二、波的干涉
1.定义
相同、 恒定、 相同的两列波叠加时,某些区域的振动总是加强,某些区域的振动总是减弱,这种现象叫波的干涉.
2.干涉条件
(1)两列波的 必须相同.
(2)两个波源的 必须保持不变.
3.干涉的普遍性
一切波在一定条件下都能够发生干涉,干涉是 现象.
频率
相位差
振动方向
频率
相位差
波特有的
1.判断下列说法的正误.
(1)两列波相遇后各自的振动特点会受到影响.( )
(2)在两列波重叠的区域里,任何一个质点的位移都等于原来位移的2倍.
( )
(3)两列波叠加时,质点的位移一定增大.( )
(4)敲击音叉使其发声,然后转动音叉,听到声音忽强忽弱是声波的干涉现象.( )
(5)只有频率相同的两列波才可以叠加.( )
(6)在振动减弱的区域,各质点都处于波谷.( )
即学即用
×
×
×
√
×
×
2.两个频率、振动方向、初始相位均相同的波源S1、S2,产生的波在同一介质中传播时,某时刻t形成如图1所示的干涉图样,图样中两波源S1、S2同时为波谷(实线表示波峰,虚线表示波谷),在图中标有A、B、C三个点,则振动加强的点是______,振动减弱的点是____.
图1
A、B
C
解析 方法一 由题图可以知道,A点到波源S1、S2的距离均为1.5λ,即x1=1.5λ,x2=1.5λ,故A到S1、S2的距离差Δx=x1-x2=0;B点到S1的距离为x1=λ,到S2的距离为x2=2λ,故B到S1、S2的距离差Δx=λ;C点到S1的距离为x1=2λ,到S2的距离为x2=1.5λ,故C到两波源S1、S2的距离差为Δx=x1-x2=0.5λ.因为两波源的振动情况完全相同,所以A、B点处振动情况相同,C点处振动情况相反,故A、B点均为振动加强点,C点为振动减弱点.
方法二 由题图可知A点为波峰与波峰相遇,是振动加强点;B点是波谷与波谷相遇,是振动加强点;C点是波峰与波谷相遇,是振动减弱点.
返回
TANJIUZHONGDIAN
TISHENGSUYANG
探究重点 提升素养
2
一、波的叠加
(1)两个同学分别抓住绳子的两端,各自抖动一下,绳上产生两列凸起且相向传播的波,两列波相遇后是否还保持原来的运动状态继续传播?
答案 两列波相遇后仍然保持原来各自的运动状态继续传播,并没有受到另一列波的影响
(2)当教室内乐队合奏时,我们听到的某种乐器的声音与这种乐器独奏时发出的声音是否相同?这种声音是否受到了其他乐器的影响?
答案 相同,没有受到其他乐器的影响
导学探究
1.波的独立传播特性:几列波相遇时各自的波长、频率等运动特征,不受其他波的影响.
2.波的叠加原理:在几列波重叠的区域里,介质的质点同时参与这几列波引起的振动,质点的位移等于这几列波单独传播时引起的位移的矢量和.
知识深化
例1 如图2所示,波源S1在绳的左端发出频率为f1、振幅为A1的半个波形a,同时另一个波源S2在绳的右端发出频率为f2、振幅为A2的半个波形b,且f1
B.两列波在P点叠加时,P点的位移最大可达A1+A2
C.a、b的波峰同时到达P点
D.两列波相遇时,绳上位移可达A1+A2的点只有一个,此点在P点的左侧
√
图2
解析 因两列波波速相等,故两列波能同时到达P点,A错误;
因f1
时,a波的波峰离P点的距离比b波的波峰离P点的距离大,因此两波峰不能同时到达P点,两波峰应相遇在P点左侧,此位置对应的位移为A1+A2,位移最大,综上所述,B、C错误,D正确.
针对训练1 (2020·上海建平中学月考)如图3甲,两列振幅和波长相同而传播方向相反的波,在相遇的某一时刻(如图乙),两列波“消失”,此时介质中M、N两质点的运动方向是
A.M、N都静止
B.M、N都向上
C.M向下,N向上
D.M向上,N向下
√
图3
解析 由题图可知,两列波的波峰与波谷叠加,振动减弱,两波的振幅相等,所以题图乙所示的时刻两列波“消失”.根据波形平移法判断可知,向右传播的波单独引起M的运动方向向下,N的运动方向向上,向左传播的波单独引起M的运动方向向下,N的运动方向向上,根据波的叠加原理可知,此时M质点的运动方向向下,N质点的运动方向向上,故C正确,A、B、D错误.
二、波的干涉
如图4所示,与振动发生器相连的两个小球,在振动发生器的带动下上下振动,形成两个振动频率和振动步调相同的波源,在水面上形成两列步调、频率相同的波,两列波在水面上相遇时,能观察到什么现象?如果改变其中一个小球振动的快慢,还会形成这种现象吗?
导学探究
图4
答案 在水面上出现一条条从两个波源中间伸展开的相对平静的区域和剧烈振动的区域.改变其中一个小球振动的快慢,这种现象将消失
1.发生干涉的条件:(1)两列波的频率相同;(2)相位差恒定;(3)振动方向相同.
2.产生稳定干涉图样的两列波的振幅越接近,干涉图样越明显.
3.干涉图样及其特点
(1)干涉图样:如图5所示.
知识深化
图5
(2)特点
①加强区始终加强,减弱区始终减弱(加强区与减弱区不随时间变化).
②加强区和减弱区的位置固定不变,加强区与减弱区互相间隔.
③加强点的振幅为A1+A2;减弱点的振幅为|A1-A2|,每个质点都在各自的平衡位置附近做简谐运动.
例2 如图6所示,S1、S2是两个步调完全相同的相干波源,其中实线表示波峰,虚线表示波谷.若两列波的振幅均保持5
cm不变,关于图中所标的b、c、d三点,下列说法正确的是
A.d点始终保持静止不动
B.图示时刻c点的位移为零
C.b点振动始终加强,c点振动始终减弱
D.图示时刻,b、c两点的竖直高度差为10
cm
命题角度1 波的干涉的分析
图6
√
解析 d点是波峰与波谷相遇,振动减弱,振幅为零,故保持静止,故A正确;
b点是波峰与波峰相遇,c点是波谷与波谷相遇,它们均属于振动加强点,由于振幅是5
cm,则b点相对平衡位置高10
cm,c点相对平衡位置低10
cm,所以b、c两点的竖直高度差为20
cm,故B、C、D错误.
针对训练2 两列完全相同的机械波于某时刻的叠加情况如图7所示,图中的实线和虚线分别表示波峰和波谷,此时
A.a、b连线中点振动减弱
B.a、b、c、d四点速度均为零
C.再经过
周期,c、d两点振动加强
D.再经过
周期,c、d两点振动加强
图7
√
解析 题图中a点处波谷与波谷相遇,b点处波峰与波峰相遇,两点速度均为零,a、b连线上的点均为振动加强点,振动始终加强;c、d两点振动始终减弱,振幅为0,即质点静止,B正确.
例3 如图8(a),在xy平面内有两个沿z方向做简谐振动的点波源S1(0,4)和S2(0,-2).两波源的振动图线分别如图(b)和图(c)所示.两列波的波速均为1.00
m/s.两列波从波源传播到点A(8,-2)的路程差为____m,两列波引起的点B(4,1)处质点的振动相互_____(填“加强”或“减弱”),点C(0,0.5)处质点的振动相互_____(填“加强”或“减弱”).
命题角度2 加强点、减弱点的判断
图8
2
减弱
加强
解析 由几何关系可知两波源到A点的距离为AS1=10
m,AS2=8
m,所以两波源到A点的路程差为2
m;同理可得,BS1-BS2=0,为波长的整数倍,由振动图像知两振源振动方向相反,故B点振动减弱;两波源到C点的路程差为Δx=CS1-CS2=1
m,波长λ=vT=2
m,所以C点振动加强.
振动加强点和减弱点的判断方法
1.条件判断法:频率相同、振动情况完全相同的两波源产生的波叠加时,加强、减弱条件如下:设点到两波源的距离差为Δr,则当Δr=kλ时为加强点,当Δr=(2k+1)
时为减弱点,其中k=0,1,2….若两波源振动步调相反,则上述结论相反.
2.现象判断法:若某点处总是波峰与波峰(或波谷与波谷)相遇,该点为加强点;若总是波峰与波谷相遇,则为减弱点;若某点处是平衡位置和平衡位置相遇,则让两列波再传播
T,看该点是波峰和波峰(波谷和波谷)相遇,还是波峰和波谷相遇,从而判断该点是加强点还是减弱点.
总结提升
返回
SUITANGYANLIAN
ZHUDIANLUOSHI
随堂演练 逐点落实
3
1.(波的叠加)如图9所示为两列相向传播的、振幅和波长都相同的横波,它们在O点相遇,此后可能出现的状态是
1
2
3
4
图9
√
2.(波的干涉)如图10所示,S1、S2是两个相干波源,它们的相位及振幅均相同.实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷.关于图中所标的a、b、c三点,下列说法正确的是
1
2
3
4
A.a质点振动减弱,b、c质点振动加强
B.a质点振动加强,b、c质点振动减弱
C.再过
后,b、c两质点都将处于各自的平衡
位置,振动将减弱
D.a点一直在平衡位置,b点一直在波峰,c点一直在波谷
√
图10
解析 a质点处是两列波波峰与波谷叠加的地方,振动始终减弱,而b、c质点处是两列波波峰与波峰、波谷与波谷叠加的地方,振动始终加强,故A对,B、C错;
1
2
3
4
因为两个波源的振动方向相同、振幅相同,所以a点静止不动,一直在平衡位置,b、c两点的振动始终是加强的,但它们仍在振动,位移随时间周期性变化,不是静止不动的,故D错.
3.(波的干涉)如图11所示为甲、乙两列简谐横波在同一绳上传播时某时刻的波形图,甲波向右传播,乙波向左传播.质点M位于x=0.2
m处,则下列说法正确的是
1
2
3
4
A.这两列波不会发生干涉现象
B.质点M的振动总是加强
C.质点M将做振幅为10
cm的简谐振动
D.由图示时刻开始,再经过 甲波周期,质点
M将位于波峰
图11
√
1
2
3
4
解析 两列简谐横波在同一均匀介质内传播,波速相等,由题图可知两列波的波长相等,由v=λf可知,频率相等,所以两列波能发生干涉现象,故A错误;
x=0.2
m处是振动加强点,振动总是加强,振幅等于两列波振幅之和,为A=20
cm+10
cm=30
cm,则质点M将做振幅为30
cm的简谐振动,故B正确,C错误;
从题图所示时刻开始,再经过 甲波周期,质点M将位于波谷,故D错误.
4.(波的干涉)如图12所示,在直线PQ的垂线OM上有A、B两个声源,A、B分别距O点6
m和1
m,两个声源同时不断向外发出波长都为2
m的完全相同的声波,在直线PQ上从-∞到+∞的范围内听不到声音的区域共有多少个?
1
2
3
4
图12
答案 5个
解析 若某点到两波源的路程差为波长的整数倍,即Δx=nλ(n=0,1,2…),则该点振动加强,
1
2
3
4
返回
若某点到两波源的路程差为半波长的奇数倍,即Δx=
(2n+1)(n=0,1,2…),则该点振动减弱.
直线PQ上的O点距两波源A、B的路程差最大,即AO-BO=(6-1)
m=
5
m=
λ,
故O点为减弱点,由O向-∞或由O向+∞,直线PQ上各点到两波源A、B的路程差逐渐减小,
所以在直线PQ上从-∞到+∞的范围内听不到声音的区域共有5个.
KE
SHI
DUI
DIAN
LIAN
课时对点练
4
考点一 波的叠加
1.两列波在某区域相遇,下列说法正确的是
A.两列波相遇时运动状态互相干扰
B.由于这两列波相遇时叠加,当它们分开时波的频率、振幅都会发生变化
C.这两列波叠加以后一定会产生干涉图样
D.两列波重叠的区域里,任何一点的总位移都等于两列波分别引起的位
移的矢量和
基础对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 由波的独立传播特性和波的叠加原理可知,选项D正确,A、B错误;
只有频率相同、相位差恒定的两列波叠加后才能发生干涉现象,产生干涉图样,选项C错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
2.关于波的叠加和干涉,下列说法正确的是
A.两列频率不相同的波相遇时,因为没有稳定的干涉图样,所以波没有
叠加
B.两列频率相同的波相遇时,振动加强的点只是波峰与波峰相遇的点
C.两列频率相同的波相遇时,介质中振动加强的质点在某时刻的位移可
能是零
D.两列频率相同的波相遇时,振动加强的质点的位移总是比振动减弱的
质点的位移大
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 两列波相遇时一定叠加,没有条件,A错误;
振动加强是指振幅增大,而不只是波峰与波峰相遇,B错误;
振动加强点的振幅增大,质点仍然在自己的平衡位置附近振动,故某时刻的位移可以是振幅范围内的任何值,C正确,D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
3.(2020·河北冀州中学期中)一条弹性绳子呈水平状态.M为绳子中点(图中未画出),两端P、Q同时开始上下振动,一小段时间后产生的波形如图1所示.对于其后绳上各点的振动情况,以下判断正确的是
A.两列波将同时到达中点M
B.两列波波速之比为1∶2
C.中点M的振动总是加强的
D.M点的位移大小不可能为零
1
2
3
4
5
6
7
8
9
10
11
12
13
图1
√
解析 波在同种介质中传播,波速相同,由于M为绳子中点,所以两波同时到达M点,故A正确,B错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
由于波长不同,因此两波在M点相遇时,M点的振动并不总是加强或减弱,故C错误;
当两波刚传到M点时,此时刻位移为零,所以M点的位移大小在某时刻可能为零,故D错误.
考点二 波的干涉
4.(2020·济南市期末)内燃机、通风机等在排放各种高速气流的过程中都会发出噪声,如图2所示为某种消声器的示意图,可以用来削弱高速气流产生的噪声.一列声波沿水平管道自左向右传播,到达a处时分成上下两束波,这两束声波在b处相遇时可削弱噪声.关于此消声器,下列说法正确的是
A.利用了波的反射原理
B.利用了波的衍射原理
C.只能消除某一频率的噪声
D.可以消除某些频率的噪声
1
2
3
4
5
6
7
8
9
10
11
12
13
图2
√
5.两列振动方向相同、振幅分别为A1和A2的相干简谐横波相遇.下列说法正确的是
A.波峰与波谷相遇处质点的振幅为0
B.波峰与波峰相遇处质点离开平衡位置的位移始终为A1+A2
C.波峰与波谷相遇处质点的位移总是小于波峰与波峰相遇处质点的位移
D.波峰与波峰相遇处质点的振幅一定大于波峰与波谷相遇处质点的振幅
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 波峰与波谷相遇处质点的实际振幅为|A1-A2|,故选项A错误;
波峰与波峰相遇处,质点的振幅最大,合振幅为A1+A2,但此处质点仍处于振动状态,其位移随时间按正弦规律变化,故选项B错误;
振动减弱点和振动加强点的位移均随时间按正弦规律变化,故选项C错误;
波峰与波峰相遇时振动加强,波峰与波谷相遇时振动减弱,振动加强点的振幅大于振动减弱点的振幅,故选项D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
6.(2020·临沂市期末)如图3所示,两个相干波源S1、S2产生的波在同一种均匀介质中相遇.图中实线表示某时刻的波峰,虚线表示的是波谷,下列说法正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
A.a点的振动加强,b、c、d点的振动减弱
B.e、f两点的振动介于加强和减弱之间
C.经适当的时间后,加强点和减弱点的位置互换
D.经半个周期后,原来位于波峰的点将位于波谷,原来位于波谷的点将
位于波峰
图3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 a点是波谷和波谷相遇的点,c点是波峰和波峰相遇的点,都是振动加强点;而b、d两点都是波峰和波谷相遇的点,是振动减弱点,A错误.
e点位于加强点的连线上,为加强点;f点位于减弱点的连线上,为减弱点,B错误.
相干波源产生的波的干涉是稳定的,加强点与减弱点不会随时间变化,C错误.
因形成干涉图样的质点也在不停地做周期性振动,经半个周期原来位于波峰的点将位于波谷,原来位于波谷的点将位于波峰,D正确.
7.在学校运动场上50
m直跑道的两端,分别安装了由同一信号发生器带动的两个相同的扬声器.两个扬声器连续发出波长为5
m的声波.一同学从该跑道的中点出发,向某一端点缓慢行进10
m.在此过程中,他听到扬声器声音由强变弱的次数为
A.2
B.4
C.6
D.8
1
2
3
4
5
6
7
8
9
10
11
12
13
√
解析 根据波的干涉的加强点和减弱点的条件,可知当某点与两个波源距离差为波长的整数倍时,该点为振动加强点,即声音加强点,由题意可知,Δx=nλ=5n(n=0,1,2…),所以这位同学距离跑道两端相差5
m的整数倍时,即这位同学每向前运动2.5
m,就为一个声音加强点,10
m内共有5个加强点(包括两端),则由强变弱的次数为4次,故选B.
8.(2020·威海市期末)固定在同一个振动片上的两根细杆,当振动片振动时,两根细杆周期性地触动水面,形成两个波源.两列波相遇后,形成稳定的干涉图样,图4仅为示意图.已知两波源间的距离为0.6
m,波长为0.25
m,下列判断正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
A.两波源的频率相同,相位差恒定
B.振动加强区域各质点的振动频率为波源的2倍
C.在水面上放一树叶,树叶会振动着向水槽边缘飘去
D.两波源的连线上振动加强的位置有4处
图4
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 能形成稳定的干涉图样,两列波必须频率相同,相位差恒定,A正确,B错误;
树叶会上、下振动,但不会沿波的传播方向移动,故C错误;
设s1、s2为两波源连线上某点到两波源的距离,两波源连线上的加强点应满足|s1-s2|=nλ(n=0,1,2,3…),n可能的取值为0、1、2,所以两波源连线上振动加强的位置有5处,D错误.
9.如图5所示为t=0时刻简谐横波a与b的波形图,其中a沿x轴正方向传播,b沿x轴负方向传播,波速都是10
m/s,振动方向都平行于y轴.下列选项画出的是平衡位置在x=2
m处的质点从t=0开始在一个周期内的振动图像,其中正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
能力提升练
图5
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 由题可知,两列波的波速相等,波长相等,则频率相等,能发生干涉.过 周期后,两列波的波峰同时到达x=2
m处的质点,则此质点振动总是加强,振幅为两列波振幅之和,即为3
cm,t=0时刻该质点从平衡位置沿y轴正方向运动,所以B正确.
10.(2020·聊城市二模)如图6所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-1.0
m和x=5.0
m处,两列波的速率均为v=2
m/s,两波源的振幅均为A=2
cm.图示为t=0时刻两列波的图像(传播方向如图所示),此刻平衡位置处于x=1.0
m和x=3.0
m的M、N两质点刚开始振动.质点P、Q的平衡位置分别处于x=2.0
m和x=2.5
m处,关于各质点运动情况判断正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
A.质点Q的起振方向沿y轴负方向
B.t=1.25
s时刻,质点M的位移为-4
cm
C.两列波能发生干涉,发生干涉后质点P处
为振动减弱点
D.两列波能发生干涉,发生干涉后质点Q处为振动减弱点
图6
√
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 M、N刚开始振动,由同侧法可知,质点M向下振动,质点N向上振动,即两列波的起振方向相反.由于两列波的传播速度相等,Q距N近,故质点N的振动形式先传播到质点Q,故质点Q的起振方向与质点N的起振方向相同,起振时沿y轴正方向,A错误;
质点M的平衡位置距两波源的距离差值为一个波长,因两列波的起振方向相反,故质点M处为振动减弱点,两列波的振幅相同,故质点M的位移始终为零,B错误;
同理可判断质点P处为振动减弱点,质点Q处为振动加强点,C正确,D错误.
11.(2021·天津市静海一中高二月考)如图7甲所示,两个相干波源S1、S2产生的波在同一均匀介质中相遇.图中实线表示波峰,虚线表示波谷,c和f分别为ae和bd的中点,则:
1
2
3
4
5
6
7
8
9
10
11
12
13
图7
(1)在a、b、c、d、e、f六点中,振动加强的点是________,振动减弱的点是________.
a、c、e
b、d、f
解析 由题图甲可知,a点是波谷与波谷相遇点,而b、d点是波峰与波谷相遇点,e点是波峰与波峰相遇点.由于当波峰与波峰相遇或波谷与波谷相遇时振动加强,当波峰与波谷相遇时振动减弱,所以a、e是振动加强点,b、d是振动减弱点;在波的传播方向上,振动加强点的连线上也是振动加强点,振动减弱点的连线上也是振动减弱点;c在振动加强点的连线上,f在振动减弱点的连线上,因此c是振动加强点,而f是振动减弱点.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)若两振源S1和S2振幅不相同,此时位移为零的点是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 若两振源S1和S2振幅不相同,波峰与波谷相遇处点的位移不为零,平衡位置相遇处点的位移为零,此时刻位移为零的点是c、f.
c、f
(3)在图乙中画出此时刻ace连线上,以a为原点的一列完整波形,标出a、c、e点.
1
2
3
4
5
6
7
8
9
10
11
12
13
答案 如图所示
12.如图8所示,S1、S2是两个同向的相干波源,相距4
m,两列相干波的波长均为λ=2
m,则在以S1、S2连线为半径、S2为圆心的圆周上共有几处振动减弱的点?
1
2
3
4
5
6
7
8
9
10
11
12
13
图8
答案 8
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 两列相干波在空间上会发生稳定的干涉现象,其振动加强或减弱由两列波波源到该点的距离差及波长决定:
当距离差Δx=nλ(n=0,1,2…)时,振动加强;当Δx=(2n+1)
(n=0,1,2…)时,振动减弱.
设圆周上某点P振动减弱.如图所示,
由干涉条件得:
|S1P-S2P|=(2n+1)
(n=0,1,2,…)
而λ=2
m,S2P=4
m,S1P:0~8
m,分别代入后可得共有8处振动减弱的点(注意是整个圆周上).
13.(2020·上海市期中)“华附讲坛”是华师附中邀请专家做前沿专题报告的常规学术活动,通常在东阶梯课室举办.图9是课室主席台的平面图,AB是讲台,S1、S2是与讲台上话筒等高的相同的喇叭,它们相互之间的位置和尺寸如图所示.专家的声音放大后经喇叭传回话筒再次放大时可能会产生啸叫.为了避免啸叫,话筒最好摆放在讲台上适当的位置,在这些
1
2
3
4
5
6
7
8
9
10
11
12
13
尖子生选练
位置上两个喇叭传来的声音因干涉而相消.已知空气中声速为v=340
m/s,专家声音的频率为f=136
Hz,忽略讲台的宽度,则:
图9
(1)求专家声音的波长λ;
答案 2.5
m
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 专家声音的波长是λ=
=2.5
m.
(2)图中B点是振动加强点还是振动减弱点,试通过计算说明判断依据;
答案 见解析
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 B点与两个声源的路程差为ΔxB=
=5
m=2λ.
即两个声源到B点的距离差为波长的整数倍,
所以B点为振动加强点.
(3)讲台上能够避免啸叫的适当位置有多少个?
答案 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
解析 设P是AB上任意的一个消音点,
则该点与两个声源的路程差应该满足ΔxP=
=±(2k+1)
(k=
0,1,2,3…),
由于P是在AB间的点,即有|ΔxP|<2λ
因此k只能取0和1,因此AB上共有4个消音点.
返回
本课结束
