数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式(共13张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式(共13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 10:49:31 | ||
图片预览





文档简介
(共13张PPT)
第四章
数列
4.2.2
等差数列的前
n
项和公式
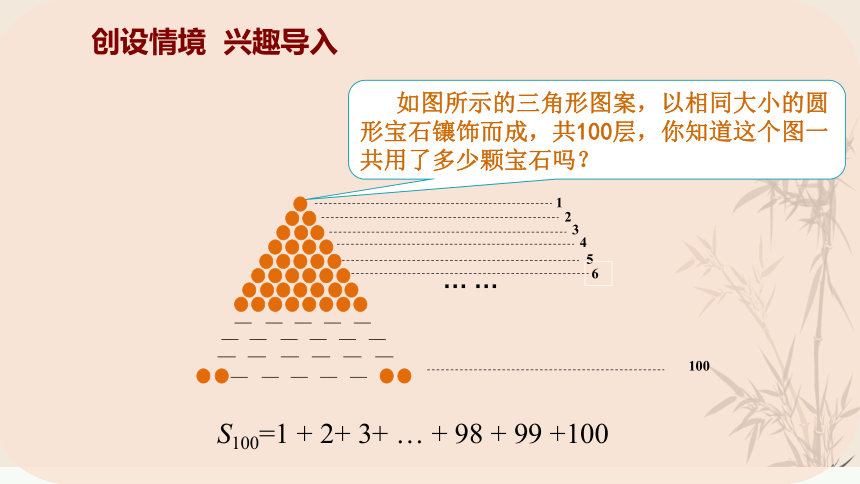
创设情境
兴趣导入
如图所示的三角形图案,以相同大小的圆形宝石镶饰而成,共100层,你知道这个图一共用了多少颗宝石吗?
S100=1
+
2+
3+
…
+
98
+
99
+100
1
2
3
4
5
6
…
…
100
1+2+3+4+…+97+98+99+100=
1+100=101
101×50=5050
2+
99=101
3+
97=101
……
50+
51=101
5050
高斯
Carl
Friedrich
Gauss
1777年-1855年,德国著名数学家
动脑思考
探索新知
解:S100=1+2+3+
…
+98+99+100
(1)
S100=100+99+98+
…
+3+
2+1
(2)
2S100=(1+100)
×100,
(1)+(2)得
问题1
求
S100=1+
2+3+
…
+98+99+100
动脑思考
探索新知
问题2
设数列
{an
}为等差数列
,求
Sn
=a1
+a2
+
a3
+…+
an-1
+an
由于
…
动脑思考
探索新知
注意1.等差数列{an
}的前
n
项和公式为
代入公式(1)得
2.将等差数列的通项公式
已知等差数列{an
}中的a1
,n,an,可用公式(1)计算
Sn
.
已知等差数列{an
}中的
a1
,n,d,可用公式(2)计算
Sn
.
动脑思考
探索新知
例5
已知等差数列{an
}中的
a1
=5,an
=95,
n=10,求S10
.
解 由已知条件可知,
a1
=5,an
=95,n=10
巩固知识
典型例题
例6
等差数列-10,-6,-2,2,…的前多少项和是54?
解
设数列的前
n
项和是54,由于
a1=-10,d
=(-6)-(-10)
=4,
即
n2-6
n-27=0,
解得
n=9或n=-3(舍去),
所以,该数列前
9
项和是
54.
故
巩固知识
典型例题
巩固知识
典型例题
1.已知等差数列
{
an
}
的首项为
a1
,公差为
d
,项数为
n
,第
n
项为
an
,前
n
项和为
Sn
,请填写下表:
a1
d
n
an
sn
5
0
20
7
4
28
12
-6
21
6
5
80
5
100
70
7
-3
7
28
4
应用知识
强化练习
应用知识
强化练习
说明:两个等差数列的求和公式及通项公式,一共涉及到
5
个量,通常已知其中
3
个,可求另外
2
个.
应用知识
强化练习
练习5.2.2
2.
在等差数列{an}中,a1
=3,a50
=101
,求S50
.
3.
在等差数列{an}中,a1
=3,
,求S10
.
归纳小结,强化思想
第四章
数列
4.2.2
等差数列的前
n
项和公式
创设情境
兴趣导入
如图所示的三角形图案,以相同大小的圆形宝石镶饰而成,共100层,你知道这个图一共用了多少颗宝石吗?
S100=1
+
2+
3+
…
+
98
+
99
+100
1
2
3
4
5
6
…
…
100
1+2+3+4+…+97+98+99+100=
1+100=101
101×50=5050
2+
99=101
3+
97=101
……
50+
51=101
5050
高斯
Carl
Friedrich
Gauss
1777年-1855年,德国著名数学家
动脑思考
探索新知
解:S100=1+2+3+
…
+98+99+100
(1)
S100=100+99+98+
…
+3+
2+1
(2)
2S100=(1+100)
×100,
(1)+(2)得
问题1
求
S100=1+
2+3+
…
+98+99+100
动脑思考
探索新知
问题2
设数列
{an
}为等差数列
,求
Sn
=a1
+a2
+
a3
+…+
an-1
+an
由于
…
动脑思考
探索新知
注意1.等差数列{an
}的前
n
项和公式为
代入公式(1)得
2.将等差数列的通项公式
已知等差数列{an
}中的a1
,n,an,可用公式(1)计算
Sn
.
已知等差数列{an
}中的
a1
,n,d,可用公式(2)计算
Sn
.
动脑思考
探索新知
例5
已知等差数列{an
}中的
a1
=5,an
=95,
n=10,求S10
.
解 由已知条件可知,
a1
=5,an
=95,n=10
巩固知识
典型例题
例6
等差数列-10,-6,-2,2,…的前多少项和是54?
解
设数列的前
n
项和是54,由于
a1=-10,d
=(-6)-(-10)
=4,
即
n2-6
n-27=0,
解得
n=9或n=-3(舍去),
所以,该数列前
9
项和是
54.
故
巩固知识
典型例题
巩固知识
典型例题
1.已知等差数列
{
an
}
的首项为
a1
,公差为
d
,项数为
n
,第
n
项为
an
,前
n
项和为
Sn
,请填写下表:
a1
d
n
an
sn
5
0
20
7
4
28
12
-6
21
6
5
80
5
100
70
7
-3
7
28
4
应用知识
强化练习
应用知识
强化练习
说明:两个等差数列的求和公式及通项公式,一共涉及到
5
个量,通常已知其中
3
个,可求另外
2
个.
应用知识
强化练习
练习5.2.2
2.
在等差数列{an}中,a1
=3,a50
=101
,求S50
.
3.
在等差数列{an}中,a1
=3,
,求S10
.
归纳小结,强化思想
