1.3.1 空间直角坐标系课件(共16张PPT)
文档属性
| 名称 | 1.3.1 空间直角坐标系课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 468.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 12:48:35 | ||
图片预览






文档简介
(共16张PPT)
第一章
统计案例
1.3.1
空间直角坐标系
高二数学选择性必修第一册
第一章
空间向量与立体几何
学习目标
1.理解空间坐标系;
2.掌握空间向量的坐标表示、正交分解的概念;
3.会用空间坐标系解决立体几何的简单问题.
4.核心素养:数学抽象、直观想象、数学运算。
一、回顾旧知
任意不共面的三个向量都可做为空间的一个基底.
1.空间向量基本定理:
2.平面向量的正交分解及坐标表示
x
y
o
x
y
z
O
Q
P
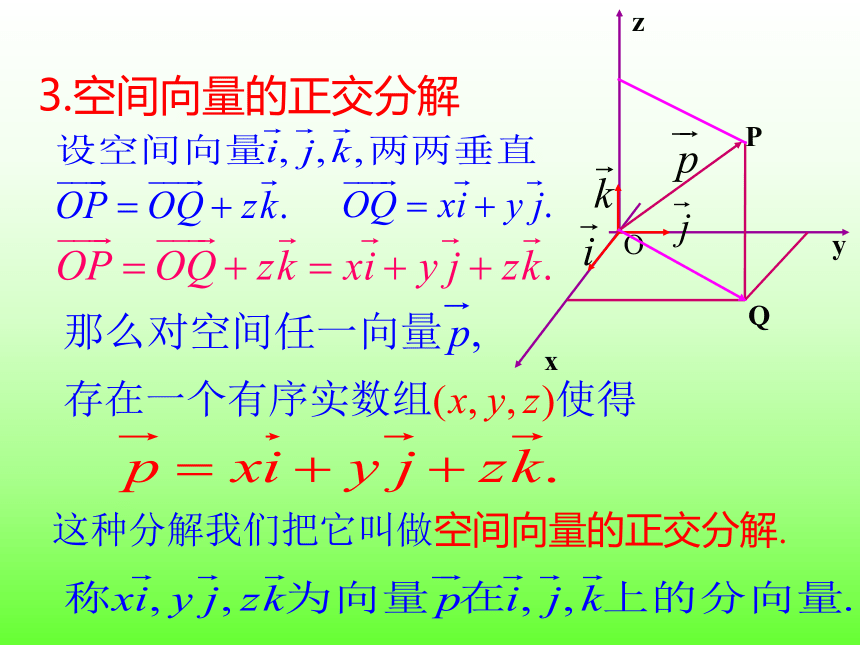
这种分解我们把它叫做空间向量的正交分解.
3.空间向量的正交分解
4.单位正交基底
(1)单位正交基底:如果空间的一个基底的三
个基向量互相垂直,且长都为1,则这个
基底叫做单位正交基底,常用表示
O
x
y
z
e1
e2
e3
O
学习新知
空间直角坐标系:在空间选定一点O和一个单位正交基底
,以点O为原点,分别以
的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系O--xyz
点O叫做原点,向量
都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,
Oyz平面,
Oxz平面。它们把空间分成八个部分
注意:画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45),∠yOz=90°.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系,本书建立的坐标系都是右手直角坐标系。
x
y
z
O
A(x,y,z)
i
j
k
向量OA的坐标恰是点A在直角坐标系Oxyz中的坐标A(x,y,z),其中x叫做点A的横坐标,y叫做点P的纵坐标,z叫做点A的竖坐标.
学习新知
在空间直角坐标系Oxyz中(如图),
为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位置由向量
唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使
在单位正交基底
下
也就是说,以O为起点的有向线段
(向量)的坐标可以和终点的坐标建立起一一对应的关系,从而互相转化.
x
y
z
O
A(x,y,z)
j
k
i
学习新知
在空间直角坐标系Oxyz中,对空间任一向量
,
作
(如图),
由空间向量基本定理,存在唯一的有序实数组(x,
y,
z),使
有序实数组(x,
y,
z),
叫做
在空间直角坐标系Oxyz中的坐标,上式可简记作
=(x,y,z).
?
A1(1,4,0)
?
A(1,4,1)
?
(2,-2,0)
B1
?
x
O
y
z
1
1
1
?
?
(-1,-3,0)
C1
?
C(-1,-3,3)
巩固1:在空间直角坐标系中作出下列各点
(1)A(1,4,1)(2)B(2,-2,-1),(3)C(-1,-3,3);
B
(2,-2,-1)
小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0.
点P的位置
原点O
X轴上A
Y轴上B
Z轴上C
坐标形式
点P的位置
坐标形式
?
O
x
y
z
1
1
1
?
A
?
D
?
C
?
B
?
E
?
F
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
6.特殊位置的点的坐标
Ⅶ
面
面
面
7.空间直角坐标系的八个卦限及坐标的符号
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅷ
点P所在卦限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
坐标符号
点P所在卦限
Ⅴ
Ⅵ
Ⅶ
Ⅷ
坐标符号
(+,+,+)
(-,+,+)
(-,-,+)
(+,-,+)
(+,+,-)
(-,+,-)
(-,-,-)
(+,-,-)
三、巩固新知
1.例1.
解:
(1)在空间坐标系o-xyz中,
(
分别是与x轴、y轴、z轴的正方向相同
的单位向量)则
的坐标为
.
(2)点M(2,-3,-4)在坐标平面xoy,xoz,yoz内
的投影的坐标分别为
,
关于原点的对称点为
,关于x轴的对称点为
.
2.变式练习
3.变式练习
解:
1.空间坐标系
四、课堂小结
2.空间向量的坐标
O
O
A(x,y,z)
作业:
课本P18
练习
3题
P22
习题1.3
3题
?
O
x
y
z
1
1
1
第一章
统计案例
1.3.1
空间直角坐标系
高二数学选择性必修第一册
第一章
空间向量与立体几何
学习目标
1.理解空间坐标系;
2.掌握空间向量的坐标表示、正交分解的概念;
3.会用空间坐标系解决立体几何的简单问题.
4.核心素养:数学抽象、直观想象、数学运算。
一、回顾旧知
任意不共面的三个向量都可做为空间的一个基底.
1.空间向量基本定理:
2.平面向量的正交分解及坐标表示
x
y
o
x
y
z
O
Q
P
这种分解我们把它叫做空间向量的正交分解.
3.空间向量的正交分解
4.单位正交基底
(1)单位正交基底:如果空间的一个基底的三
个基向量互相垂直,且长都为1,则这个
基底叫做单位正交基底,常用表示
O
x
y
z
e1
e2
e3
O
学习新知
空间直角坐标系:在空间选定一点O和一个单位正交基底
,以点O为原点,分别以
的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系O--xyz
点O叫做原点,向量
都叫做坐标向量.通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,
Oyz平面,
Oxz平面。它们把空间分成八个部分
注意:画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45),∠yOz=90°.
在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系,本书建立的坐标系都是右手直角坐标系。
x
y
z
O
A(x,y,z)
i
j
k
向量OA的坐标恰是点A在直角坐标系Oxyz中的坐标A(x,y,z),其中x叫做点A的横坐标,y叫做点P的纵坐标,z叫做点A的竖坐标.
学习新知
在空间直角坐标系Oxyz中(如图),
为坐标向量,对空间任意一点A,对应一个向量OA,且点A的位置由向量
唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使
在单位正交基底
下
也就是说,以O为起点的有向线段
(向量)的坐标可以和终点的坐标建立起一一对应的关系,从而互相转化.
x
y
z
O
A(x,y,z)
j
k
i
学习新知
在空间直角坐标系Oxyz中,对空间任一向量
,
作
(如图),
由空间向量基本定理,存在唯一的有序实数组(x,
y,
z),使
有序实数组(x,
y,
z),
叫做
在空间直角坐标系Oxyz中的坐标,上式可简记作
=(x,y,z).
?
A1(1,4,0)
?
A(1,4,1)
?
(2,-2,0)
B1
?
x
O
y
z
1
1
1
?
?
(-1,-3,0)
C1
?
C(-1,-3,3)
巩固1:在空间直角坐标系中作出下列各点
(1)A(1,4,1)(2)B(2,-2,-1),(3)C(-1,-3,3);
B
(2,-2,-1)
小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0.
点P的位置
原点O
X轴上A
Y轴上B
Z轴上C
坐标形式
点P的位置
坐标形式
?
O
x
y
z
1
1
1
?
A
?
D
?
C
?
B
?
E
?
F
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
6.特殊位置的点的坐标
Ⅶ
面
面
面
7.空间直角坐标系的八个卦限及坐标的符号
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
Ⅵ
Ⅷ
点P所在卦限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
坐标符号
点P所在卦限
Ⅴ
Ⅵ
Ⅶ
Ⅷ
坐标符号
(+,+,+)
(-,+,+)
(-,-,+)
(+,-,+)
(+,+,-)
(-,+,-)
(-,-,-)
(+,-,-)
三、巩固新知
1.例1.
解:
(1)在空间坐标系o-xyz中,
(
分别是与x轴、y轴、z轴的正方向相同
的单位向量)则
的坐标为
.
(2)点M(2,-3,-4)在坐标平面xoy,xoz,yoz内
的投影的坐标分别为
,
关于原点的对称点为
,关于x轴的对称点为
.
2.变式练习
3.变式练习
解:
1.空间坐标系
四、课堂小结
2.空间向量的坐标
O
O
A(x,y,z)
作业:
课本P18
练习
3题
P22
习题1.3
3题
?
O
x
y
z
1
1
1
