1.4.1正弦函数、余弦函数的图像课件-2021-2022学年高一下学期数学人教A版必修四(共15张PPT)
文档属性
| 名称 | 1.4.1正弦函数、余弦函数的图像课件-2021-2022学年高一下学期数学人教A版必修四(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
1)了解用正弦线画正弦函数的图象的原理;
2)熟练掌握用“五点法”作正、余弦函数的图象
;
3)理解正弦函数与余弦函数图象的变换关系。
学习目标:
1、知识与技能:
2、过程与方法:
3、情感态度与价值观:
通过主动参与,体验知识的形成过程,加深对正余弦函
数图象的认知。
培养联系和运动的观点,善于运用类比和联想,对数形结合有进一步的认识,形成良好的数学品质。
教学重点和难点:
重点:
用“五点法”作函数的图象。
难点:利用正弦线作正弦函数的图象
。
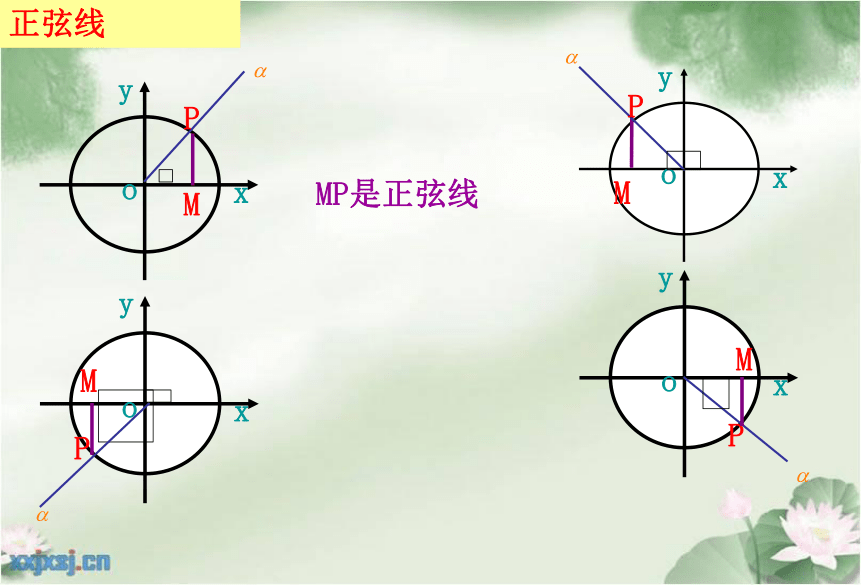
正弦线
y
x
o
M
P
MP是正弦线
y
x
o
M
P
y
x
o
M
P
y
x
o
P
M
1
-1
0
y
x
●
●
●
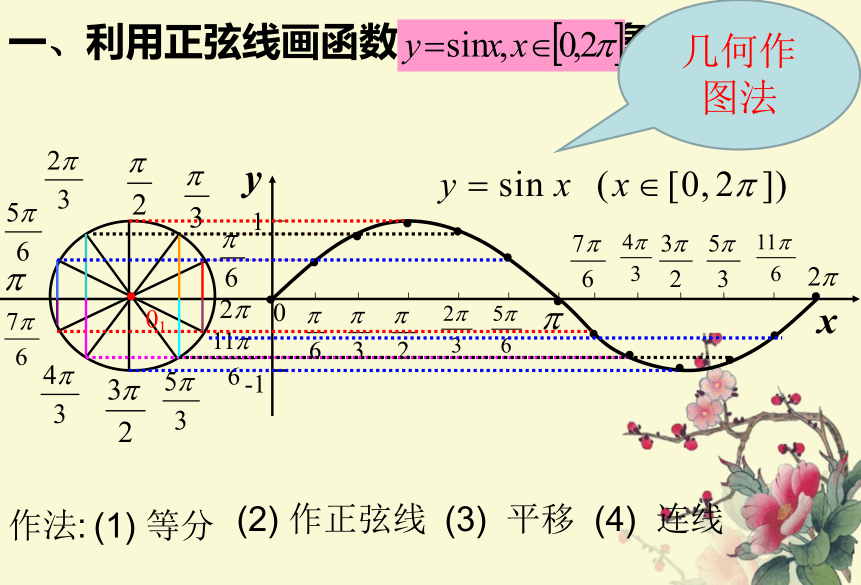
一、利用正弦线画函数
的图象
●
●
●
●
●
●
●
●
●
●
●
01
作法:
(1)
等分
(2)
作正弦线
(3)
平移
(4)
连线
几何作图法
y
x
o
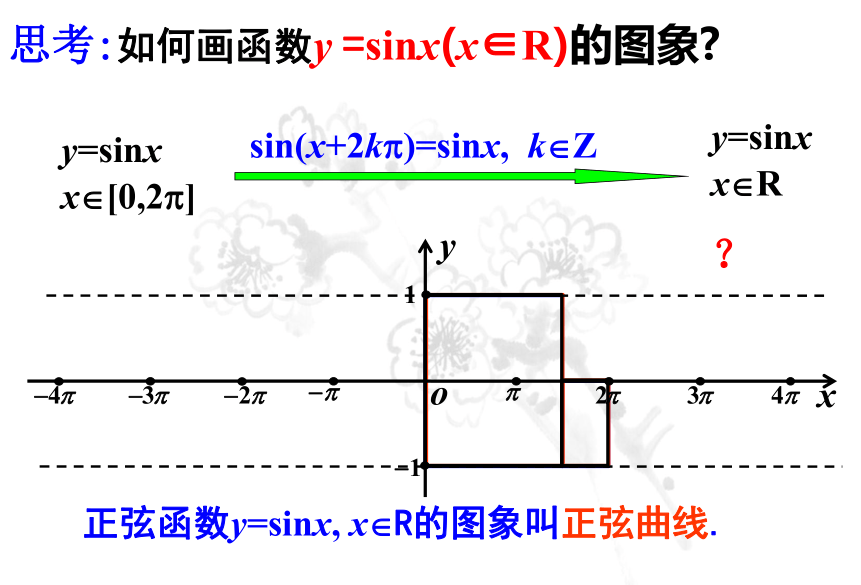
思考:如何画函数y
=sinx(x∈R)的图象?
y=sinx
x?[0,2?]
y=sinx
x?R
?
sin(x+2k?)=sinx,
k?Z
正弦函数y=sinx,
x?R的图象叫正弦曲线.
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
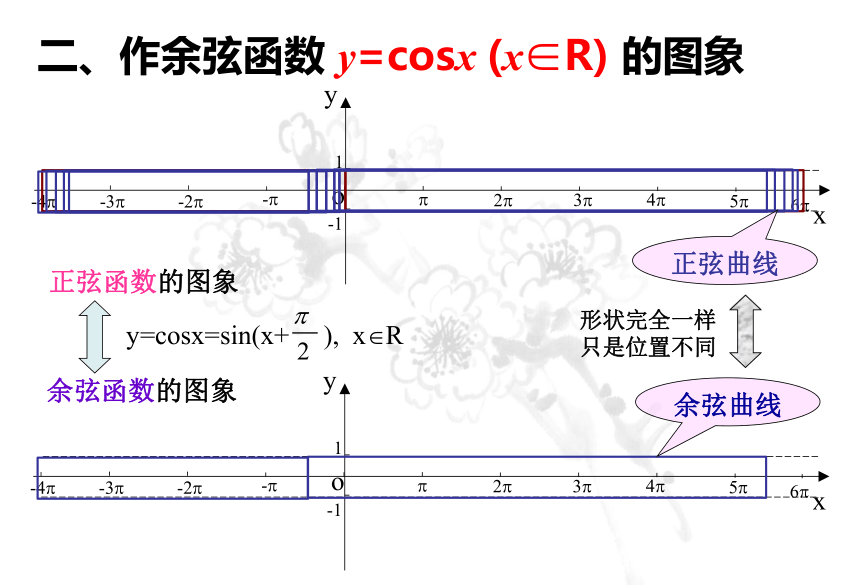
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+
),
x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
二、作余弦函数
y=cosx
(x∈R)
的图象
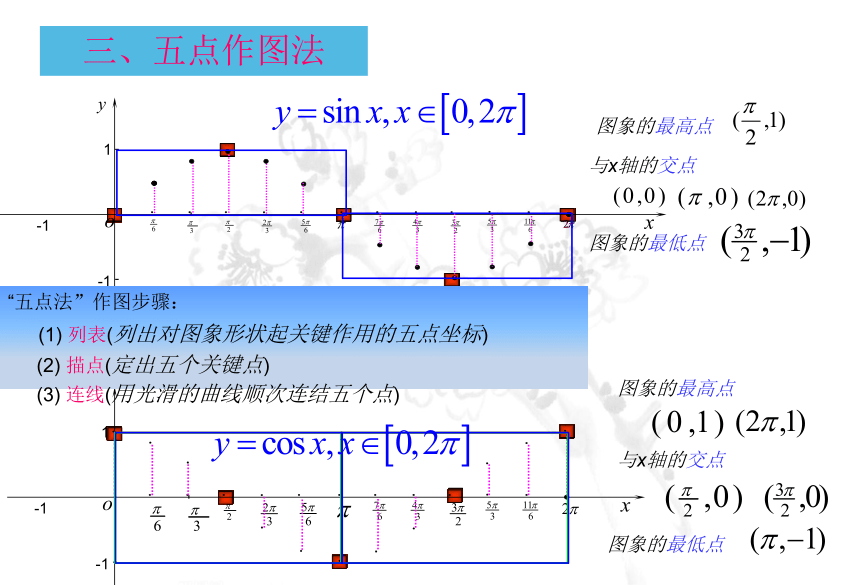
三、五点作图法
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
-
-
-1
1
-
-1
-
-
-1
1
-
-1
“五点法”作图步骤:
(1)
列表(列出对图象形状起关键作用的五点坐标)
(3)
连线(用光滑的曲线顺次连结五个点)
(2)
描点(定出五个关键点)
例1
(1)画出函数y=1+sinx,x?[0,
2?]的简图:
x
sinx
1+sinx
0
0
1
0
-1
0
o
1
y
x
-1
2
y=sinx,x?[0,
2?]
y=1+sinx,x?[0,
2?]
步骤:
1.列表
2.描点
3.连线
例题讲解
1
2
1
0
1
(2)
画出函数y=
-
cosx,x?[0,
2?]的简图:
x
cosx
-
cosx
1
0
-1
0
1
y
x
o
1
-1
y=
-
cosx,x?[0,
2?]
y=cosx,x?[0,
2?]
-1
0
1
0
-1
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
D
的大致图象为(
)
x∈[0,2π]
函数y=1-cosx,
x
y
O
2π
π
1
-1
例2:当x∈[0,2π]时,求不等式
的解集.
x
-1
O
2π
π
1
y
变式
当x∈[0,2π]时,求不等式
的解集.
小结:
知识:
1、正弦函数图象的几何作图方法。
2、正、余弦函数图象的五点法作图方法。
3、与正、余弦函数图像有关的图象变换。
能力:会画简图,会应用图象。
思想:数形结合,运动变化。
作业设计:
1.必做题:课本P46A组第1题;
2.选做题:
1)了解用正弦线画正弦函数的图象的原理;
2)熟练掌握用“五点法”作正、余弦函数的图象
;
3)理解正弦函数与余弦函数图象的变换关系。
学习目标:
1、知识与技能:
2、过程与方法:
3、情感态度与价值观:
通过主动参与,体验知识的形成过程,加深对正余弦函
数图象的认知。
培养联系和运动的观点,善于运用类比和联想,对数形结合有进一步的认识,形成良好的数学品质。
教学重点和难点:
重点:
用“五点法”作函数的图象。
难点:利用正弦线作正弦函数的图象
。
正弦线
y
x
o
M
P
MP是正弦线
y
x
o
M
P
y
x
o
M
P
y
x
o
P
M
1
-1
0
y
x
●
●
●
一、利用正弦线画函数
的图象
●
●
●
●
●
●
●
●
●
●
●
01
作法:
(1)
等分
(2)
作正弦线
(3)
平移
(4)
连线
几何作图法
y
x
o
思考:如何画函数y
=sinx(x∈R)的图象?
y=sinx
x?[0,2?]
y=sinx
x?R
?
sin(x+2k?)=sinx,
k?Z
正弦函数y=sinx,
x?R的图象叫正弦曲线.
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+
),
x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
二、作余弦函数
y=cosx
(x∈R)
的图象
三、五点作图法
与x轴的交点
图象的最高点
图象的最低点
与x轴的交点
图象的最高点
图象的最低点
-
-
-1
1
-
-1
-
-
-1
1
-
-1
“五点法”作图步骤:
(1)
列表(列出对图象形状起关键作用的五点坐标)
(3)
连线(用光滑的曲线顺次连结五个点)
(2)
描点(定出五个关键点)
例1
(1)画出函数y=1+sinx,x?[0,
2?]的简图:
x
sinx
1+sinx
0
0
1
0
-1
0
o
1
y
x
-1
2
y=sinx,x?[0,
2?]
y=1+sinx,x?[0,
2?]
步骤:
1.列表
2.描点
3.连线
例题讲解
1
2
1
0
1
(2)
画出函数y=
-
cosx,x?[0,
2?]的简图:
x
cosx
-
cosx
1
0
-1
0
1
y
x
o
1
-1
y=
-
cosx,x?[0,
2?]
y=cosx,x?[0,
2?]
-1
0
1
0
-1
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
o
1
y
x
-1
2
D
的大致图象为(
)
x∈[0,2π]
函数y=1-cosx,
x
y
O
2π
π
1
-1
例2:当x∈[0,2π]时,求不等式
的解集.
x
-1
O
2π
π
1
y
变式
当x∈[0,2π]时,求不等式
的解集.
小结:
知识:
1、正弦函数图象的几何作图方法。
2、正、余弦函数图象的五点法作图方法。
3、与正、余弦函数图像有关的图象变换。
能力:会画简图,会应用图象。
思想:数形结合,运动变化。
作业设计:
1.必做题:课本P46A组第1题;
2.选做题:
