2021-2022学年沪科版 八年级数学上册11.2图形在坐标系中的平移 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版 八年级数学上册11.2图形在坐标系中的平移 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 852.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 18:27:52 | ||
图片预览




文档简介
11.2图形在坐标系中的平移
基础强化
选择题
1.在直角坐标系中将图形所有点的横坐标都减去3,纵坐标不变,则所得图形与原图形相比是()
A.向右平移的3个单位B.向上平移的3个单位
C.向左平移的3个单位D.向下平移的3个单位
2.在平面直角坐标系中,将点A(2,5)向左平移3个单位后得到的点位于()
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.线段CD是由线段AB平移得到的,点A(-2,3)对应的点为C(3,6),则B(-6,5)对应点D的坐标为()
A(1,9)
B(-1,-8)
C(1,-8)
D(-1,8)
4.△DEF是由△ABC平移得到的,点A(-2,-5)的对应点D(2,-1),则点B(2,2)对应点E的坐标为()
A(6,2)
B(6,-2)
C(-6,2)
D(-6,-2)
5.已知三角形的三个顶点坐标分别为(-4,-1),(1,1),(-1,4),现将三角形先向右平移2个单位,再向上平移3个单位,则平移后的三角形的三个顶点的坐标是()
A(-2,2)(3,4)(1,7)
B(-2,2)(4,3)(1,7)
C(2,2)(3,4)(1,7)
D(2,-2)(3,3)(1,7)
6.线段AB两端点坐标分别为A(),B(),现将它向左平移4个单位长度,得到线段A1B1,则A1、B1的坐标分别为(
)
A.A1(),B1()
B.A1(),
B1(0,5)
C.A1()
B1(-8,1)
D.A1()
B1()
7.已知平面直角坐标系中点.将它沿轴方向向上平移3个单位所得点的坐标是
A.
B.
C.
D.
8.如图,点,的坐标分别为,,若将线段平移至的位置,点,的坐标分别为,,则的值为
A.2
B.3
C.4
D.5
9.如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是
A.(1,
7)
,
(-2,
2),(3,
4).
B.
(1,
7)
,
(-2,
2),(4,
3).
C.(1,
7)
,
(2,
2),(3,
4).
D.
(1,
7)
,
(2,-2),(3,
3).
10.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为(
).
A.(-2,-5)
B.(-2,5)
C.(2,-5)
D.(2,5)
填空题
11.小华将直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为(-4,3),(-2,3),则移动后猫眼的坐标为_________.
12.在平面直角坐标系中,将点向左平移2个单位长度得到的点的坐标是 .
13.点A(1,1)是由(-2,1)向__移动__个单位长度得到的.
14.点A(1,1)是由(5,-2)向__移动__个单位长度,再向__移动__个单位长度得到的.
15.线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________.
16.已知点,将点向左平移3个单位长度后落在轴上,则的坐标是 .
简答题
指出下列平移变换的方向和距离:
P(2,5)
P’(2,-7)
P(-1,-3)
P’(4,-3)
18.△ABC三个顶点的坐标
A(4,3),B(3,1),C(1,2)
(1)建立直角坐标系,并在直角坐标系中画出△ABC
(2)将三角形△ABC
经过平移得到△DEF,已知点C(1,2)的对应点F(-5,2)求点D点E的坐标,并画出△DEF.
19.如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形的顶点的坐标为,顶点的坐标为,顶点的坐标为.
(1)把三角形向右平移5个单位长度,再向下平移4个单位长度得到三角形,请你画出三角形;
(2)请直接写出点,,的坐标;
(3)求三角形的面积.
20.在平面直角坐标系中,线段的两端点的坐标分别为,,将线段向下平移2个单位,再向右平移4个单位得线段与对应,与对应).
(1)画出线段与线段,并求点、点的坐标.
(2)求四边形的面积
21.在平面直角坐标系中,点的坐标为,线段的位置如图所示,其中点的坐标为,点的坐标为.
(1)将线段平移得到线段,其中点的对应点为,点的对称点为.
①点平移到点的过程可以是:先向
平移 个单位长度,再向 平移 个单位长度;
②点的坐标为 ;
(2)在(1)的条件下,若点的坐标为,连接,,求的面积.
(3)在轴上是否存在点,使以、、三点为顶点的三角形的面积为3,若存在,请直接写出点的坐标;若不存在,请说明理由.
参考答案
选择题
1.C
2.B
3.D
4.B
5.A
6.C
7.B
8.A
9.A
10.A
填空题
(-1,3),(1,3)
左
3
右
4
左
3
(1,2)
解答题
17.
向下平移12个单位
向右平移5个单位
18.图略
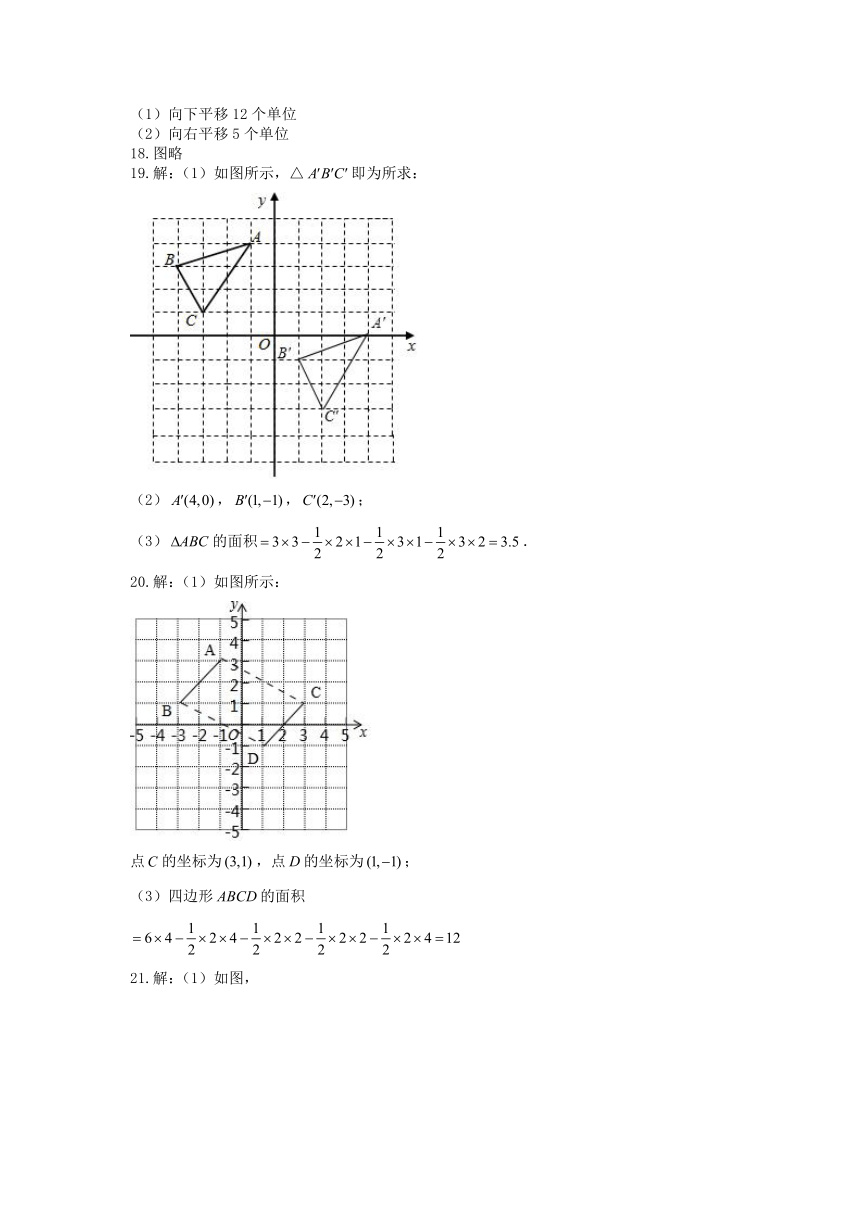
19.解:(1)如图所示,△即为所求:
(2),,;
(3)的面积.
20.解:(1)如图所示:
点的坐标为,点的坐标为;
四边形的面积
21.解:(1)如图,
①点平移到点的过程可以是:先向右平移3单位长度,再向上平移5个单位长度;
故答案为:右、3、上、5.
②,
故答案为.
(2)如图,
(3)存在.设,由题意,
解得或5,
点坐标为或.
拓展培优
选择题
1.如图,在平面直角坐标系中,已知点,点.平移线段,使点落在点处,则点的对应点的坐标为
A.
B.
C.
D.
2.下列图形中,周长不是32m的图形是(
)
A.
B.
C.
D.
3.如图,把图①中的经过一定的变换得到图②中的,如果图①中上点的坐标为,那么这个点在图②中的对应点的坐标为(
)
A.
B.
C.
D.
4.的顶点A的坐标为(-2,5),若将沿轴平移5个单位长度,则A点的坐标变为(
)
A.(3,5)
B.(3,0)或(-7,0)
C.(3,5)或(-7,5)
D.(-2,0)或(-2,10)
5.如图,的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),现将B点向右平移2个单位后,在向上平移4个单位得到点B1。设的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系是(
)
A.S1=S2
B.S1>S2
C.S1≥S2
D.S1填空题
6.已知在轴上,在轴上,则向左平移2个单位长度再向上平移3个单位长度后的坐标为 .
7.如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(),(4,0)。把△OAB沿轴平移到△CDE。若点D的坐标为(),则点E的坐标为
。
8.如图,将边长为1的正三角形沿轴正方向连续翻转2022次,点依次落在的位置,则点的横坐标为
.
已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿轴向左平移使点C与坐标原点重合后,再沿轴向下平移到使点D与坐标原点重合,此时点B的坐标是
。
10.已知点M的坐标为(2,-4),将平面直角坐标系向右平移
个单位,再向
平移
个单位,可使点M与原点重合。
解答题
11.如图,点,的坐标分别为,,若将线段平移到的坐标分别为,,试求的值.
12.在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
(1)分别求出线段AB中点,线段AC中点及线段CD中点的坐标,则线段AB
中点的坐标与点A,B的坐标之间有什么关系?对线段AC中点和点A,C及线段CD中点和点C,D成立吗?
(2)已知点M(a,0),N(b,0),请写出线段MN的中点P的坐标.
13.在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1㎝,整点P从原点O出发,速度为1㎝/s,且整点P只做向右或向上运动,则运动1s后它可以到达(0,1)、(1,0)两个整点;它运动2s后可以到达(2,0)、(1,1)、(0,2)三个整点;运动3s后它可以到达(3,0)、(2,1)、(1,2)、(0,
3)四个整点;……
请探索并回答下面问题:
①当整点P从点O出发4s后可以到达的整点共有
个;
②在直角坐标系中描出:整点P从点O出发8s后所能到达的整点,并观察这些整点,说出它们在位置上有什么特点?
③当整点P从点O出发
s后可到达整点(13,5)的位置.
14.如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3。已知A(1,3)A1
(2,3)A2(4,3)
A3(8,3);B(2,0),B1(4,0)
B2
(8,0)
B3(16,0)。
⑴
观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是
,B4的坐标是
。
⑵
若按第一题找出的规律,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是
,Bn的坐标是
。
参考答案
一、选择题
1.B
2.B
3.C
4.C
5.A
二、填空题
6.解:在轴上,
,
解得:,
在轴上,
,
解得:,
点坐标为,
向左平移2个单位长度再向上平移3个单位长度,
所的对应点坐标为,
即,
故答案为:.
7.(7,0)
8.2021.5
9.(-5,-3)
10.2
下
4
三、解答题
11.解:,,,,
平移方法为向右平移1个单位,向上平移1个单位,
,,
.
(1)线段AB中点坐标为(3,0),
线段AC中点坐标为(0.5,0),
线段CD中点的坐标为(-2,0),
线段AB中点的坐标是点A,B的坐标的和的一半,
对线段AC中点和点A,C及线段CD中点和点C,D成立;
(2)线段MN的中点P的坐标为(,0)
13.
解:(1)出发4s后可以到达的点有(4,0),(1,3),(2,2),(3,1),(0,4)共5个;
(2)如图,共有9个点,它们在同一直线上;
(3)∵13+5=18,
∴整点P从点O出发18s后可到达整点(13,5)的位置.
故答案是:18.
14.
(1)因为A(1,3),A1(2,3),A2(4,3),A3(8,3)…纵坐标不变为3,横坐标都和2有关,为2n,那么A4(16,3);
因为B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,横坐标都和2有关为2n+1,那么B的坐标为B4(32,0);
(2)由上题规律可知An的纵坐标总为3,横坐标为2n,Bn的纵坐标总为0,横坐标为2n+1
基础强化
选择题
1.在直角坐标系中将图形所有点的横坐标都减去3,纵坐标不变,则所得图形与原图形相比是()
A.向右平移的3个单位B.向上平移的3个单位
C.向左平移的3个单位D.向下平移的3个单位
2.在平面直角坐标系中,将点A(2,5)向左平移3个单位后得到的点位于()
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.线段CD是由线段AB平移得到的,点A(-2,3)对应的点为C(3,6),则B(-6,5)对应点D的坐标为()
A(1,9)
B(-1,-8)
C(1,-8)
D(-1,8)
4.△DEF是由△ABC平移得到的,点A(-2,-5)的对应点D(2,-1),则点B(2,2)对应点E的坐标为()
A(6,2)
B(6,-2)
C(-6,2)
D(-6,-2)
5.已知三角形的三个顶点坐标分别为(-4,-1),(1,1),(-1,4),现将三角形先向右平移2个单位,再向上平移3个单位,则平移后的三角形的三个顶点的坐标是()
A(-2,2)(3,4)(1,7)
B(-2,2)(4,3)(1,7)
C(2,2)(3,4)(1,7)
D(2,-2)(3,3)(1,7)
6.线段AB两端点坐标分别为A(),B(),现将它向左平移4个单位长度,得到线段A1B1,则A1、B1的坐标分别为(
)
A.A1(),B1()
B.A1(),
B1(0,5)
C.A1()
B1(-8,1)
D.A1()
B1()
7.已知平面直角坐标系中点.将它沿轴方向向上平移3个单位所得点的坐标是
A.
B.
C.
D.
8.如图,点,的坐标分别为,,若将线段平移至的位置,点,的坐标分别为,,则的值为
A.2
B.3
C.4
D.5
9.如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是
A.(1,
7)
,
(-2,
2),(3,
4).
B.
(1,
7)
,
(-2,
2),(4,
3).
C.(1,
7)
,
(2,
2),(3,
4).
D.
(1,
7)
,
(2,-2),(3,
3).
10.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为(
).
A.(-2,-5)
B.(-2,5)
C.(2,-5)
D.(2,5)
填空题
11.小华将直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为(-4,3),(-2,3),则移动后猫眼的坐标为_________.
12.在平面直角坐标系中,将点向左平移2个单位长度得到的点的坐标是 .
13.点A(1,1)是由(-2,1)向__移动__个单位长度得到的.
14.点A(1,1)是由(5,-2)向__移动__个单位长度,再向__移动__个单位长度得到的.
15.线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________.
16.已知点,将点向左平移3个单位长度后落在轴上,则的坐标是 .
简答题
指出下列平移变换的方向和距离:
P(2,5)
P’(2,-7)
P(-1,-3)
P’(4,-3)
18.△ABC三个顶点的坐标
A(4,3),B(3,1),C(1,2)
(1)建立直角坐标系,并在直角坐标系中画出△ABC
(2)将三角形△ABC
经过平移得到△DEF,已知点C(1,2)的对应点F(-5,2)求点D点E的坐标,并画出△DEF.
19.如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形的顶点的坐标为,顶点的坐标为,顶点的坐标为.
(1)把三角形向右平移5个单位长度,再向下平移4个单位长度得到三角形,请你画出三角形;
(2)请直接写出点,,的坐标;
(3)求三角形的面积.
20.在平面直角坐标系中,线段的两端点的坐标分别为,,将线段向下平移2个单位,再向右平移4个单位得线段与对应,与对应).
(1)画出线段与线段,并求点、点的坐标.
(2)求四边形的面积
21.在平面直角坐标系中,点的坐标为,线段的位置如图所示,其中点的坐标为,点的坐标为.
(1)将线段平移得到线段,其中点的对应点为,点的对称点为.
①点平移到点的过程可以是:先向
平移 个单位长度,再向 平移 个单位长度;
②点的坐标为 ;
(2)在(1)的条件下,若点的坐标为,连接,,求的面积.
(3)在轴上是否存在点,使以、、三点为顶点的三角形的面积为3,若存在,请直接写出点的坐标;若不存在,请说明理由.
参考答案
选择题
1.C
2.B
3.D
4.B
5.A
6.C
7.B
8.A
9.A
10.A
填空题
(-1,3),(1,3)
左
3
右
4
左
3
(1,2)
解答题
17.
向下平移12个单位
向右平移5个单位
18.图略
19.解:(1)如图所示,△即为所求:
(2),,;
(3)的面积.
20.解:(1)如图所示:
点的坐标为,点的坐标为;
四边形的面积
21.解:(1)如图,
①点平移到点的过程可以是:先向右平移3单位长度,再向上平移5个单位长度;
故答案为:右、3、上、5.
②,
故答案为.
(2)如图,
(3)存在.设,由题意,
解得或5,
点坐标为或.
拓展培优
选择题
1.如图,在平面直角坐标系中,已知点,点.平移线段,使点落在点处,则点的对应点的坐标为
A.
B.
C.
D.
2.下列图形中,周长不是32m的图形是(
)
A.
B.
C.
D.
3.如图,把图①中的经过一定的变换得到图②中的,如果图①中上点的坐标为,那么这个点在图②中的对应点的坐标为(
)
A.
B.
C.
D.
4.的顶点A的坐标为(-2,5),若将沿轴平移5个单位长度,则A点的坐标变为(
)
A.(3,5)
B.(3,0)或(-7,0)
C.(3,5)或(-7,5)
D.(-2,0)或(-2,10)
5.如图,的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),现将B点向右平移2个单位后,在向上平移4个单位得到点B1。设的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系是(
)
A.S1=S2
B.S1>S2
C.S1≥S2
D.S1
6.已知在轴上,在轴上,则向左平移2个单位长度再向上平移3个单位长度后的坐标为 .
7.如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(),(4,0)。把△OAB沿轴平移到△CDE。若点D的坐标为(),则点E的坐标为
。
8.如图,将边长为1的正三角形沿轴正方向连续翻转2022次,点依次落在的位置,则点的横坐标为
.
已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿轴向左平移使点C与坐标原点重合后,再沿轴向下平移到使点D与坐标原点重合,此时点B的坐标是
。
10.已知点M的坐标为(2,-4),将平面直角坐标系向右平移
个单位,再向
平移
个单位,可使点M与原点重合。
解答题
11.如图,点,的坐标分别为,,若将线段平移到的坐标分别为,,试求的值.
12.在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
(1)分别求出线段AB中点,线段AC中点及线段CD中点的坐标,则线段AB
中点的坐标与点A,B的坐标之间有什么关系?对线段AC中点和点A,C及线段CD中点和点C,D成立吗?
(2)已知点M(a,0),N(b,0),请写出线段MN的中点P的坐标.
13.在平面直角坐标系中,横坐标、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1㎝,整点P从原点O出发,速度为1㎝/s,且整点P只做向右或向上运动,则运动1s后它可以到达(0,1)、(1,0)两个整点;它运动2s后可以到达(2,0)、(1,1)、(0,2)三个整点;运动3s后它可以到达(3,0)、(2,1)、(1,2)、(0,
3)四个整点;……
请探索并回答下面问题:
①当整点P从点O出发4s后可以到达的整点共有
个;
②在直角坐标系中描出:整点P从点O出发8s后所能到达的整点,并观察这些整点,说出它们在位置上有什么特点?
③当整点P从点O出发
s后可到达整点(13,5)的位置.
14.如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3。已知A(1,3)A1
(2,3)A2(4,3)
A3(8,3);B(2,0),B1(4,0)
B2
(8,0)
B3(16,0)。
⑴
观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是
,B4的坐标是
。
⑵
若按第一题找出的规律,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是
,Bn的坐标是
。
参考答案
一、选择题
1.B
2.B
3.C
4.C
5.A
二、填空题
6.解:在轴上,
,
解得:,
在轴上,
,
解得:,
点坐标为,
向左平移2个单位长度再向上平移3个单位长度,
所的对应点坐标为,
即,
故答案为:.
7.(7,0)
8.2021.5
9.(-5,-3)
10.2
下
4
三、解答题
11.解:,,,,
平移方法为向右平移1个单位,向上平移1个单位,
,,
.
(1)线段AB中点坐标为(3,0),
线段AC中点坐标为(0.5,0),
线段CD中点的坐标为(-2,0),
线段AB中点的坐标是点A,B的坐标的和的一半,
对线段AC中点和点A,C及线段CD中点和点C,D成立;
(2)线段MN的中点P的坐标为(,0)
13.
解:(1)出发4s后可以到达的点有(4,0),(1,3),(2,2),(3,1),(0,4)共5个;
(2)如图,共有9个点,它们在同一直线上;
(3)∵13+5=18,
∴整点P从点O出发18s后可到达整点(13,5)的位置.
故答案是:18.
14.
(1)因为A(1,3),A1(2,3),A2(4,3),A3(8,3)…纵坐标不变为3,横坐标都和2有关,为2n,那么A4(16,3);
因为B(2,0),B1(4,0),B2(8,0),B3(16,0)…纵坐标不变,为0,横坐标都和2有关为2n+1,那么B的坐标为B4(32,0);
(2)由上题规律可知An的纵坐标总为3,横坐标为2n,Bn的纵坐标总为0,横坐标为2n+1
