2020-2021学年山东省菏泽市牡丹区七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省菏泽市牡丹区七年级(下)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 446.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 09:47:01 | ||
图片预览


文档简介
2020-2021学年山东省菏泽市牡丹区七年级(下)期末数学试卷
一、选择题(木大题共10个小题,在每小题给出的四个选项中,只有一个选项是正确的,把正确选项的序号涂在答题卡的相应位置)
1.(3分)如图,四个图标分别是剑桥大学、北京理工大学、浙江大学和北京大学的校徽的重要组成部分,其中是轴对称图形的是( )
A.
B.
C.
D.
2.(3分)下列运算正确的是( )
A.(a+b)2=a2+b2
B.a3+3a3=4a3
C.(﹣2a2)3=6a6
D.(b+a)(a﹣b)=b2﹣a2
3.(3分)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
4.(3分)下列说法中正确的个数有( )
①平面内,过一点有且只有一条直线与已知直线垂直;
②过一点有且只有一条直线与已知直线平行;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
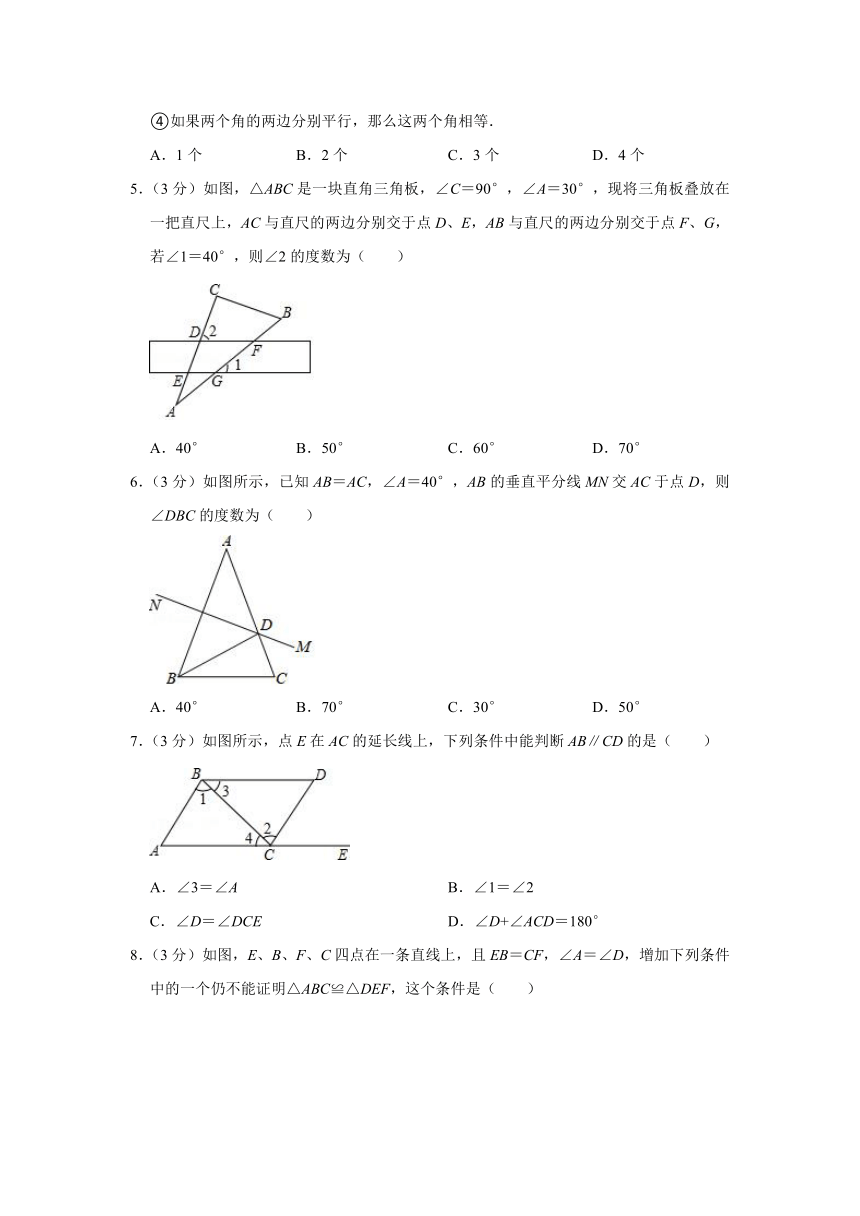
④如果两个角的两边分别平行,那么这两个角相等.
A.1个
B.2个
C.3个
D.4个
5.(3分)如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40°
B.50°
C.60°
D.70°
6.(3分)如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )
A.40°
B.70°
C.30°
D.50°
7.(3分)如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
8.(3分)如图,E、B、F、C四点在一条直线上,且EB=CF,∠A=∠D,增加下列条件中的一个仍不能证明△ABC≌△DEF,这个条件是( )
A.DF∥AC
B.AB=DE
C.∠E=∠ABC
D.AB∥DE
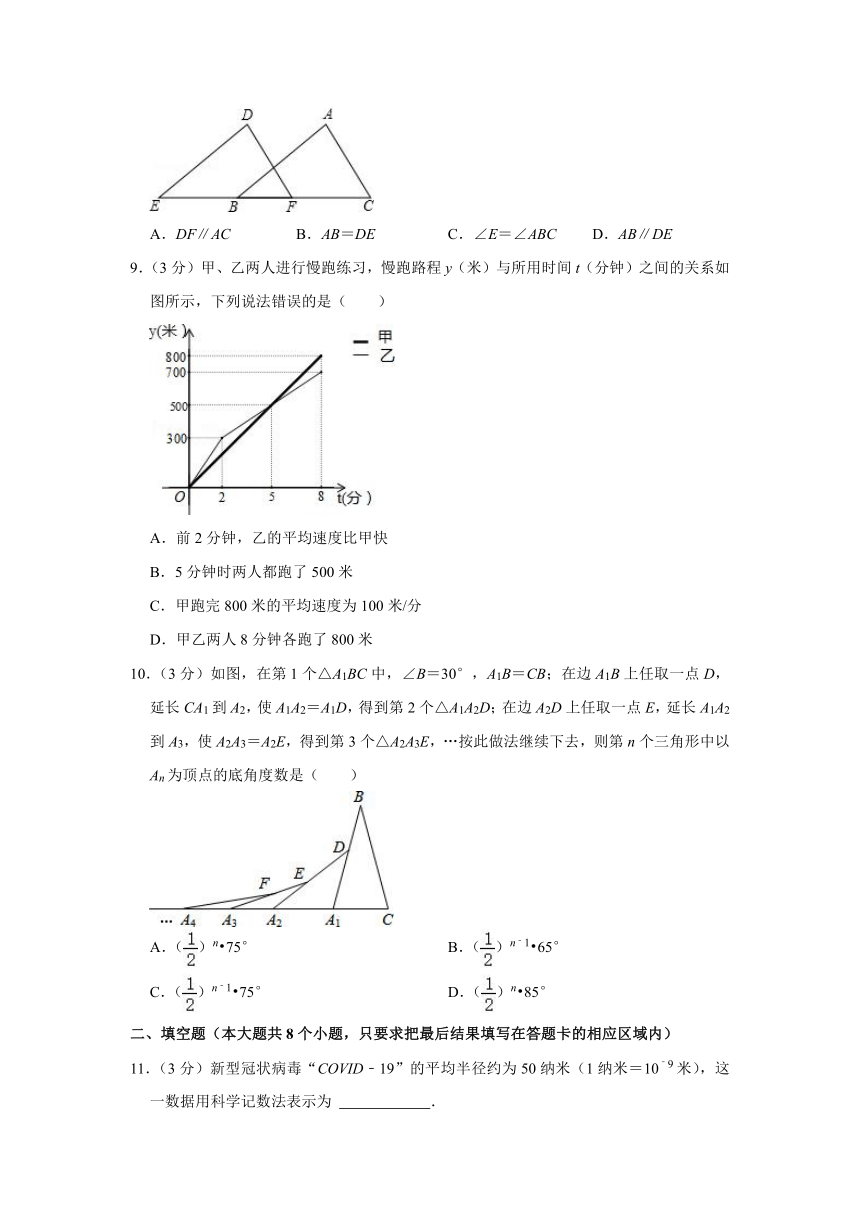
9.(3分)甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟时两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
10.(3分)如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.()n?75°
B.()n﹣1?65°
C.()n﹣1?75°
D.()n?85°
二、填空题(本大题共8个小题,只要求把最后结果填写在答题卡的相应区域内)
11.(3分)新型冠状病毒“COVID﹣19”的平均半径约为50纳米(1纳米=10﹣9米),这一数据用科学记数法表示为
.
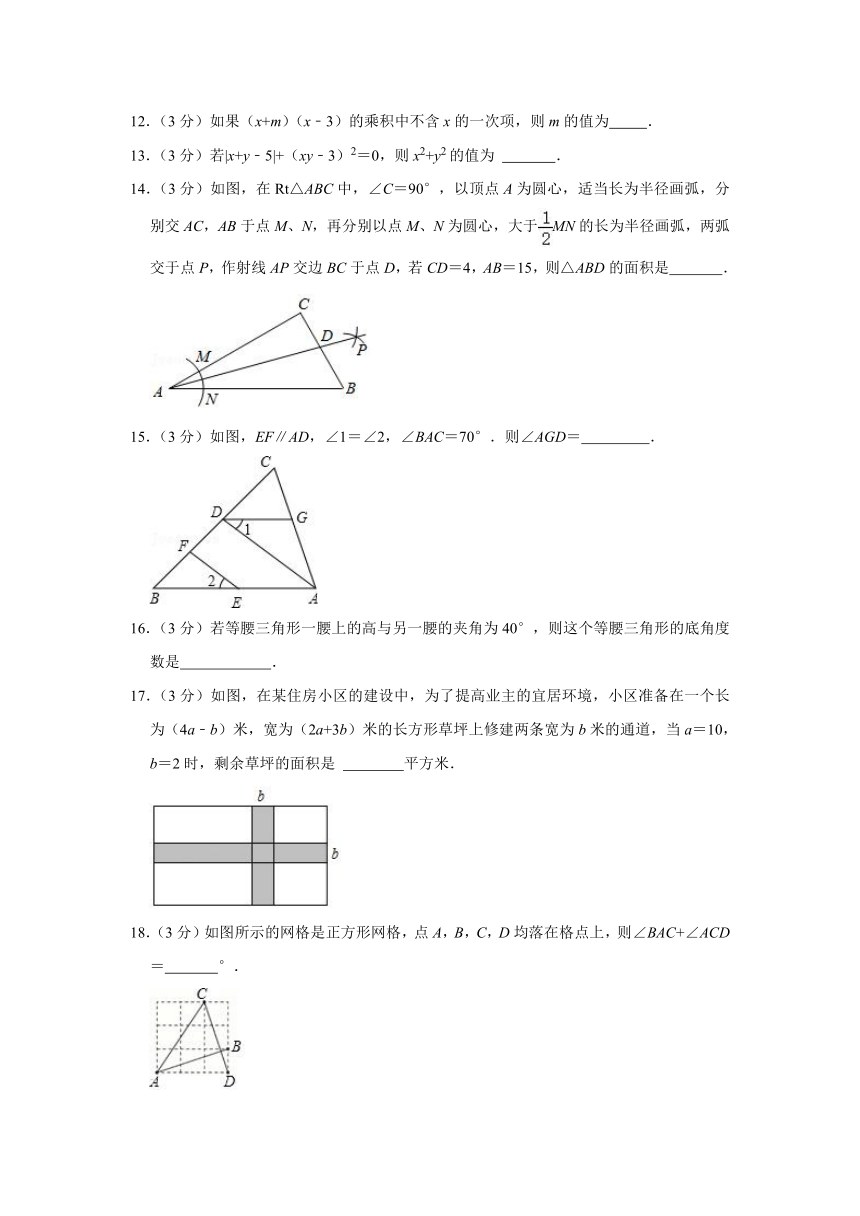
12.(3分)如果(x+m)(x﹣3)的乘积中不含x的一次项,则m的值为
.
13.(3分)若|x+y﹣5|+(xy﹣3)2=0,则x2+y2的值为
.
14.(3分)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是
.
15.(3分)如图,EF∥AD,∠1=∠2,∠BAC=70°.则∠AGD=
.
16.(3分)若等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的底角度数是
.
17.(3分)如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a﹣b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道,当a=10,b=2时,剩余草坪的面积是
平方米.
18.(3分)如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD=
°.
三、解答题(把解答或证明过程写在答题卡的相应区域内)
19.(5分)计算:(﹣)﹣3﹣(3.14﹣π)0﹣(0.125)2020×(﹣8)2021.
20.(7分)先化简,再求值.
[(a﹣2b)2+(a﹣2b)(2b+a)﹣2a(2a﹣b)]÷2a,其中a=,b=﹣2.
21.(7分)一个不透明的袋中装有5个黄球,13个黑球和22个红球,这些球除颜色外其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率为,则取出了多少个黑球?
22.(8分)如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
23.(9分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
24.(10分)(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?
2020-2021学年山东省菏泽市牡丹区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(木大题共10个小题,在每小题给出的四个选项中,只有一个选项是正确的,把正确选项的序号涂在答题卡的相应位置)
1.(3分)如图,四个图标分别是剑桥大学、北京理工大学、浙江大学和北京大学的校徽的重要组成部分,其中是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念判断即可.
【解答】解:A、不是轴对称图形;
B、不是轴对称图形;
C、不是轴对称图形;
D、是轴对称图形;
故选:D.
2.(3分)下列运算正确的是( )
A.(a+b)2=a2+b2
B.a3+3a3=4a3
C.(﹣2a2)3=6a6
D.(b+a)(a﹣b)=b2﹣a2
【分析】直接利用完全平方公式以及合并同类项法则、积的乘方运算法则、平方差公式分别化简得出答案.
【解答】解:A、(a+b)2=a2+2ab+b2,故此选项错误;
B、a3+3a3=4a3,正确;
C、(﹣2a2)3=﹣8a6,故此选项错误;
D、(b+a)(a﹣b)=﹣b2+a2,故此选项错误;
故选:B.
3.(3分)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
【分析】根据自变量、因变量的含义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【解答】解:∵在这个变化中,自变量是温度,因变量是声速,
∴选项A正确;
∵根据数据表,可得温度越高,声速越快,
∴选项B正确;
∵342×5=1710(m),
∴当空气温度为20℃时,声音5s可以传播1710m,
∴选项C错误;
∵324﹣318=6(m/s),330﹣324=6(m/s),336﹣330=6(m/s),342﹣336=6(m/s),348﹣342=6(m/s),
∴当温度每升高10℃,声速增加6m/s,
∴选项D正确.
故选:C.
4.(3分)下列说法中正确的个数有( )
①平面内,过一点有且只有一条直线与已知直线垂直;
②过一点有且只有一条直线与已知直线平行;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④如果两个角的两边分别平行,那么这两个角相等.
A.1个
B.2个
C.3个
D.4个
【分析】根据平行线的性质,垂线段定理,平行线,平行公理及推论,进行逐一判断即可.
【解答】解:①平面内,过一点有且只有一条直线与已知直线垂直,是真命题;
②过直线外一点有且只有一条直线与已知直线平行,原命题是假命题;
③连接直线外一点与直线上各点的所有线段中,垂线段最短,是真命题;
④如果两个角的两边分别平行,那么这两个角相等或互补,原命题是假命题;
故选:B.
5.(3分)如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40°
B.50°
C.60°
D.70°
【分析】依据平行线的性质,即可得到∠1=∠DFG=40°,再根据三角形外角性质,即可得到∠2的度数.
【解答】解:∵DF∥EG,
∴∠1=∠DFG=40°,
又∵∠A=30°,
∴∠2=∠A+∠DFG=30°+40°=70°,
故选:D.
6.(3分)如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )
A.40°
B.70°
C.30°
D.50°
【分析】根据等腰三角形的性质、三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到DA=DB,得到∠DBA=∠A=40°,计算即可.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵MN是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=40°,
∴∠DBC=30°,
故选:C.
7.(3分)如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
【分析】根据平行线的判定分别进行分析可得答案.
【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
8.(3分)如图,E、B、F、C四点在一条直线上,且EB=CF,∠A=∠D,增加下列条件中的一个仍不能证明△ABC≌△DEF,这个条件是( )
A.DF∥AC
B.AB=DE
C.∠E=∠ABC
D.AB∥DE
【分析】由EB=CF可求得EF=BC,结合∠A=∠D,根据全等三角形的判定方法,逐项判断即可.
【解答】解:
∵EB=CF,
∴EB+BF=BF+CF,即EF=BC,且∠A=∠D,
∴当DF∥AC时,可得∠DFE=∠C,满足AAS,可证明全等;
当AB=DE时,满足ASS,不能证明全等;
当∠E=∠ABC时,满足ASA,可证明全等;
当AB∥DE时,可得∠E=∠ABC,满足ASA,可证明全等;
故选:B.
9.(3分)甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟时两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
【分析】根据函数图象可以判断各选项是否正确,从而可以解答本题.
【解答】解:前2分钟,乙跑了300米,甲跑的路程小于300米,从而可知前2分钟,乙的平均速度比甲快,故选项A正确;
由图可知,5分钟时两人都跑了500米,故选项B正确;
由图可知,甲8分钟跑了800米,可得甲跑完800米的平均速度为100米/分,故选项C正确;
由图可得,甲8分钟跑了800米,乙8分钟跑了700米,故选项D错误;
故选:D.
10.(3分)如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.()n?75°
B.()n﹣1?65°
C.()n﹣1?75°
D.()n?85°
【分析】先根据等腰三角形的性质求出∠BA1C的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律即可得出第n个三角形中以An为顶点的底角度数.
【解答】解:∵在△CBA1中,∠B=30°,A1B=CB,
∴∠BA1C==75°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=∠BA1C=×75°;
同理可得,
∠EA3A2=()2×75°,∠FA4A3=()3×75°,
∴第n个三角形中以An为顶点的底角度数是()n﹣1×75°.
故选:C.
二、填空题(本大题共8个小题,只要求把最后结果填写在答题卡的相应区域内)
11.(3分)新型冠状病毒“COVID﹣19”的平均半径约为50纳米(1纳米=10﹣9米),这一数据用科学记数法表示为
5×10﹣8米 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:50纳米=50×10﹣9米=5×10﹣8米.
故答案为:5×10﹣8米.
12.(3分)如果(x+m)(x﹣3)的乘积中不含x的一次项,则m的值为 3 .
【分析】把式子展开,找到所有x的一次项的所有系数,令其为0,可求出m的值.
【解答】解:∵(x+m)(x﹣3)=x2﹣3x+mx﹣3m=x2+(m﹣3)x﹣3m,
又∵结果中不含x的一次项,
∴m﹣3=0,解得m=3.
故答案为:3.
13.(3分)若|x+y﹣5|+(xy﹣3)2=0,则x2+y2的值为
19 .
【分析】根据偶次方、绝对值的非负性求出x+y=5,xy=3,进而利用x2+y2=(x+y)2﹣2xy求出结果即可.
【解答】解:∵|x+y﹣5|+(xy﹣3)2=0,
又∵|x+y﹣5|≥0,(xy﹣3)2≥0,
∴x+y﹣5=0,xy﹣3=0,
∴x+y=5,xy=3,
∴x2+y2=(x+y)2﹣2xy
=52﹣2×3
=19,
故答案为:19.
14.(3分)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是 30 .
【分析】根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=30,
故答案为:30.
15.(3分)如图,EF∥AD,∠1=∠2,∠BAC=70°.则∠AGD= 110° .
【分析】由EF∥AD,根据两直线平行,同位角相等,即可得∠2=∠BAD,又由∠1=∠2,根据内错角相等,两直线平行,易证得DG∥AB,然后根据两直线平行,同旁内角互补,即可求得∠AGD的度数.
【解答】解:∵EF∥AD,
∴∠BAD=∠2,
∵∠1=∠2,
∴∠1=∠BAD,
∴DG∥AB,
∴∠BAC+∠AGD=180°,
∵∠BAC=70°,
∴∠AGD=110°.
故答案为:110°.
16.(3分)若等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的底角度数是 65°或25° .
【分析】在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,讨论:当BD在△ABC内部时,如图1,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形内角和可计算出∠ACB;当BD在△ABC外部时,如图2,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形外角性质可计算出∠ACB.
【解答】解:在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,
当BD在△ABC内部时,如图1,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣40°=50°,
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣50°)=65°;
当BD在△ABC外部时,如图2,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣40°=50°,
∵AB=AC,
∴∠ABC=∠ACB,
而∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=25°,
综上所述,这个等腰三角形底角的度数为65°或25°.
故答案为:65°或25°.
17.(3分)如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a﹣b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道,当a=10,b=2时,剩余草坪的面积是
864 平方米.
【分析】根据剩余草坪的面积=大长方形面积﹣通道的面积计算即可.
【解答】解:由题意可得:
(4a﹣b﹣b)(2a+3b﹣b)
=4(2a﹣b)(a+b)
=4(2a2+2ab﹣ab﹣b2)
=8a2+4ab﹣4b2;
a=10,b=2时,
原式=8×102+4×10×2﹣4×22
=800+80﹣16
=864(平方米),
故答案为:864.
18.(3分)如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD= 90 °.
【分析】证明△DCE≌△ABD(SAS),得∠CDE=∠DAB,根据同角的余角相等和三角形的内角和可得结论.
【解答】解:在△DCE和△ABD中,
∵,
∴△DCE≌△ABD(SAS),
∴∠CDE=∠DAB,
∵∠CDE+∠ADC=∠ADC+∠DAB=90°,
∴∠AFD=90°,
∴∠BAC+∠ACD=90°,
故答案为:90.
三、解答题(把解答或证明过程写在答题卡的相应区域内)
19.(5分)计算:(﹣)﹣3﹣(3.14﹣π)0﹣(0.125)2020×(﹣8)2021.
【分析】负整数指数幂:a﹣p=;任何非零数的零次幂等于1;积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘.据此计算即可.
【解答】解:原式=
=﹣8﹣1﹣(﹣1)2020×(﹣8)
=﹣8﹣1﹣1×(﹣8)
=﹣8﹣1+8
=﹣1.
20.(7分)先化简,再求值.
[(a﹣2b)2+(a﹣2b)(2b+a)﹣2a(2a﹣b)]÷2a,其中a=,b=﹣2.
【分析】先根据完全平方公式,平方差公式,单项式乘多项式进行计算,再合并同类项,算除法,最后代入求出答案即可
【解答】解:原式=[a2﹣4ab+4b2+a2﹣4b2﹣(4a2﹣2ab)]÷2a=
(a2﹣4ab+4b2+a2﹣4b2﹣4a2+2ab)÷2a
=(2a2﹣4ab﹣4a2+2ab)÷2a
=(﹣2a2﹣2ab)÷2a
=﹣a﹣b,
当,b=﹣2时,原式=.
21.(7分)一个不透明的袋中装有5个黄球,13个黑球和22个红球,这些球除颜色外其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率为,则取出了多少个黑球?
【分析】(1)用黄球的个数除以球的总个数即可得;
(2)用不是红球的个数,即黄球和黑球的个数除以总个数即可得;
(3)设取出了x个黑球,用变化后黄球的数量÷总数量=摸出一个球是黄球的概率列出方程,解之可得.
【解答】解:(1)因为共有5+13+22=40个小球,
所以从袋中摸出一个球是黄球的概率为=;
(2)从袋中摸出一个球不是红球的概率为=;
(3)设取出了x个黑球,
根据题意,得:=,
解得:x=11,
答:取出了11个黑球.
22.(8分)如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
【分析】(1)根据平行线的性质和判定定理即可得到结论;
(2)首先根据O是CD的中点,可得DO=CO,再证明∠D=∠OCE,然后可利用ASA定理证明△AOD≌△EOC.
【解答】解:(1)AD∥BE,
理由:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
23.(9分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
【分析】(1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,可得答案;
(3)根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案;
(4)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得速度.
【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据题意,小明在书店停留的时间为从(8分)到(12分),
故小明在书店停留了4分钟.
(3)一共行驶的总路程=1200+(1200﹣600)+(1500﹣600)
=1200+600+900=2700米;
共用了14分钟.
(4)由图象可知:0~6分钟时,平均速度==200米/分,
6~8分钟时,平均速度==300米/分,
12~14分钟时,平均速度==450米/分,
所以,12~14分钟时速度最快,不在安全限度内.
24.(10分)(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?
【分析】(1)只要证明△ABE≌△ADC即可解决问题;
(2)根据等边三角形的性质得出AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE,根据全等三角形的性质得出∠BEA=∠ACD,求出∠BOC=∠ECO+∠OEC=∠ACE+∠AEC,代入求出即可;
【解答】(1)证明:∵△ABD和△ACE都是等腰直角三角形(已知)
∴AB=AD,AE=AC(等腰直角三角形定义)
又∵∠BAD=∠CAE=90°(已知)
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAC,
∴△ABE≌△ADC
∴BE=DC(全等三角形的对应边相等)
∠ABE=∠ADC(全等三角形的对应角相等)
又∵∠BFO=∠DFA,∠ADF+∠DFA=90°(直角三角形的两个锐角互余)
∴∠ABE+∠BFO=90°(等量代换)
∴∠BOF=∠DAF=90,
即BE⊥DC.
(2)解:结论:BE=CD.
理由:如图2,∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=BE,∠BEA=∠ACD,
∴∠BOC=∠ECO+∠OEC
=∠DCA+∠ACE+∠OEC
=∠BEA+∠ACE+∠OEC
=∠ACE+∠AEC
=60°+60°
=120°.
∴∠BOD=60°.
一、选择题(木大题共10个小题,在每小题给出的四个选项中,只有一个选项是正确的,把正确选项的序号涂在答题卡的相应位置)
1.(3分)如图,四个图标分别是剑桥大学、北京理工大学、浙江大学和北京大学的校徽的重要组成部分,其中是轴对称图形的是( )
A.
B.
C.
D.
2.(3分)下列运算正确的是( )
A.(a+b)2=a2+b2
B.a3+3a3=4a3
C.(﹣2a2)3=6a6
D.(b+a)(a﹣b)=b2﹣a2
3.(3分)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
4.(3分)下列说法中正确的个数有( )
①平面内,过一点有且只有一条直线与已知直线垂直;
②过一点有且只有一条直线与已知直线平行;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④如果两个角的两边分别平行,那么这两个角相等.
A.1个
B.2个
C.3个
D.4个
5.(3分)如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40°
B.50°
C.60°
D.70°
6.(3分)如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )
A.40°
B.70°
C.30°
D.50°
7.(3分)如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
8.(3分)如图,E、B、F、C四点在一条直线上,且EB=CF,∠A=∠D,增加下列条件中的一个仍不能证明△ABC≌△DEF,这个条件是( )
A.DF∥AC
B.AB=DE
C.∠E=∠ABC
D.AB∥DE
9.(3分)甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟时两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
10.(3分)如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.()n?75°
B.()n﹣1?65°
C.()n﹣1?75°
D.()n?85°
二、填空题(本大题共8个小题,只要求把最后结果填写在答题卡的相应区域内)
11.(3分)新型冠状病毒“COVID﹣19”的平均半径约为50纳米(1纳米=10﹣9米),这一数据用科学记数法表示为
.
12.(3分)如果(x+m)(x﹣3)的乘积中不含x的一次项,则m的值为
.
13.(3分)若|x+y﹣5|+(xy﹣3)2=0,则x2+y2的值为
.
14.(3分)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是
.
15.(3分)如图,EF∥AD,∠1=∠2,∠BAC=70°.则∠AGD=
.
16.(3分)若等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的底角度数是
.
17.(3分)如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a﹣b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道,当a=10,b=2时,剩余草坪的面积是
平方米.
18.(3分)如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD=
°.
三、解答题(把解答或证明过程写在答题卡的相应区域内)
19.(5分)计算:(﹣)﹣3﹣(3.14﹣π)0﹣(0.125)2020×(﹣8)2021.
20.(7分)先化简,再求值.
[(a﹣2b)2+(a﹣2b)(2b+a)﹣2a(2a﹣b)]÷2a,其中a=,b=﹣2.
21.(7分)一个不透明的袋中装有5个黄球,13个黑球和22个红球,这些球除颜色外其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率为,则取出了多少个黑球?
22.(8分)如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
23.(9分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
24.(10分)(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?
2020-2021学年山东省菏泽市牡丹区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(木大题共10个小题,在每小题给出的四个选项中,只有一个选项是正确的,把正确选项的序号涂在答题卡的相应位置)
1.(3分)如图,四个图标分别是剑桥大学、北京理工大学、浙江大学和北京大学的校徽的重要组成部分,其中是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念判断即可.
【解答】解:A、不是轴对称图形;
B、不是轴对称图形;
C、不是轴对称图形;
D、是轴对称图形;
故选:D.
2.(3分)下列运算正确的是( )
A.(a+b)2=a2+b2
B.a3+3a3=4a3
C.(﹣2a2)3=6a6
D.(b+a)(a﹣b)=b2﹣a2
【分析】直接利用完全平方公式以及合并同类项法则、积的乘方运算法则、平方差公式分别化简得出答案.
【解答】解:A、(a+b)2=a2+2ab+b2,故此选项错误;
B、a3+3a3=4a3,正确;
C、(﹣2a2)3=﹣8a6,故此选项错误;
D、(b+a)(a﹣b)=﹣b2+a2,故此选项错误;
故选:B.
3.(3分)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
【分析】根据自变量、因变量的含义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【解答】解:∵在这个变化中,自变量是温度,因变量是声速,
∴选项A正确;
∵根据数据表,可得温度越高,声速越快,
∴选项B正确;
∵342×5=1710(m),
∴当空气温度为20℃时,声音5s可以传播1710m,
∴选项C错误;
∵324﹣318=6(m/s),330﹣324=6(m/s),336﹣330=6(m/s),342﹣336=6(m/s),348﹣342=6(m/s),
∴当温度每升高10℃,声速增加6m/s,
∴选项D正确.
故选:C.
4.(3分)下列说法中正确的个数有( )
①平面内,过一点有且只有一条直线与已知直线垂直;
②过一点有且只有一条直线与已知直线平行;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④如果两个角的两边分别平行,那么这两个角相等.
A.1个
B.2个
C.3个
D.4个
【分析】根据平行线的性质,垂线段定理,平行线,平行公理及推论,进行逐一判断即可.
【解答】解:①平面内,过一点有且只有一条直线与已知直线垂直,是真命题;
②过直线外一点有且只有一条直线与已知直线平行,原命题是假命题;
③连接直线外一点与直线上各点的所有线段中,垂线段最短,是真命题;
④如果两个角的两边分别平行,那么这两个角相等或互补,原命题是假命题;
故选:B.
5.(3分)如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40°
B.50°
C.60°
D.70°
【分析】依据平行线的性质,即可得到∠1=∠DFG=40°,再根据三角形外角性质,即可得到∠2的度数.
【解答】解:∵DF∥EG,
∴∠1=∠DFG=40°,
又∵∠A=30°,
∴∠2=∠A+∠DFG=30°+40°=70°,
故选:D.
6.(3分)如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )
A.40°
B.70°
C.30°
D.50°
【分析】根据等腰三角形的性质、三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到DA=DB,得到∠DBA=∠A=40°,计算即可.
【解答】解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵MN是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=40°,
∴∠DBC=30°,
故选:C.
7.(3分)如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
【分析】根据平行线的判定分别进行分析可得答案.
【解答】解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
8.(3分)如图,E、B、F、C四点在一条直线上,且EB=CF,∠A=∠D,增加下列条件中的一个仍不能证明△ABC≌△DEF,这个条件是( )
A.DF∥AC
B.AB=DE
C.∠E=∠ABC
D.AB∥DE
【分析】由EB=CF可求得EF=BC,结合∠A=∠D,根据全等三角形的判定方法,逐项判断即可.
【解答】解:
∵EB=CF,
∴EB+BF=BF+CF,即EF=BC,且∠A=∠D,
∴当DF∥AC时,可得∠DFE=∠C,满足AAS,可证明全等;
当AB=DE时,满足ASS,不能证明全等;
当∠E=∠ABC时,满足ASA,可证明全等;
当AB∥DE时,可得∠E=∠ABC,满足ASA,可证明全等;
故选:B.
9.(3分)甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟时两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
【分析】根据函数图象可以判断各选项是否正确,从而可以解答本题.
【解答】解:前2分钟,乙跑了300米,甲跑的路程小于300米,从而可知前2分钟,乙的平均速度比甲快,故选项A正确;
由图可知,5分钟时两人都跑了500米,故选项B正确;
由图可知,甲8分钟跑了800米,可得甲跑完800米的平均速度为100米/分,故选项C正确;
由图可得,甲8分钟跑了800米,乙8分钟跑了700米,故选项D错误;
故选:D.
10.(3分)如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
A.()n?75°
B.()n﹣1?65°
C.()n﹣1?75°
D.()n?85°
【分析】先根据等腰三角形的性质求出∠BA1C的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律即可得出第n个三角形中以An为顶点的底角度数.
【解答】解:∵在△CBA1中,∠B=30°,A1B=CB,
∴∠BA1C==75°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=∠BA1C=×75°;
同理可得,
∠EA3A2=()2×75°,∠FA4A3=()3×75°,
∴第n个三角形中以An为顶点的底角度数是()n﹣1×75°.
故选:C.
二、填空题(本大题共8个小题,只要求把最后结果填写在答题卡的相应区域内)
11.(3分)新型冠状病毒“COVID﹣19”的平均半径约为50纳米(1纳米=10﹣9米),这一数据用科学记数法表示为
5×10﹣8米 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:50纳米=50×10﹣9米=5×10﹣8米.
故答案为:5×10﹣8米.
12.(3分)如果(x+m)(x﹣3)的乘积中不含x的一次项,则m的值为 3 .
【分析】把式子展开,找到所有x的一次项的所有系数,令其为0,可求出m的值.
【解答】解:∵(x+m)(x﹣3)=x2﹣3x+mx﹣3m=x2+(m﹣3)x﹣3m,
又∵结果中不含x的一次项,
∴m﹣3=0,解得m=3.
故答案为:3.
13.(3分)若|x+y﹣5|+(xy﹣3)2=0,则x2+y2的值为
19 .
【分析】根据偶次方、绝对值的非负性求出x+y=5,xy=3,进而利用x2+y2=(x+y)2﹣2xy求出结果即可.
【解答】解:∵|x+y﹣5|+(xy﹣3)2=0,
又∵|x+y﹣5|≥0,(xy﹣3)2≥0,
∴x+y﹣5=0,xy﹣3=0,
∴x+y=5,xy=3,
∴x2+y2=(x+y)2﹣2xy
=52﹣2×3
=19,
故答案为:19.
14.(3分)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是 30 .
【分析】根据角平分线的性质得到DE=DC=4,根据三角形的面积公式计算即可.
【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=30,
故答案为:30.
15.(3分)如图,EF∥AD,∠1=∠2,∠BAC=70°.则∠AGD= 110° .
【分析】由EF∥AD,根据两直线平行,同位角相等,即可得∠2=∠BAD,又由∠1=∠2,根据内错角相等,两直线平行,易证得DG∥AB,然后根据两直线平行,同旁内角互补,即可求得∠AGD的度数.
【解答】解:∵EF∥AD,
∴∠BAD=∠2,
∵∠1=∠2,
∴∠1=∠BAD,
∴DG∥AB,
∴∠BAC+∠AGD=180°,
∵∠BAC=70°,
∴∠AGD=110°.
故答案为:110°.
16.(3分)若等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的底角度数是 65°或25° .
【分析】在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,讨论:当BD在△ABC内部时,如图1,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形内角和可计算出∠ACB;当BD在△ABC外部时,如图2,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形外角性质可计算出∠ACB.
【解答】解:在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,
当BD在△ABC内部时,如图1,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣40°=50°,
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣50°)=65°;
当BD在△ABC外部时,如图2,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°﹣40°=50°,
∵AB=AC,
∴∠ABC=∠ACB,
而∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=25°,
综上所述,这个等腰三角形底角的度数为65°或25°.
故答案为:65°或25°.
17.(3分)如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a﹣b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道,当a=10,b=2时,剩余草坪的面积是
864 平方米.
【分析】根据剩余草坪的面积=大长方形面积﹣通道的面积计算即可.
【解答】解:由题意可得:
(4a﹣b﹣b)(2a+3b﹣b)
=4(2a﹣b)(a+b)
=4(2a2+2ab﹣ab﹣b2)
=8a2+4ab﹣4b2;
a=10,b=2时,
原式=8×102+4×10×2﹣4×22
=800+80﹣16
=864(平方米),
故答案为:864.
18.(3分)如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD= 90 °.
【分析】证明△DCE≌△ABD(SAS),得∠CDE=∠DAB,根据同角的余角相等和三角形的内角和可得结论.
【解答】解:在△DCE和△ABD中,
∵,
∴△DCE≌△ABD(SAS),
∴∠CDE=∠DAB,
∵∠CDE+∠ADC=∠ADC+∠DAB=90°,
∴∠AFD=90°,
∴∠BAC+∠ACD=90°,
故答案为:90.
三、解答题(把解答或证明过程写在答题卡的相应区域内)
19.(5分)计算:(﹣)﹣3﹣(3.14﹣π)0﹣(0.125)2020×(﹣8)2021.
【分析】负整数指数幂:a﹣p=;任何非零数的零次幂等于1;积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘.据此计算即可.
【解答】解:原式=
=﹣8﹣1﹣(﹣1)2020×(﹣8)
=﹣8﹣1﹣1×(﹣8)
=﹣8﹣1+8
=﹣1.
20.(7分)先化简,再求值.
[(a﹣2b)2+(a﹣2b)(2b+a)﹣2a(2a﹣b)]÷2a,其中a=,b=﹣2.
【分析】先根据完全平方公式,平方差公式,单项式乘多项式进行计算,再合并同类项,算除法,最后代入求出答案即可
【解答】解:原式=[a2﹣4ab+4b2+a2﹣4b2﹣(4a2﹣2ab)]÷2a=
(a2﹣4ab+4b2+a2﹣4b2﹣4a2+2ab)÷2a
=(2a2﹣4ab﹣4a2+2ab)÷2a
=(﹣2a2﹣2ab)÷2a
=﹣a﹣b,
当,b=﹣2时,原式=.
21.(7分)一个不透明的袋中装有5个黄球,13个黑球和22个红球,这些球除颜色外其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率为,则取出了多少个黑球?
【分析】(1)用黄球的个数除以球的总个数即可得;
(2)用不是红球的个数,即黄球和黑球的个数除以总个数即可得;
(3)设取出了x个黑球,用变化后黄球的数量÷总数量=摸出一个球是黄球的概率列出方程,解之可得.
【解答】解:(1)因为共有5+13+22=40个小球,
所以从袋中摸出一个球是黄球的概率为=;
(2)从袋中摸出一个球不是红球的概率为=;
(3)设取出了x个黑球,
根据题意,得:=,
解得:x=11,
答:取出了11个黑球.
22.(8分)如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)试判断AD与BE有怎样的位置关系,并说明理由;
(2)试说明△AOD≌△EOC.
【分析】(1)根据平行线的性质和判定定理即可得到结论;
(2)首先根据O是CD的中点,可得DO=CO,再证明∠D=∠OCE,然后可利用ASA定理证明△AOD≌△EOC.
【解答】解:(1)AD∥BE,
理由:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
∴△AOD≌△EOC(ASA).
23.(9分)“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
【分析】(1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,可得答案;
(3)根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案;
(4)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得速度.
【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
(2)根据题意,小明在书店停留的时间为从(8分)到(12分),
故小明在书店停留了4分钟.
(3)一共行驶的总路程=1200+(1200﹣600)+(1500﹣600)
=1200+600+900=2700米;
共用了14分钟.
(4)由图象可知:0~6分钟时,平均速度==200米/分,
6~8分钟时,平均速度==300米/分,
12~14分钟时,平均速度==450米/分,
所以,12~14分钟时速度最快,不在安全限度内.
24.(10分)(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?
【分析】(1)只要证明△ABE≌△ADC即可解决问题;
(2)根据等边三角形的性质得出AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE,根据全等三角形的性质得出∠BEA=∠ACD,求出∠BOC=∠ECO+∠OEC=∠ACE+∠AEC,代入求出即可;
【解答】(1)证明:∵△ABD和△ACE都是等腰直角三角形(已知)
∴AB=AD,AE=AC(等腰直角三角形定义)
又∵∠BAD=∠CAE=90°(已知)
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAC,
∴△ABE≌△ADC
∴BE=DC(全等三角形的对应边相等)
∠ABE=∠ADC(全等三角形的对应角相等)
又∵∠BFO=∠DFA,∠ADF+∠DFA=90°(直角三角形的两个锐角互余)
∴∠ABE+∠BFO=90°(等量代换)
∴∠BOF=∠DAF=90,
即BE⊥DC.
(2)解:结论:BE=CD.
理由:如图2,∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=BE,∠BEA=∠ACD,
∴∠BOC=∠ECO+∠OEC
=∠DCA+∠ACE+∠OEC
=∠BEA+∠ACE+∠OEC
=∠ACE+∠AEC
=60°+60°
=120°.
∴∠BOD=60°.
同课章节目录
