山东济宁任城2020-2021鲁教版五四制数学九年级下册期末达标检测卷(word含答案)
文档属性
| 名称 | 山东济宁任城2020-2021鲁教版五四制数学九年级下册期末达标检测卷(word含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览





文档简介
期末达标检测卷
一、选择题(每题3分,共30分)
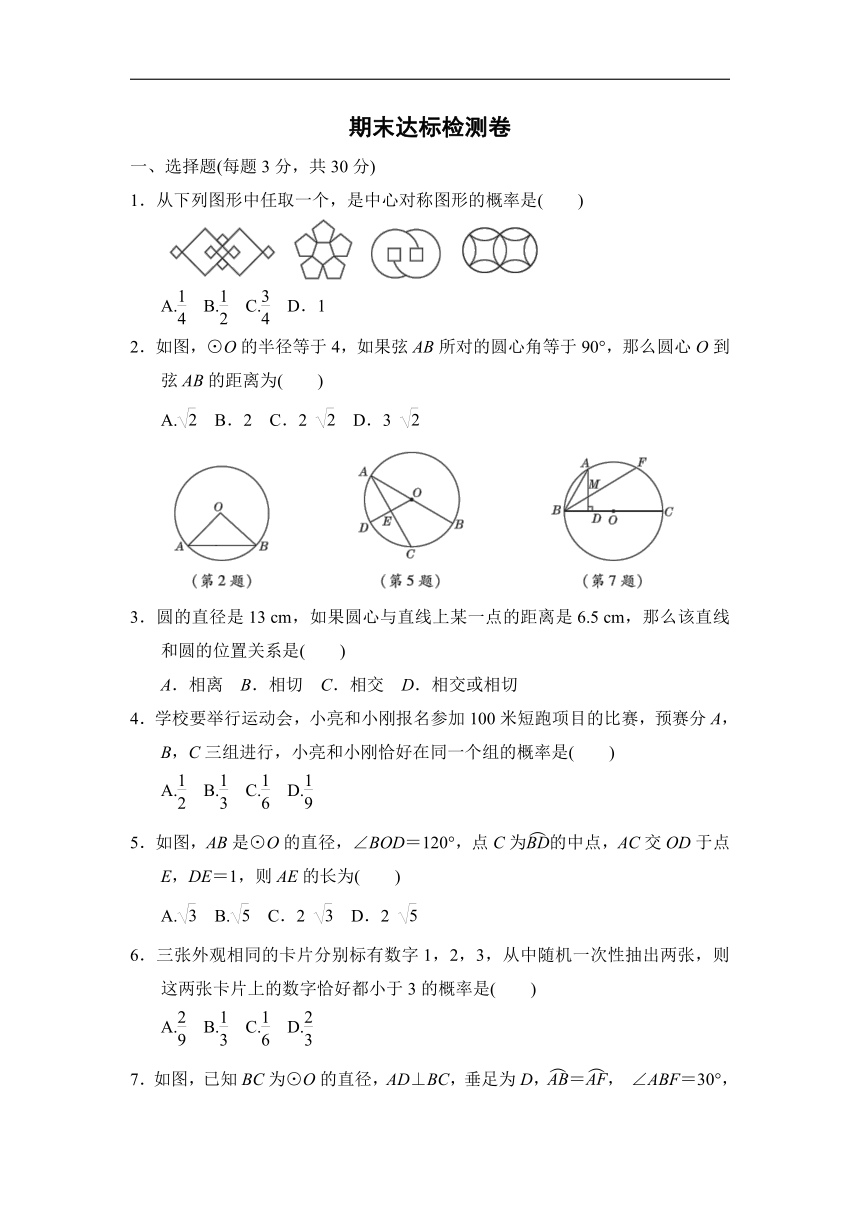
1.从下列图形中任取一个,是中心对称图形的概率是( )
A.
B.
C.
D.1
2.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A.
B.2
C.2
D.3
3.圆的直径是13
cm,如果圆心与直线上某一点的距离是6.5
cm,那么该直线和圆的位置关系是( )
A.相离
B.相切
C.相交
D.相交或相切
4.学校要举行运动会,小亮和小刚报名参加100米短跑项目的比赛,预赛分A,B,C三组进行,小亮和小刚恰好在同一个组的概率是( )
A.
B.
C.
D.
5.如图,AB是⊙O的直径,∠BOD=120°,点C为的中点,AC交OD于点E,DE=1,则AE的长为( )
A.
B.
C.2
D.2
6.三张外观相同的卡片分别标有数字1,2,3,从中随机一次性抽出两张,则这两张卡片上的数字恰好都小于3的概率是( )
A.
B.
C.
D.
7.如图,已知BC为⊙O的直径,AD⊥BC,垂足为D,=,
∠ABF=30°,则∠BAD等于( )
A.
30°
B.
45°
C.
60°
D.
22.5°
8.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60°
B.90°
C.120°
D.180°
9.如图,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动地在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径与x轴围成的面积为( )
A.+
B.
+1
C.
π+1
D.
π+
10.如图,抛物线过点A(2,0),B(6,0),C,平行于x轴的直线CD交抛物线于点C,D,以AB为直径的圆交直线CD于点E,F,则CE+FD的值是( )
A.
2
B.
4
C.
3
D.
6
二、填空题(每题3分,共24分)
11.如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为________.
12.某批篮球的质量检验结果如下:
抽取的篮球数n
100
200
400
600
800
1
000
1
200
优等品的频数m
93
192
380
561
752
941
1
128
优等品的频率
0.930
0.960
0.950
0.935
0.940
0.941
0.940
从这批篮球中,任意抽取一个篮球是优等品的概率的估计值是________.(精确到0.01)
13.如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为________.
14.如图,在△ABC中,AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,则CD的长为________.
15.对于四边形ABCD,有四个条件:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从中任选两个作为已知条件,能判定四边形ABCD是平行四边形的概率是________.
16.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于________.
17.从-2,0,2这三个数中,任取两个不同的数分别作为a,b的值,恰好使得关于x的方程x2+ax-b=0有实数解的概率为________.
18.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2
cm的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为________cm2.(圆周率用π表示)
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A=66°,求∠ADB的度数.
20.在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球试验,他们将30个与红球大小完全相同的白球装入试验袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次试验汇总后统计的数据:
摸球的次数s
150
200
500
900
1
000
1
200
摸到白球的频数n
51
64
156
275
303
361
摸到白球的频率
0.34
0.32
0.312
0.306
0.303
0.301
(1)请估计:当次数s很大时,摸到白球的频率将会接近________;假如你去摸一次,你摸到红球的概率是________(精确到0.1).
(2)试估算口袋中红球有多少个?
21.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠B=30°,AB=8,求DE的长.
22.有两个可以自由转动的均匀转盘,都被分成了3等份,并在每一份内标有数字,如图,规则如下:
①分别转动转盘A,B;②两个转盘停止后观察两个指针所指的数字(若指针指在等分线上,则重转一次,直到指针指向某一数字为止).
(1)用列表法分别求出“两个指针所指的数字都是方程x2-5x+6=0的解”的概率和“两个指针所指的数字都不是方程x2-5x+6=0的解”的概率;
(2)王磊和张浩想用这两个转盘做游戏,他们规定:“若两个指针所指的数字都是x2-5x+6=0的解”时,王磊得1分;若“两个指针所指的数字都不是x2-5x+6=0的解”时,张浩得3分,这个游戏公平吗?若你认为不公平,请修改得分规定,使游戏对双方公平.
23.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
24.图①和图②中,优弧AB所在⊙O的半径为2,AB=2
.点P为优弧AB上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是________,当BP经过点O时,∠ABA′=________;
(2)当BA′与⊙O相切时,如图②,求折痕BP的长;
(3)若线段BA′与优弧AB只有一个公共点B,设∠ABP=α,确定α的取值范围.
答案
一、1.C 2.C 3.D 4.B
5.A 点拨:如图,连接OC.
∵∠DOB=120°,
∴∠AOD=60°.
∵=,
∴∠DOC=∠BOC=60°,
∴∠AOD=∠DOC,
∴=,
∴OD⊥AC,
∴∠A=30°.
设OA=r,则OE=r=DE=1,
∴r=2,即OA=2,
∴AE==.
6.B 7.A 8.C
9.C 点拨:如图,点A运动的路径与x轴围成的面积为S1+S2+S3+S4+S5=+++2×=π+1.故选C.
10.B 点拨:如图,∵点A,B的坐标分别是(2,0),(6,0),
∴AB的中点M的坐标为(4,0),且点M是圆心,
作MN⊥CD于点N,则EN=FN,
又由抛物线的对称性可知CN=DN,
∴CE=DF.连接EM.
在Rt△EMN中,EN====1.
又CN=4-1=3,
∴CE=CN-EN=3-1=2,
∴CE+DF=2+2=4.
二、11. 12.0.94
13.75°
点拨:如图,连接DO,FO,
∵在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°.
∵内切圆O与边AB,BC,CA分别相切于点D,E,F,
∴∠ODA=∠OFA=90°,
∴∠DOF=150°,
∴∠DEF=∠DOF=75°.
14. 点拨:如图,过点A作AE⊥BD于点E,连接AD,
∴AD=AB=5,
根据垂径定理,得DE=BE,
∴CE=BE-BC=DE-2,
根据勾股定理,得AD2-DE2=AC2-CE2,
∴52-DE2=42-(DE-2)2,
解得DE=,
∴CD=DE+CE=2DE-2=.
15. 16.54° 17.
18.(2π-2
) 点拨:如图,过A作AD⊥BC于D.
由题意得AB=AC=BC=2
cm,∠BAC=∠ABC=∠ACB=60°,
∴AD=AB·sin
60°=2×=(cm),
∴△ABC的面积=BC·AD=
cm2,
S扇形BAC==π(cm2),
∴“莱洛三角形”的面积=3×π-2×=2π-2
(cm2).
三、19.(1)证明:∵DB平分∠ADC,
∴=.
∵OC⊥BD,
∴=,
∴=,
∴AB=CD.
(2)解:∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°-∠A=114°.
∵=,
∴BC=CD,
∴∠BDC=×(180°-114°)=33°.
∵DB平分∠ADC,
∴∠ADB=∠BDC=33°.
20.解:(1)0.3;0.7
(2)设口袋中红球有x个,
由题意得0.7=,
解得x=70,
经检验x=70是原方程的解.
∴估计口袋中红球有70个.
21.(1)证明:如图,连接OD,
则OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C.
∴∠ODB=∠C.
∴OD∥AC.
∴∠ODE=∠DEC=90°.
∴DE是⊙O的切线.
(2)解:如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴BD=AB·cos
B=8×=4
.
又∵AB=AC,
∴CD=BD=4
,∠C=∠B=30°.
∴DE=CD=2
.
22.解:(1)解方程x2-5x+6=0,
得x1=2,x2=3,列表如下:
2
3
4
1
1,2
1,3
1,4
2
2,2
2,3
2,4
3
3,2
3,3
3,4
由表知,两个指针所指的数字都是该方程的解的概率是,两个指针所指的数字都不是该方程的解的概率是.
(2)因为1×≠3×,所以游戏不公平.
修改得分规定为:若两个指针所指的数字都是x2-5x+6=0的解时,王磊得1分;若两个指针所指的数字都不是x2-5x+6=0的解时,张浩得4分.(修改得分规定不唯一)
23.(1)证明:如图,连接OC.
∵AD⊥EF,
∴∠ADC=90°.
∴∠ACD+∠CAD=90°.
∵OC=OA,
∴∠ACO=∠CAO.
∵∠DAC=∠BAC,
∴∠ACD+∠ACO=90°,
即∠OCD=90°.
∴EF是⊙O的切线.
(2)证明:如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠ADC=90°=∠ACB.
∵∠DAC=∠BAC,
∴△ACD∽△ABC.
∴=,
即AC2=AD·AB.
(3)解:∵∠OCD=90°,
∠ACD=30°,
∴∠OCA=60°.
∵OC=OA,
∴△ACO是等边三角形.
∴AC=OC=2,∠AOC=60°.
在Rt△ADC中,
∵∠ACD=30°,
∴AD=1,CD=.
∴S阴影=S梯形OCDA-S扇形OCA=(1+2)×-=-.
24.解:(1)1;60°
(2)如图,作OC⊥AB于点C,
连接OB.
∵BA′与⊙O相切,
∴∠OBA′=90°.
在Rt△OBC中,
∵OB=2,OC=1,
∴sin
∠OBC==.
∴∠OBC=30°.
∴∠ABP=∠ABA′=
(∠OBA′+∠OBC)=60°.
∴∠OBP=30°.
作OD⊥BP于点D,则BP=2BD.
∵BD=OB·cos
30°=,
∴BP=2
.
(3)∵点P,A不重合,
∴α>0°.
由(1)得,当α增大到30°时,点A′在优弧AB上,
∴当0°<α<30°时,点A′在⊙O内,线段BA′与优弧AB只有一个公共点B.
由(2)知,α增大到60°时,BA′与⊙O相切,即线段BA′与优弧AB只有一个公共点B.
当α继续增大时,点P逐渐靠近点B,但点P,B不重合,
∴∠OBP<90°.
∵α=∠OBA+∠OBP,∠OBA=30°,
∴α<120°.
∴当60°≤α<120°时,线段BA′与优弧AB只有一个公共点B.
综上所述,α的取值范围是0°<α<30°或60°≤α<120°.
一、选择题(每题3分,共30分)
1.从下列图形中任取一个,是中心对称图形的概率是( )
A.
B.
C.
D.1
2.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于90°,那么圆心O到弦AB的距离为( )
A.
B.2
C.2
D.3
3.圆的直径是13
cm,如果圆心与直线上某一点的距离是6.5
cm,那么该直线和圆的位置关系是( )
A.相离
B.相切
C.相交
D.相交或相切
4.学校要举行运动会,小亮和小刚报名参加100米短跑项目的比赛,预赛分A,B,C三组进行,小亮和小刚恰好在同一个组的概率是( )
A.
B.
C.
D.
5.如图,AB是⊙O的直径,∠BOD=120°,点C为的中点,AC交OD于点E,DE=1,则AE的长为( )
A.
B.
C.2
D.2
6.三张外观相同的卡片分别标有数字1,2,3,从中随机一次性抽出两张,则这两张卡片上的数字恰好都小于3的概率是( )
A.
B.
C.
D.
7.如图,已知BC为⊙O的直径,AD⊥BC,垂足为D,=,
∠ABF=30°,则∠BAD等于( )
A.
30°
B.
45°
C.
60°
D.
22.5°
8.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
A.60°
B.90°
C.120°
D.180°
9.如图,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动地在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径与x轴围成的面积为( )
A.+
B.
+1
C.
π+1
D.
π+
10.如图,抛物线过点A(2,0),B(6,0),C,平行于x轴的直线CD交抛物线于点C,D,以AB为直径的圆交直线CD于点E,F,则CE+FD的值是( )
A.
2
B.
4
C.
3
D.
6
二、填空题(每题3分,共24分)
11.如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为________.
12.某批篮球的质量检验结果如下:
抽取的篮球数n
100
200
400
600
800
1
000
1
200
优等品的频数m
93
192
380
561
752
941
1
128
优等品的频率
0.930
0.960
0.950
0.935
0.940
0.941
0.940
从这批篮球中,任意抽取一个篮球是优等品的概率的估计值是________.(精确到0.01)
13.如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为________.
14.如图,在△ABC中,AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,则CD的长为________.
15.对于四边形ABCD,有四个条件:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从中任选两个作为已知条件,能判定四边形ABCD是平行四边形的概率是________.
16.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于________.
17.从-2,0,2这三个数中,任取两个不同的数分别作为a,b的值,恰好使得关于x的方程x2+ax-b=0有实数解的概率为________.
18.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2
cm的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为________cm2.(圆周率用π表示)
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,四边形ABCD是⊙O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.
(1)求证:AB=CD.
(2)若∠A=66°,求∠ADB的度数.
20.在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球试验,他们将30个与红球大小完全相同的白球装入试验袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次试验汇总后统计的数据:
摸球的次数s
150
200
500
900
1
000
1
200
摸到白球的频数n
51
64
156
275
303
361
摸到白球的频率
0.34
0.32
0.312
0.306
0.303
0.301
(1)请估计:当次数s很大时,摸到白球的频率将会接近________;假如你去摸一次,你摸到红球的概率是________(精确到0.1).
(2)试估算口袋中红球有多少个?
21.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠B=30°,AB=8,求DE的长.
22.有两个可以自由转动的均匀转盘,都被分成了3等份,并在每一份内标有数字,如图,规则如下:
①分别转动转盘A,B;②两个转盘停止后观察两个指针所指的数字(若指针指在等分线上,则重转一次,直到指针指向某一数字为止).
(1)用列表法分别求出“两个指针所指的数字都是方程x2-5x+6=0的解”的概率和“两个指针所指的数字都不是方程x2-5x+6=0的解”的概率;
(2)王磊和张浩想用这两个转盘做游戏,他们规定:“若两个指针所指的数字都是x2-5x+6=0的解”时,王磊得1分;若“两个指针所指的数字都不是x2-5x+6=0的解”时,张浩得3分,这个游戏公平吗?若你认为不公平,请修改得分规定,使游戏对双方公平.
23.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
24.图①和图②中,优弧AB所在⊙O的半径为2,AB=2
.点P为优弧AB上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是________,当BP经过点O时,∠ABA′=________;
(2)当BA′与⊙O相切时,如图②,求折痕BP的长;
(3)若线段BA′与优弧AB只有一个公共点B,设∠ABP=α,确定α的取值范围.
答案
一、1.C 2.C 3.D 4.B
5.A 点拨:如图,连接OC.
∵∠DOB=120°,
∴∠AOD=60°.
∵=,
∴∠DOC=∠BOC=60°,
∴∠AOD=∠DOC,
∴=,
∴OD⊥AC,
∴∠A=30°.
设OA=r,则OE=r=DE=1,
∴r=2,即OA=2,
∴AE==.
6.B 7.A 8.C
9.C 点拨:如图,点A运动的路径与x轴围成的面积为S1+S2+S3+S4+S5=+++2×=π+1.故选C.
10.B 点拨:如图,∵点A,B的坐标分别是(2,0),(6,0),
∴AB的中点M的坐标为(4,0),且点M是圆心,
作MN⊥CD于点N,则EN=FN,
又由抛物线的对称性可知CN=DN,
∴CE=DF.连接EM.
在Rt△EMN中,EN====1.
又CN=4-1=3,
∴CE=CN-EN=3-1=2,
∴CE+DF=2+2=4.
二、11. 12.0.94
13.75°
点拨:如图,连接DO,FO,
∵在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°.
∵内切圆O与边AB,BC,CA分别相切于点D,E,F,
∴∠ODA=∠OFA=90°,
∴∠DOF=150°,
∴∠DEF=∠DOF=75°.
14. 点拨:如图,过点A作AE⊥BD于点E,连接AD,
∴AD=AB=5,
根据垂径定理,得DE=BE,
∴CE=BE-BC=DE-2,
根据勾股定理,得AD2-DE2=AC2-CE2,
∴52-DE2=42-(DE-2)2,
解得DE=,
∴CD=DE+CE=2DE-2=.
15. 16.54° 17.
18.(2π-2
) 点拨:如图,过A作AD⊥BC于D.
由题意得AB=AC=BC=2
cm,∠BAC=∠ABC=∠ACB=60°,
∴AD=AB·sin
60°=2×=(cm),
∴△ABC的面积=BC·AD=
cm2,
S扇形BAC==π(cm2),
∴“莱洛三角形”的面积=3×π-2×=2π-2
(cm2).
三、19.(1)证明:∵DB平分∠ADC,
∴=.
∵OC⊥BD,
∴=,
∴=,
∴AB=CD.
(2)解:∵四边形ABCD是⊙O的内接四边形,
∴∠BCD=180°-∠A=114°.
∵=,
∴BC=CD,
∴∠BDC=×(180°-114°)=33°.
∵DB平分∠ADC,
∴∠ADB=∠BDC=33°.
20.解:(1)0.3;0.7
(2)设口袋中红球有x个,
由题意得0.7=,
解得x=70,
经检验x=70是原方程的解.
∴估计口袋中红球有70个.
21.(1)证明:如图,连接OD,
则OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C.
∴∠ODB=∠C.
∴OD∥AC.
∴∠ODE=∠DEC=90°.
∴DE是⊙O的切线.
(2)解:如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴BD=AB·cos
B=8×=4
.
又∵AB=AC,
∴CD=BD=4
,∠C=∠B=30°.
∴DE=CD=2
.
22.解:(1)解方程x2-5x+6=0,
得x1=2,x2=3,列表如下:
2
3
4
1
1,2
1,3
1,4
2
2,2
2,3
2,4
3
3,2
3,3
3,4
由表知,两个指针所指的数字都是该方程的解的概率是,两个指针所指的数字都不是该方程的解的概率是.
(2)因为1×≠3×,所以游戏不公平.
修改得分规定为:若两个指针所指的数字都是x2-5x+6=0的解时,王磊得1分;若两个指针所指的数字都不是x2-5x+6=0的解时,张浩得4分.(修改得分规定不唯一)
23.(1)证明:如图,连接OC.
∵AD⊥EF,
∴∠ADC=90°.
∴∠ACD+∠CAD=90°.
∵OC=OA,
∴∠ACO=∠CAO.
∵∠DAC=∠BAC,
∴∠ACD+∠ACO=90°,
即∠OCD=90°.
∴EF是⊙O的切线.
(2)证明:如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠ADC=90°=∠ACB.
∵∠DAC=∠BAC,
∴△ACD∽△ABC.
∴=,
即AC2=AD·AB.
(3)解:∵∠OCD=90°,
∠ACD=30°,
∴∠OCA=60°.
∵OC=OA,
∴△ACO是等边三角形.
∴AC=OC=2,∠AOC=60°.
在Rt△ADC中,
∵∠ACD=30°,
∴AD=1,CD=.
∴S阴影=S梯形OCDA-S扇形OCA=(1+2)×-=-.
24.解:(1)1;60°
(2)如图,作OC⊥AB于点C,
连接OB.
∵BA′与⊙O相切,
∴∠OBA′=90°.
在Rt△OBC中,
∵OB=2,OC=1,
∴sin
∠OBC==.
∴∠OBC=30°.
∴∠ABP=∠ABA′=
(∠OBA′+∠OBC)=60°.
∴∠OBP=30°.
作OD⊥BP于点D,则BP=2BD.
∵BD=OB·cos
30°=,
∴BP=2
.
(3)∵点P,A不重合,
∴α>0°.
由(1)得,当α增大到30°时,点A′在优弧AB上,
∴当0°<α<30°时,点A′在⊙O内,线段BA′与优弧AB只有一个公共点B.
由(2)知,α增大到60°时,BA′与⊙O相切,即线段BA′与优弧AB只有一个公共点B.
当α继续增大时,点P逐渐靠近点B,但点P,B不重合,
∴∠OBP<90°.
∵α=∠OBA+∠OBP,∠OBA=30°,
∴α<120°.
∴当60°≤α<120°时,线段BA′与优弧AB只有一个公共点B.
综上所述,α的取值范围是0°<α<30°或60°≤α<120°.
同课章节目录
