鲁教版五四制九年级下册 第六章对概率的进一步认识达标检测卷(word含答案)
文档属性
| 名称 | 鲁教版五四制九年级下册 第六章对概率的进一步认识达标检测卷(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 19:52:45 | ||
图片预览




文档简介
第六章达标检测卷
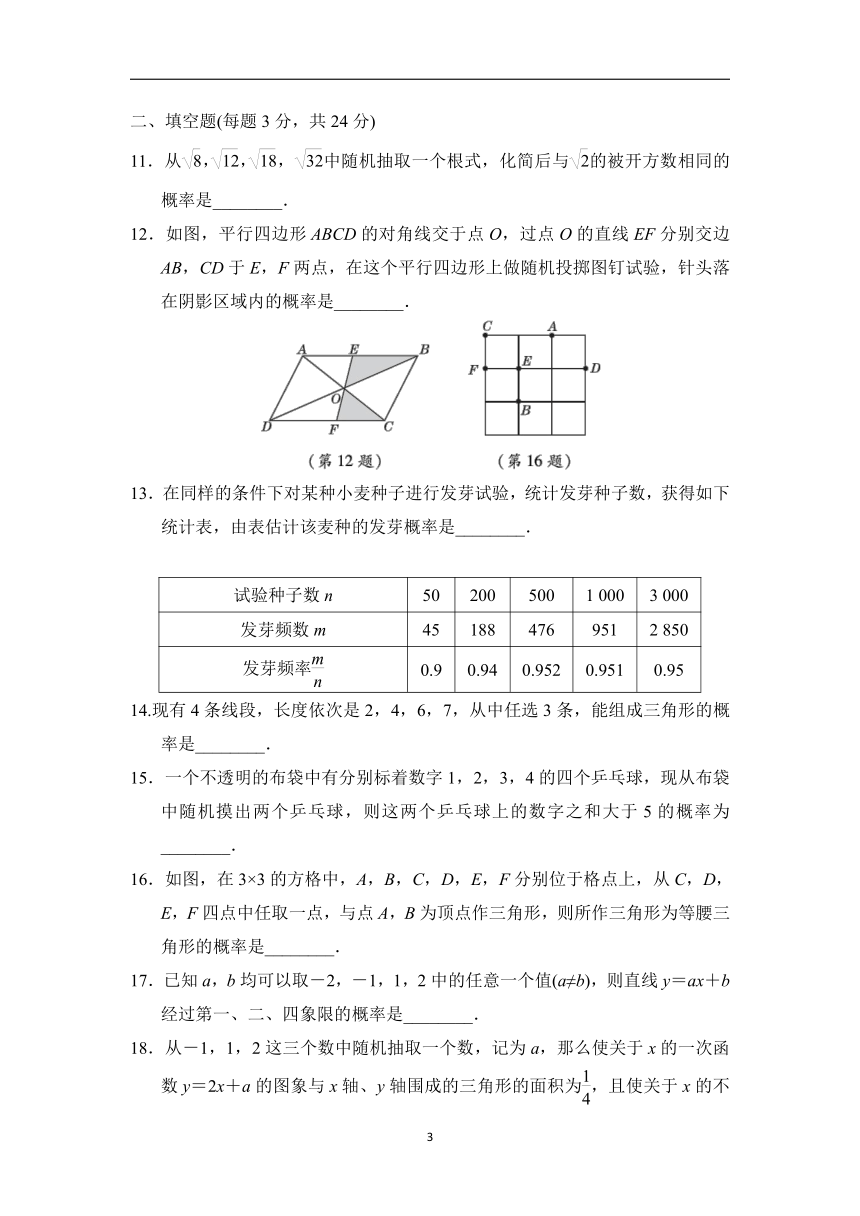
一、选择题(每题3分,共30分)
1.小明、小雪、丁丁和东东在公园玩飞行棋,四人轮流掷骰子,小明掷骰子7次就掷出了4次6,则小明掷到数字6的概率是( )
A.
B.
C.
D.不能确定
2.从一定高度抛一个瓶盖100次,落地后盖面朝下的有55次,则下列说法中错误的是( )
A.盖面朝下的频数是55
B.盖面朝下的频率是0.55
C.盖面朝下的概率不一定是0.55
D.同样的试验做200次,落地后盖面朝下的有110次
3.现有4张卡片,其中3张卡片正面上的图案是“”,1张卡片正面上的图案是“”,它们除此之外完全相同,把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面上图案相同的概率是( )
A.
B.
C.
D.
4.质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2
5.某展览大厅有2个入口和2个出口,其示意图如图所示,参观者可从任意一个入口进入,参观结束后可从任意一个出口离开.小明从入口1进入并从出口A离开的概率是( )
A.
B.
C.
D.
6.在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的概率是0.3,则估计盒子中大约有红球( )
A.16个
B.14个
C.20个
D.30个
7.若标有A,B,C的三只灯笼按图所示悬挂,每次摘取一只(摘B前需先摘C),直到摘完,则最后一只摘到B的概率是( )
A.
B.
C.
D.
8.用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A.
B.
C.
D.
9.一个盒子里有完全相同的三个小球,球上分别标有数-1,1,2.随机摸出一个小球(不放回),其数记为p,再随机摸出另一个小球,其数记为q,则满足关于x的方程x2-px+q=0有实数根的概率是( )
A.
B.
C.
D.
10.如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为( )
A.
B.
C.
D.
二、填空题(每题3分,共24分)
11.从,,,中随机抽取一个根式,化简后与的被开方数相同的概率是________.
12.如图,平行四边形ABCD的对角线交于点O,过点O的直线EF分别交边AB,CD于E,F两点,在这个平行四边形上做随机投掷图钉试验,针头落在阴影区域内的概率是________.
13.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下统计表,由表估计该麦种的发芽概率是________.
试验种子数n
50
200
500
1
000
3
000
发芽频数m
45
188
476
951
2
850
发芽频率
0.9
0.94
0.952
0.951
0.95
14.现有4条线段,长度依次是2,4,6,7,从中任选3条,能组成三角形的概率是________.
15.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从布袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为________.
16.如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是________.
17.已知a,b均可以取-2,-1,1,2中的任意一个值(a≠b),则直线y=ax+b经过第一、二、四象限的概率是________.
18.从-1,1,2这三个数中随机抽取一个数,记为a,那么使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为,且使关于x的不等式组有解的概率为________.
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.把一副普通扑克牌中的4张:黑桃2,红桃3,梅花4,方块5,洗匀后正面朝下放在桌面上.
(1)从中随机抽取一张牌是红心的概率是________;
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张.请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
20.一个不透明的口袋中有9个红球和若干个白球,这些球除颜色不同外,其余都相同.在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的数量:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色……小明重复上述过程,共摸了100次,其中40次摸到白球,请回答:口袋中的白球约有多少个?
21.某小区为了改善生态环境、促进生活垃圾的分类处理,将生活垃圾分为三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共1
000
t生活垃圾,数据统计如下(单位:t):
A
B
C
a
400
100
100
b
30
240
30
c
20
20
60
试估计“厨余垃圾”投放正确的概率.
22.为庆祝中国共产党成立100周年,在中小学生心中厚植爱党情怀,某市开展“童心向党”教育实践活动,某校准备组织学生参加唱歌,舞蹈,书法,国学诵读活动,为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一项)的问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)这次抽样调查的总人数为________人,扇形统计图中“舞蹈”对应的圆心角度数为________.
(2)若该校有1
400名学生,估计选择参加书法的有多少人?
(3)学校准备从推荐的4名同学(两男两女)中选取2人主持活动,利用画树状图法或列表法求恰为一男一女的概率.
23.有四张背面完全相同的卡片,正面分别写有数字2,0,2,0,如图,将卡片洗匀后,背面朝上放置在桌面上,甲、乙两人进行如下游戏:甲先抽一张卡片不放回,乙再抽一张卡片.
(1)已知甲抽到的卡片是数字2,则乙抽到卡片上的数字也是2的概率是________.
(2)甲、乙约定:若甲抽到卡片上的数字比乙大,则甲胜,否则乙胜,你认为这个游戏是否公平?用画树状图或列表的方法加以说明.
24.端午节吃粽子是中华民族的传统习俗,今年某商场销售甲厂家的高档、中档、低档三个品种及乙厂家的精装、简装两个品种的盒装粽子.现需要在甲、乙两个厂家中各选购一个品种.
(1)写出所有选购方案(利用树状图或表格求选购方案).
(2)如果(1)中各种选购方案被选中的可能性相同,那么甲厂家的高档粽子被选中的概率是多少?
(3)现某中学准备购买两个品种的粽子共32盒(价格如下表)发给学校的“留守儿童”,让他们过一个愉快的端午节,其中指定购买了甲厂家的高档粽子,再从乙厂家购买一个品种.若恰好用了1
200元,请问:购买了多少盒甲厂家的高档粽子?
品种
高档
中档
低档
精装
简装
价格/(元/盒)
60
40
25
50
20
答案
一、1.B 2.D 3.D 4.C 5.C 6.B
7.C 点拨:画树状图如图:由树状图可知,共有3种等可能的结果,最后一只摘到B的结果有2种,∴最后一只摘到B的概率为.
8.C 9.A
10.B 点拨:如图,正六边形的六个顶点中,连接任意两点可得15条线段,其中AC,AE,BD,BF,CE,DF这6条线段的长度为,∴所求概率为=.
二、11. 12. 13.0.95 14.
15. 16. 17. 18.
三、19.解:(1)
(2)用列表法表示所有可能出现的结果情况如下:
共有12种等可能的结果,其中和大于7的有4种,
所以抽取的两张牌牌面数字之和大于7的概率为=.
20.解:设口袋中的白球约有x个.
根据题意,得=,
解得x=6,
经检验,x=6是原方程的根.
答:口袋中的白球约有6个.
21.解:(1)三类垃圾随机投入三类垃圾箱的树状图如图所示.
由树状图可知,垃圾投放正确的概率为=.
(2)“厨余垃圾”投放正确的概率为
=.
22.解:(1)200;108°
(2)1
400×=560(人),
即估计选择参加书法的有560人.
(3)画树状图如图:
共有12种等可能的结果,其中恰为一男一女的结果有8种,
∴恰为一男一女的概率为=.
23.解:(1)
(2)这个游戏不公平.
理由如下:画树状图如图:
由图可知共有12种等可能的结果,甲抽到卡片上的数字比乙大的有4种情况,故甲获胜的概率为=,则乙获胜的概率为,故这个游戏不公平.
24.解:(1)画树状图如图所示:
或列表如下:
甲厂家乙厂家
高档
中档
低档
精装
(高档,精装)
(中档,精装)
(低档,精装)
简装
(高档,简装)
(中档,简装)
(低档,简装)
共有6种选购方案:(高档,精装),(高档,简装),(中档,精装),(中档,简装),(低档,精装),(低档,简装).
(2)因为选中甲厂家的高档粽子的方案有2种,即(高档,精装),(高档,简装),所以甲厂家的高档粽子被选中的概率为=.
(3)当选用方案(高档,精装)时,设分别购买高档粽子、精装粽子x1盒、y1盒,根据题意,
得
解得
经检验,不符合题意,舍去.
当选用方案(高档,简装)时,设分别购买高档粽子、简装粽子x2盒、y2盒,根据题意,得
解得
经检验,符合题意.故该中学购买了14盒甲厂家的高档粽子.
一、选择题(每题3分,共30分)
1.小明、小雪、丁丁和东东在公园玩飞行棋,四人轮流掷骰子,小明掷骰子7次就掷出了4次6,则小明掷到数字6的概率是( )
A.
B.
C.
D.不能确定
2.从一定高度抛一个瓶盖100次,落地后盖面朝下的有55次,则下列说法中错误的是( )
A.盖面朝下的频数是55
B.盖面朝下的频率是0.55
C.盖面朝下的概率不一定是0.55
D.同样的试验做200次,落地后盖面朝下的有110次
3.现有4张卡片,其中3张卡片正面上的图案是“”,1张卡片正面上的图案是“”,它们除此之外完全相同,把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面上图案相同的概率是( )
A.
B.
C.
D.
4.质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2
5.某展览大厅有2个入口和2个出口,其示意图如图所示,参观者可从任意一个入口进入,参观结束后可从任意一个出口离开.小明从入口1进入并从出口A离开的概率是( )
A.
B.
C.
D.
6.在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的概率是0.3,则估计盒子中大约有红球( )
A.16个
B.14个
C.20个
D.30个
7.若标有A,B,C的三只灯笼按图所示悬挂,每次摘取一只(摘B前需先摘C),直到摘完,则最后一只摘到B的概率是( )
A.
B.
C.
D.
8.用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A.
B.
C.
D.
9.一个盒子里有完全相同的三个小球,球上分别标有数-1,1,2.随机摸出一个小球(不放回),其数记为p,再随机摸出另一个小球,其数记为q,则满足关于x的方程x2-px+q=0有实数根的概率是( )
A.
B.
C.
D.
10.如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取到长度为的线段的概率为( )
A.
B.
C.
D.
二、填空题(每题3分,共24分)
11.从,,,中随机抽取一个根式,化简后与的被开方数相同的概率是________.
12.如图,平行四边形ABCD的对角线交于点O,过点O的直线EF分别交边AB,CD于E,F两点,在这个平行四边形上做随机投掷图钉试验,针头落在阴影区域内的概率是________.
13.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下统计表,由表估计该麦种的发芽概率是________.
试验种子数n
50
200
500
1
000
3
000
发芽频数m
45
188
476
951
2
850
发芽频率
0.9
0.94
0.952
0.951
0.95
14.现有4条线段,长度依次是2,4,6,7,从中任选3条,能组成三角形的概率是________.
15.一个不透明的布袋中有分别标着数字1,2,3,4的四个乒乓球,现从布袋中随机摸出两个乒乓球,则这两个乒乓球上的数字之和大于5的概率为________.
16.如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是________.
17.已知a,b均可以取-2,-1,1,2中的任意一个值(a≠b),则直线y=ax+b经过第一、二、四象限的概率是________.
18.从-1,1,2这三个数中随机抽取一个数,记为a,那么使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为,且使关于x的不等式组有解的概率为________.
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.把一副普通扑克牌中的4张:黑桃2,红桃3,梅花4,方块5,洗匀后正面朝下放在桌面上.
(1)从中随机抽取一张牌是红心的概率是________;
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张.请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
20.一个不透明的口袋中有9个红球和若干个白球,这些球除颜色不同外,其余都相同.在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的数量:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色……小明重复上述过程,共摸了100次,其中40次摸到白球,请回答:口袋中的白球约有多少个?
21.某小区为了改善生态环境、促进生活垃圾的分类处理,将生活垃圾分为三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共1
000
t生活垃圾,数据统计如下(单位:t):
A
B
C
a
400
100
100
b
30
240
30
c
20
20
60
试估计“厨余垃圾”投放正确的概率.
22.为庆祝中国共产党成立100周年,在中小学生心中厚植爱党情怀,某市开展“童心向党”教育实践活动,某校准备组织学生参加唱歌,舞蹈,书法,国学诵读活动,为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一项)的问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)这次抽样调查的总人数为________人,扇形统计图中“舞蹈”对应的圆心角度数为________.
(2)若该校有1
400名学生,估计选择参加书法的有多少人?
(3)学校准备从推荐的4名同学(两男两女)中选取2人主持活动,利用画树状图法或列表法求恰为一男一女的概率.
23.有四张背面完全相同的卡片,正面分别写有数字2,0,2,0,如图,将卡片洗匀后,背面朝上放置在桌面上,甲、乙两人进行如下游戏:甲先抽一张卡片不放回,乙再抽一张卡片.
(1)已知甲抽到的卡片是数字2,则乙抽到卡片上的数字也是2的概率是________.
(2)甲、乙约定:若甲抽到卡片上的数字比乙大,则甲胜,否则乙胜,你认为这个游戏是否公平?用画树状图或列表的方法加以说明.
24.端午节吃粽子是中华民族的传统习俗,今年某商场销售甲厂家的高档、中档、低档三个品种及乙厂家的精装、简装两个品种的盒装粽子.现需要在甲、乙两个厂家中各选购一个品种.
(1)写出所有选购方案(利用树状图或表格求选购方案).
(2)如果(1)中各种选购方案被选中的可能性相同,那么甲厂家的高档粽子被选中的概率是多少?
(3)现某中学准备购买两个品种的粽子共32盒(价格如下表)发给学校的“留守儿童”,让他们过一个愉快的端午节,其中指定购买了甲厂家的高档粽子,再从乙厂家购买一个品种.若恰好用了1
200元,请问:购买了多少盒甲厂家的高档粽子?
品种
高档
中档
低档
精装
简装
价格/(元/盒)
60
40
25
50
20
答案
一、1.B 2.D 3.D 4.C 5.C 6.B
7.C 点拨:画树状图如图:由树状图可知,共有3种等可能的结果,最后一只摘到B的结果有2种,∴最后一只摘到B的概率为.
8.C 9.A
10.B 点拨:如图,正六边形的六个顶点中,连接任意两点可得15条线段,其中AC,AE,BD,BF,CE,DF这6条线段的长度为,∴所求概率为=.
二、11. 12. 13.0.95 14.
15. 16. 17. 18.
三、19.解:(1)
(2)用列表法表示所有可能出现的结果情况如下:
共有12种等可能的结果,其中和大于7的有4种,
所以抽取的两张牌牌面数字之和大于7的概率为=.
20.解:设口袋中的白球约有x个.
根据题意,得=,
解得x=6,
经检验,x=6是原方程的根.
答:口袋中的白球约有6个.
21.解:(1)三类垃圾随机投入三类垃圾箱的树状图如图所示.
由树状图可知,垃圾投放正确的概率为=.
(2)“厨余垃圾”投放正确的概率为
=.
22.解:(1)200;108°
(2)1
400×=560(人),
即估计选择参加书法的有560人.
(3)画树状图如图:
共有12种等可能的结果,其中恰为一男一女的结果有8种,
∴恰为一男一女的概率为=.
23.解:(1)
(2)这个游戏不公平.
理由如下:画树状图如图:
由图可知共有12种等可能的结果,甲抽到卡片上的数字比乙大的有4种情况,故甲获胜的概率为=,则乙获胜的概率为,故这个游戏不公平.
24.解:(1)画树状图如图所示:
或列表如下:
甲厂家乙厂家
高档
中档
低档
精装
(高档,精装)
(中档,精装)
(低档,精装)
简装
(高档,简装)
(中档,简装)
(低档,简装)
共有6种选购方案:(高档,精装),(高档,简装),(中档,精装),(中档,简装),(低档,精装),(低档,简装).
(2)因为选中甲厂家的高档粽子的方案有2种,即(高档,精装),(高档,简装),所以甲厂家的高档粽子被选中的概率为=.
(3)当选用方案(高档,精装)时,设分别购买高档粽子、精装粽子x1盒、y1盒,根据题意,
得
解得
经检验,不符合题意,舍去.
当选用方案(高档,简装)时,设分别购买高档粽子、简装粽子x2盒、y2盒,根据题意,得
解得
经检验,符合题意.故该中学购买了14盒甲厂家的高档粽子.
