鲁教版五四制九年级下册 第五章圆 达标检测卷(word含答案)
文档属性
| 名称 | 鲁教版五四制九年级下册 第五章圆 达标检测卷(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1014.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览



文档简介
第五章达标检测卷
一、选择题(每题3分,共30分)
1.下列命题为真命题的是( )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.已如⊙O的半径等于3,圆心O到直线l的距离为5,那么直线l与⊙O的位置关系是( )
A.直线l与⊙O相交
B.直线l与⊙O相离
C.直线l与⊙O相切
D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.70°
B.60°
C.50°
D.30°
4.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
A.70°
B.64°
C.62°
D.51°
5.先画一个半径为4
cm的圆,再画出该圆的一个内接直角三角形,则这个内接直角三角形的斜边长是( )
A.2
cm
B.4
cm
C.4
cm
D.8
cm
6.如图,==,OB,OC分别交AC,BD于点E,F,则下列结论不一定正确的是( )
A.AC=BD
B.OE⊥AC,OF⊥BD
C.△OEF为等腰三角形
D.△OEF为等边三角形
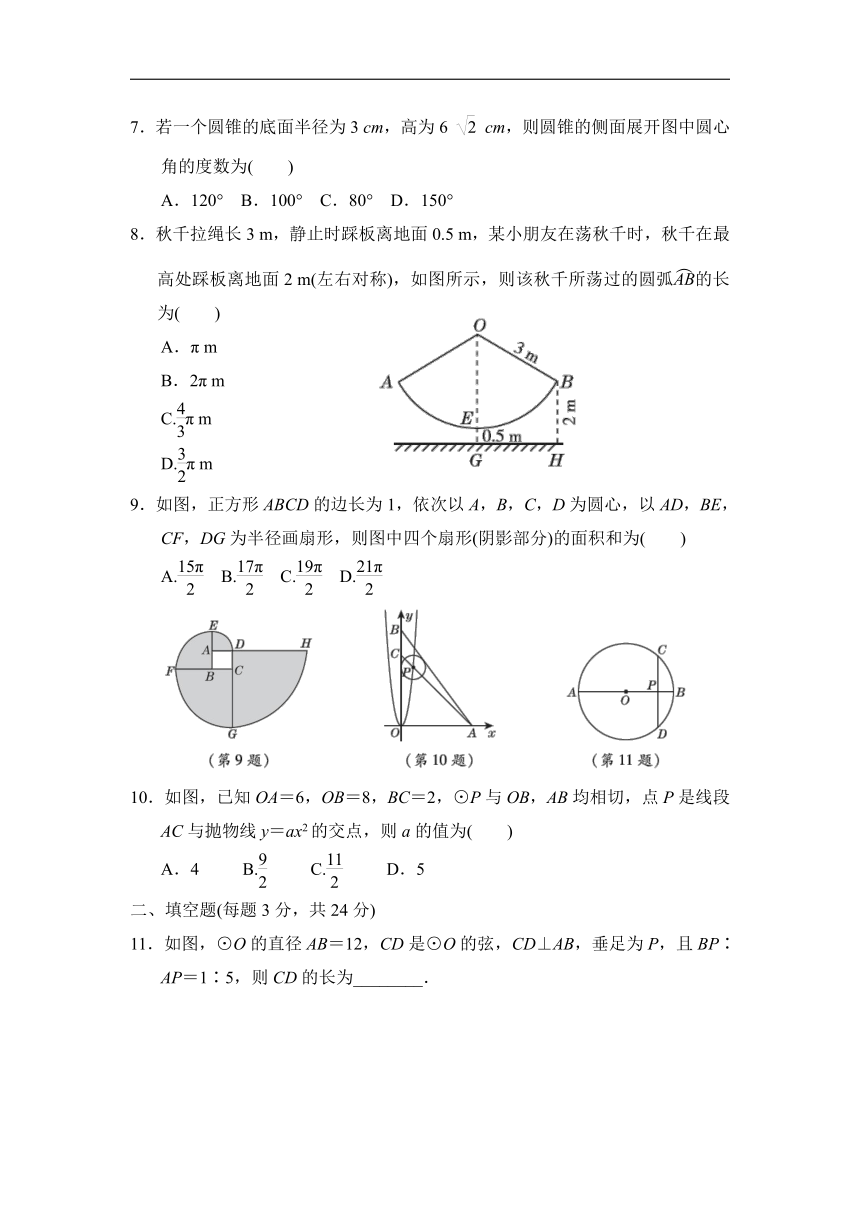
7.若一个圆锥的底面半径为3
cm,高为6
cm,则圆锥的侧面展开图中圆心角的度数为( )
A.120°
B.100°
C.80°
D.150°
8.秋千拉绳长3
m,静止时踩板离地面0.5
m,某小朋友在荡秋千时,秋千在最高处踩板离地面2
m(左右对称),如图所示,则该秋千所荡过的圆弧的长为( )
A.π
m
B.2π
m
C.π
m
D.π
m
9.如图,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,则图中四个扇形(阴影部分)的面积和为( )
A.
B.
C.
D.
10.如图,已知OA=6,OB=8,BC=2,⊙P与OB,AB均相切,点P是线段AC与抛物线y=ax2的交点,则a的值为( )
A.4
B.
C.
D.5
二、填空题(每题3分,共24分)
11.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5,则CD的长为________.
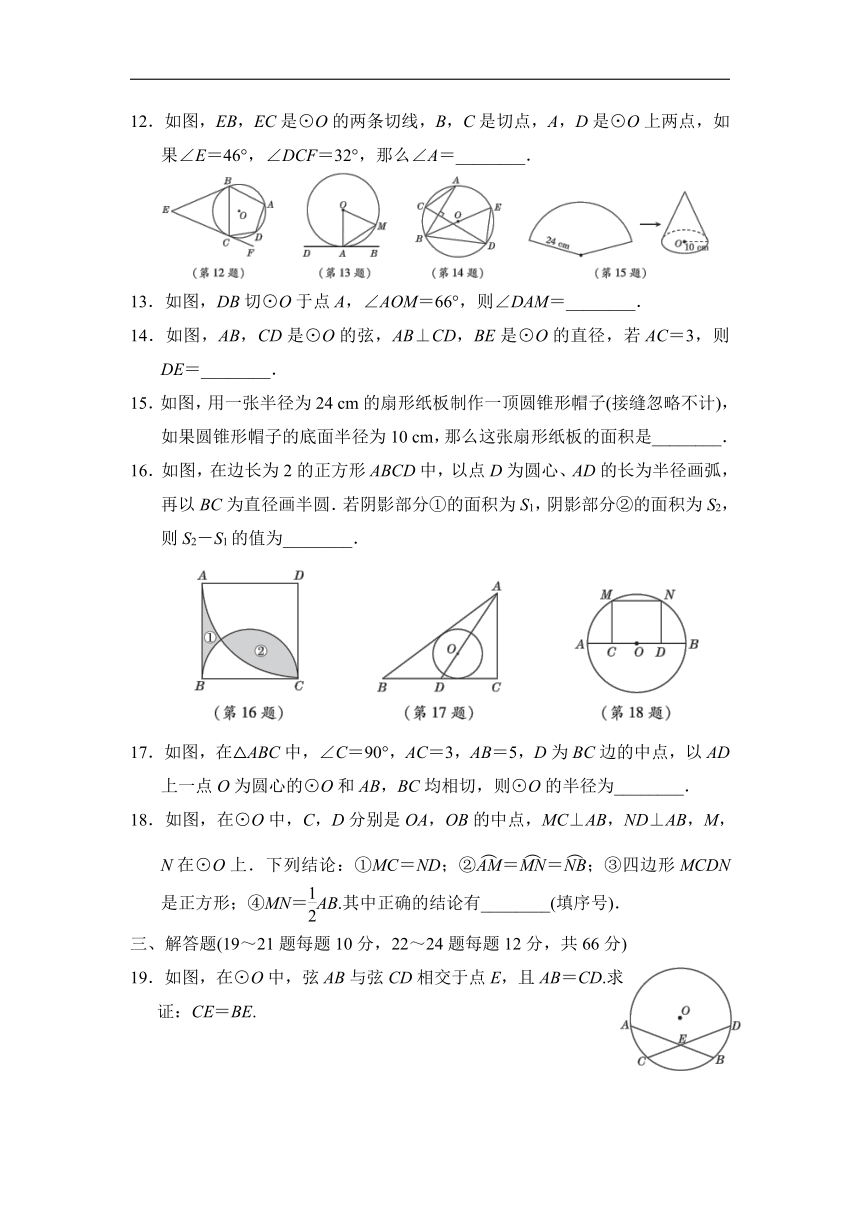
12.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A=________.
13.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=________.
14.如图,AB,CD是⊙O的弦,AB⊥CD,BE是⊙O的直径,若AC=3,则DE=________.
15.如图,用一张半径为24
cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10
cm,那么这张扇形纸板的面积是________.
16.如图,在边长为2的正方形ABCD中,以点D为圆心、AD的长为半径画弧,再以BC为直径画半圆.若阴影部分①的面积为S1,阴影部分②的面积为S2,则S2-S1的值为________.
17.如图,在△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB,BC均相切,则⊙O的半径为________.
18.如图,在⊙O中,C,D分别是OA,OB的中点,MC⊥AB,ND⊥AB,M,N在⊙O上.下列结论:①MC=ND;②==;③四边形MCDN是正方形;④MN=AB.其中正确的结论有________(填序号).
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
20.如图,AB是⊙O的直径,BD是⊙O的一条弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC.
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
21.如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为,AB=4.
(1)求点B,P,C的坐标.
(2)求证:CD是⊙P的切线.
22.如图,CB和CD切⊙O于B,D两点,A为圆周上一点,且∠1:∠2:∠3=1:2:3,BC=3,求扇形AOD的面积S.
23.如图是一拱形公路桥,圆弧形桥拱的水面跨度AB=80
m,桥拱到水面的最大高度为20
m.
(1)求桥拱所在圆的半径.
(2)现有一艘宽60
m,顶部截面为长方形且高出水面9
m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
24.如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线.
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长.
(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
答案
一、1.C 2.B 3.B 4.B 5.D 6.D
7.A 8.B
9.A 点拨:易知AD=1,BE=2,CF=3,DG=4,
所以四个扇形(阴影部分)的面积和=S扇形DAE+S扇形EBF+S扇形FCG+S扇形GDH=+++=
π.
10.D 点拨:如图,设⊙P与OB,AB分别相切于点M,N,连接PM,PN.
设⊙P的半径为t,则PN=PM=t.
由题意知OC=AO=6,则∠OCA=45°,
∴CM=MP=t,
易知A(6,0),C(0,6).
由点A,C的坐标,得直线AC的表达式为y=-x+6,
则点P的坐标为(t,-t+6),
由点P,A的坐标,得PA=(6-t),则AN==,
∵⊙P与OB,AB分别相切于点M,N,
∴BN=BM=BC+CM=2+t.
在Rt△ABO中,OA=6,OB=8,则AB=10=AN+BN,
∴10=+2+t,
解得t=1.
故点P的坐标为(1,5),将点P的坐标代入y=ax2,得a=5.
二、11.4
12.99° 点拨:易知EB=EC.
又因为∠E=46°,
所以∠ECB=67°.
所以∠BCD=180°-67°-32°=81°.
在⊙O中,∠BCD与∠A互补,
所以∠A=180°-81°=99°.
13.147° 点拨:因为DB是⊙O的切线,所以OA⊥DB.所以∠OAD=90°.
由∠AOM=66°,OA=OM,
得∠OAM=×(180°-66°)=57°.
所以∠DAM=90°+57°=147°.
14.3 点拨:∵BE是⊙O的直径,
∴∠BDE=90°.
∴∠BDC+∠CDE=90°.
∵AB⊥CD,
∴∠ACD+∠CAB=90°.
∵∠CAB=∠BDC,
∴∠ACD=∠CDE.
∴=.∴-=-.
∴=.∴DE=AC=3.
15.240π
cm2 16.-4 17.
18.①②④ 点拨:如图,连接OM,ON,易证Rt△OMC≌Rt△OND,可得MC=ND,故①正确.在Rt△MOC中,CO=MO,可得∠CMO=30°,所以∠MOC=60°.易得∠MOC=∠NOD=∠MON=60°,所以==,故②正确.易得CD=AB=OA=OM,∵MC<OM,
∴MC<CD.∴四边形MCDN不是正方形,故③错误.易得MN=CD=AB,故④正确.
三、19.证明:连接BC,
∵AB=CD,∴=,
∴-=-,即=,
∴∠B=∠C,∴CE=BE.
20.(1)证明:如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,∴AB=AC.
(2)解:由(1)知AB=AC,
∵∠BAC=60°,∠ADB=90°,
∴△ABC是等边三角形,∠BAD=30°.
在Rt△BAD中,∠BAD=30°,
AB=8,∴BD=4,即DC=4.
又∵DE⊥AC,
∴DE=DC·sin
C=4·sin
60°=4×=2
.
21.(1)解:如图,连接CA.
∵OP⊥AB,
∴OB=OA=2.
∵OP2+OB2=BP2,
∴OP2=5-4=1,即OP=1.
∵BC是⊙P的直径,
∴∠CAB=90°.
∵CP=BP,OB=OA,
∴AC=2OP=2.
∴B(2,0),P(0,1),C(-2,2).
(2)证明:∵直线y=2x+b过点C(-2,2),
∴b=6.∴y=2x+6.
∵当y=0时,x=-3,
∴D(-3,0).∴AD=1.
∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,
∴△DAC≌△POB.
∴∠DCA=∠ABC.
又∵∠ACB+∠ABC=90°,
∴∠ACB+∠DCA=90°,即CD⊥BC.
∴CD是⊙P的切线.
22.解:∵CD为⊙O的切线,
∴∠ODC=90°,即OD⊥CD.
∵∠1?∠2?∠3=1?2?3,
∴∠1=15°,∠2=30°,∠3=45°.
如图,连接OB.
∵CB为⊙O的切线,
∴OB⊥BC,BC=CD.
∴∠CBD=∠3=45°,
∴∠OBD=45°.
又∵∠1+∠2=45°,
∴∠BOD=90°,即OD⊥OB.
∴OD∥BC,CD∥OB.
又∵OB=OD,
∴四边形OBCD为正方形.
∵BC=3,∴OB=3.
∵∠1=15°,∴∠AOB=30°,
∴∠AOD=120°.
∴S=×π×32=3π.
23.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,
延长EF交于点C,连接AE,
则CF=20
m.
由垂径定理知AF=FB=AB=40
m.
设半径是r
m,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2.
解得r=50.
∴桥拱所在圆的半径为50
m.
(2)这艘轮船能顺利通过.理由:
如图,假设MN=60
m,且MN∥AB,
连接EM,设EC与MN的交点为D,
∵EC⊥AB,∴DE⊥MN,
∴DM=30
m,
∴DE===40(m).
∵EF=EC-CF=50-20=30(m),
∴DF=DE-EF=40-30=10(m).
∵10
m>9
m,
∴这艘轮船能顺利通过.
24.(1)证明:如图,连接CD.
∵AD是⊙O的直径,
∴∠ACD=90°.
∴∠CAD+∠ADC=90°.
又∵∠PAC=∠PBA,
∠ADC=∠PBA,
∴∠PAC=∠ADC.
∴∠CAD+∠PAC=∠PAD=90°.
∴PA⊥DA.
又∵AD是⊙O的直径,
∴PA是⊙O的切线.
(2)解:由(1)知,PA⊥AD,
又∵CF⊥AD,∴CF∥PA.
∴∠GCA=∠PAC.
又∵∠PAC=∠PBA,
∴∠GCA=∠PBA.
又∵∠CAG=∠BAC,
∴△CAG∽△BAC.
∴=,
即AC2=AG·AB.
∵AG·AB=12,∴AC2=12.
∴AC=2
.
(3)解:设AF=x,
∵AF∶FD=1∶2,∴FD=2x.
∴AD=AF+FD=3x.
易知△ACF∽△ADC,
∴=,
即AC2=AF·AD.
∴3x2=12,
解得x=2或x=-2(舍去).
∴AF=2,AD=6.
∴⊙O的半径为3.
在Rt△AFG中,AF=2,GF=1,
根据勾股定理得AG===,
由(2)知AG·AB=12,
∴AB==.
如图,连接BD.
∵AD是⊙O的直径,
∴∠ABD=90°.
在Rt△ABD中,
∵sin∠ADB=,
AD=6,AB=,
∴sin∠ADB=.
又∵∠ACE=∠ADB,
∴sin∠ACE=.
一、选择题(每题3分,共30分)
1.下列命题为真命题的是( )
A.两点确定一个圆
B.度数相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2.已如⊙O的半径等于3,圆心O到直线l的距离为5,那么直线l与⊙O的位置关系是( )
A.直线l与⊙O相交
B.直线l与⊙O相离
C.直线l与⊙O相切
D.无法确定
3.如图,⊙O是△ABC的外接圆,∠BOC=120°,则∠BAC的度数是( )
A.70°
B.60°
C.50°
D.30°
4.如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
A.70°
B.64°
C.62°
D.51°
5.先画一个半径为4
cm的圆,再画出该圆的一个内接直角三角形,则这个内接直角三角形的斜边长是( )
A.2
cm
B.4
cm
C.4
cm
D.8
cm
6.如图,==,OB,OC分别交AC,BD于点E,F,则下列结论不一定正确的是( )
A.AC=BD
B.OE⊥AC,OF⊥BD
C.△OEF为等腰三角形
D.△OEF为等边三角形
7.若一个圆锥的底面半径为3
cm,高为6
cm,则圆锥的侧面展开图中圆心角的度数为( )
A.120°
B.100°
C.80°
D.150°
8.秋千拉绳长3
m,静止时踩板离地面0.5
m,某小朋友在荡秋千时,秋千在最高处踩板离地面2
m(左右对称),如图所示,则该秋千所荡过的圆弧的长为( )
A.π
m
B.2π
m
C.π
m
D.π
m
9.如图,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,则图中四个扇形(阴影部分)的面积和为( )
A.
B.
C.
D.
10.如图,已知OA=6,OB=8,BC=2,⊙P与OB,AB均相切,点P是线段AC与抛物线y=ax2的交点,则a的值为( )
A.4
B.
C.
D.5
二、填空题(每题3分,共24分)
11.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5,则CD的长为________.
12.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A=________.
13.如图,DB切⊙O于点A,∠AOM=66°,则∠DAM=________.
14.如图,AB,CD是⊙O的弦,AB⊥CD,BE是⊙O的直径,若AC=3,则DE=________.
15.如图,用一张半径为24
cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10
cm,那么这张扇形纸板的面积是________.
16.如图,在边长为2的正方形ABCD中,以点D为圆心、AD的长为半径画弧,再以BC为直径画半圆.若阴影部分①的面积为S1,阴影部分②的面积为S2,则S2-S1的值为________.
17.如图,在△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB,BC均相切,则⊙O的半径为________.
18.如图,在⊙O中,C,D分别是OA,OB的中点,MC⊥AB,ND⊥AB,M,N在⊙O上.下列结论:①MC=ND;②==;③四边形MCDN是正方形;④MN=AB.其中正确的结论有________(填序号).
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
20.如图,AB是⊙O的直径,BD是⊙O的一条弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC.
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
21.如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为,AB=4.
(1)求点B,P,C的坐标.
(2)求证:CD是⊙P的切线.
22.如图,CB和CD切⊙O于B,D两点,A为圆周上一点,且∠1:∠2:∠3=1:2:3,BC=3,求扇形AOD的面积S.
23.如图是一拱形公路桥,圆弧形桥拱的水面跨度AB=80
m,桥拱到水面的最大高度为20
m.
(1)求桥拱所在圆的半径.
(2)现有一艘宽60
m,顶部截面为长方形且高出水面9
m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
24.如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线.
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长.
(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
答案
一、1.C 2.B 3.B 4.B 5.D 6.D
7.A 8.B
9.A 点拨:易知AD=1,BE=2,CF=3,DG=4,
所以四个扇形(阴影部分)的面积和=S扇形DAE+S扇形EBF+S扇形FCG+S扇形GDH=+++=
π.
10.D 点拨:如图,设⊙P与OB,AB分别相切于点M,N,连接PM,PN.
设⊙P的半径为t,则PN=PM=t.
由题意知OC=AO=6,则∠OCA=45°,
∴CM=MP=t,
易知A(6,0),C(0,6).
由点A,C的坐标,得直线AC的表达式为y=-x+6,
则点P的坐标为(t,-t+6),
由点P,A的坐标,得PA=(6-t),则AN==,
∵⊙P与OB,AB分别相切于点M,N,
∴BN=BM=BC+CM=2+t.
在Rt△ABO中,OA=6,OB=8,则AB=10=AN+BN,
∴10=+2+t,
解得t=1.
故点P的坐标为(1,5),将点P的坐标代入y=ax2,得a=5.
二、11.4
12.99° 点拨:易知EB=EC.
又因为∠E=46°,
所以∠ECB=67°.
所以∠BCD=180°-67°-32°=81°.
在⊙O中,∠BCD与∠A互补,
所以∠A=180°-81°=99°.
13.147° 点拨:因为DB是⊙O的切线,所以OA⊥DB.所以∠OAD=90°.
由∠AOM=66°,OA=OM,
得∠OAM=×(180°-66°)=57°.
所以∠DAM=90°+57°=147°.
14.3 点拨:∵BE是⊙O的直径,
∴∠BDE=90°.
∴∠BDC+∠CDE=90°.
∵AB⊥CD,
∴∠ACD+∠CAB=90°.
∵∠CAB=∠BDC,
∴∠ACD=∠CDE.
∴=.∴-=-.
∴=.∴DE=AC=3.
15.240π
cm2 16.-4 17.
18.①②④ 点拨:如图,连接OM,ON,易证Rt△OMC≌Rt△OND,可得MC=ND,故①正确.在Rt△MOC中,CO=MO,可得∠CMO=30°,所以∠MOC=60°.易得∠MOC=∠NOD=∠MON=60°,所以==,故②正确.易得CD=AB=OA=OM,∵MC<OM,
∴MC<CD.∴四边形MCDN不是正方形,故③错误.易得MN=CD=AB,故④正确.
三、19.证明:连接BC,
∵AB=CD,∴=,
∴-=-,即=,
∴∠B=∠C,∴CE=BE.
20.(1)证明:如图,连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,∴AB=AC.
(2)解:由(1)知AB=AC,
∵∠BAC=60°,∠ADB=90°,
∴△ABC是等边三角形,∠BAD=30°.
在Rt△BAD中,∠BAD=30°,
AB=8,∴BD=4,即DC=4.
又∵DE⊥AC,
∴DE=DC·sin
C=4·sin
60°=4×=2
.
21.(1)解:如图,连接CA.
∵OP⊥AB,
∴OB=OA=2.
∵OP2+OB2=BP2,
∴OP2=5-4=1,即OP=1.
∵BC是⊙P的直径,
∴∠CAB=90°.
∵CP=BP,OB=OA,
∴AC=2OP=2.
∴B(2,0),P(0,1),C(-2,2).
(2)证明:∵直线y=2x+b过点C(-2,2),
∴b=6.∴y=2x+6.
∵当y=0时,x=-3,
∴D(-3,0).∴AD=1.
∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,
∴△DAC≌△POB.
∴∠DCA=∠ABC.
又∵∠ACB+∠ABC=90°,
∴∠ACB+∠DCA=90°,即CD⊥BC.
∴CD是⊙P的切线.
22.解:∵CD为⊙O的切线,
∴∠ODC=90°,即OD⊥CD.
∵∠1?∠2?∠3=1?2?3,
∴∠1=15°,∠2=30°,∠3=45°.
如图,连接OB.
∵CB为⊙O的切线,
∴OB⊥BC,BC=CD.
∴∠CBD=∠3=45°,
∴∠OBD=45°.
又∵∠1+∠2=45°,
∴∠BOD=90°,即OD⊥OB.
∴OD∥BC,CD∥OB.
又∵OB=OD,
∴四边形OBCD为正方形.
∵BC=3,∴OB=3.
∵∠1=15°,∴∠AOB=30°,
∴∠AOD=120°.
∴S=×π×32=3π.
23.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,
延长EF交于点C,连接AE,
则CF=20
m.
由垂径定理知AF=FB=AB=40
m.
设半径是r
m,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2.
解得r=50.
∴桥拱所在圆的半径为50
m.
(2)这艘轮船能顺利通过.理由:
如图,假设MN=60
m,且MN∥AB,
连接EM,设EC与MN的交点为D,
∵EC⊥AB,∴DE⊥MN,
∴DM=30
m,
∴DE===40(m).
∵EF=EC-CF=50-20=30(m),
∴DF=DE-EF=40-30=10(m).
∵10
m>9
m,
∴这艘轮船能顺利通过.
24.(1)证明:如图,连接CD.
∵AD是⊙O的直径,
∴∠ACD=90°.
∴∠CAD+∠ADC=90°.
又∵∠PAC=∠PBA,
∠ADC=∠PBA,
∴∠PAC=∠ADC.
∴∠CAD+∠PAC=∠PAD=90°.
∴PA⊥DA.
又∵AD是⊙O的直径,
∴PA是⊙O的切线.
(2)解:由(1)知,PA⊥AD,
又∵CF⊥AD,∴CF∥PA.
∴∠GCA=∠PAC.
又∵∠PAC=∠PBA,
∴∠GCA=∠PBA.
又∵∠CAG=∠BAC,
∴△CAG∽△BAC.
∴=,
即AC2=AG·AB.
∵AG·AB=12,∴AC2=12.
∴AC=2
.
(3)解:设AF=x,
∵AF∶FD=1∶2,∴FD=2x.
∴AD=AF+FD=3x.
易知△ACF∽△ADC,
∴=,
即AC2=AF·AD.
∴3x2=12,
解得x=2或x=-2(舍去).
∴AF=2,AD=6.
∴⊙O的半径为3.
在Rt△AFG中,AF=2,GF=1,
根据勾股定理得AG===,
由(2)知AG·AB=12,
∴AB==.
如图,连接BD.
∵AD是⊙O的直径,
∴∠ABD=90°.
在Rt△ABD中,
∵sin∠ADB=,
AD=6,AB=,
∴sin∠ADB=.
又∵∠ACE=∠ADB,
∴sin∠ACE=.
