冀教版九年级上册第27章 反比例函数27.3反比例函数的应用 课件(19张PPT)
文档属性
| 名称 | 冀教版九年级上册第27章 反比例函数27.3反比例函数的应用 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1008.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
九年级数学
27.3反比例函数的应用
学习目标
1、学会把实际问题转化为数学问题,进一步理解反比例函数关系式的构造,掌握用反比例函数的方法解决实际问题.
2、经历“实际问题——建立模型——拓展应用”的过程,发展分析问题,解决问题的能力。
教学重点:用反比例函数解决实际问题
教学难点:
构建反比例函数的数学模型
三、典型例题:
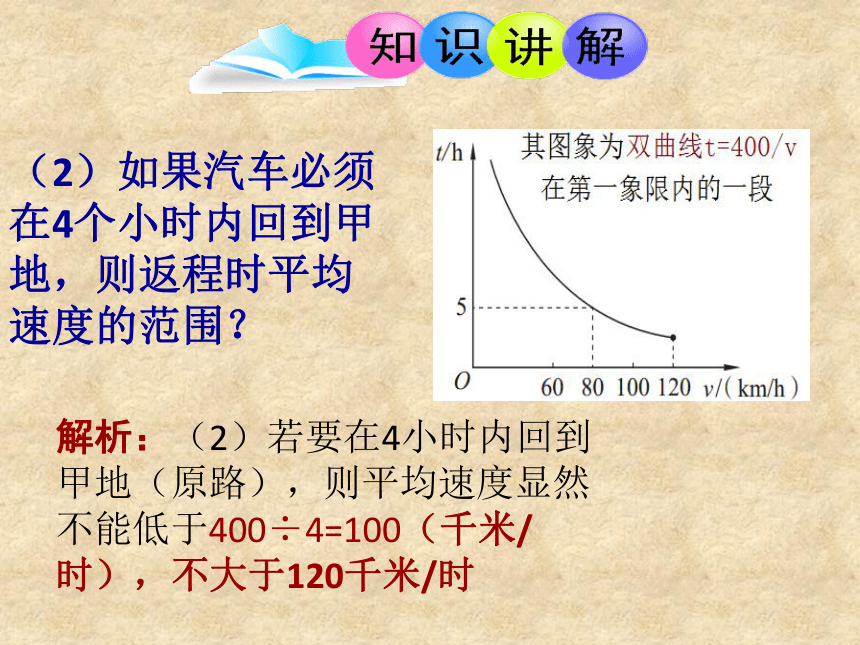
例5:一位汽车以80km/h的平均速度从甲地去乙地,用5小时到达.
(1)当汽车按原路返回时,如果该车限速120km/h,写出返回甲地所用的时间t与平均速度v的函数关系,并画出它的图象;
解析:(1)原路返回,说明路程不变,
则80×5=400千米,
由vt=400,及限速条件可得:
t=400/v,(0(2)如果汽车必须在4个小时内回到甲地,则返程时平均速度的范围?
解析:(2)若要在4小时内回到甲地(原路),则平均速度显然不能低于400÷4=100(千米/时),不大于120千米/时
解:
1.一定质量的二氧化碳,当它的体积
V=4m3
时,它的密度ρ=2.25kg/m3
.
(1)求V与ρ的函数关系式;
(2)求当V=6
m3时,二氧化碳的密度;
(3)结合函数图象回答:当V小于等于6
m3时,二氧化碳的密度有最大值还是最小值?最大(小)值是多少?
用函数解决实际问题的方法与步骤
1.审清题意,找出题目中的常量、变量,并理清常量与变量之间的关系;
2.根据常量与变量之间的关系,设出函数表达式,其中待定的系数用字母表示;
3.由题目中的已知条件列方程(组),求出待定系数;
4.写出函数表达式,要注意表达式中自变量的取值范围;
5.用函数的性质,以及综合利用方程、方程组、不等式等相关知识去解决实际问题
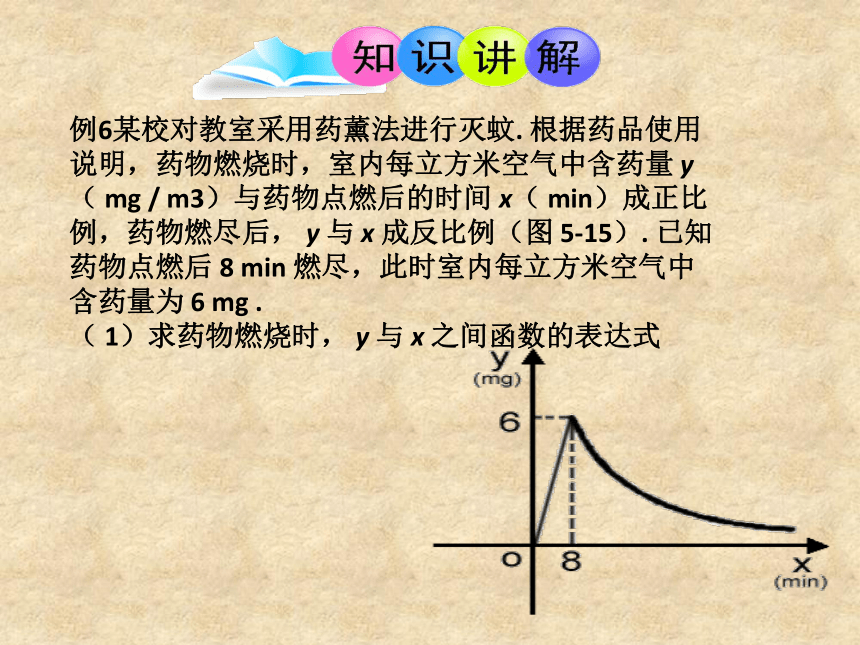
例6某校对教室采用药薰法进行灭蚊.
根据药品使用说明,药物燃烧时,室内每立方米空气中含药量
y(
mg
/
m3)与药物点燃后的时间
x(
min)成正比例,药物燃尽后,
y
与
x
成反比例(图
5-15).
已知药物点燃后
8
min
燃尽,此时室内每立方米空气中含药量为
6
mg
.
(
1)求药物燃烧时,
y
与
x
之间函数的表达式
(
2)求药物燃尽后,
y
与
x
之间函数的表达式;
解析:(1)当药物燃烧时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
(2)当药物燃烧尽时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
(
3)根据灭蚊药品使用说明,当空气中每立方米的含药量低于
1
.6
mg
时,对人体是安全的.
那么从开始药薰,至少经过多少时间,学生才能进入教室?
(
0≤x≤8)
(x>8)
解:(3)当y=1.6时有
答:至少经过30min后,学生才能回到教室;
1.6
30
(4)根据灭蚊药品使用说明,当每立方米空气中含药量不低于
3
mg
且持续时间不低于
10
min
时,才能有效杀灭室内的蚊虫,那么此次灭蚊是否有效?为什么?
(4)把y=3代入两函数得
∴持续时间=16-4=12(min)>10(min)
答:此次消毒有效。
3
4
16
解:(1)由图象可知,
当
时,y与x成正比例关系,
设
,k≠0
.
由图象可知,当
x=4时,y=8,
∴4k=8,解得:k=2;∴
又由题意可知:当
时,y与x成反比,设
,
m≠0
由图象可知,当x=4时,y=8,∴
;
∴
即:血液中药物浓度上升时
;
血液中药物浓度下降时
.
总结:
实际问题
数学模型(反比例函数)
转化
解决
1.本节课学习的数学知识:
运用反比例函数的知识解决实际问题。
2.本节课学习的数学方法:
建模思想、函数的思想、
数形结合思想
。
课堂达标
1.已知矩形的面积为10,长和宽分别为x和y,
则y关于x的函数图象大致是( )
A.
B.
C.
D.
C
2.如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
A
B
C
D
A
3.已知某种品牌电脑显示屏的使用寿命大约为
2×
104
h
.
如果该显示屏工作天数为
d(天),平均每天工作时间为
t(
h),那么能正确表示
d与
t
之间函数关系的图象是(
).
C
4.某勘探队在进行野外考察时,途中遇到一段湿地.
为了安全,他们沿着前进的路线铺设了若干块木板,构筑成一条临时通道.
已知木板对地面的压强
P(
Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
(
1)写出这个反比例函数的表达式和自变量的取值范围;
(
2)当木板面积为
0.2
m2时,木板对地面的压强是多少?
(
3)如果要求压强不超过
6
000
Pa,木板的面积至少要多大?
解;(1)
(2)
(3)
所以木板面积至少要0.1m2.
九年级数学
27.3反比例函数的应用
学习目标
1、学会把实际问题转化为数学问题,进一步理解反比例函数关系式的构造,掌握用反比例函数的方法解决实际问题.
2、经历“实际问题——建立模型——拓展应用”的过程,发展分析问题,解决问题的能力。
教学重点:用反比例函数解决实际问题
教学难点:
构建反比例函数的数学模型
三、典型例题:
例5:一位汽车以80km/h的平均速度从甲地去乙地,用5小时到达.
(1)当汽车按原路返回时,如果该车限速120km/h,写出返回甲地所用的时间t与平均速度v的函数关系,并画出它的图象;
解析:(1)原路返回,说明路程不变,
则80×5=400千米,
由vt=400,及限速条件可得:
t=400/v,(0
解析:(2)若要在4小时内回到甲地(原路),则平均速度显然不能低于400÷4=100(千米/时),不大于120千米/时
解:
1.一定质量的二氧化碳,当它的体积
V=4m3
时,它的密度ρ=2.25kg/m3
.
(1)求V与ρ的函数关系式;
(2)求当V=6
m3时,二氧化碳的密度;
(3)结合函数图象回答:当V小于等于6
m3时,二氧化碳的密度有最大值还是最小值?最大(小)值是多少?
用函数解决实际问题的方法与步骤
1.审清题意,找出题目中的常量、变量,并理清常量与变量之间的关系;
2.根据常量与变量之间的关系,设出函数表达式,其中待定的系数用字母表示;
3.由题目中的已知条件列方程(组),求出待定系数;
4.写出函数表达式,要注意表达式中自变量的取值范围;
5.用函数的性质,以及综合利用方程、方程组、不等式等相关知识去解决实际问题
例6某校对教室采用药薰法进行灭蚊.
根据药品使用说明,药物燃烧时,室内每立方米空气中含药量
y(
mg
/
m3)与药物点燃后的时间
x(
min)成正比例,药物燃尽后,
y
与
x
成反比例(图
5-15).
已知药物点燃后
8
min
燃尽,此时室内每立方米空气中含药量为
6
mg
.
(
1)求药物燃烧时,
y
与
x
之间函数的表达式
(
2)求药物燃尽后,
y
与
x
之间函数的表达式;
解析:(1)当药物燃烧时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
(2)当药物燃烧尽时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
(
3)根据灭蚊药品使用说明,当空气中每立方米的含药量低于
1
.6
mg
时,对人体是安全的.
那么从开始药薰,至少经过多少时间,学生才能进入教室?
(
0≤x≤8)
(x>8)
解:(3)当y=1.6时有
答:至少经过30min后,学生才能回到教室;
1.6
30
(4)根据灭蚊药品使用说明,当每立方米空气中含药量不低于
3
mg
且持续时间不低于
10
min
时,才能有效杀灭室内的蚊虫,那么此次灭蚊是否有效?为什么?
(4)把y=3代入两函数得
∴持续时间=16-4=12(min)>10(min)
答:此次消毒有效。
3
4
16
解:(1)由图象可知,
当
时,y与x成正比例关系,
设
,k≠0
.
由图象可知,当
x=4时,y=8,
∴4k=8,解得:k=2;∴
又由题意可知:当
时,y与x成反比,设
,
m≠0
由图象可知,当x=4时,y=8,∴
;
∴
即:血液中药物浓度上升时
;
血液中药物浓度下降时
.
总结:
实际问题
数学模型(反比例函数)
转化
解决
1.本节课学习的数学知识:
运用反比例函数的知识解决实际问题。
2.本节课学习的数学方法:
建模思想、函数的思想、
数形结合思想
。
课堂达标
1.已知矩形的面积为10,长和宽分别为x和y,
则y关于x的函数图象大致是( )
A.
B.
C.
D.
C
2.如图,市煤气公司计划在地下修建一个容积为104m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
A
B
C
D
A
3.已知某种品牌电脑显示屏的使用寿命大约为
2×
104
h
.
如果该显示屏工作天数为
d(天),平均每天工作时间为
t(
h),那么能正确表示
d与
t
之间函数关系的图象是(
).
C
4.某勘探队在进行野外考察时,途中遇到一段湿地.
为了安全,他们沿着前进的路线铺设了若干块木板,构筑成一条临时通道.
已知木板对地面的压强
P(
Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
(
1)写出这个反比例函数的表达式和自变量的取值范围;
(
2)当木板面积为
0.2
m2时,木板对地面的压强是多少?
(
3)如果要求压强不超过
6
000
Pa,木板的面积至少要多大?
解;(1)
(2)
(3)
所以木板面积至少要0.1m2.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
