1.5《函数 的图象(课时1)》(新人教版必修4)
文档属性
| 名称 | 1.5《函数 的图象(课时1)》(新人教版必修4) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-30 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
普通高中课程标准实验教科书必修④
函数y=Asin(ωx+φ)的图象
邯郸四中 杜瑞敏
1.“五点法”作y=sinx图象的“五点”指:
2.“五点法”作图的步骤:
列表,描点,成图
如何由函数y=sinx的图象变换得到函数y=Asin(ωx+φ)的图象
培养观察问题和探索问题的能力
(一)探索A,ω,φ对函数y=Asin(ωx+φ)(A>0, ω>0)图像的影响:
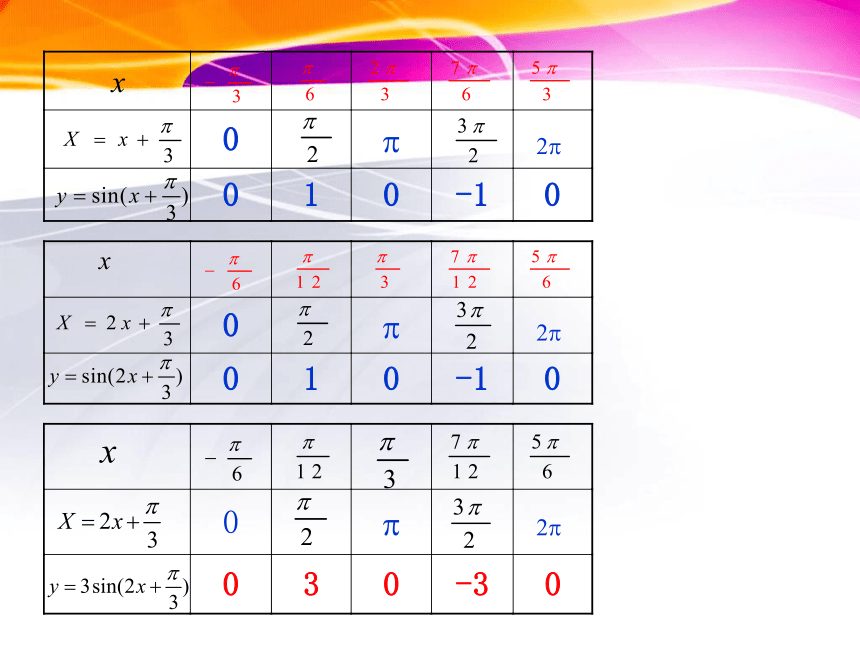
用“五点法”在同一坐标系画出下列几组函数(在一个周期的)图象,并说明它们之间的关系:
探究二: y=sin(x+π/3)与y=sin(2x+π/3)
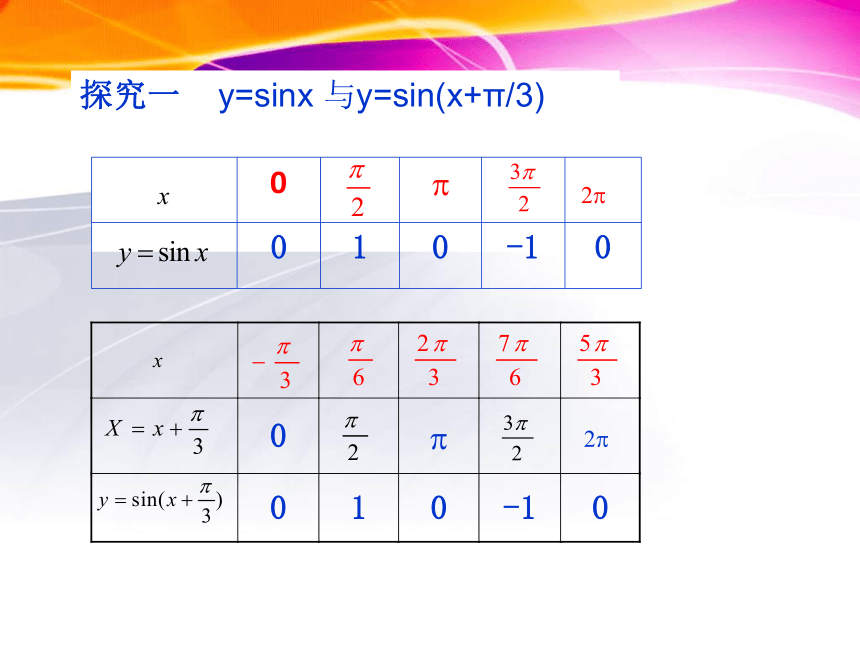
探究一: y=sinx 与y=sin(x+π/3)
探究三: y=sin(2x+π/3)与y=3sin(2x+π/3)
1组展示
3组展示
5组展示
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
0
0
3
0
-3
0
2
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
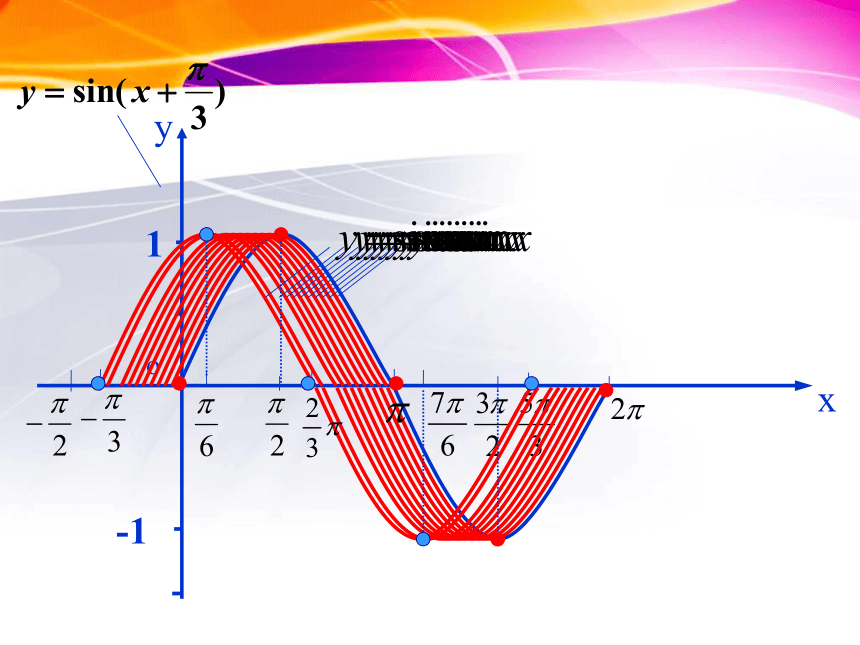
探究一 y=sinx 与y=sin(x+π/3)
1
-1
o
x
y
规律一、φ对y=sin(x+φ)的图象的影响
一般地,函数y=sin(x+φ),(φ≠0)的图象,可以看作是把y=sinx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位而得到.
练习:已知函数y=sinx的图象为C,为了得到函数
y=sin(x-π/4)的图象,只要把C上所有的点( )
(A)向右平行移动π/4个单位长度
(B)向左平行移动π/4个单位长度
1
A
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
探究二: y=sin(x+π/3)与y=sin(2x+π/3)
*
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sin(x+ )①
规律二、ω对y=sin(ωx+φ)的图象的影响
一般地,函数y=sin(ωx+φ)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω (纵坐标不变)而得到的.
练:2已知函数y=sin(x-π/4)的图象为C,为了得到函数 y=sin(x/3-π/4)的图象,只要把C上所有的点( )
(A)横坐标伸长到原来的3倍,纵坐标不变
(B)横坐标缩短到原来的1/3倍,纵坐标不变
(C)纵坐标伸长到原来的3倍,横坐标不变
(D)纵坐标缩短到原来的1/3倍,横坐标不变
A
0
0
1
0
-1
0
2
0
0
3
0
-3
0
2
探究三: y=sin(2x+π/3)与y=3sin(2x+π/3)
1
-1
2
-2
o
x
y
3
-3
y=sin(2x + )
y=3sin(2x+ )
一般地,函数y=Asin(ωx+φ)(A>0)的图象可以看作是把y=sin(ωx+φ)上所有点的纵坐标伸长(当A>1时)或缩短(当0规律三、A对y=Asin(ωx+φ)的图象的影响
参数φ, ω, A 对图象的影响
Φ:沿x轴平 移 |φ|个单位 ,
口诀: “左加” “右减”
ω: 横坐标伸长或缩短为原来的1/ω
A:纵坐标伸长或缩短为原来的A倍
例、如何由 变换得
的图象?
(二)探索y=Asin(ωx+φ)和y=sinx的图象关系
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
方法1:
y=sin(x+ )
y=sinx
关键 :如何由 图象变成
的图象?
◆思考:还有其他的变换方法吗?
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
探究:y=sin(2x)和y=sin(2x+π/3)图象关系
向左平移 个单位
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=sinx
y=sin2x
y=3sin(2x+ )
方法2:
如何由 图象变成
的图象?
你学到了哪些知识?
还有什么疑问?
作y=sinx(长度为2 的某闭区间)
y=sin(x+φ)
y=sinωx
y=sin(ωx+φ)
y=Asin(ωx+φ)的图象,先在一个周期闭区间上再扩充到R上
沿x轴平移 |φ|个单位
横坐标 变为1/ω
横坐标 变为1/ω
沿x轴平移 个单位
纵坐标 变为A倍
小结:y=Asin(ωx+φ)和y=sinx的图象关系
由 的图象经过怎样的
变换得到 的图象?
普通高中课程标准实验教科书必修④
函数y=Asin(ωx+φ)的图象
邯郸四中 杜瑞敏
1.“五点法”作y=sinx图象的“五点”指:
2.“五点法”作图的步骤:
列表,描点,成图
如何由函数y=sinx的图象变换得到函数y=Asin(ωx+φ)的图象
培养观察问题和探索问题的能力
(一)探索A,ω,φ对函数y=Asin(ωx+φ)(A>0, ω>0)图像的影响:
用“五点法”在同一坐标系画出下列几组函数(在一个周期的)图象,并说明它们之间的关系:
探究二: y=sin(x+π/3)与y=sin(2x+π/3)
探究一: y=sinx 与y=sin(x+π/3)
探究三: y=sin(2x+π/3)与y=3sin(2x+π/3)
1组展示
3组展示
5组展示
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
0
0
3
0
-3
0
2
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
探究一 y=sinx 与y=sin(x+π/3)
1
-1
o
x
y
规律一、φ对y=sin(x+φ)的图象的影响
一般地,函数y=sin(x+φ),(φ≠0)的图象,可以看作是把y=sinx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位而得到.
练习:已知函数y=sinx的图象为C,为了得到函数
y=sin(x-π/4)的图象,只要把C上所有的点( )
(A)向右平行移动π/4个单位长度
(B)向左平行移动π/4个单位长度
1
A
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
探究二: y=sin(x+π/3)与y=sin(2x+π/3)
*
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x + )②
y=sin(x+ )①
规律二、ω对y=sin(ωx+φ)的图象的影响
一般地,函数y=sin(ωx+φ)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω (纵坐标不变)而得到的.
练:2已知函数y=sin(x-π/4)的图象为C,为了得到函数 y=sin(x/3-π/4)的图象,只要把C上所有的点( )
(A)横坐标伸长到原来的3倍,纵坐标不变
(B)横坐标缩短到原来的1/3倍,纵坐标不变
(C)纵坐标伸长到原来的3倍,横坐标不变
(D)纵坐标缩短到原来的1/3倍,横坐标不变
A
0
0
1
0
-1
0
2
0
0
3
0
-3
0
2
探究三: y=sin(2x+π/3)与y=3sin(2x+π/3)
1
-1
2
-2
o
x
y
3
-3
y=sin(2x + )
y=3sin(2x+ )
一般地,函数y=Asin(ωx+φ)(A>0)的图象可以看作是把y=sin(ωx+φ)上所有点的纵坐标伸长(当A>1时)或缩短(当0
参数φ, ω, A 对图象的影响
Φ:沿x轴平 移 |φ|个单位 ,
口诀: “左加” “右减”
ω: 横坐标伸长或缩短为原来的1/ω
A:纵坐标伸长或缩短为原来的A倍
例、如何由 变换得
的图象?
(二)探索y=Asin(ωx+φ)和y=sinx的图象关系
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
方法1:
y=sin(x+ )
y=sinx
关键 :如何由 图象变成
的图象?
◆思考:还有其他的变换方法吗?
0
0
1
0
-1
0
2
0
0
1
0
-1
0
2
探究:y=sin(2x)和y=sin(2x+π/3)图象关系
向左平移 个单位
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=sinx
y=sin2x
y=3sin(2x+ )
方法2:
如何由 图象变成
的图象?
你学到了哪些知识?
还有什么疑问?
作y=sinx(长度为2 的某闭区间)
y=sin(x+φ)
y=sinωx
y=sin(ωx+φ)
y=Asin(ωx+φ)的图象,先在一个周期闭区间上再扩充到R上
沿x轴平移 |φ|个单位
横坐标 变为1/ω
横坐标 变为1/ω
沿x轴平移 个单位
纵坐标 变为A倍
小结:y=Asin(ωx+φ)和y=sinx的图象关系
由 的图象经过怎样的
变换得到 的图象?
