第二十七章 反比例函数复习课件 冀教版数学九年级上册(1)(18张PPT)
文档属性
| 名称 | 第二十七章 反比例函数复习课件 冀教版数学九年级上册(1)(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 891.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
冀教2011课标版九年级数学
第27章
反比例函数复习
1、请你任意写出一个反比例函数的解析式,并给出最简单的条件让大家求出你的函数解析式。
2、你的反比例函数还有其它的表示形式吗?
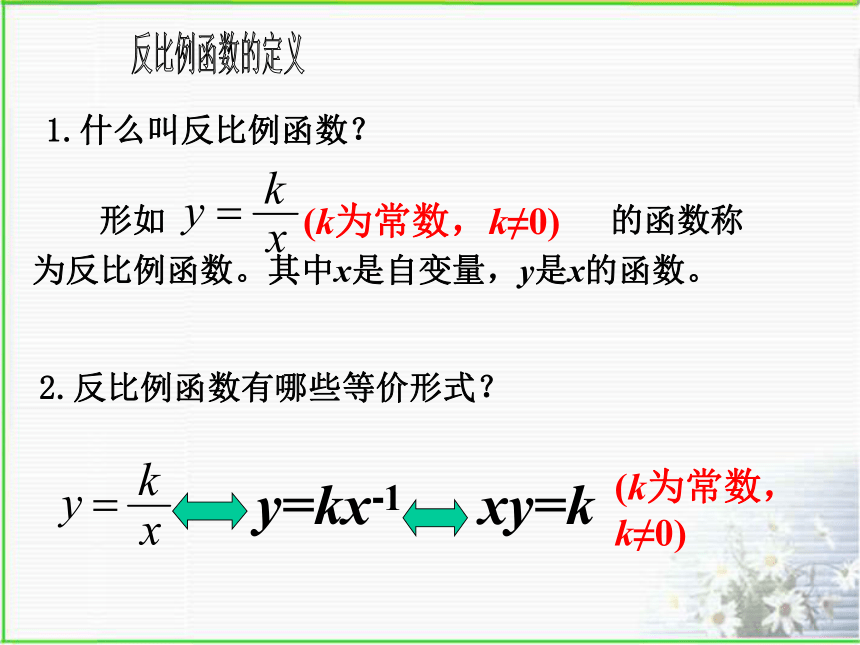
1.什么叫反比例函数?
形如
的函数称为反比例函数。其中x是自变量,y是x的函数。
(k为常数,k≠0)
2.反比例函数有哪些等价形式?
y=kx-1
xy=k
(k为常数,k≠0)
1、下列函数中哪些是反比例函数?
①
②
③
④
⑤
⑥
⑦
⑧
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
1
3x
y
=
x
1
xy=-2
3.下列的数表中分别给出了变量y与x之间的对应关系,其中是反比例函数关系的是(
).
x
1
2
3
4
y
6
8
9
7
x
1
2
3
4
y
8
5
4
3
x
1
2
3
4
y
5
8
7
6
x
1
2
3
4
y
1
A:
C:
D:
B:
D
2.
若
是反比例函数,
则m=______.
-2
那么下列各点中一定也在此图象上的点是(
)
4.若点(-m,n)在反比例函数
A.
(m,n)
B.
(-m,-n)
C.
(m,-n)
D.
(-n,-m)
的图象上,
C
同学们画出你所做的反比例函数的图象,并写出你所做的反比例函数图象的形状和性质,回答下列问题。
1、你做的图象与坐标轴有没有交点?为什么?图象的对称性如何?
2、请你从k的符号、图象的位置、增减性三个方面中选择一个描述你的反比例函数的特点,然后由另一个同学说出另外两个方面的内容。
函数
反比例函数
解析式
图象形状
k>0
位置
增减性
k<0
位置
增减性
双曲线
在每一个象限内y随x的增大而增大
双曲线两分支分别在
第一、第三象限
在每一个象限内y随x的增大而减小;
双曲线两分支分别在
第二、第四象限
1、在图中反比例函数
的图象大致是(
)
2、如果反比例函数
的图象位于第二、四象限,
那么m的范围为(
)
m>
D
3、在同一直角坐标系中,函数y=kx-k与?
的图象大致是(?????)
D
4、在反比例函数
2)将x1>x2
>0变为x1
>0
>x2,则y1与y2
的大小关系是
。
若x1
>
x2
>0,则y1与y2的大小关系是
。
的图象上有两点(x1,y1)、(x2,y2),
1)将x1>x2
>0变为0>x1>x2,则y1与y2
的大小关系是
。
变式训练:
y1
y1
>y2
y1
3)将x1>x2
>0变为x1>x2,则y1与y2
的大小关系是
。
0
x
B
A
5、过原点的一条直线与反比例函数
y=k/x
(k≠0)的图象分别交于A、B两点,若点A的坐标(a,b),
则点B的坐标为(
)
A.
(b,a)
B.
(-a,b)
C.
(-b,-a)
D.
(-a,-b)
D
6、如图,正比例函数与反比例函数的图象相交于A,B两点,点A坐标为(2,1),分别以A,B为圆心的圆与X轴相切,则图中两个阴影部分面积的和为(
)
请你在所作的反比函数图象上任取一点,由这一点分别向x轴,y轴作垂线,并计算构成的矩形的面积。
1、叙述自己的解析式,由另一个学生说出矩形面积。
2、说出矩形面积及取点所在象限,另一个学生说出解析式。
如果改为由这一点向x轴或y轴作垂线,并与原点相连,构成一个直角三角形,直角三角形的面积与矩形面积有什么关系呢?
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
如图点A为反比例函数y=1/x的图象上一点,点B在x轴上,且OA=BA,则三角形AOB的面积为(
)
O
x
y
A
B
c
1
如图,在直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数y=-2/x(x<0)的图象与点B,交函数y=6/x(x>0)的图象与点C,过点C作y轴的平行线交BD的延长线与点D.
(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比。
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比。
(3)对于动点A,求四边形AODC的面积。
B
A
C
O
y
x
D
y=-2/x
y=6/x
如图,在直角坐标系中,直角三角形ABC位于第一象限,两条直角边BC,BA分别平行于x轴,y轴,点A的坐标为(1,1),AB=2,BC=4.
求点C坐标和AC边所在直线的解析式。
若反比例函数y=m/x(x>0)的图象经过点B,求m的值。
若反比例函数y=m/x(x>0)的图象与AC边有公共点,请直接写出m的取值范围。
y
x
o
A
B
C
冀教2011课标版九年级数学
第27章
反比例函数复习
1、请你任意写出一个反比例函数的解析式,并给出最简单的条件让大家求出你的函数解析式。
2、你的反比例函数还有其它的表示形式吗?
1.什么叫反比例函数?
形如
的函数称为反比例函数。其中x是自变量,y是x的函数。
(k为常数,k≠0)
2.反比例函数有哪些等价形式?
y=kx-1
xy=k
(k为常数,k≠0)
1、下列函数中哪些是反比例函数?
①
②
③
④
⑤
⑥
⑦
⑧
y
=
3x-1
y
=
2x2
y
=
2x
3
y
=
x
1
y
=
3x
y
=
1
3x
y
=
x
1
xy=-2
3.下列的数表中分别给出了变量y与x之间的对应关系,其中是反比例函数关系的是(
).
x
1
2
3
4
y
6
8
9
7
x
1
2
3
4
y
8
5
4
3
x
1
2
3
4
y
5
8
7
6
x
1
2
3
4
y
1
A:
C:
D:
B:
D
2.
若
是反比例函数,
则m=______.
-2
那么下列各点中一定也在此图象上的点是(
)
4.若点(-m,n)在反比例函数
A.
(m,n)
B.
(-m,-n)
C.
(m,-n)
D.
(-n,-m)
的图象上,
C
同学们画出你所做的反比例函数的图象,并写出你所做的反比例函数图象的形状和性质,回答下列问题。
1、你做的图象与坐标轴有没有交点?为什么?图象的对称性如何?
2、请你从k的符号、图象的位置、增减性三个方面中选择一个描述你的反比例函数的特点,然后由另一个同学说出另外两个方面的内容。
函数
反比例函数
解析式
图象形状
k>0
位置
增减性
k<0
位置
增减性
双曲线
在每一个象限内y随x的增大而增大
双曲线两分支分别在
第一、第三象限
在每一个象限内y随x的增大而减小;
双曲线两分支分别在
第二、第四象限
1、在图中反比例函数
的图象大致是(
)
2、如果反比例函数
的图象位于第二、四象限,
那么m的范围为(
)
m>
D
3、在同一直角坐标系中,函数y=kx-k与?
的图象大致是(?????)
D
4、在反比例函数
2)将x1>x2
>0变为x1
>0
>x2,则y1与y2
的大小关系是
。
若x1
>
x2
>0,则y1与y2的大小关系是
。
的图象上有两点(x1,y1)、(x2,y2),
1)将x1>x2
>0变为0>x1>x2,则y1与y2
的大小关系是
。
变式训练:
y1
>y2
y1
>0变为x1>x2,则y1与y2
的大小关系是
。
0
x
B
A
5、过原点的一条直线与反比例函数
y=k/x
(k≠0)的图象分别交于A、B两点,若点A的坐标(a,b),
则点B的坐标为(
)
A.
(b,a)
B.
(-a,b)
C.
(-b,-a)
D.
(-a,-b)
D
6、如图,正比例函数与反比例函数的图象相交于A,B两点,点A坐标为(2,1),分别以A,B为圆心的圆与X轴相切,则图中两个阴影部分面积的和为(
)
请你在所作的反比函数图象上任取一点,由这一点分别向x轴,y轴作垂线,并计算构成的矩形的面积。
1、叙述自己的解析式,由另一个学生说出矩形面积。
2、说出矩形面积及取点所在象限,另一个学生说出解析式。
如果改为由这一点向x轴或y轴作垂线,并与原点相连,构成一个直角三角形,直角三角形的面积与矩形面积有什么关系呢?
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
如图点A为反比例函数y=1/x的图象上一点,点B在x轴上,且OA=BA,则三角形AOB的面积为(
)
O
x
y
A
B
c
1
如图,在直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数y=-2/x(x<0)的图象与点B,交函数y=6/x(x>0)的图象与点C,过点C作y轴的平行线交BD的延长线与点D.
(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比。
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比。
(3)对于动点A,求四边形AODC的面积。
B
A
C
O
y
x
D
y=-2/x
y=6/x
如图,在直角坐标系中,直角三角形ABC位于第一象限,两条直角边BC,BA分别平行于x轴,y轴,点A的坐标为(1,1),AB=2,BC=4.
求点C坐标和AC边所在直线的解析式。
若反比例函数y=m/x(x>0)的图象经过点B,求m的值。
若反比例函数y=m/x(x>0)的图象与AC边有公共点,请直接写出m的取值范围。
y
x
o
A
B
C
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
