2.2.1《直线和平面平行判定》(新人教A版必修2)
文档属性
| 名称 | 2.2.1《直线和平面平行判定》(新人教A版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-30 15:36:41 | ||
图片预览







文档简介
(共30张PPT)
2.2.1 直线与平面平行的判定
人教A版普通高中课程标准实验教科书数学必修2
山东省无棣县二中 孙瑞海
(第一课时)
1
教
材
分
析
3
教
学
目
标
分
析
4
教
法
学
法
分
析
5
教
学
过
程
分
析
说
课
流
程
2
学
情
分
析
6
设
计
说
明
本节课主要学习直线和平面平行的定义,判定定理以及初步应用。线面平行的定义是线面平行最基本的判定方法和性质,它是探究线面平行判定定理的基础,线面平行的判定充分体现了线线平行和线面平行之间的转化,它既是后面学习面面平行的基础,又是连接线线平行和面面平行的纽带。所以本节课起着承上启下的作用。本节课的学习对培养学生空间感与逻辑推理其重要作用。
1、
教
材
的
地
位
和
作
用
一、教材分析
教学重点:通过直观感知、自主探索,归纳出直线和平面平行的判定及其应用。
教学难点:直线和平面平行的判定定理的探索过程及其应用。
解决问题的关键是:证明平面外的一条直线和平面内的一条直线平行。
2、
重
、难点及突破关键
二、学情分析
学生已经掌握了平面内证明线线平行的方法,前一节又刚刚学过在空间中直线与直线的位置关系,对空间概念的建立有一定基础 ,但是学生的抽象概括能力,空间想象力还有待提高,线面平行的定义比较抽象,要让学生体会“与平面无公共点”有一定困难,线面平行的判定的发现有一定隐蔽性。
知识方面:通过直观感知——观察——操作确认的认识方法理解并掌握直线与平面平行的判定定理,掌握直线与平面平行的画法并能准确使用数学符号语言、文字语言表述判定定理。
能力方面:培养学生观察、探究、发现的能力和空间想象能力、逻辑思维能力。让学生在观察、探究、发现中学习,在自主合作、交流中学习,体验学习的乐趣,增强自信心,树立积极的学习态度,提高学习的自我效能感。
情感方面:让学生亲身经历数学研究的过程,体验探索的乐趣,增强学习数学的兴趣。
三、教学目标
教法:根据本节内容较抽象,学生不易理解的特点,本节教学采用启发式教学,辅以观察法、发现法、练习法、讲解法。采用这种方法的原因是高一学生的空间想象能力比较差,只能通过对实物的观察及一定的练习才能掌握本节知识。
学法指导:通过对直观教具的观察,教会学生观察——猜想——证明 的学习方法,让学生进一步了解反证法的实质及“转化”的数学思想方法,在教学中培养学生的逻辑思维能力和空间想象能力,并在教学中逐步提高学生论证问题的能力。
四、教法学法及教学手段分析
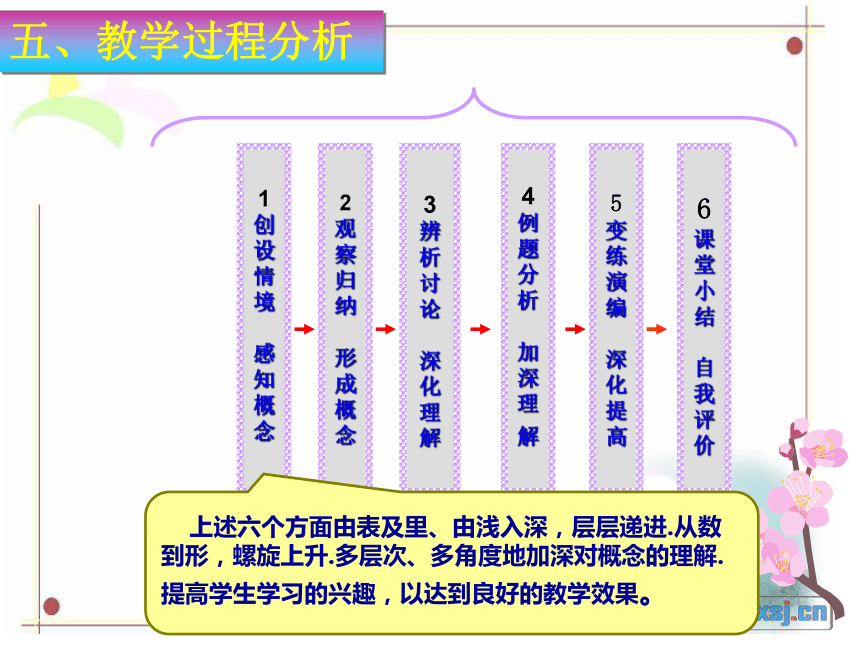
1
创
设
情
境
感
知
概
念
2
观
察
归
纳
形
成
概
念
5
变
练
演
编
深
化
提
高
3
辨
析
讨
论
深
化
理
解
6
课
堂
小
结
自
我
评
价
4
例
题
分
析
加
深
理
解
上述六个方面由表及里、由浅入深,层层递进.从数到形,螺旋上升.多层次、多角度地加深对概念的理解. 提高学生学习的兴趣,以达到良好的教学效果。
五、教学过程分析
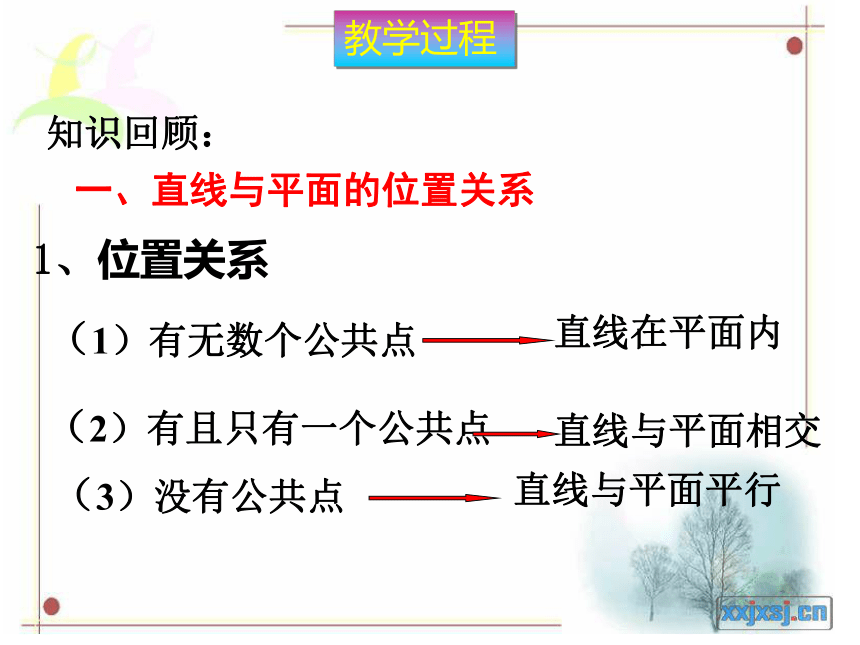
一、直线与平面的位置关系
(1)有无数个公共点
(2)有且只有一个公共点
(3)没有公共点
直线在平面内
直线与平面相交
直线与平面平行
1、位置关系
知识回顾:
教学过程
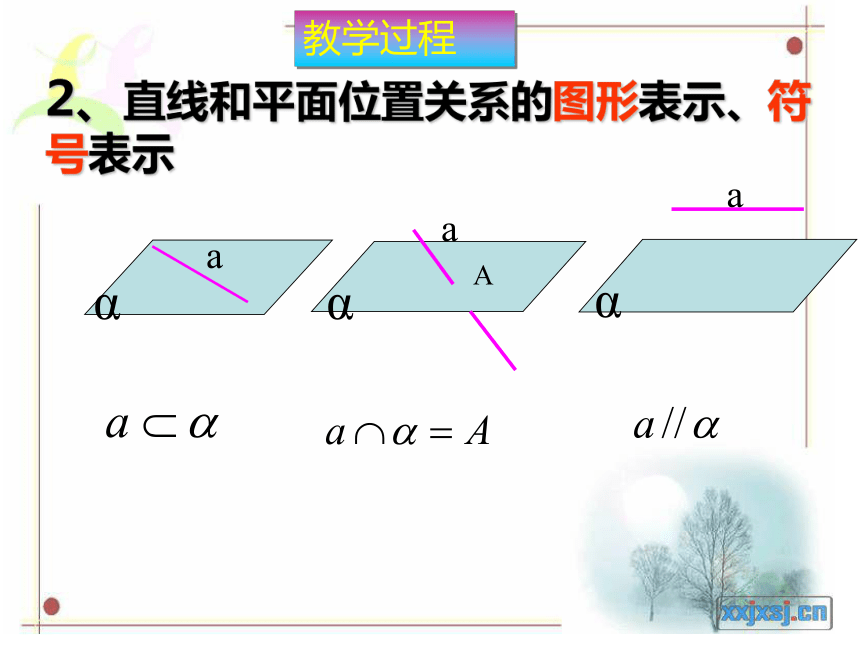
2、直线和平面位置关系的图形表示、符号表示
α
a
α
A
a
a
α
教学过程
问题1:
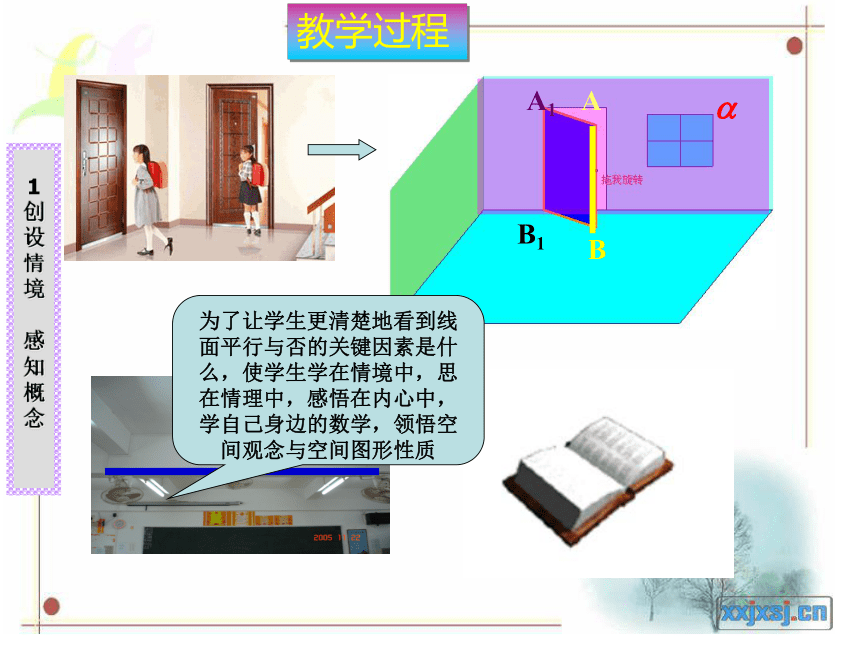
把门打开,门上靠近把手的边与墙面所在的平面有何关系?
在黑板的上方装一盏日光灯,怎样才能使日光灯与天花板平行呢
问题2:
问题3:
将课本的一边紧贴桌面,沿着这条边
转动课本,课本的上边缘与桌面的关
系如何呢?
教学过程
1
创
设
情
境
感
知
概
念
设计目的:以具体例子理解直线与平面平行
教学过程
A1
B1
A
B
天花板平面
1
创
设
情
境
感
知
概
念
为了让学生更清楚地看到线面平行与否的关键因素是什么,使学生学在情境中,思在情理中,感悟在内心中,学自己身边的数学,领悟空间观念与空间图形性质
球场地面
教学过程
思考:如何判断一条直线与一个平面平行?
1
创
设
情
境
感
知
概
念
·
感受生活中线面平行的例子
提出本节学习内容,留下悬念,激发探索求知欲望
b
a
a
α
讨论:能否用平面外一条直线平行于平面内直线,来判断这条直线与这个平面平行呢?
教学过程
2
观
察
归
纳
形
成
概
念
通过探索,直观感知,操作确认给出判定定理
b
a
b
a∥b
a
a ∥
如果平面外的一条直线和此平面内的一条直线平行,那么这条直线和这个平面平行.
直线和平面平行的判定定理:
2
观
察
归
纳
形
成
概
念
分组讨论:
判断下列命题是否正确,若不正确,请用图形语言或模型加以表达
(1)
(2)
(3)
3
辨
析
讨
论
深
化
理
解
判定定理的三个条件缺一不可
b
a∥b
a
a ∥
简记为:内外线线平行
线面平行
(平面化)
(空间问题)
3
辨
析
讨
论
深
化
理
解
1、判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.
(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )
(2)如果直线a、b和平面α 满足a ∥ α,
b ∥ α,那么a ∥ b ;( )
(3)如果直线a、b和平面α 满足a ∥ b,a ∥α,
b α, 那么 b ∥ α;( )
(4)过平面外一点和这个平面平行的直线只有一条.( )
定理运用、辨析:
强调定理中三个条件的重要性让学生想象的空间更广阔些
定理运用、辨析:
理解直线与平面平行的定义,掌握直线与平面平行的判定.
F
例1、证明:空间四边形相邻两边的中点的连线平行于经过另两边的平面.
A
B
C
D
E
已知:如图空间四边形ABCD中,E、F分别为AB、AD的中点.
求证:EF//平面BCD.
4
例
题
分
析
加
深
理
解
教学过程
使学生进一步了解空间四边形的概念画法,将定理应用于例题中三条件一一理解清楚
已知:如图空间四边形ABCD中,E、F分别为AB、AD的中点.
求证:EF//平面BCD.
证明:连接BD
因为 AE=EB,AF=FD,
A
B
C
D
E
F
由直线与平面平行的判定定理得
所以
又因为
EF//BD
教学过程
4
例
题
分
析
加
深
理
解
1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCD
变式1:
A
B
C
D
E
F
教学过程
5
变
练
演
编
深
化
提
高
变式2:
A
B
C
D
F
O
E
2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF。
分析:连结OF,
可知OF为
△ABE的中位线,所以得到AB//OF.
教学过程
5
变
练
演
编
深
化
提
高
设计二个变式训练,目的是通过问题探究、讨论,及时巩固定理,运用定理,培养学生的识图能力与逻辑推理能力,真正起到举一反三。
∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,
B
D
F
O
连结OF,
A
C
E
教学过程
5
变
练
演
编
深
化
提
高
证明:
变式2:
1.如图,长方体 中,
(1)与AB平行的平面是 ;
(2)与 平行的平面是 ;
(3)与AD平行的平面是 ;
平面
平面
平面
平面
平面
平面
随堂练习
O
A
D
A1
C
B
D1
B1
C1
E
随堂练习:
课本P56: 2. 如下图,正方体AC1中,E为DD1的中点,试判断BD1与平面AEC的位置关系,并说明理由。
根据空间问题平面化的思想,因此把找空间平行直线问题转化为找平行四边形或三角形中位线问题,这样就自然想到了找中点。平行问题找中点解决是个好途径好方法
能力提高
V
B
C
A
.
E
F
G
一木块如图所示,点P在平面VAC内,过点P将木块锯开,使截面平行于直线VB和AC,应该怎样画线?
作法: 1)过点P作EF//AC 分别交V C 、VA于E、F点;
2 )分别过E作EH//VB交BC于H点,过F点作FG//VB交AB于G点;
3)最后连接GH;
平面EFGH即为所求的截面.
H
P
(1)课本P62练习3
(2)思考题:如图:在三角形ABC所在平面外有一点V,M、N分别是VC和AC上的点,过MN作平面平行于BC,画出这个平面
与其它各面的交线,
并说明理由.
N
V
B
M
A
C
作业
【课堂小结】
(1)线面平行的判定定理
线线平行
线面平行
(将空间问题转化为平面问题)
(2)线面平行的判定方法;
平行移动法
平行四边形法
中位线法
6
课
堂
小
结
自
我
评
价
注意六个字:
(1)面外
(2)面内 (3)平行
关键是找平行
1、如何证明面面平行呢?
课外探讨:
2、如图,已知有公共边AB的两个全等矩形ABCD和ABEF不在同一个平面内,P、Q对角线AE、BD上的动点。
当P、Q满足什么条件时,
PQ∥平面CBE?
作业: A组第4题、P63页B组第3题
2.2.1 直线与平面平行的判定
人教A版普通高中课程标准实验教科书数学必修2
山东省无棣县二中 孙瑞海
(第一课时)
1
教
材
分
析
3
教
学
目
标
分
析
4
教
法
学
法
分
析
5
教
学
过
程
分
析
说
课
流
程
2
学
情
分
析
6
设
计
说
明
本节课主要学习直线和平面平行的定义,判定定理以及初步应用。线面平行的定义是线面平行最基本的判定方法和性质,它是探究线面平行判定定理的基础,线面平行的判定充分体现了线线平行和线面平行之间的转化,它既是后面学习面面平行的基础,又是连接线线平行和面面平行的纽带。所以本节课起着承上启下的作用。本节课的学习对培养学生空间感与逻辑推理其重要作用。
1、
教
材
的
地
位
和
作
用
一、教材分析
教学重点:通过直观感知、自主探索,归纳出直线和平面平行的判定及其应用。
教学难点:直线和平面平行的判定定理的探索过程及其应用。
解决问题的关键是:证明平面外的一条直线和平面内的一条直线平行。
2、
重
、难点及突破关键
二、学情分析
学生已经掌握了平面内证明线线平行的方法,前一节又刚刚学过在空间中直线与直线的位置关系,对空间概念的建立有一定基础 ,但是学生的抽象概括能力,空间想象力还有待提高,线面平行的定义比较抽象,要让学生体会“与平面无公共点”有一定困难,线面平行的判定的发现有一定隐蔽性。
知识方面:通过直观感知——观察——操作确认的认识方法理解并掌握直线与平面平行的判定定理,掌握直线与平面平行的画法并能准确使用数学符号语言、文字语言表述判定定理。
能力方面:培养学生观察、探究、发现的能力和空间想象能力、逻辑思维能力。让学生在观察、探究、发现中学习,在自主合作、交流中学习,体验学习的乐趣,增强自信心,树立积极的学习态度,提高学习的自我效能感。
情感方面:让学生亲身经历数学研究的过程,体验探索的乐趣,增强学习数学的兴趣。
三、教学目标
教法:根据本节内容较抽象,学生不易理解的特点,本节教学采用启发式教学,辅以观察法、发现法、练习法、讲解法。采用这种方法的原因是高一学生的空间想象能力比较差,只能通过对实物的观察及一定的练习才能掌握本节知识。
学法指导:通过对直观教具的观察,教会学生观察——猜想——证明 的学习方法,让学生进一步了解反证法的实质及“转化”的数学思想方法,在教学中培养学生的逻辑思维能力和空间想象能力,并在教学中逐步提高学生论证问题的能力。
四、教法学法及教学手段分析
1
创
设
情
境
感
知
概
念
2
观
察
归
纳
形
成
概
念
5
变
练
演
编
深
化
提
高
3
辨
析
讨
论
深
化
理
解
6
课
堂
小
结
自
我
评
价
4
例
题
分
析
加
深
理
解
上述六个方面由表及里、由浅入深,层层递进.从数到形,螺旋上升.多层次、多角度地加深对概念的理解. 提高学生学习的兴趣,以达到良好的教学效果。
五、教学过程分析
一、直线与平面的位置关系
(1)有无数个公共点
(2)有且只有一个公共点
(3)没有公共点
直线在平面内
直线与平面相交
直线与平面平行
1、位置关系
知识回顾:
教学过程
2、直线和平面位置关系的图形表示、符号表示
α
a
α
A
a
a
α
教学过程
问题1:
把门打开,门上靠近把手的边与墙面所在的平面有何关系?
在黑板的上方装一盏日光灯,怎样才能使日光灯与天花板平行呢
问题2:
问题3:
将课本的一边紧贴桌面,沿着这条边
转动课本,课本的上边缘与桌面的关
系如何呢?
教学过程
1
创
设
情
境
感
知
概
念
设计目的:以具体例子理解直线与平面平行
教学过程
A1
B1
A
B
天花板平面
1
创
设
情
境
感
知
概
念
为了让学生更清楚地看到线面平行与否的关键因素是什么,使学生学在情境中,思在情理中,感悟在内心中,学自己身边的数学,领悟空间观念与空间图形性质
球场地面
教学过程
思考:如何判断一条直线与一个平面平行?
1
创
设
情
境
感
知
概
念
·
感受生活中线面平行的例子
提出本节学习内容,留下悬念,激发探索求知欲望
b
a
a
α
讨论:能否用平面外一条直线平行于平面内直线,来判断这条直线与这个平面平行呢?
教学过程
2
观
察
归
纳
形
成
概
念
通过探索,直观感知,操作确认给出判定定理
b
a
b
a∥b
a
a ∥
如果平面外的一条直线和此平面内的一条直线平行,那么这条直线和这个平面平行.
直线和平面平行的判定定理:
2
观
察
归
纳
形
成
概
念
分组讨论:
判断下列命题是否正确,若不正确,请用图形语言或模型加以表达
(1)
(2)
(3)
3
辨
析
讨
论
深
化
理
解
判定定理的三个条件缺一不可
b
a∥b
a
a ∥
简记为:内外线线平行
线面平行
(平面化)
(空间问题)
3
辨
析
讨
论
深
化
理
解
1、判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.
(1)如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )
(2)如果直线a、b和平面α 满足a ∥ α,
b ∥ α,那么a ∥ b ;( )
(3)如果直线a、b和平面α 满足a ∥ b,a ∥α,
b α, 那么 b ∥ α;( )
(4)过平面外一点和这个平面平行的直线只有一条.( )
定理运用、辨析:
强调定理中三个条件的重要性让学生想象的空间更广阔些
定理运用、辨析:
理解直线与平面平行的定义,掌握直线与平面平行的判定.
F
例1、证明:空间四边形相邻两边的中点的连线平行于经过另两边的平面.
A
B
C
D
E
已知:如图空间四边形ABCD中,E、F分别为AB、AD的中点.
求证:EF//平面BCD.
4
例
题
分
析
加
深
理
解
教学过程
使学生进一步了解空间四边形的概念画法,将定理应用于例题中三条件一一理解清楚
已知:如图空间四边形ABCD中,E、F分别为AB、AD的中点.
求证:EF//平面BCD.
证明:连接BD
因为 AE=EB,AF=FD,
A
B
C
D
E
F
由直线与平面平行的判定定理得
所以
又因为
EF//BD
教学过程
4
例
题
分
析
加
深
理
解
1.如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCD
变式1:
A
B
C
D
E
F
教学过程
5
变
练
演
编
深
化
提
高
变式2:
A
B
C
D
F
O
E
2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF。
分析:连结OF,
可知OF为
△ABE的中位线,所以得到AB//OF.
教学过程
5
变
练
演
编
深
化
提
高
设计二个变式训练,目的是通过问题探究、讨论,及时巩固定理,运用定理,培养学生的识图能力与逻辑推理能力,真正起到举一反三。
∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又AF=FE,
∴AB//OF,
B
D
F
O
连结OF,
A
C
E
教学过程
5
变
练
演
编
深
化
提
高
证明:
变式2:
1.如图,长方体 中,
(1)与AB平行的平面是 ;
(2)与 平行的平面是 ;
(3)与AD平行的平面是 ;
平面
平面
平面
平面
平面
平面
随堂练习
O
A
D
A1
C
B
D1
B1
C1
E
随堂练习:
课本P56: 2. 如下图,正方体AC1中,E为DD1的中点,试判断BD1与平面AEC的位置关系,并说明理由。
根据空间问题平面化的思想,因此把找空间平行直线问题转化为找平行四边形或三角形中位线问题,这样就自然想到了找中点。平行问题找中点解决是个好途径好方法
能力提高
V
B
C
A
.
E
F
G
一木块如图所示,点P在平面VAC内,过点P将木块锯开,使截面平行于直线VB和AC,应该怎样画线?
作法: 1)过点P作EF//AC 分别交V C 、VA于E、F点;
2 )分别过E作EH//VB交BC于H点,过F点作FG//VB交AB于G点;
3)最后连接GH;
平面EFGH即为所求的截面.
H
P
(1)课本P62练习3
(2)思考题:如图:在三角形ABC所在平面外有一点V,M、N分别是VC和AC上的点,过MN作平面平行于BC,画出这个平面
与其它各面的交线,
并说明理由.
N
V
B
M
A
C
作业
【课堂小结】
(1)线面平行的判定定理
线线平行
线面平行
(将空间问题转化为平面问题)
(2)线面平行的判定方法;
平行移动法
平行四边形法
中位线法
6
课
堂
小
结
自
我
评
价
注意六个字:
(1)面外
(2)面内 (3)平行
关键是找平行
1、如何证明面面平行呢?
课外探讨:
2、如图,已知有公共边AB的两个全等矩形ABCD和ABEF不在同一个平面内,P、Q对角线AE、BD上的动点。
当P、Q满足什么条件时,
PQ∥平面CBE?
作业: A组第4题、P63页B组第3题
