2.3《解三角形的实际应用举例》(北师大版必修5)
文档属性
| 名称 | 2.3《解三角形的实际应用举例》(北师大版必修5) |  | |
| 格式 | zip | ||
| 文件大小 | 974.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-30 15:36:41 | ||
图片预览






文档简介
(共21张PPT)
北师大版
解斜三角形
复习、请回答下列问题
(1)解斜三角形的主要理论依据是什么?
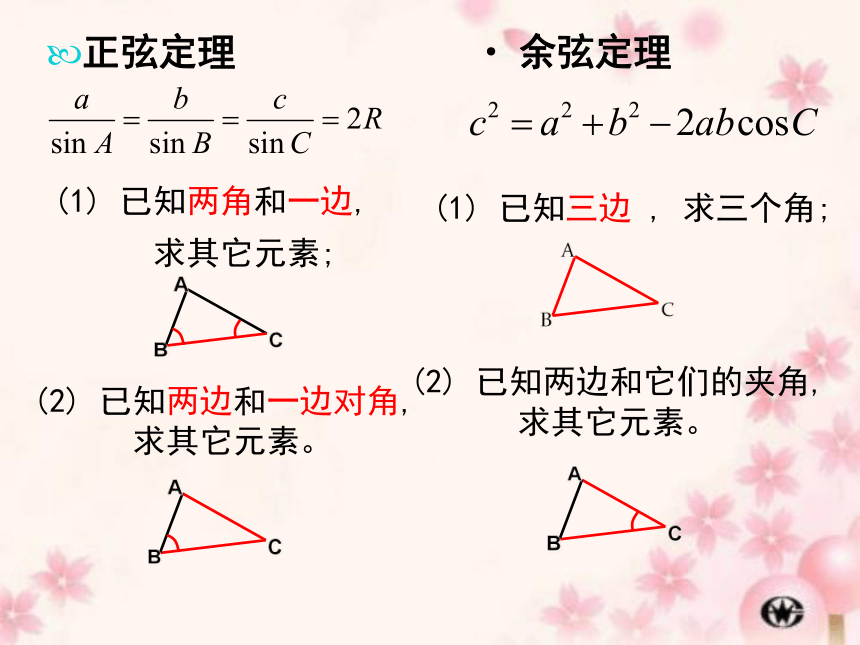
正弦定理
余弦定理
解斜三角形
复习、请回答下列问题
(1)解斜三角形的主要理论依据是什么?
(2)关于解斜三角形,你掌握了哪几种类型?
正弦定理
余弦定理
(1) 已知两角和一边,
求其它元素;
已知三边 , 求三个角;
A
B
C
(2) 已知两边和一边对角,
求其它元素。
(2) 已知两边和它们的夹角,
求其它元素。
A
B
C
A
B
C
A
B
C
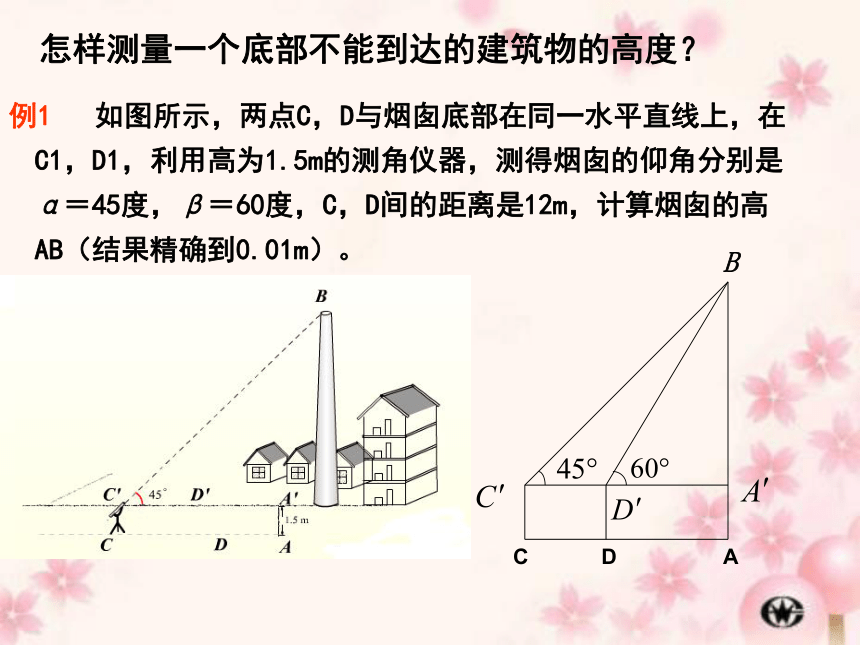
例1 如图所示,两点C,D与烟囱底部在同一水平直线上,在C1,D1,利用高为1.5m的测角仪器,测得烟囱的仰角分别是α=45度,β=60度,C,D间的距离是12m,计算烟囱的高AB(结果精确到0.01m)。
B
怎样测量一个底部不能到达的建筑物的高度?
C
D
A
A
B
C
D
答:烟囱的高约为21.23米
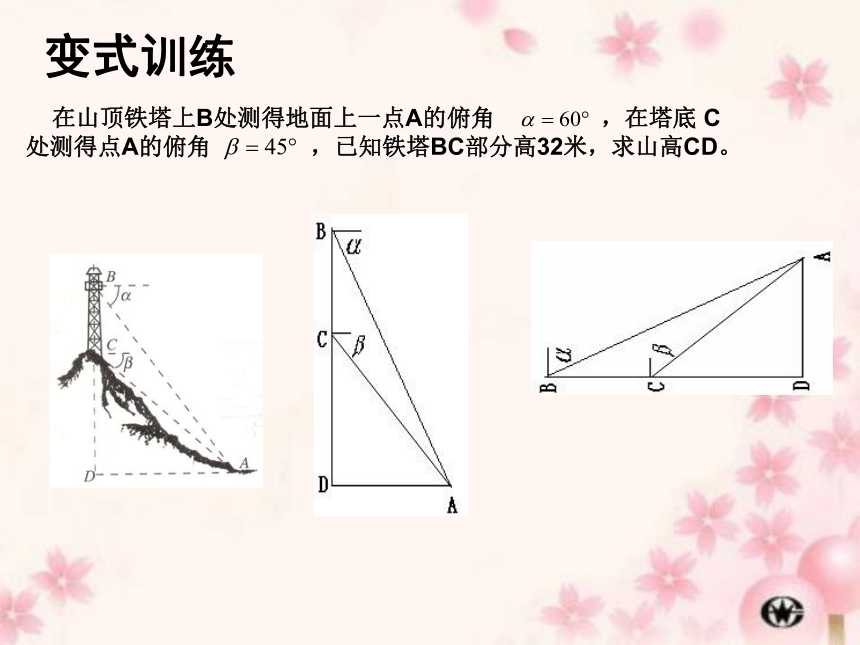
变式训练
在山顶铁塔上B处测得地面上一点A的俯角 ,在塔底 C 处测得点A的俯角 ,已知铁塔BC部分高32米,求山高CD。
解:在△ABC中,∠ABC=30°,
∠ACB =135°,
∴∠CAB =180° -(∠ACB+∠ABC)
=180°-(135°+30°)=15°
又BC=32,
由正弦定理
得
答:山高为 米。
例2 自动卸货汽车采用液压机构,设计时需要计算油泵顶杠BC的长度,如图所示,已知车厢的最大仰角为60 (指车厢AC与水平线夹角),油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6 20 ,AC长为1.40m,计算BC的长度(结果精确到0.01m)。
解 :
由余弦定理,得
BC2=AB2+AC2-2AB·ACcosA
=1.952+1.402-2×1.95×1.40cos 66 20
≈3.571
所以 BC≈1.89(m)
答:BC的长度约为1.89米
讨论:
怎样测量平面上两个不能到达的地方之间的距离?
①两点间不能到达,又不能相互看到。
A
B
C
需要测量CB、CA的长和角C的大小,由余弦定理,
可求得AB的长。
②两点间不能到达,但能相互看到。
C
B
A
需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,
可求边AB的长。
③两点都不能到达,但两点都可以看见。
A
B
C
D
AD?
BD?
角ADB?
正弦定理
正弦定理
求AB?
(余弦定理)
练习:
1. 有一长为10m的斜坡,它的倾斜角是 ,在不改变坡高和坡顶的前提下通过加长坡面的方法将它的倾斜角改为 ,则坡底要延伸( )
A 5m B10m C m D m
A
B
C
D
10
解析:
答案:C
2、海面上有A、B、C三个顶塔,AB =10海里,从A望B和C成 视角,从B望C和A成 视角,则BC等于多少海里?
A
B
C
10
解析:
3、如图所示,在加工缝纫机挑线杆时,需要计算A、C两孔中心的距离,已知BC=60.5毫米,AB=15.8毫米, 则AC等于多少毫米?(保留3个有效数字)
A
B
C
解析:
4、在一个20米高的楼顶测得对面一塔顶的仰角 为 ,塔底的俯角为 ,则塔高为多少米?
C
A
M
B
D
20
解析:
设AB为楼,CD为塔,AM为水平线,则有AB=20
所以,
小结:
通过解三角行解决实际问题的一般步骤:
(1)分析:理解题意,画出示意图。
(2)建模:把已知量与求解量集中在一个三角形中。
(3)求解:运用正弦定理和余弦定理有顺序的解三角形
(4)检验:检验所求的解是否符合实际意义,从而得出 实际问题的解
实际问题
数学问题
数学问题的解
实际问题的解
作业:
课本62页 习题2-3
A组 第3、4小题
谢谢指导
北师大版
解斜三角形
复习、请回答下列问题
(1)解斜三角形的主要理论依据是什么?
正弦定理
余弦定理
解斜三角形
复习、请回答下列问题
(1)解斜三角形的主要理论依据是什么?
(2)关于解斜三角形,你掌握了哪几种类型?
正弦定理
余弦定理
(1) 已知两角和一边,
求其它元素;
已知三边 , 求三个角;
A
B
C
(2) 已知两边和一边对角,
求其它元素。
(2) 已知两边和它们的夹角,
求其它元素。
A
B
C
A
B
C
A
B
C
例1 如图所示,两点C,D与烟囱底部在同一水平直线上,在C1,D1,利用高为1.5m的测角仪器,测得烟囱的仰角分别是α=45度,β=60度,C,D间的距离是12m,计算烟囱的高AB(结果精确到0.01m)。
B
怎样测量一个底部不能到达的建筑物的高度?
C
D
A
A
B
C
D
答:烟囱的高约为21.23米
变式训练
在山顶铁塔上B处测得地面上一点A的俯角 ,在塔底 C 处测得点A的俯角 ,已知铁塔BC部分高32米,求山高CD。
解:在△ABC中,∠ABC=30°,
∠ACB =135°,
∴∠CAB =180° -(∠ACB+∠ABC)
=180°-(135°+30°)=15°
又BC=32,
由正弦定理
得
答:山高为 米。
例2 自动卸货汽车采用液压机构,设计时需要计算油泵顶杠BC的长度,如图所示,已知车厢的最大仰角为60 (指车厢AC与水平线夹角),油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6 20 ,AC长为1.40m,计算BC的长度(结果精确到0.01m)。
解 :
由余弦定理,得
BC2=AB2+AC2-2AB·ACcosA
=1.952+1.402-2×1.95×1.40cos 66 20
≈3.571
所以 BC≈1.89(m)
答:BC的长度约为1.89米
讨论:
怎样测量平面上两个不能到达的地方之间的距离?
①两点间不能到达,又不能相互看到。
A
B
C
需要测量CB、CA的长和角C的大小,由余弦定理,
可求得AB的长。
②两点间不能到达,但能相互看到。
C
B
A
需要测量BC的长、角B和角C的大小,由三角形的内角和,求出角A然后由正弦定理,
可求边AB的长。
③两点都不能到达,但两点都可以看见。
A
B
C
D
AD?
BD?
角ADB?
正弦定理
正弦定理
求AB?
(余弦定理)
练习:
1. 有一长为10m的斜坡,它的倾斜角是 ,在不改变坡高和坡顶的前提下通过加长坡面的方法将它的倾斜角改为 ,则坡底要延伸( )
A 5m B10m C m D m
A
B
C
D
10
解析:
答案:C
2、海面上有A、B、C三个顶塔,AB =10海里,从A望B和C成 视角,从B望C和A成 视角,则BC等于多少海里?
A
B
C
10
解析:
3、如图所示,在加工缝纫机挑线杆时,需要计算A、C两孔中心的距离,已知BC=60.5毫米,AB=15.8毫米, 则AC等于多少毫米?(保留3个有效数字)
A
B
C
解析:
4、在一个20米高的楼顶测得对面一塔顶的仰角 为 ,塔底的俯角为 ,则塔高为多少米?
C
A
M
B
D
20
解析:
设AB为楼,CD为塔,AM为水平线,则有AB=20
所以,
小结:
通过解三角行解决实际问题的一般步骤:
(1)分析:理解题意,画出示意图。
(2)建模:把已知量与求解量集中在一个三角形中。
(3)求解:运用正弦定理和余弦定理有顺序的解三角形
(4)检验:检验所求的解是否符合实际意义,从而得出 实际问题的解
实际问题
数学问题
数学问题的解
实际问题的解
作业:
课本62页 习题2-3
A组 第3、4小题
谢谢指导
