4.8《函数y=A图像》(北师大版必修4)
文档属性
| 名称 | 4.8《函数y=A图像》(北师大版必修4) |  | |
| 格式 | zip | ||
| 文件大小 | 418.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-30 15:36:41 | ||
图片预览






文档简介
(共26张PPT)
§4.8y=Asin( x+ )+B
( 、A>0且≠1)的图象
北师大版数学必修四高一年级
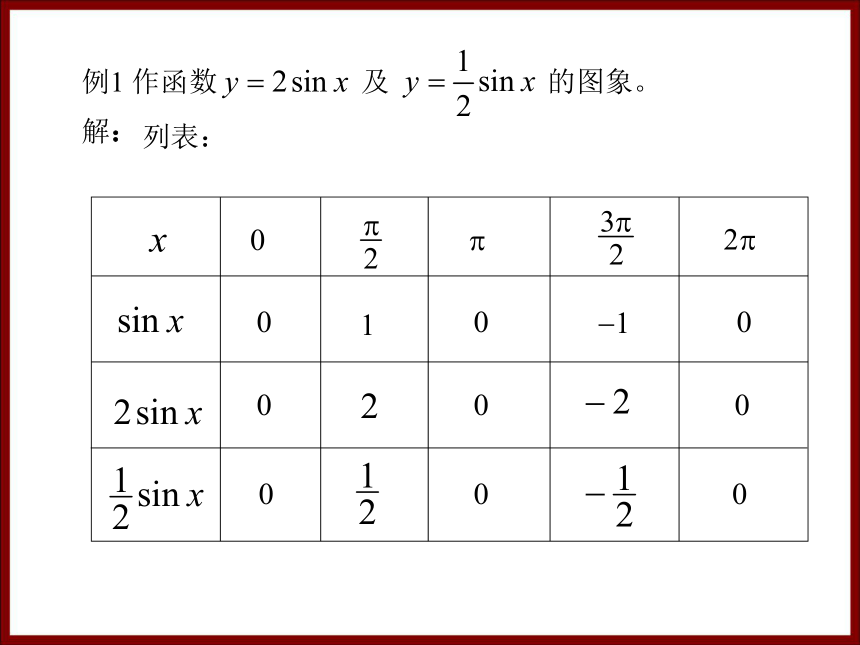
列表:
x
例1 作函数 及 的图象。
解:
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y= sinx
2. 描点、作图:
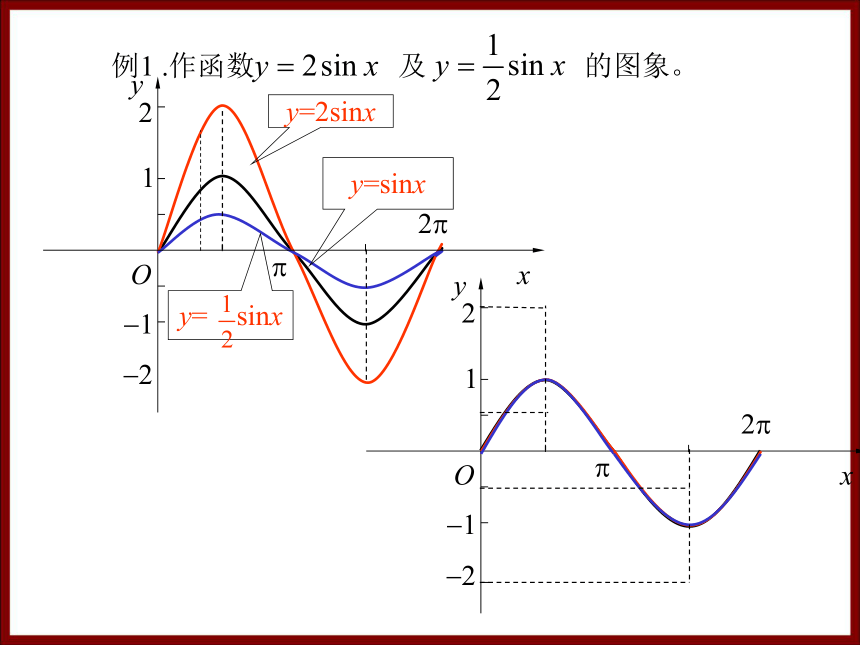
例1 .作函数 及 的图象。
x
y
O
2
1
2
2
1
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y= sinx
x
y
O
2
1
2
2
1
例1. 作函数 及 的图象。
x
y
O
2
1
2
2
1
y=2sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标伸长到原来的2倍。
y= sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标缩短到原来的 倍。
一、函数y=Asinx(A>0)的图象
函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0总结概括:函数y=Asinx(A>0)的图象
练习:作下列函数在长度为一个周期的闭区间上的简图:
1. 列表:
x
例2 .作函数 及 的图象。
x
O
y
2
1
2
2
1
3
2. 描点:
1. 列表:
x
y
O
2
1
1
3
4
2. 描点:
x
y
O
2
1
1
3
4
x
y
O
2
1
1
3
4
x
y
O
2
1
1
3
4
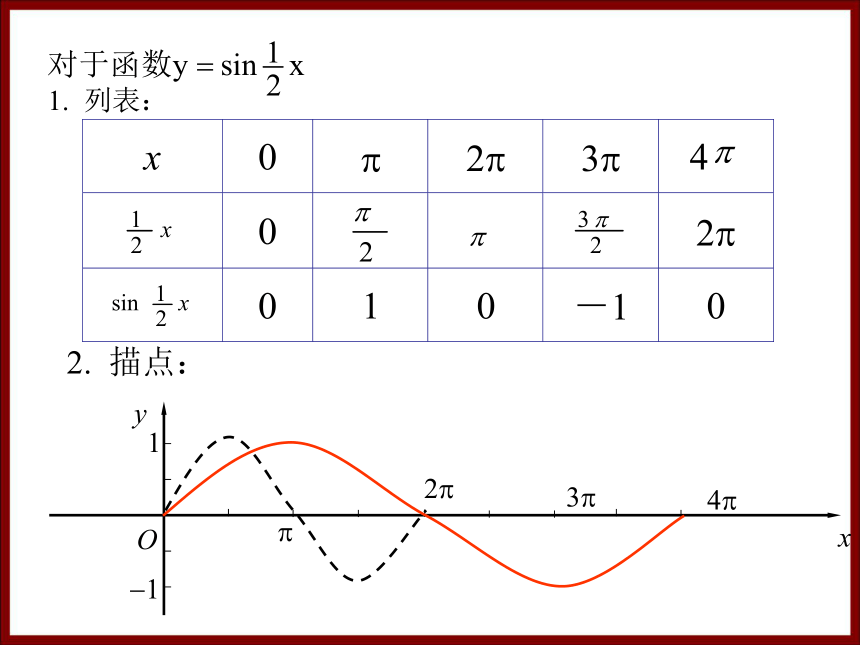
y=sin x的图象可以看作是把 y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)。
y=sin 2x的图象可以看作是把 y=sinx的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变)。
二、函数y=sin x( >0)图象
函数y=sin x ( >0且 ≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
练习:作下列函数在长度为一个周期的闭区间上的简图:
总结概括:函数y=sin x( >0)图象
x
O
2
1
1
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法一:
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法一:
x
y
O
2
1
1
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法二:
例3 .作函数 及 的图象。
x
0
1
0
-1
0
y
x
O
2
1
1
x
0
1
0
-1
0
x
O
2
1
1
x
O
2
1
1
三、函数y=sin(x+φ)图象
函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。
x
O
2
1
1
总结概括:函数y=sin(x+φ)图象
例4. 作函数 及 的图象。
x
0
1
0
-1
0
x
0
1
0
-1
0
y
x
O
1
1
y
x
O
1
1
y
x
O
1
1
例4 作函数 及 的图象。
四、函数y=sin(ωx+φ)与y=sinωx图象的关系
y
x
O
1
1
总结概括:函数y=sin(ωx+φ)与y=sinωx图象的关系
函数y=sin(ωx+φ) 的图象可以看作是把 y=sinωx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平
移| |个单位而得到的。
1、怎样由函数 的图象得到函数
的图象?
练习:
2、怎样由函数 的图象得到函数
的图象?
3、怎样由函数 的图象得到函数
的图象?
所有点的横坐标
伸长为原来的多少倍?
所有的点向那边
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
例5 .作函数 及 的图象。
x
O
2
1
1
函数y=sin( x +φ) ( >0且 ≠1)的图象可以看作是把 y=sin(x +φ) 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
所有点的横坐标
伸长为原来的2倍
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的2倍。
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
所有点的横坐标
伸长为原来的多少倍?
作y=sinx(长度为2 的某闭区间)
得y=sin(x+φ)
得y=sinωx
得y=sin(ωx+φ)
得y=sin(ωx+φ)
得y=Asin(ωx+φ)+B的图象,先在一个周期闭区间上再扩充到R上。
沿x轴平 移|φ|个单位
横坐标伸长或缩短
横坐标伸 长或缩短
沿x轴平 移| |个单位
纵坐标伸 长或缩短
纵坐标伸 长或缩短
小结:平移法过程(步骤)
两种方法殊途同归
作业:
1、P54习题1.8 A组2,3
2、预习三角函数的简单应用
作者:吕二动
单位:陕西省西安市高新区丈八五路39号 高新第三中学
邮编:710075
邮箱:lverdong@
QQ:251310042
§4.8y=Asin( x+ )+B
( 、A>0且≠1)的图象
北师大版数学必修四高一年级
列表:
x
例1 作函数 及 的图象。
解:
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y= sinx
2. 描点、作图:
例1 .作函数 及 的图象。
x
y
O
2
1
2
2
1
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y= sinx
x
y
O
2
1
2
2
1
例1. 作函数 及 的图象。
x
y
O
2
1
2
2
1
y=2sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标伸长到原来的2倍。
y= sinx的图象可以看作是把 y=sinx的图象上所有点的纵坐标缩短到原来的 倍。
一、函数y=Asinx(A>0)的图象
函数y=Asinx (A >0且A≠1)的图象可以看作是把 y=sinx 的图象上所有点的纵坐标伸长 (当A>1时)或缩短(当0
练习:作下列函数在长度为一个周期的闭区间上的简图:
1. 列表:
x
例2 .作函数 及 的图象。
x
O
y
2
1
2
2
1
3
2. 描点:
1. 列表:
x
y
O
2
1
1
3
4
2. 描点:
x
y
O
2
1
1
3
4
x
y
O
2
1
1
3
4
x
y
O
2
1
1
3
4
y=sin x的图象可以看作是把 y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)。
y=sin 2x的图象可以看作是把 y=sinx的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变)。
二、函数y=sin x( >0)图象
函数y=sin x ( >0且 ≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
练习:作下列函数在长度为一个周期的闭区间上的简图:
总结概括:函数y=sin x( >0)图象
x
O
2
1
1
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法一:
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法一:
x
y
O
2
1
1
3
4
伸长为原来的2倍
图象上各点横坐标
缩短为原来的一半
图象上各点纵坐标
法二:
例3 .作函数 及 的图象。
x
0
1
0
-1
0
y
x
O
2
1
1
x
0
1
0
-1
0
x
O
2
1
1
x
O
2
1
1
三、函数y=sin(x+φ)图象
函数y=sin(x+φ) 的图象可以看作是把 y=sinx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。
x
O
2
1
1
总结概括:函数y=sin(x+φ)图象
例4. 作函数 及 的图象。
x
0
1
0
-1
0
x
0
1
0
-1
0
y
x
O
1
1
y
x
O
1
1
y
x
O
1
1
例4 作函数 及 的图象。
四、函数y=sin(ωx+φ)与y=sinωx图象的关系
y
x
O
1
1
总结概括:函数y=sin(ωx+φ)与y=sinωx图象的关系
函数y=sin(ωx+φ) 的图象可以看作是把 y=sinωx 的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平
移| |个单位而得到的。
1、怎样由函数 的图象得到函数
的图象?
练习:
2、怎样由函数 的图象得到函数
的图象?
3、怎样由函数 的图象得到函数
的图象?
所有点的横坐标
伸长为原来的多少倍?
所有的点向那边
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
例5 .作函数 及 的图象。
x
O
2
1
1
函数y=sin( x +φ) ( >0且 ≠1)的图象可以看作是把 y=sin(x +φ) 的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时) 到原来的 倍(纵坐标不变) 而得到的。
所有点的横坐标
伸长为原来的2倍
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的2倍。
所有的点向右
平移多少个单位?
所有点的纵坐标
伸长为原来的多少倍?
所有点的横坐标
伸长为原来的多少倍?
作y=sinx(长度为2 的某闭区间)
得y=sin(x+φ)
得y=sinωx
得y=sin(ωx+φ)
得y=sin(ωx+φ)
得y=Asin(ωx+φ)+B的图象,先在一个周期闭区间上再扩充到R上。
沿x轴平 移|φ|个单位
横坐标伸长或缩短
横坐标伸 长或缩短
沿x轴平 移| |个单位
纵坐标伸 长或缩短
纵坐标伸 长或缩短
小结:平移法过程(步骤)
两种方法殊途同归
作业:
1、P54习题1.8 A组2,3
2、预习三角函数的简单应用
作者:吕二动
单位:陕西省西安市高新区丈八五路39号 高新第三中学
邮编:710075
邮箱:lverdong@
QQ:251310042
