8.5《抛物线及其标准方程》(旧人教版第二册上)
文档属性
| 名称 | 8.5《抛物线及其标准方程》(旧人教版第二册上) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-30 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
思考是一种寻觅。寻觅的过程充满混沌与艰辛,需穿越荒漠涉过险滩,有时则穿行在热闹的人群中,忍受着生活的单调和人们的误解。在失败时思考,是为了渡过人生的这一危机,在大声喧哗时思考,是为了保持冷静;在独处时思考,是为了更仔细地梳理命运的线索……思考的魅力是无穷的,善于思考是人生的一大财富。愿每位同学在学习生活中懂得思考,学会思考。
寄 语
课 前
8.5 抛物线及其标准方程
授课教师:秦安三中
成军昌
目标定位
新课讲授
课题导入
练习与小结
例题讲解
作业布置
首页
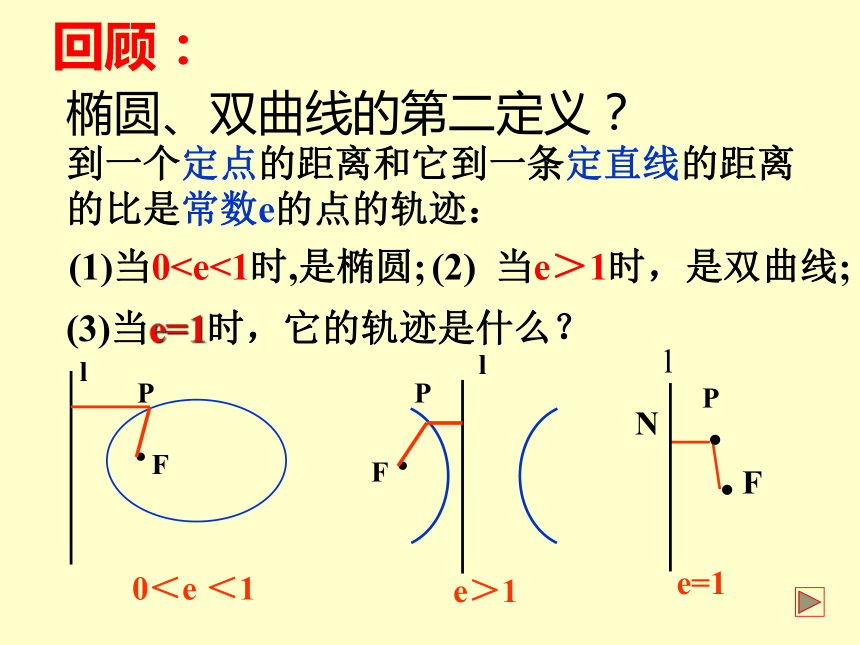
回顾:
椭圆、双曲线的第二定义?
到一个定点的距离和它到一条定直线的距离的比是常数e的点的轨迹:
·
P
F
l
0<e <1
l
F
·
P
e>1
(2) 当e>1时,是双曲线;
(3)当e=1时,它的轨迹是什么?
(1)当0·
F
N
e=1
·
P
l
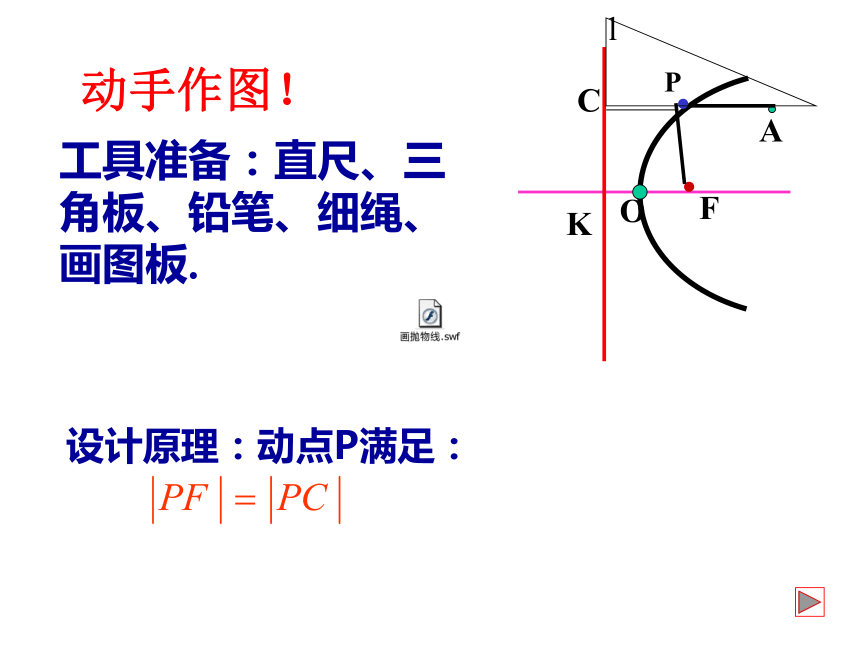
动手作图!
工具准备:直尺、三角板、铅笔、细绳、画图板.
设计原理:动点P满足:
K
O
A
·
·
F
P
l
C
问题1.求平面内到定点A(1,0)与定直线L:X=1距离相等的动点M的轨迹方程。
问题2.求平面内到定点A(1,0)与到定直线L:X=﹣1距离相等的动点M的轨迹方程。
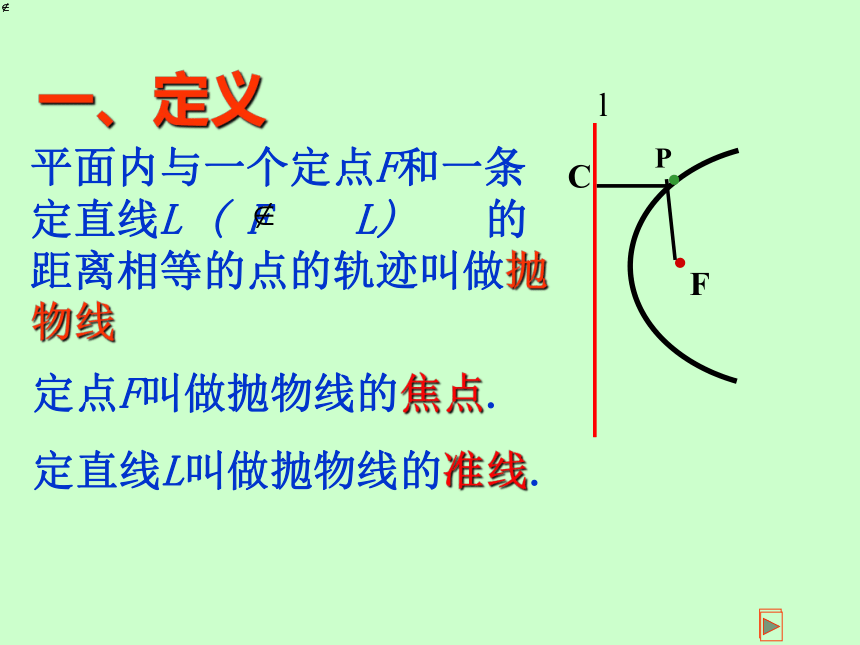
平面内与一个定点F和一条定直线L ( F L) 的距离相等的点的轨迹叫做抛物线
一、定义
定点F叫做抛物线的焦点.
定直线L叫做抛物线的准线.
·
·
F
P
l
C
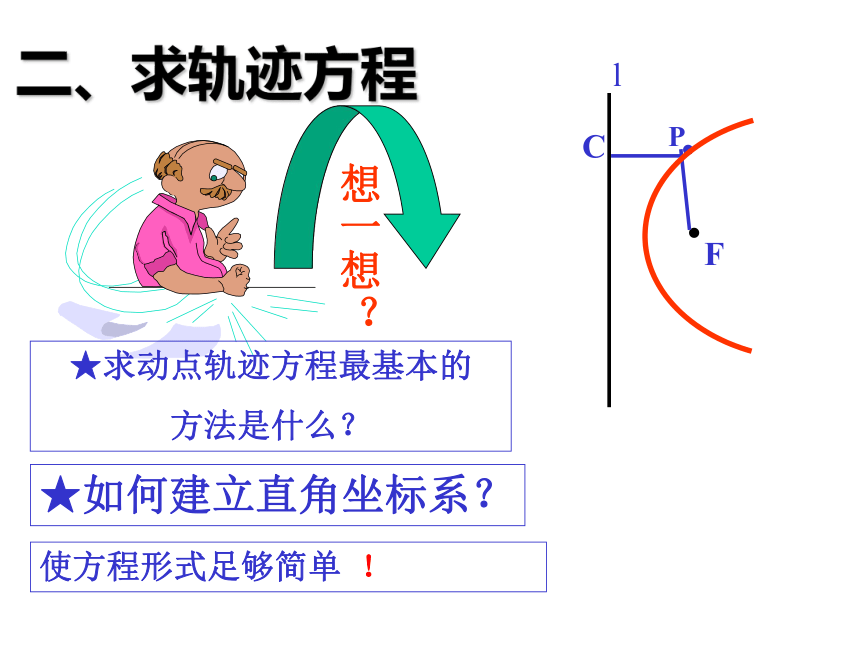
二、求轨迹方程
★如何建立直角坐标系?
想一想?
使方程形式足够简单 !
·
·
F
P
l
C
★求动点轨迹方程最基本的
方法是什么?
F
0
·
P
x
y
N
y=x2
·
·
F
P
l
C
建系技巧:
②对称轴为坐标轴(即焦点在坐标轴上).
①顶点在原点;
y
o
x
·
F
M
l
N
K
·
如图,已知定点F及定直线L,动点M满足:到定点F (F L) 的距离与到定直线L的距离相等,求动点M的轨迹方程.
解:如图,建立直角坐标系,使X轴经过点F且垂直于直线L,垂足为K,并使原点与线段KF的中点重合。
设︱KF︱= p(p>0)
则F( ,0), L :x = -
p
2
p
2
设点M的坐标为(x,y),
由定义可知,
2
化简得 y2 = 2px(p>0)
方程 y2 = 2px(p>0)叫做抛物线的标准方程.
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
结论:
此方程表示的是开口向右,焦点
在 x轴的正半轴上的抛物线.
且焦点坐标为
准线方程为
y
o
x
·
F
M
l
N
K
·
一般地,由于它在平面内的位置不同,方程也不同,也就是说由于焦点的位置不同,导致抛物线的标准方程还有以下几种形式,总结如下:
图 形 焦 点 准 线 标准方程
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
◆对于给定的抛物线标准方程,如何判断抛物线的焦点位置,开口方向?
想一想:
第一:一次项的变量如为x(或y), 则x轴(或y轴)为抛物线的对称轴,焦点就在对称轴上!
第二:一次项的系数的正负决定了开口方向.
例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程。
解:因焦点在y轴的负半轴上,则抛物线的标准方程为
x 2 = -2py ,易知p=4,故其标准方程为:x 2 = -8y。
解:由y2 = 6x可知对应的抛物经开口向右,又因为p=3,故焦点坐标为 ,准线方程为
解:标准方程为: , 故 是开口向下的抛物线。 ,焦点坐标为 , 准线方程为
首页
例2、求过点A(-3,2)的抛物线的标准方程。
.
A
O
y
x
①当抛物线的焦点在y轴的正半轴上时,可设方程为x2 =2py,
得p=
解:由A点在第二象限知,抛物线只可能为
开口向上、向左两种类型.
∴抛物线的标准方程为
(1)焦点在y轴正半轴上时
(2)当焦点在x轴的负半轴上时
代入A(-3,2)
可得 p=
②当焦点在x轴的负半轴上时,
可设方程为y2 = -2px,
代入A(-3,2)
练习:
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2准线方程 是x = ;
(3)焦点到准线的距离是2.
y2 =12x
y2 =x
y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y
2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
小 结 :
1、关于抛物线的定义,要注意点F不在直线L上,否则轨迹是一条直线。
2、关于抛物线的标准方程,在求抛物线的标准方程时,以抛物线的顶点为原点,对称轴为一条坐标轴建立坐标系,这样使标准方程不仅具有对称性,而且曲线过原点,形式更为简单,便于应用。
抛物线的标准方程有四种不同的形式,其联系与区别在于:
(1)焦参数p的几何意义都是焦点到准线的距离;
(2)方程右边一次项的变量与焦点所在的坐标轴(对称轴)名称相 同,一次项系数的正负决定抛物线的开口方向。
(3)焦点的非零坐标是一次项系数的1/4。
3、注重数形结合和分类讨论的思想。做题时注重以形助数!
温馨提醒
学数学知识应努力做到学规律、学本质、学思想方法,并通过例题逐步加深对所学知识的理解和掌握,直至达到灵活应用的目的,一般地,学习数学知识有以下三个过程:
一,对所学知识进行加工处理,使之条理化、系统化,形成完整的知识体系,并按照一定的规律形式化,便于存贮记忆;
二,通过知识的内在联系,体会其中蕴含的数学思想方法,这是数学的灵魂;
三,要注意对知识本质的认识和理解,并通过运用知识解决实际问题的过程是不断深化对知识本质的认识。
做到以上三点,你就站在一定高度了,有居高临下之感。有道是:会当凌绝顶,一览众山小。
课后作业:
1.习题8.5第1,2,3,4题 ;
2.探究抛物线焦点弦的有关几何性质。
祝你成功!
思考是一种寻觅。寻觅的过程充满混沌与艰辛,需穿越荒漠涉过险滩,有时则穿行在热闹的人群中,忍受着生活的单调和人们的误解。在失败时思考,是为了渡过人生的这一危机,在大声喧哗时思考,是为了保持冷静;在独处时思考,是为了更仔细地梳理命运的线索……思考的魅力是无穷的,善于思考是人生的一大财富。愿每位同学在学习生活中懂得思考,学会思考。
寄 语
课 前
8.5 抛物线及其标准方程
授课教师:秦安三中
成军昌
目标定位
新课讲授
课题导入
练习与小结
例题讲解
作业布置
首页
回顾:
椭圆、双曲线的第二定义?
到一个定点的距离和它到一条定直线的距离的比是常数e的点的轨迹:
·
P
F
l
0<e <1
l
F
·
P
e>1
(2) 当e>1时,是双曲线;
(3)当e=1时,它的轨迹是什么?
(1)当0
F
N
e=1
·
P
l
动手作图!
工具准备:直尺、三角板、铅笔、细绳、画图板.
设计原理:动点P满足:
K
O
A
·
·
F
P
l
C
问题1.求平面内到定点A(1,0)与定直线L:X=1距离相等的动点M的轨迹方程。
问题2.求平面内到定点A(1,0)与到定直线L:X=﹣1距离相等的动点M的轨迹方程。
平面内与一个定点F和一条定直线L ( F L) 的距离相等的点的轨迹叫做抛物线
一、定义
定点F叫做抛物线的焦点.
定直线L叫做抛物线的准线.
·
·
F
P
l
C
二、求轨迹方程
★如何建立直角坐标系?
想一想?
使方程形式足够简单 !
·
·
F
P
l
C
★求动点轨迹方程最基本的
方法是什么?
F
0
·
P
x
y
N
y=x2
·
·
F
P
l
C
建系技巧:
②对称轴为坐标轴(即焦点在坐标轴上).
①顶点在原点;
y
o
x
·
F
M
l
N
K
·
如图,已知定点F及定直线L,动点M满足:到定点F (F L) 的距离与到定直线L的距离相等,求动点M的轨迹方程.
解:如图,建立直角坐标系,使X轴经过点F且垂直于直线L,垂足为K,并使原点与线段KF的中点重合。
设︱KF︱= p(p>0)
则F( ,0), L :x = -
p
2
p
2
设点M的坐标为(x,y),
由定义可知,
2
化简得 y2 = 2px(p>0)
方程 y2 = 2px(p>0)叫做抛物线的标准方程.
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
结论:
此方程表示的是开口向右,焦点
在 x轴的正半轴上的抛物线.
且焦点坐标为
准线方程为
y
o
x
·
F
M
l
N
K
·
一般地,由于它在平面内的位置不同,方程也不同,也就是说由于焦点的位置不同,导致抛物线的标准方程还有以下几种形式,总结如下:
图 形 焦 点 准 线 标准方程
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
◆对于给定的抛物线标准方程,如何判断抛物线的焦点位置,开口方向?
想一想:
第一:一次项的变量如为x(或y), 则x轴(或y轴)为抛物线的对称轴,焦点就在对称轴上!
第二:一次项的系数的正负决定了开口方向.
例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程。
解:因焦点在y轴的负半轴上,则抛物线的标准方程为
x 2 = -2py ,易知p=4,故其标准方程为:x 2 = -8y。
解:由y2 = 6x可知对应的抛物经开口向右,又因为p=3,故焦点坐标为 ,准线方程为
解:标准方程为: , 故 是开口向下的抛物线。 ,焦点坐标为 , 准线方程为
首页
例2、求过点A(-3,2)的抛物线的标准方程。
.
A
O
y
x
①当抛物线的焦点在y轴的正半轴上时,可设方程为x2 =2py,
得p=
解:由A点在第二象限知,抛物线只可能为
开口向上、向左两种类型.
∴抛物线的标准方程为
(1)焦点在y轴正半轴上时
(2)当焦点在x轴的负半轴上时
代入A(-3,2)
可得 p=
②当焦点在x轴的负半轴上时,
可设方程为y2 = -2px,
代入A(-3,2)
练习:
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2准线方程 是x = ;
(3)焦点到准线的距离是2.
y2 =12x
y2 =x
y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y
2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
小 结 :
1、关于抛物线的定义,要注意点F不在直线L上,否则轨迹是一条直线。
2、关于抛物线的标准方程,在求抛物线的标准方程时,以抛物线的顶点为原点,对称轴为一条坐标轴建立坐标系,这样使标准方程不仅具有对称性,而且曲线过原点,形式更为简单,便于应用。
抛物线的标准方程有四种不同的形式,其联系与区别在于:
(1)焦参数p的几何意义都是焦点到准线的距离;
(2)方程右边一次项的变量与焦点所在的坐标轴(对称轴)名称相 同,一次项系数的正负决定抛物线的开口方向。
(3)焦点的非零坐标是一次项系数的1/4。
3、注重数形结合和分类讨论的思想。做题时注重以形助数!
温馨提醒
学数学知识应努力做到学规律、学本质、学思想方法,并通过例题逐步加深对所学知识的理解和掌握,直至达到灵活应用的目的,一般地,学习数学知识有以下三个过程:
一,对所学知识进行加工处理,使之条理化、系统化,形成完整的知识体系,并按照一定的规律形式化,便于存贮记忆;
二,通过知识的内在联系,体会其中蕴含的数学思想方法,这是数学的灵魂;
三,要注意对知识本质的认识和理解,并通过运用知识解决实际问题的过程是不断深化对知识本质的认识。
做到以上三点,你就站在一定高度了,有居高临下之感。有道是:会当凌绝顶,一览众山小。
课后作业:
1.习题8.5第1,2,3,4题 ;
2.探究抛物线焦点弦的有关几何性质。
祝你成功!
同课章节目录
