冀教版数学九年级上册 23.1平均数(1)课件(26张PPT)
文档属性
| 名称 | 冀教版数学九年级上册 23.1平均数(1)课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 983.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 20:28:53 | ||
图片预览







文档简介
(共26张PPT)
复习回顾
1、数据收集与整理的一般步骤是什么?
1)确定调查对象
2)确定调查方法(普查和抽样调查)
3)收集数据
4)整理数据(统计表格或统计图)
5)得出结论
2、统计图包括哪些?
3、总体、个体、样本、样本容量的含意是什么?
23.1平均数(1)
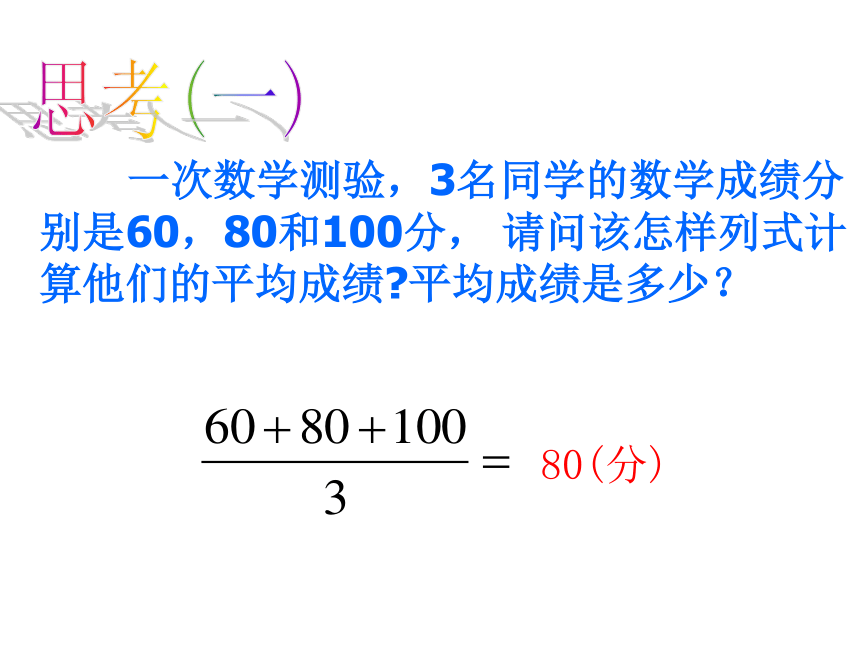
一次数学测验,3名同学的数学成绩分别是60,80和100分,
请问该怎样列式计算他们的平均成绩?平均成绩是多少?
80(分)
如果有n个数(用χ1、χ2、χ3、…χn表示),那么它们的平均数我们表示为
一般地:
注意:
通过这种计算方法得到的平均数叫做这n个数的算数平均数
如果知道有一个小组中3名学生得了60分,5名学生得了80分,还有一名学生得了100分,此时这个小组的数学测验平均分还是思考(一)中的答案吗?该如何计算呢?
≈75.6
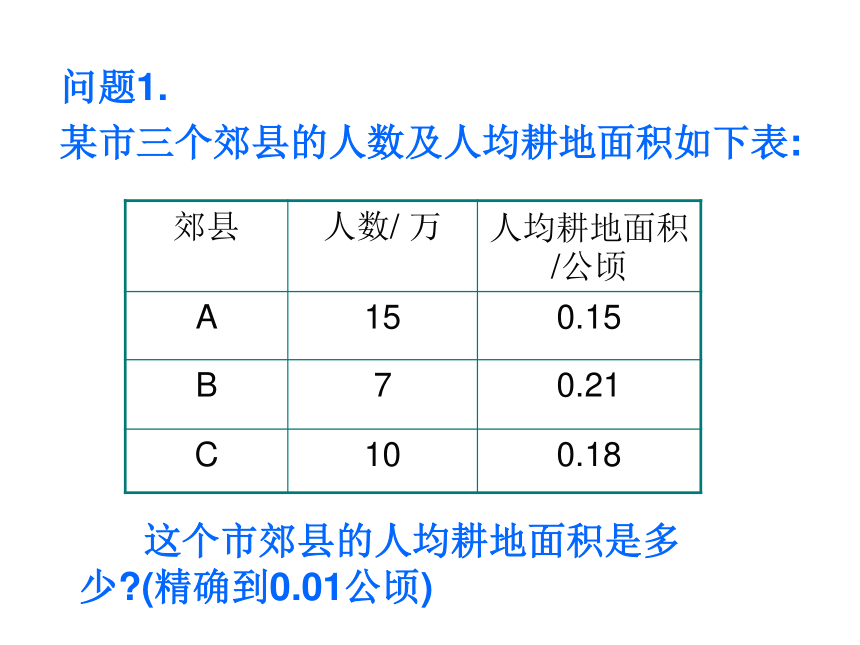
问题1.
某市三个郊县的人数及人均耕地面积如下表:
郊县
人数/
万
人均耕地面积/公顷
A
15
0.15
B
7
0.21
C
10
0.18
这个市郊县的人均耕地面积是多少?(精确到0.01公顷)
郊县
人数(万)
人均耕地面积(公顷)
A
15
0.15
B
7
0.21
C
10
0.18
≈0.17
(公颂).
讨论
小明求得这个市郊县的人均耕地面积为
你认为小明的做法有道理吗?为什么?
=0.18
(公颂).
某校规定学生的体育成绩由三部分组成:平时早锻炼及体育课外活动占成绩的20%,体育半期测试占30%,体育期末测试占50%。小颖的上述三项成绩依次为92分、80分、84分,则小颖这学期体育的综合评定成绩是多少?
问题2:
解:
小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4分
答:小颖这学期的体育成绩是84.4分。
≈0.17(公顷)
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。所以,在计算这组数据的平均数时,往往给每个数据一个“权
”。
如问题1中的15就是0.15的权、7是0.21的权、10是0.18的权。
而称
为0.15,0.21,0.18的
加权平均数
。
92×20%+80×30%+84×50%=84.4
(分)
再看看问题2
某校规定学生的体育成绩由三部分组成:平时早锻炼及体育课外活动占成绩的20%,体育半期测试占30%,体育期末测试占50%。小颖的上述三项成绩依次为92分、80分、84分,则小颖这学期体育的综合评定成绩是多少?
分析:由题意可知,平时:半期:期末=2:3:5
解:
小颖这学期的体育成绩是
84.4
即:
92×20%+80×30%+84×50%=84.4
(分)
≈0.17(公顷)
对比一下
注意:1)〝权〞表示了数据的重要程度
2)〝权〞常表示数据出现的次数或
数据所占的百分比
一般地:
2)如果这家公司想招一名口语能力较强的翻译,听说读写成绩按3:3:2:2
的比确定,应该录取谁?
例1
一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英文水平测试.他们的各项成绩(百分制)如下:
3)如果这家公司想招一名笔译能力较强的翻译,听说读写成绩按2:2:3:3的比确定,应该录取谁?
1)如果直接比较两人的平均成绩,应该录取谁?
解:(2)听说读写的成绩按3:3:2:2
的比确定,则甲的平均成绩为
乙的平均成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲。
=81
=79.3
(3)听说读写的成绩按2:2:3:3的比确定,则
甲的平均成绩为
乙的平均成绩为
显然乙的成绩比甲高,所以从成绩看,应该录取乙。
=79.5
=80.7
例2
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
解:选手A的最后得分是
=42.5+38+9.5
=90
选手B的最后得分是
=47.5+34+9.5
=91
由上可知选手B获得第一名,选手A获得第二名
请决出两人的名次?
练习
某公司欲招聘公关人员,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取
候选人
测试成绩(百分制)
面试
笔试
甲
86
90
乙
92
83
解:
∵
∴
(2)如果公司认为,作为公关人员面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
练习
某公司欲招聘公关人员,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示
候选人
测试成绩(百分制)
测试
笔试
甲
86
90
乙
92
83
解:
∵
∴
巩固练习
1、某班10名学生为支援希望工程,将平时积攒的零花钱捐献给贫困地区的失学儿童。每人捐款金额如下(单位:元):
10,
12,
13.5,
21,
40.8,
19.5,
20.8,
25,
16,
30。
这10名同学平均捐款多少元?
解:这10名同学平均捐款为
(10+12+13.5+21+40.8+19.5+20.8+25+16+30)
=
20.86元
答:这10名同学平均捐款20.86元。
2、八年级一班有学生50人,二班有45人。期末数学测试成绩中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解: (50×81.5+45×83.4)=82.4(分)
答:两个班95名学生的平均分是82.4分。
注意:
延伸与提高
1、选择
(1)某次考试,5名学生的平均分是82,除甲外,其余4名
学生的平均分是80,那么甲的得分是
(A)84
(B)
86
(C)
88
(D)
90
(
D
)
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2
B:(x+y)/(m+n)
C:(mx+ny)/(x+y)
D:(mx+ny)/(m+n)
(
D
)
3、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1
的平均数是
(A)
a
(B)2a
(C)
2a+1
(D)
2a/3+1
解(1):由题意可得(1+2+3+x+y+z)/6=4
即
1+2+3+x+y+z=24
所以
x+y+z=18
所以
(x+y+z)/3=18/3=6
(
C
)
思考题:
一组6个数1,2,3,x,
y,
z
的平均数是
4
(1)求x,
y,
z
三数的平均数;
(2)求
4x+5,
4y+6,
4z+7
的平均数。
解(2):
由上题知
x+y+z=18
∴(
4x+5)+(4y+6)+(4z+7)
=4(x+y+z)+18
=4×18+18
=
90
∴(4x+5+4y+6+4z+7)/3
=
90/3
=
30
思考题:
一组6个数1,2,3,x,
y,
z
的平均数是
4
(1)求x,
y,
z
三数的平均数;
(2)求
4x+5,
4y+6,
4z+7
的平均数。
如果有n个数(用χ1、χ2、χ3、…χn表示),那么它们的平均数我们表示为
一般地:
注意:
通过这种计算方法得到的平均数叫做这n个数的算数平均数
小结
注意:1)〝权〞表示了数据的重要程度
2)〝权〞常表示数据出现的次数或
百分比
一般地:
再见
数据的收集
数据的整理
数据的描述
数据的分析
复习回顾
1、数据收集与整理的一般步骤是什么?
1)确定调查对象
2)确定调查方法(普查和抽样调查)
3)收集数据
4)整理数据(统计表格或统计图)
5)得出结论
2、统计图包括哪些?
3、总体、个体、样本、样本容量的含意是什么?
23.1平均数(1)
一次数学测验,3名同学的数学成绩分别是60,80和100分,
请问该怎样列式计算他们的平均成绩?平均成绩是多少?
80(分)
如果有n个数(用χ1、χ2、χ3、…χn表示),那么它们的平均数我们表示为
一般地:
注意:
通过这种计算方法得到的平均数叫做这n个数的算数平均数
如果知道有一个小组中3名学生得了60分,5名学生得了80分,还有一名学生得了100分,此时这个小组的数学测验平均分还是思考(一)中的答案吗?该如何计算呢?
≈75.6
问题1.
某市三个郊县的人数及人均耕地面积如下表:
郊县
人数/
万
人均耕地面积/公顷
A
15
0.15
B
7
0.21
C
10
0.18
这个市郊县的人均耕地面积是多少?(精确到0.01公顷)
郊县
人数(万)
人均耕地面积(公顷)
A
15
0.15
B
7
0.21
C
10
0.18
≈0.17
(公颂).
讨论
小明求得这个市郊县的人均耕地面积为
你认为小明的做法有道理吗?为什么?
=0.18
(公颂).
某校规定学生的体育成绩由三部分组成:平时早锻炼及体育课外活动占成绩的20%,体育半期测试占30%,体育期末测试占50%。小颖的上述三项成绩依次为92分、80分、84分,则小颖这学期体育的综合评定成绩是多少?
问题2:
解:
小颖这学期的体育成绩是
92×20%+80×30%+84×50%=84.4分
答:小颖这学期的体育成绩是84.4分。
≈0.17(公顷)
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。所以,在计算这组数据的平均数时,往往给每个数据一个“权
”。
如问题1中的15就是0.15的权、7是0.21的权、10是0.18的权。
而称
为0.15,0.21,0.18的
加权平均数
。
92×20%+80×30%+84×50%=84.4
(分)
再看看问题2
某校规定学生的体育成绩由三部分组成:平时早锻炼及体育课外活动占成绩的20%,体育半期测试占30%,体育期末测试占50%。小颖的上述三项成绩依次为92分、80分、84分,则小颖这学期体育的综合评定成绩是多少?
分析:由题意可知,平时:半期:期末=2:3:5
解:
小颖这学期的体育成绩是
84.4
即:
92×20%+80×30%+84×50%=84.4
(分)
≈0.17(公顷)
对比一下
注意:1)〝权〞表示了数据的重要程度
2)〝权〞常表示数据出现的次数或
数据所占的百分比
一般地:
2)如果这家公司想招一名口语能力较强的翻译,听说读写成绩按3:3:2:2
的比确定,应该录取谁?
例1
一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英文水平测试.他们的各项成绩(百分制)如下:
3)如果这家公司想招一名笔译能力较强的翻译,听说读写成绩按2:2:3:3的比确定,应该录取谁?
1)如果直接比较两人的平均成绩,应该录取谁?
解:(2)听说读写的成绩按3:3:2:2
的比确定,则甲的平均成绩为
乙的平均成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲。
=81
=79.3
(3)听说读写的成绩按2:2:3:3的比确定,则
甲的平均成绩为
乙的平均成绩为
显然乙的成绩比甲高,所以从成绩看,应该录取乙。
=79.5
=80.7
例2
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
解:选手A的最后得分是
=42.5+38+9.5
=90
选手B的最后得分是
=47.5+34+9.5
=91
由上可知选手B获得第一名,选手A获得第二名
请决出两人的名次?
练习
某公司欲招聘公关人员,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取
候选人
测试成绩(百分制)
面试
笔试
甲
86
90
乙
92
83
解:
∵
∴
(2)如果公司认为,作为公关人员面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
练习
某公司欲招聘公关人员,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示
候选人
测试成绩(百分制)
测试
笔试
甲
86
90
乙
92
83
解:
∵
∴
巩固练习
1、某班10名学生为支援希望工程,将平时积攒的零花钱捐献给贫困地区的失学儿童。每人捐款金额如下(单位:元):
10,
12,
13.5,
21,
40.8,
19.5,
20.8,
25,
16,
30。
这10名同学平均捐款多少元?
解:这10名同学平均捐款为
(10+12+13.5+21+40.8+19.5+20.8+25+16+30)
=
20.86元
答:这10名同学平均捐款20.86元。
2、八年级一班有学生50人,二班有45人。期末数学测试成绩中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解: (50×81.5+45×83.4)=82.4(分)
答:两个班95名学生的平均分是82.4分。
注意:
延伸与提高
1、选择
(1)某次考试,5名学生的平均分是82,除甲外,其余4名
学生的平均分是80,那么甲的得分是
(A)84
(B)
86
(C)
88
(D)
90
(
D
)
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2
B:(x+y)/(m+n)
C:(mx+ny)/(x+y)
D:(mx+ny)/(m+n)
(
D
)
3、已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1
的平均数是
(A)
a
(B)2a
(C)
2a+1
(D)
2a/3+1
解(1):由题意可得(1+2+3+x+y+z)/6=4
即
1+2+3+x+y+z=24
所以
x+y+z=18
所以
(x+y+z)/3=18/3=6
(
C
)
思考题:
一组6个数1,2,3,x,
y,
z
的平均数是
4
(1)求x,
y,
z
三数的平均数;
(2)求
4x+5,
4y+6,
4z+7
的平均数。
解(2):
由上题知
x+y+z=18
∴(
4x+5)+(4y+6)+(4z+7)
=4(x+y+z)+18
=4×18+18
=
90
∴(4x+5+4y+6+4z+7)/3
=
90/3
=
30
思考题:
一组6个数1,2,3,x,
y,
z
的平均数是
4
(1)求x,
y,
z
三数的平均数;
(2)求
4x+5,
4y+6,
4z+7
的平均数。
如果有n个数(用χ1、χ2、χ3、…χn表示),那么它们的平均数我们表示为
一般地:
注意:
通过这种计算方法得到的平均数叫做这n个数的算数平均数
小结
注意:1)〝权〞表示了数据的重要程度
2)〝权〞常表示数据出现的次数或
百分比
一般地:
再见
数据的收集
数据的整理
数据的描述
数据的分析
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
