冀教版数学九年级上册23.1加权平均数 课件 (27张PPT)
文档属性
| 名称 | 冀教版数学九年级上册23.1加权平均数 课件 (27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
23.1加权平均数
活动一:教学引入
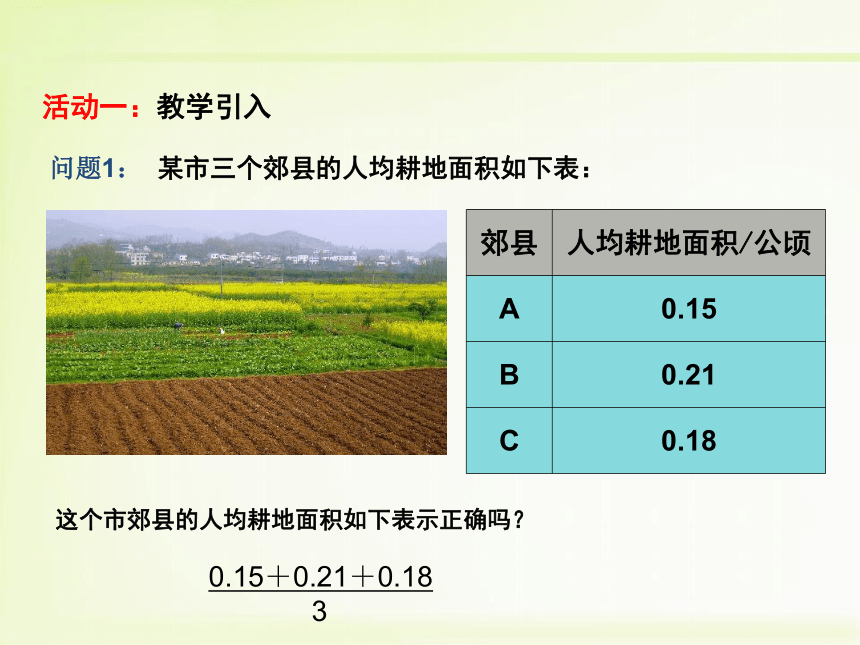
问题1:
某市三个郊县的人均耕地面积如下表:
郊县
人均耕地面积/公顷
A
0.15
B
0.21
C
0.18
这个市郊县的人均耕地面积如下表示正确吗?
0.15+0.21+0.18
3
活动二:引例归纳
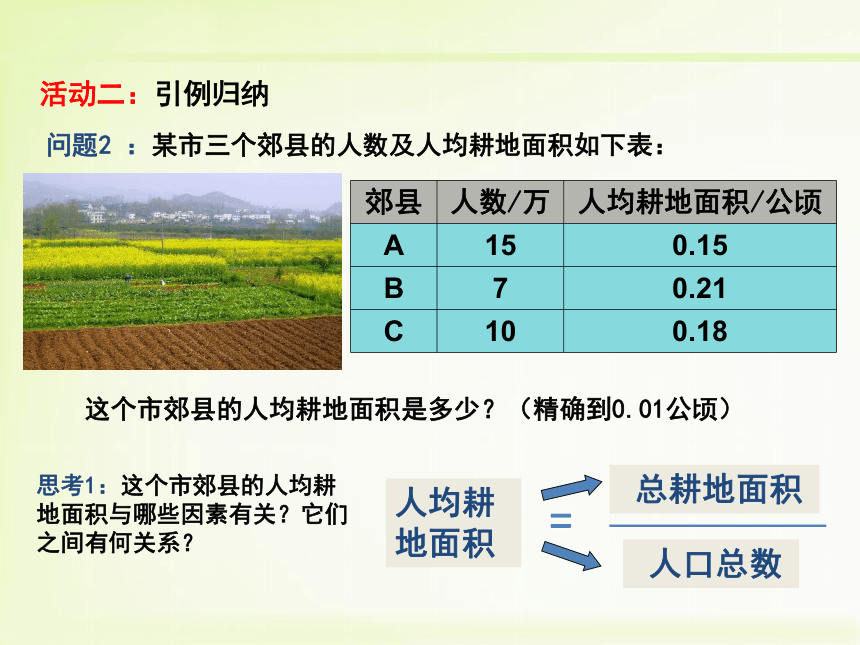
思考1:这个市郊县的人均耕地面积与哪些因素有关?它们之间有何关系?
人均耕地面积
总耕地面积
问题2
:某市三个郊县的人数及人均耕地面积如下表:
郊县
人数/万
人均耕地面积/公顷
A
15
0.15
B
7
0.21
C
10
0.18
人口总数
=
这个市郊县的人均耕地面积是多少?(精确到0.01公顷)
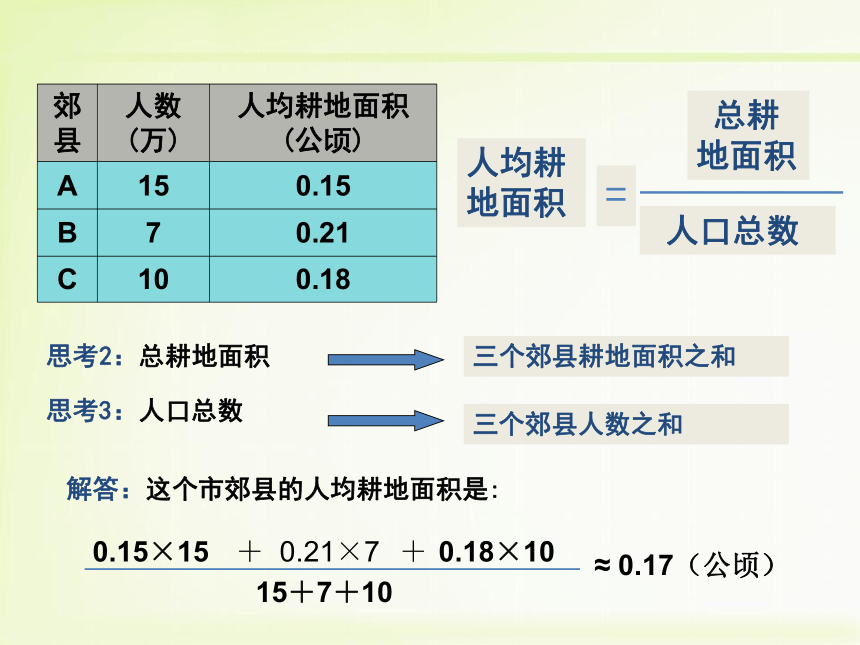
0.15×15
0.21×7
0.18×10
+
+
15+7+10
≈
0.17(公顷)
解答:这个市郊县的人均耕地面积是:
郊县
人数(万)
人均耕地面积(公顷)
A
15
0.15
B
7
0.21
C
10
0.18
思考2:总耕地面积
三个郊县耕地面积之和
思考3:人口总数
三个郊县人数之和
人均耕地面积
=
总耕地面积
人口总数
我们就把上面求得的平均数0.17称为三个数0.15、0.21、0.18的
加权平均数,由于各郊县的人数不同,各郊县的人均耕地面积对这个市郊县的人均耕地面积的影响就不同.因此我们把三个郊县的人数(单位:万)15、7、10分别称为三个数据的权.
“权”的英文是
Weight,有表示数据重要程度的意思.即数据的权能反映数据的相对“重要程度”.
特别提示
这很重要,好好理解哟
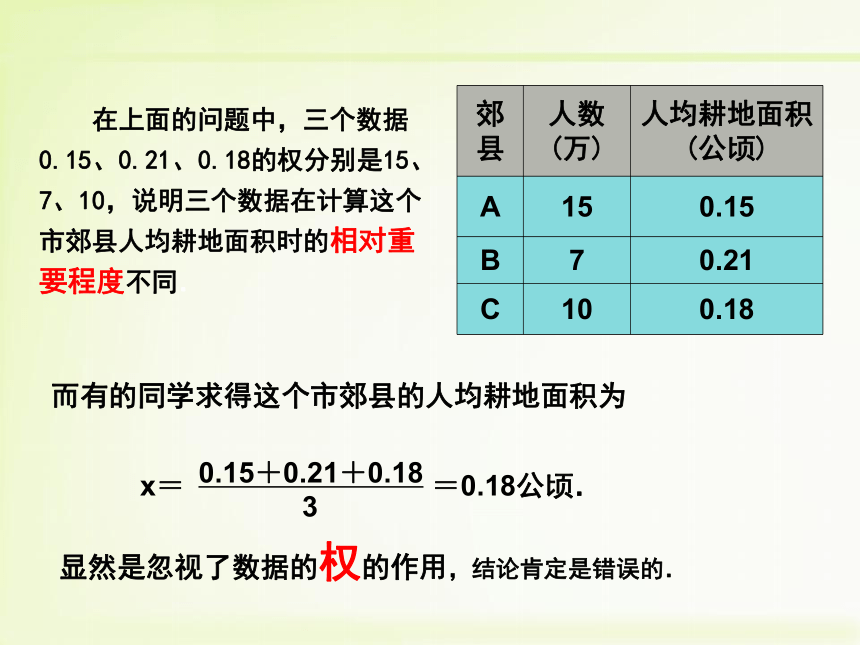
而有的同学求得这个市郊县的人均耕地面积为
x=
0.15+0.21+0.18
3
=0.18公顷.
显然是忽视了数据的权的作用,结论肯定是错误的.
郊县
人数(万)
人均耕地面积(公顷)
A
15
0.15
B
7
0.21
C
10
0.18
在上面的问题中,三个数据0.15、0.21、0.18的权分别是15、7、10,说明三个数据在计算这个市郊县人均耕地面积时的相对重要程度不同.
郊县
人数(万)
人均耕地面积(公顷)
A
B
C
x
1
x
2
x
3
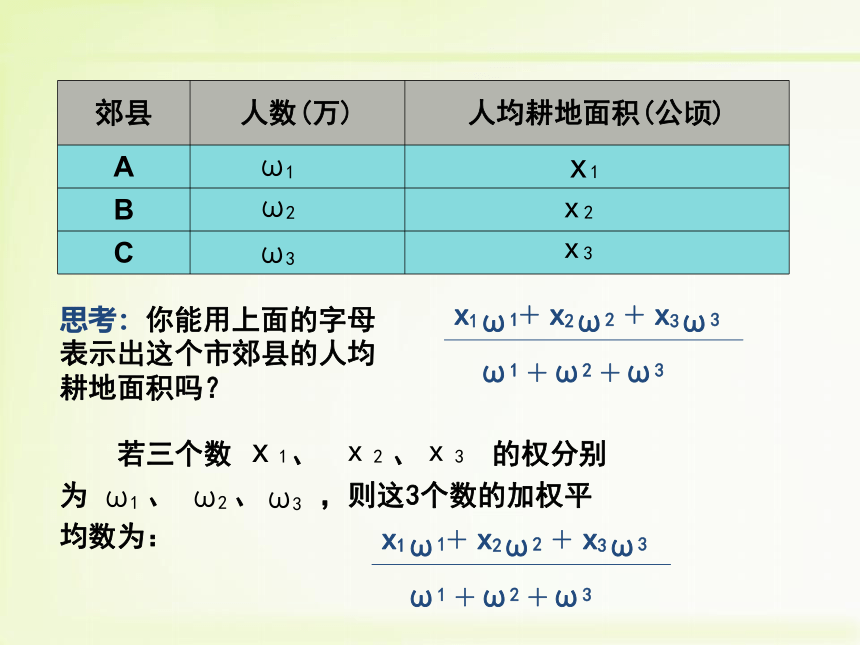
思考:你能用上面的字母表示出这个市郊县的人均耕地面积吗?
ω
1
ω
2
ω
3
若三个数
、
、
的权分别为
、
、
,则这3个数的加权平均数为:
ω
1
x
2
x
1
x
3
ω
2
ω
3
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
ω
3
ω
2
ω
1
+
+
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
ω
3
ω
2
ω
1
+
+
若n个数
、
、
、…
、
的权分别为
、
、
、…
、
则这n个数的加权平均数为:
ω
n
x
n
ω
3
ω
1
ω
2
x
2
x
1
x
3
活动三:课堂举例
例1
一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
思考(1)这家公司在招聘英文翻译时,对甲乙两名应试者进行了哪几方面的英语水平测试?成绩分别是多少?
思考(2)招口语能力较强的翻译,“听、说、读、写成绩按照3∶3∶2∶2的比确定”,说明公司侧重于哪几个方面的成绩?
思考(3)计算两名候选人的平均成绩实际上就是求两人听、说、读、写四项成绩的加权平均数,那么它们的权分别是什么?
认真思考,你一定行的.
解:(1)听、说、读、写的成绩按照3∶3∶2∶2的比确定,则甲的平均成绩为
85×3+83×3+78×2+75×2
3+3+2+2
=
81
乙的平均成绩为
73×3+80×3+85×2+82×2
3+3+2+2
=
79.3.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
仔细看,要记住正确的书写格式哟
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2∶2∶3∶3的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
思考(1)招笔译能力较强的翻译,“听、说、读、写成绩按照2∶2∶3∶3的比确定”,说明公司侧重于哪几个方面的成绩?
思考(2)计算两名候选人的平均成绩实际上就是求两人听、说、读、写四项成绩的加权平均数,那么它们的权分别是什么?
解:(2)听、说、读、写的成绩按照2∶2∶3∶3的比确定,则甲的平均成绩为
85×2+83×2+78×3+75×3
2+2+3+3
=
79.5
乙的平均成绩为
73×2+80×2+85×3+82×3
2+2+3+3
=
80.7
显然乙的成绩比甲的高,所以从成绩看,应该录取乙.
你掌握正确的书写格式了吗?
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
例2
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
思考(1)你认为在计算选手的综合成绩时侧重于哪个方面的成绩?三项成绩的权分别是多少?
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考(2)利用加权平均数公式你能求出甲、乙的综合成绩,决出两人的名次吗?
认真思考,一定能回答正确的。
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考两名选手的单项成绩都是两个95分与一个85分,为什么他们的最后得分不同?从中你能体会到权的作用吗?
选手A的95分是演讲能力,B的95分是演讲内容,而根据题意可知,演讲内容所占的权重比演讲能力所占的权重大,所以A的95分就不如B的95分在综合成绩中占的分值大.在此更能显示出“权”的重要性.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
你真正理解了吗?
活动四:当堂练习
1、某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如下表所示:
候选人
测试成绩(百分制)
面试
笔试
甲
86
90
乙
92
83
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁将被录取?
解:(1)面试和笔试同等重
要时,甲的平均成绩为
86×5+90×5
5+5
=43+45
=88.
乙的平均成绩为
92×5+83×5
5+5
=46+41.5
=87.5.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
候选人
测试成绩
(百分制)
面试
笔试
甲
86
90
乙
92
83
对比一下,你写的解题过程合理吗?
(2)面试和笔试分别赋予它们6和4的权,则甲的平均成绩为
86×6+90×4
6+4
=51.6+36
=87.6.
乙的平均成绩为
92×6+83×4
6+4
=55.2+33.2
=88.4.
显然乙的成绩比甲的高,所以从成绩看,应该录取乙.
候选人
测试成绩
(百分制)
面试
笔试
甲
86
90
乙
92
83
这次你的书写过程怎么样呢?
2、晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95分、90分、85分,小桐这学期的体育成绩是多少?
解:小桐这学期的体育成绩是
95×20%+90×30%+85×50%
20%+30%+50%
=19+27+42.5
=88.5.
再比试一次,怎么样?
活动五:当堂小结
(1)这节课我们学习的主要内容,你都理解了吗?
温故而知新哟
加权平均数的意义
数据的权的意义
加权平均数公式
权的三种表现形式
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
加权平均数公式
ω
n
+
+
…
ω
3
ω
2
ω
1
+
+
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
…
+
ω
n
x
n
+
权的三种表现形式
1、直接以数据形式给出;
2、比例形式给出;
3、百分数形式给出.
(2)布置作业:
1、必做题:教科书P121页第1题
2、选做题:教科书P116页练习
活动六:课后任务
23.1加权平均数
活动一:教学引入
问题1:
某市三个郊县的人均耕地面积如下表:
郊县
人均耕地面积/公顷
A
0.15
B
0.21
C
0.18
这个市郊县的人均耕地面积如下表示正确吗?
0.15+0.21+0.18
3
活动二:引例归纳
思考1:这个市郊县的人均耕地面积与哪些因素有关?它们之间有何关系?
人均耕地面积
总耕地面积
问题2
:某市三个郊县的人数及人均耕地面积如下表:
郊县
人数/万
人均耕地面积/公顷
A
15
0.15
B
7
0.21
C
10
0.18
人口总数
=
这个市郊县的人均耕地面积是多少?(精确到0.01公顷)
0.15×15
0.21×7
0.18×10
+
+
15+7+10
≈
0.17(公顷)
解答:这个市郊县的人均耕地面积是:
郊县
人数(万)
人均耕地面积(公顷)
A
15
0.15
B
7
0.21
C
10
0.18
思考2:总耕地面积
三个郊县耕地面积之和
思考3:人口总数
三个郊县人数之和
人均耕地面积
=
总耕地面积
人口总数
我们就把上面求得的平均数0.17称为三个数0.15、0.21、0.18的
加权平均数,由于各郊县的人数不同,各郊县的人均耕地面积对这个市郊县的人均耕地面积的影响就不同.因此我们把三个郊县的人数(单位:万)15、7、10分别称为三个数据的权.
“权”的英文是
Weight,有表示数据重要程度的意思.即数据的权能反映数据的相对“重要程度”.
特别提示
这很重要,好好理解哟
而有的同学求得这个市郊县的人均耕地面积为
x=
0.15+0.21+0.18
3
=0.18公顷.
显然是忽视了数据的权的作用,结论肯定是错误的.
郊县
人数(万)
人均耕地面积(公顷)
A
15
0.15
B
7
0.21
C
10
0.18
在上面的问题中,三个数据0.15、0.21、0.18的权分别是15、7、10,说明三个数据在计算这个市郊县人均耕地面积时的相对重要程度不同.
郊县
人数(万)
人均耕地面积(公顷)
A
B
C
x
1
x
2
x
3
思考:你能用上面的字母表示出这个市郊县的人均耕地面积吗?
ω
1
ω
2
ω
3
若三个数
、
、
的权分别为
、
、
,则这3个数的加权平均数为:
ω
1
x
2
x
1
x
3
ω
2
ω
3
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
ω
3
ω
2
ω
1
+
+
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
ω
3
ω
2
ω
1
+
+
若n个数
、
、
、…
、
的权分别为
、
、
、…
、
则这n个数的加权平均数为:
ω
n
x
n
ω
3
ω
1
ω
2
x
2
x
1
x
3
活动三:课堂举例
例1
一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3∶3∶2∶2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
思考(1)这家公司在招聘英文翻译时,对甲乙两名应试者进行了哪几方面的英语水平测试?成绩分别是多少?
思考(2)招口语能力较强的翻译,“听、说、读、写成绩按照3∶3∶2∶2的比确定”,说明公司侧重于哪几个方面的成绩?
思考(3)计算两名候选人的平均成绩实际上就是求两人听、说、读、写四项成绩的加权平均数,那么它们的权分别是什么?
认真思考,你一定行的.
解:(1)听、说、读、写的成绩按照3∶3∶2∶2的比确定,则甲的平均成绩为
85×3+83×3+78×2+75×2
3+3+2+2
=
81
乙的平均成绩为
73×3+80×3+85×2+82×2
3+3+2+2
=
79.3.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
仔细看,要记住正确的书写格式哟
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2∶2∶3∶3的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
思考(1)招笔译能力较强的翻译,“听、说、读、写成绩按照2∶2∶3∶3的比确定”,说明公司侧重于哪几个方面的成绩?
思考(2)计算两名候选人的平均成绩实际上就是求两人听、说、读、写四项成绩的加权平均数,那么它们的权分别是什么?
解:(2)听、说、读、写的成绩按照2∶2∶3∶3的比确定,则甲的平均成绩为
85×2+83×2+78×3+75×3
2+2+3+3
=
79.5
乙的平均成绩为
73×2+80×2+85×3+82×3
2+2+3+3
=
80.7
显然乙的成绩比甲的高,所以从成绩看,应该录取乙.
你掌握正确的书写格式了吗?
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
例2
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
思考(1)你认为在计算选手的综合成绩时侧重于哪个方面的成绩?三项成绩的权分别是多少?
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考(2)利用加权平均数公式你能求出甲、乙的综合成绩,决出两人的名次吗?
认真思考,一定能回答正确的。
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考两名选手的单项成绩都是两个95分与一个85分,为什么他们的最后得分不同?从中你能体会到权的作用吗?
选手A的95分是演讲能力,B的95分是演讲内容,而根据题意可知,演讲内容所占的权重比演讲能力所占的权重大,所以A的95分就不如B的95分在综合成绩中占的分值大.在此更能显示出“权”的重要性.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
你真正理解了吗?
活动四:当堂练习
1、某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如下表所示:
候选人
测试成绩(百分制)
面试
笔试
甲
86
90
乙
92
83
(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁将被录取?
解:(1)面试和笔试同等重
要时,甲的平均成绩为
86×5+90×5
5+5
=43+45
=88.
乙的平均成绩为
92×5+83×5
5+5
=46+41.5
=87.5.
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
候选人
测试成绩
(百分制)
面试
笔试
甲
86
90
乙
92
83
对比一下,你写的解题过程合理吗?
(2)面试和笔试分别赋予它们6和4的权,则甲的平均成绩为
86×6+90×4
6+4
=51.6+36
=87.6.
乙的平均成绩为
92×6+83×4
6+4
=55.2+33.2
=88.4.
显然乙的成绩比甲的高,所以从成绩看,应该录取乙.
候选人
测试成绩
(百分制)
面试
笔试
甲
86
90
乙
92
83
这次你的书写过程怎么样呢?
2、晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95分、90分、85分,小桐这学期的体育成绩是多少?
解:小桐这学期的体育成绩是
95×20%+90×30%+85×50%
20%+30%+50%
=19+27+42.5
=88.5.
再比试一次,怎么样?
活动五:当堂小结
(1)这节课我们学习的主要内容,你都理解了吗?
温故而知新哟
加权平均数的意义
数据的权的意义
加权平均数公式
权的三种表现形式
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
加权平均数公式
ω
n
+
+
…
ω
3
ω
2
ω
1
+
+
ω
1
x
1
ω
2
x
2
+
ω
3
x
3
+
…
+
ω
n
x
n
+
权的三种表现形式
1、直接以数据形式给出;
2、比例形式给出;
3、百分数形式给出.
(2)布置作业:
1、必做题:教科书P121页第1题
2、选做题:教科书P116页练习
活动六:课后任务
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
