冀教版数学七年级上册2.7 角的和与差 学案+当堂检测(含答案)
文档属性
| 名称 | 冀教版数学七年级上册2.7 角的和与差 学案+当堂检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览




文档简介
2.7
角的和与差
学习目标:
1.理解角的和差、角平分线的几何意义;(重点)
2.掌握角之间的和差关系,并能进行简单的计算;(难点)
3.了解余角与补角的概念,理解余角与补角的性质并会进行运用.(重点、难点)
学习重点:理解角的和差、角平分线的几何意义,了解补角和余角的概念.
学习难点:角的和差计算、余角及补角性质及其运用.
知识链接
线段的和与差
如图1,AC=_______+________;
BC=_______-_________;
AB=_______-_________.
2.线段的中点
如图1,若点B是线段AC的中点,则AB=_______=_________;AC=_____=________.
计算
45°26’40’’=_______°;
56.435°=___°____’_____’’
.
(
A
B
)4.等式的性质:等式的两边同时__________同一个数,等式仍然成立.
新知预习
角的和与差
如图2:∠AOB=∠
+∠
,∠AOC=∠
-∠
,
∠COB=∠
-∠
.
2.角的平分线
(1)
如图2,如果∠AOC=∠BOC,那么射线OC是∠AOB的角平分线.
角平分线的定义:_______________________________________________
符号语言:∵OC平分∠AOB
∴∠AOC=∠BOC
(∠AOB=2∠
或∠AOB
=2∠
;或∠AOC=∠
,∠BOC
=∠_____
)
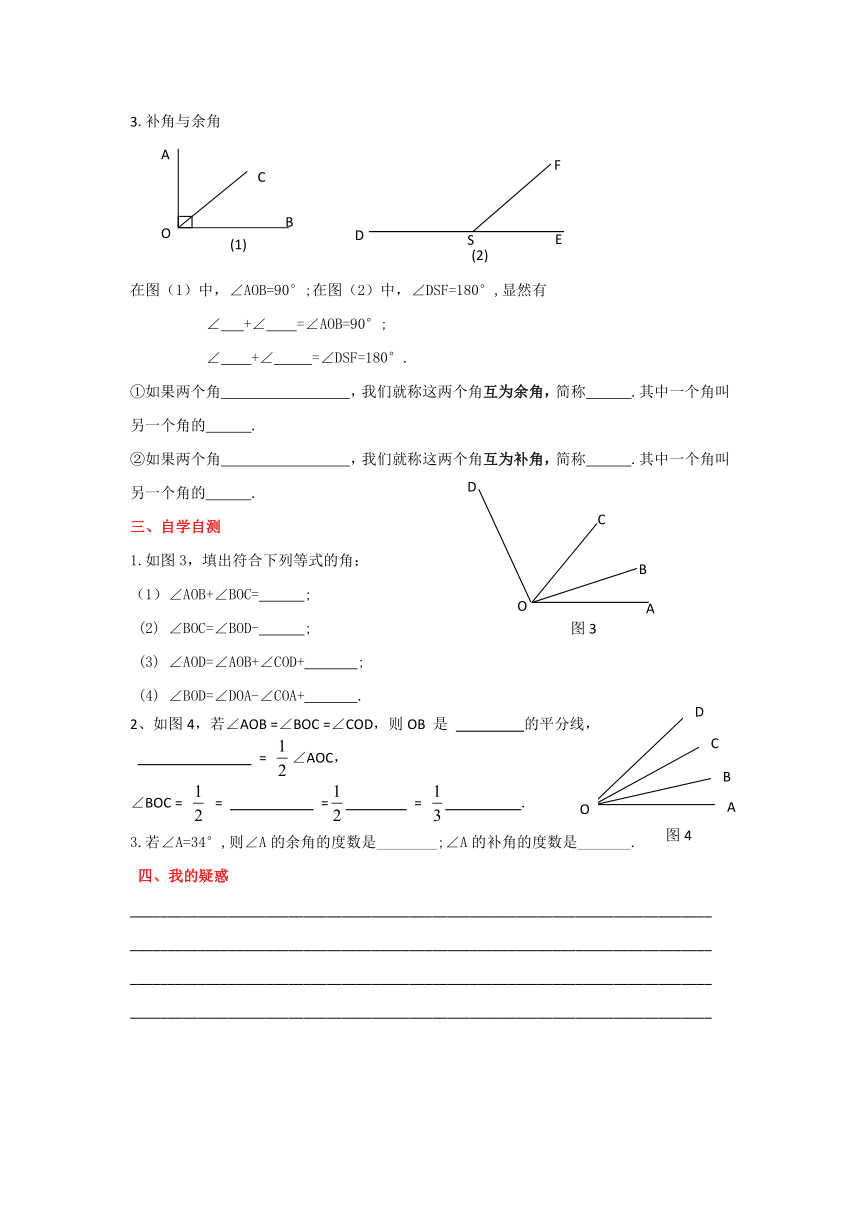
3.补角与余角
在图(1)中,∠AOB=90°;在图(2)中,∠DSF=180°,显然有
∠
+∠
=∠AOB=90°;
∠
+∠
=∠DSF=180°.
①如果两个角
,我们就称这两个角互为余角,简称
.其中一个角叫另一个角的
.
②如果两个角
,我们就称这两个角互为补角,简称
.其中一个角叫另一个角的
.
自学自测
1.如图3,填出符合下列等式的角:
(1)∠AOB+∠BOC=
;
(2)
∠BOC=∠BOD-
;
(3)
∠AOD=∠AOB+∠COD+
;
(4)
∠BOD=∠DOA-∠COA+
.
2、如图4,若∠AOB
=∠BOC
=∠COD,则OB
是
的平分线,
=
∠AOC,
∠BOC
=
=
=
=
.
3.若∠A=34°,则∠A的余角的度数是________;∠A的补角的度数是_______.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:角的和差关系及运算
例1:如图,已知∠AOC与∠BOD都是直角,∠BOC=51°.
(1)求∠AOD的度数.
(2)求∠AOB和∠DOC的度数.
(3)∠AOB与∠DOC有何大小关系?
【归纳总结】在利用角的和、差关系进行计算时,首先要弄清题意,理清各角之间的数量关系,用两个角的和或差表示第三个角,如果知道任意两个角的度数,第三个角的度数可以通过运算求出来.
例2:两个角的度数之比为7:3,它们的差为36°,求这两个角.
【归纳总结】根据题意,列出方程,求出这两个角的度数.
【针对训练】
1.已知∠AOB=138°,∠AOC=∠BOD=90°.求∠COD的度数.
2.已知∠AOB=120°,OC在它的内部,且把∠AOB分成1:3的两个角,那么∠AOC的度数为(
)
A.
40°
B.40°或80°
C.30°
D.30°或90°
探究点2:角的平分线的应用
例2:如图,O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
【归纳总结】解决这类问题,关键是根据角平分线得到相等的角,或求出一个较大的角,借助于某一个中间的角,把未知量转化为已知量.
【针对训练】
1.如图,射线OC平分∠AOD,射线OD平分∠COB,则下列结论错误的是( )
A.∠AOC=∠BOD
B.∠AOD=2∠BOD
C.∠BOC=2∠COD
D.∠AOB=2∠AOD
2.如图,已知∠AOB=120°,OM平分∠AOB,ON平分∠MOB,则∠AON=______.
探究点3:角的度、分、秒的计算
例3:计算:
(1)12°59′57″+57′58″;
(2)97°3′12″-1°45′53″.
【归纳总结】角的度、分、秒进行加、减运算时,度与度加、减,分与分加、减,秒与秒加、减.分秒相加时逢60要进位,相减时要借一作60.
注意:角的度、分、秒进行加减运算时,运算时需将单位化成一致,再进行运算.
【针对训练】
计算:
(1)103.3°+176°42′-98.34°.
(2)24°22′36″×3.
探究点4:补角与余角
合作探究
(1)图中给出的各角,那些互为补角?
(2)填下列表:
∠a
∠a的余角
∠a的补角
5°
32°
45°
77°
62°23′
x°
结论:同一个锐角的补角比它的余角大___________________.
(3)填空:
①70°的余角是
,补角是
.
②∠(∠
<90°)的它的余角是
,它的补角是
.
余角与补角的性质
如果∠1和∠2都是∠α的余角,那么∠1和∠2相等吗?试着说明理由.
解:因为∠1和∠2都是∠α的余角
所以∠1+∠α=
°,∠2+∠α=
°,
所以∠
+∠
=∠
+∠
,
所以∠
=∠
.
②如果∠3和∠4都是∠β的补角,那么∠3和∠4相等吗?试说明理由.
解:因为∠3和∠4都是∠β的补角
所以∠3+∠β=
°,∠4+∠β=
°,
所以∠
+∠
=∠
+∠
,
所以∠
=∠
.
由此得出结论:
.
例5:一个角的余角比这个角的补角的少20°,则这个角为(
)
A.30°
B.40°
C.60°
D.75°
【归纳总结】解有关互为余角或互为补角的问题时,除了要弄清楚它们的概念,通常情况下我们可以引进未知数来构造方程求解.
例6:如果∠AOB+∠BOC=90°,
∠BOC与∠COD互余,那么∠AOB和∠COD的关系是(
)
A.互余
B.互补
C.相等
D.不能确定
【归纳总结】同角(等角)的余角相等.
【针对训练】
1.若一个角的补角等于它的余角4倍,求这个角的度数.
2.如图,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?则∠3与∠2是什么关系?
二、课堂小结
内容
角的平分线
从一个角的顶点引出的一条______把这个角分成的两个角_____,那么这条射线叫做这个角的___________.
余角与补角
①如果两个角
,我们就称这两个角互为余角,简称
.其中一个角叫另一个角的
.
②如果两个角
,我们就称这两个角互为补角,简称
.其中一个角叫另一个角的
.
余角与补角的性质
_______(或______)的余角相等;
_______(或______)的补角相等.
1.点P在∠MAN内,现有如下等式:①∠PAM=∠MAN;②∠PAN=∠MAN;③∠PAM=∠PAN;④∠MAN=2∠PAN.其中能表示AP是角平分线的等式有(
)
A.1个
B.2个
C.3个
D.4个
2.如图,∠AOC=∠BOD=90°,下列结论中正确的个数是(
)
①∠AOB=∠COD ②∠AOD=3∠BOC
③∠AOD+∠BOC=∠AOC+∠BOD
A.0
B.1
C.2
D.3
3.如图,OD是∠AOC的平分线,OC是∠BOD的平分线,且∠COD=40°,则∠AOB=(
)
A.80°
B.100°
C.120°
D.160°
(第2题)
(第3题)
4.一个锐角的补角比这个角的余角大
(
)
A.30?
B.45?
C.60?
D.90?
5.如图,已知∠BOD=2∠AOB,OC是∠AOD的平分线,则下列四个结论:①∠BOC=∠AOB;②∠DOC=2∠BOC;③∠BOC=∠AOB;④∠DOC=3∠BOC.其中正确的是(
)
A.①②
B.③④
C.②③
D.①④
6.若∠1与∠2互为补角,且∠1<∠2,则∠1的余角是
(
)
A.∠1
B.∠1+∠2
C.(∠1+∠2)
D.(∠2-∠1)
7.已知∠与∠互补,且∠=35?18′,则∠=________.
8.如图,点O是直线AB上一点,已知∠BOD=30°,OE平分∠AOD,那么∠AOE的度数是____.
9.如图,OC平分∠AOB,OD平分∠AOC,OE平分∠BOC,则图中与∠AOD相等的角有___个,与∠AOC相等的角有___个.
10.如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=80°,那么∠BOC=_______;
(2)如果∠AOC=80°,∠COE=50°,那么∠BOD=____.
(第8题)
(第9题)
(第10题)
11.如图,直线AB,CD交于点O,OB平分∠DOE.如果∠COE=80°,求∠EOB与∠AOC的度数.
12.如图,∠COD是平角,∠AOC=40°,∠BOD=50°,OM,ON分别是∠AOC,∠BOD的平分线,求∠MON的度数.
13..如图,∠AOB=90?,∠AOC=30?,且OM平分∠BOC,
ON平分∠AOC,
(1)求∠MON的度数.
(2)若∠AOB=α其他条件不变,求∠MON的度数.
(3)若∠AOC=β(β为锐角)其他条件不变,求∠MON的度数
(4)从上面结果中看出有什么规律?
当堂检测参考答案:
D
2.C
3.C
4.D
5.B
6.D
7.144°42’
8.75°
9.3
2
10.
40°
65°
11.【解】 ∵∠COE=80°,AB,CD交于点O,
∴∠EOD=180°-∠COE=100°.
∵OB平分∠EOD,
∴∠EOB=∠BOD=∠EOD=50°,
∴∠AOC=∠BOD=50°.
12.【解】 ∵OM,ON分别是∠AOC,∠BOD的平分线,
∴∠MOC=∠AOC=×40°=20°,
∠NOD=∠BOD=×50°=25°.
又∵∠COD是平角,
∴∠MOC+∠MON+∠NOD=180°,
∴20°+∠MON+25°=180°,
∴∠MON=135°.
13.(1)∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°
∵OM平分∠BOC,ON平分∠AOC
∴∠COM=60°,∠CON=15°
∴∠MON=∠COM-∠CON=45°.
(2)∵∠AOB=α,∠AOC=30°,
∴∠BOC=α+30°
∵OM平分∠BOC,ON平分∠AOC
∴∠COM=+15°,∠CON=15°
∴∠MON=∠COM-∠CON=
.
(3)∵∠AOB=90°,∠AOC=β,
∴∠BOC=90°+β
∵OM平分∠BOC,ON平分∠AOC
∴∠COM=45°+
,∠CON=
.
∴∠MON=∠COM-∠CON=45°.
(4)从上面的结果中,发现:
∠MON的大小只和∠AOB得大小有关,与∠A0C的大小无关.
角的和与差
学习目标:
1.理解角的和差、角平分线的几何意义;(重点)
2.掌握角之间的和差关系,并能进行简单的计算;(难点)
3.了解余角与补角的概念,理解余角与补角的性质并会进行运用.(重点、难点)
学习重点:理解角的和差、角平分线的几何意义,了解补角和余角的概念.
学习难点:角的和差计算、余角及补角性质及其运用.
知识链接
线段的和与差
如图1,AC=_______+________;
BC=_______-_________;
AB=_______-_________.
2.线段的中点
如图1,若点B是线段AC的中点,则AB=_______=_________;AC=_____=________.
计算
45°26’40’’=_______°;
56.435°=___°____’_____’’
.
(
A
B
)4.等式的性质:等式的两边同时__________同一个数,等式仍然成立.
新知预习
角的和与差
如图2:∠AOB=∠
+∠
,∠AOC=∠
-∠
,
∠COB=∠
-∠
.
2.角的平分线
(1)
如图2,如果∠AOC=∠BOC,那么射线OC是∠AOB的角平分线.
角平分线的定义:_______________________________________________
符号语言:∵OC平分∠AOB
∴∠AOC=∠BOC
(∠AOB=2∠
或∠AOB
=2∠
;或∠AOC=∠
,∠BOC
=∠_____
)
3.补角与余角
在图(1)中,∠AOB=90°;在图(2)中,∠DSF=180°,显然有
∠
+∠
=∠AOB=90°;
∠
+∠
=∠DSF=180°.
①如果两个角
,我们就称这两个角互为余角,简称
.其中一个角叫另一个角的
.
②如果两个角
,我们就称这两个角互为补角,简称
.其中一个角叫另一个角的
.
自学自测
1.如图3,填出符合下列等式的角:
(1)∠AOB+∠BOC=
;
(2)
∠BOC=∠BOD-
;
(3)
∠AOD=∠AOB+∠COD+
;
(4)
∠BOD=∠DOA-∠COA+
.
2、如图4,若∠AOB
=∠BOC
=∠COD,则OB
是
的平分线,
=
∠AOC,
∠BOC
=
=
=
=
.
3.若∠A=34°,则∠A的余角的度数是________;∠A的补角的度数是_______.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:角的和差关系及运算
例1:如图,已知∠AOC与∠BOD都是直角,∠BOC=51°.
(1)求∠AOD的度数.
(2)求∠AOB和∠DOC的度数.
(3)∠AOB与∠DOC有何大小关系?
【归纳总结】在利用角的和、差关系进行计算时,首先要弄清题意,理清各角之间的数量关系,用两个角的和或差表示第三个角,如果知道任意两个角的度数,第三个角的度数可以通过运算求出来.
例2:两个角的度数之比为7:3,它们的差为36°,求这两个角.
【归纳总结】根据题意,列出方程,求出这两个角的度数.
【针对训练】
1.已知∠AOB=138°,∠AOC=∠BOD=90°.求∠COD的度数.
2.已知∠AOB=120°,OC在它的内部,且把∠AOB分成1:3的两个角,那么∠AOC的度数为(
)
A.
40°
B.40°或80°
C.30°
D.30°或90°
探究点2:角的平分线的应用
例2:如图,O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
【归纳总结】解决这类问题,关键是根据角平分线得到相等的角,或求出一个较大的角,借助于某一个中间的角,把未知量转化为已知量.
【针对训练】
1.如图,射线OC平分∠AOD,射线OD平分∠COB,则下列结论错误的是( )
A.∠AOC=∠BOD
B.∠AOD=2∠BOD
C.∠BOC=2∠COD
D.∠AOB=2∠AOD
2.如图,已知∠AOB=120°,OM平分∠AOB,ON平分∠MOB,则∠AON=______.
探究点3:角的度、分、秒的计算
例3:计算:
(1)12°59′57″+57′58″;
(2)97°3′12″-1°45′53″.
【归纳总结】角的度、分、秒进行加、减运算时,度与度加、减,分与分加、减,秒与秒加、减.分秒相加时逢60要进位,相减时要借一作60.
注意:角的度、分、秒进行加减运算时,运算时需将单位化成一致,再进行运算.
【针对训练】
计算:
(1)103.3°+176°42′-98.34°.
(2)24°22′36″×3.
探究点4:补角与余角
合作探究
(1)图中给出的各角,那些互为补角?
(2)填下列表:
∠a
∠a的余角
∠a的补角
5°
32°
45°
77°
62°23′
x°
结论:同一个锐角的补角比它的余角大___________________.
(3)填空:
①70°的余角是
,补角是
.
②∠(∠
<90°)的它的余角是
,它的补角是
.
余角与补角的性质
如果∠1和∠2都是∠α的余角,那么∠1和∠2相等吗?试着说明理由.
解:因为∠1和∠2都是∠α的余角
所以∠1+∠α=
°,∠2+∠α=
°,
所以∠
+∠
=∠
+∠
,
所以∠
=∠
.
②如果∠3和∠4都是∠β的补角,那么∠3和∠4相等吗?试说明理由.
解:因为∠3和∠4都是∠β的补角
所以∠3+∠β=
°,∠4+∠β=
°,
所以∠
+∠
=∠
+∠
,
所以∠
=∠
.
由此得出结论:
.
例5:一个角的余角比这个角的补角的少20°,则这个角为(
)
A.30°
B.40°
C.60°
D.75°
【归纳总结】解有关互为余角或互为补角的问题时,除了要弄清楚它们的概念,通常情况下我们可以引进未知数来构造方程求解.
例6:如果∠AOB+∠BOC=90°,
∠BOC与∠COD互余,那么∠AOB和∠COD的关系是(
)
A.互余
B.互补
C.相等
D.不能确定
【归纳总结】同角(等角)的余角相等.
【针对训练】
1.若一个角的补角等于它的余角4倍,求这个角的度数.
2.如图,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?则∠3与∠2是什么关系?
二、课堂小结
内容
角的平分线
从一个角的顶点引出的一条______把这个角分成的两个角_____,那么这条射线叫做这个角的___________.
余角与补角
①如果两个角
,我们就称这两个角互为余角,简称
.其中一个角叫另一个角的
.
②如果两个角
,我们就称这两个角互为补角,简称
.其中一个角叫另一个角的
.
余角与补角的性质
_______(或______)的余角相等;
_______(或______)的补角相等.
1.点P在∠MAN内,现有如下等式:①∠PAM=∠MAN;②∠PAN=∠MAN;③∠PAM=∠PAN;④∠MAN=2∠PAN.其中能表示AP是角平分线的等式有(
)
A.1个
B.2个
C.3个
D.4个
2.如图,∠AOC=∠BOD=90°,下列结论中正确的个数是(
)
①∠AOB=∠COD ②∠AOD=3∠BOC
③∠AOD+∠BOC=∠AOC+∠BOD
A.0
B.1
C.2
D.3
3.如图,OD是∠AOC的平分线,OC是∠BOD的平分线,且∠COD=40°,则∠AOB=(
)
A.80°
B.100°
C.120°
D.160°
(第2题)
(第3题)
4.一个锐角的补角比这个角的余角大
(
)
A.30?
B.45?
C.60?
D.90?
5.如图,已知∠BOD=2∠AOB,OC是∠AOD的平分线,则下列四个结论:①∠BOC=∠AOB;②∠DOC=2∠BOC;③∠BOC=∠AOB;④∠DOC=3∠BOC.其中正确的是(
)
A.①②
B.③④
C.②③
D.①④
6.若∠1与∠2互为补角,且∠1<∠2,则∠1的余角是
(
)
A.∠1
B.∠1+∠2
C.(∠1+∠2)
D.(∠2-∠1)
7.已知∠与∠互补,且∠=35?18′,则∠=________.
8.如图,点O是直线AB上一点,已知∠BOD=30°,OE平分∠AOD,那么∠AOE的度数是____.
9.如图,OC平分∠AOB,OD平分∠AOC,OE平分∠BOC,则图中与∠AOD相等的角有___个,与∠AOC相等的角有___个.
10.如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=80°,那么∠BOC=_______;
(2)如果∠AOC=80°,∠COE=50°,那么∠BOD=____.
(第8题)
(第9题)
(第10题)
11.如图,直线AB,CD交于点O,OB平分∠DOE.如果∠COE=80°,求∠EOB与∠AOC的度数.
12.如图,∠COD是平角,∠AOC=40°,∠BOD=50°,OM,ON分别是∠AOC,∠BOD的平分线,求∠MON的度数.
13..如图,∠AOB=90?,∠AOC=30?,且OM平分∠BOC,
ON平分∠AOC,
(1)求∠MON的度数.
(2)若∠AOB=α其他条件不变,求∠MON的度数.
(3)若∠AOC=β(β为锐角)其他条件不变,求∠MON的度数
(4)从上面结果中看出有什么规律?
当堂检测参考答案:
D
2.C
3.C
4.D
5.B
6.D
7.144°42’
8.75°
9.3
2
10.
40°
65°
11.【解】 ∵∠COE=80°,AB,CD交于点O,
∴∠EOD=180°-∠COE=100°.
∵OB平分∠EOD,
∴∠EOB=∠BOD=∠EOD=50°,
∴∠AOC=∠BOD=50°.
12.【解】 ∵OM,ON分别是∠AOC,∠BOD的平分线,
∴∠MOC=∠AOC=×40°=20°,
∠NOD=∠BOD=×50°=25°.
又∵∠COD是平角,
∴∠MOC+∠MON+∠NOD=180°,
∴20°+∠MON+25°=180°,
∴∠MON=135°.
13.(1)∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°
∵OM平分∠BOC,ON平分∠AOC
∴∠COM=60°,∠CON=15°
∴∠MON=∠COM-∠CON=45°.
(2)∵∠AOB=α,∠AOC=30°,
∴∠BOC=α+30°
∵OM平分∠BOC,ON平分∠AOC
∴∠COM=+15°,∠CON=15°
∴∠MON=∠COM-∠CON=
.
(3)∵∠AOB=90°,∠AOC=β,
∴∠BOC=90°+β
∵OM平分∠BOC,ON平分∠AOC
∴∠COM=45°+
,∠CON=
.
∴∠MON=∠COM-∠CON=45°.
(4)从上面的结果中,发现:
∠MON的大小只和∠AOB得大小有关,与∠A0C的大小无关.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
