第二章 整式的加减 数学活动 课件(共32张PPT)
文档属性
| 名称 | 第二章 整式的加减 数学活动 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 19:19:53 | ||
图片预览






文档简介
(共32张PPT)
人教版七年级数学上册
·上课课件
第二章
整式的加减
数学活动
新课导入
导入课题
本节课我们将通过两个数学活动体验如何将本章所学的“整式加减”的相关知识应用于生产、生活实际之中.
学习目标
(1)用整式和整式的加减运算表示实际问题中的数量关系.
(2)体会从特殊到一般,从个体到整体来观察、分析问题的方法,尝试从不同角度探究问题,提升应用意识和创新意识.
推进新课
活动1
探索用火柴棍摆的三角形
(1)如图所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2、3或4个三角形,分别需要多少根火柴棍,如果图形中含有n个三角形,需要多少根火柴棍?
观察图形时的角度不同,规律的显现方式,得到的表达形式也就不同,下面提供几种不同的思路(或方法)供同学们参考.
三角形个数
1
2
3
4
…
n
火柴棍根数
3
3+2
3+2×2
3+2×3
…
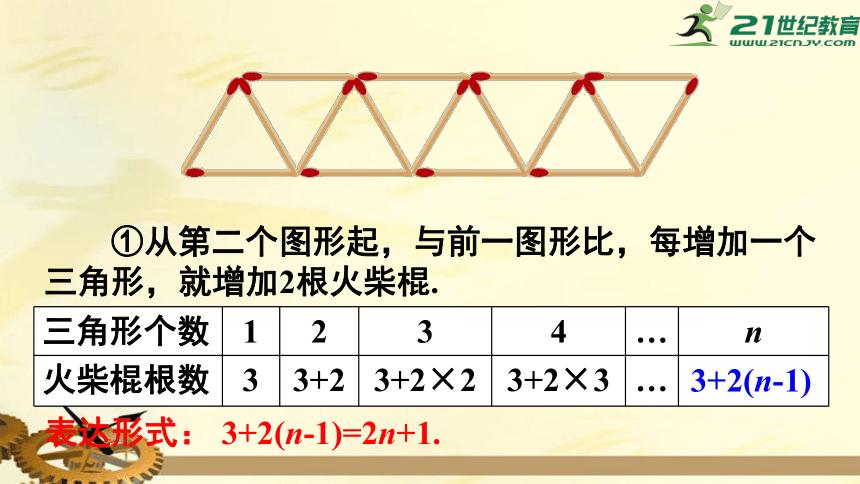
①从第二个图形起,与前一图形比,每增加一个三角形,就增加2根火柴棍.
表达形式:
3+2(n-1)=2n+1.
3+2(n-1)
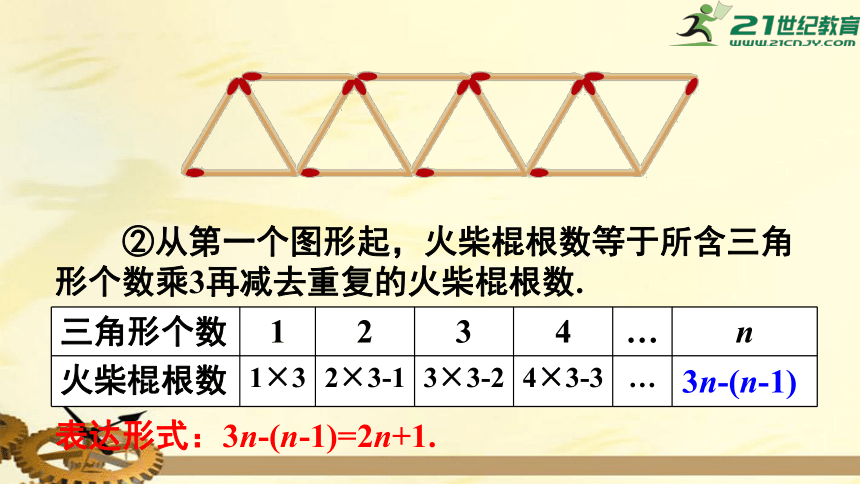
②从第一个图形起,火柴棍根数等于所含三角形个数乘3再减去重复的火柴棍根数.
三角形个数
1
2
3
4
…
n
火柴棍根数
1×3
2×3-1
3×3-2
4×3-3
…
3n-(n-1)
表达形式:3n-(n-1)=2n+1.
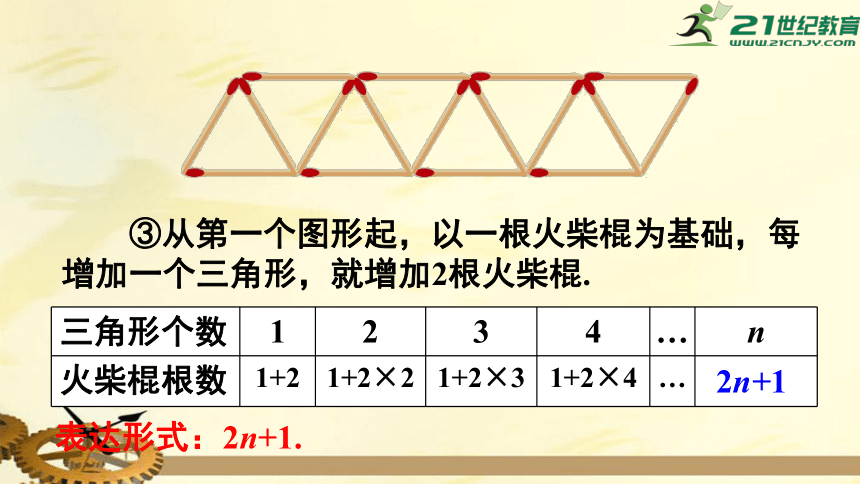
③从第一个图形起,以一根火柴棍为基础,每增加一个三角形,就增加2根火柴棍.
三角形个数
1
2
3
4
…
n
火柴棍根数
1+2
1+2×2
1+2×3
1+2×4
…
2n+1
表达形式:2n+1.
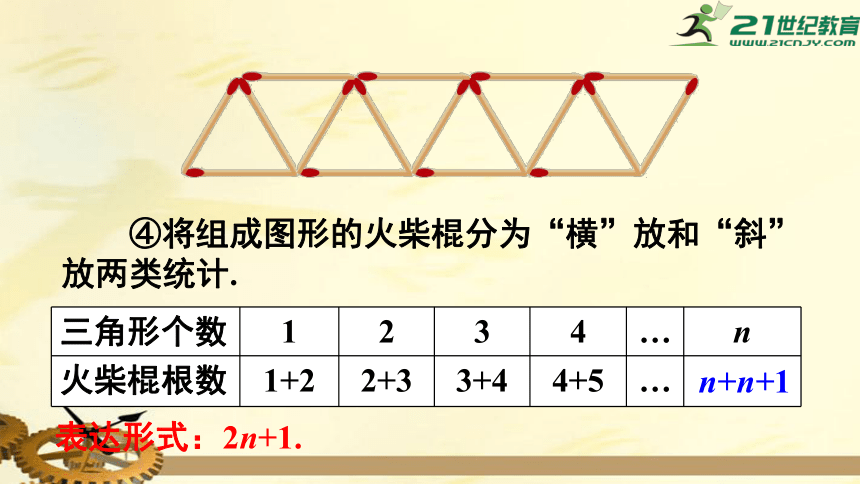
④将组成图形的火柴棍分为“横”放和“斜”放两类统计.
三角形个数
1
2
3
4
…
n
火柴棍根数
1+2
2+3
3+4
4+5
…
n+n+1
表达形式:2n+1.
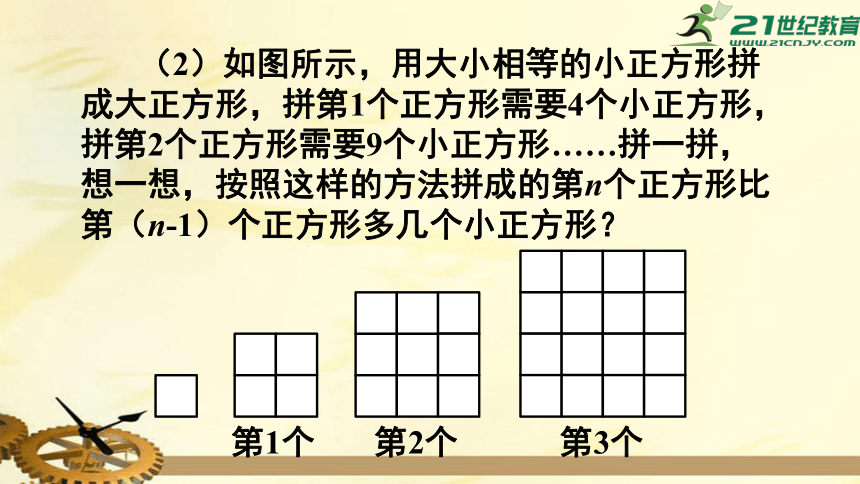
(2)如图所示,用大小相等的小正方形拼成大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个小正方形?
第1个
第2个
第3个
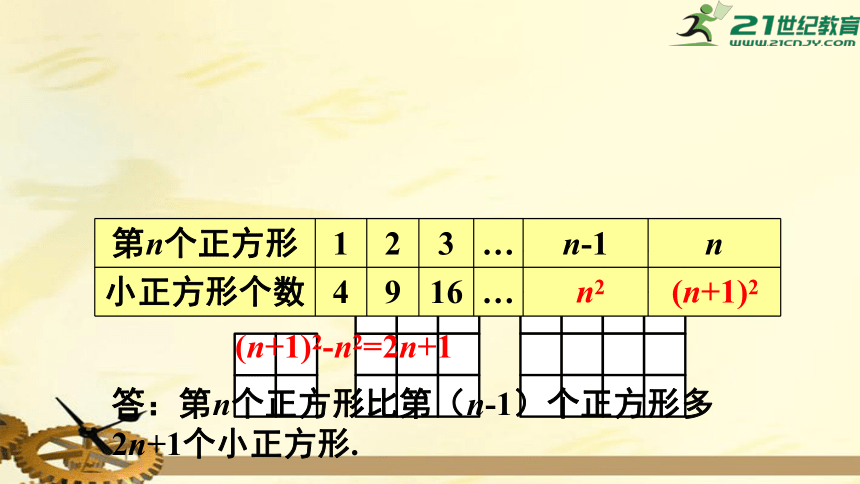
第n个正方形
1
2
3
…
n-1
n
小正方形个数
4
9
16
…
n2
(n+1)2
(n+1)2-n2=2n+1
答:第n个正方形比第(n-1)个正方形多2n+1个小正方形.
活动2
探索怎样买笔记本省钱
一种笔记本售价是2.3元/本,如果一次买100本以上(不含100本),售价是2.2元/本.列式表示买n本笔记本所需钱数(注意对n的大小要有所考虑).请同学们讨论下面的问题:
(1)按照这种售价规定,会不会出现多买比少买反而付钱少的情况?
(2)如果需要100本笔记本,怎样购买能省钱?
(3)了解实际生活中类似问题,并举出几个具体例子.
笔记本个数
n(n≤100)
n(n>100)
所需钱数
2.3n
2.2n
解:(1)当n=99时,所需钱数为
2.3×99=227.7(元)
当n=101时,所需钱数为
2.2×101=222.2(元)
222.2<227.7
答:买101本比买99本付钱少.
解:(2)当n=100时,所需钱数为
2.3×100=230(元)
222.2<230
答:买101本比较省钱.
笔记本个数
n(n≤100)
n(n>100)
所需钱数
2.3n
2.2n
活动3
探索月历中的数字规律
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
图是某月的月历.
(1)带阴影的方框中的9个数之和与方框正中心的数有什么关系?
带阴影的方框中9个数之和是99,是正中心数11的9倍.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(2)如果将带阴影的方框移至如图的位置,(1)中的关系还成立吗?
带阴影的方框中9个数之和是144,是正中心数16的9倍.
(3)不改变带阴影的方框的大小,将方框移动几个位置试一试,你能得出什么结论?你能证明这个结论吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
设日历中间的某数为a,则月历中数的排列规律:
1.行:从左向右,依次递增1.
2.
列:从上向下,依次递增7.
3.对角线:从左上向右下,依次递增8.
a
a–8
a+8
a–7
a+7
a
a–1
a+1
a
a–6
a+8
a–1
a+7
a+1
a–7
a
a–8
a+6
a–8+a–7+a–6+a–1+a+a+1+a+6+a+7+a+8=9a
(4)这个结论对于任何一个月的月历都成立吗?
成立
(5)如图,如果带阴影的方框里的数是4个,你能得出什么结论?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a–1
a+7
a
a+6
a+1
a+8
a
a+7
a(a+6)–(a–1)(a+7)=7
(a+1)(a+7)–a(a+8)=7
右上对角线的乘积比左下对角线的乘积大7.
a+(a+6)=(a–1)+(a+7)
(a+1)+(a+7)=a+(a+8)
两条斜对角线的和相等
(6)如图,对于带阴影的框中的4个数,又能得出什么结论?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a–7
a
a–6
a–1
a
a+7
a+1
a+6
(a–1)+(a–6)=a+(a–7)
(a+1)+(a+6)=a+(a+7)
中间两个数的和与两边两个数的和相等.
(a–1)(a–6)–a(a–7)=6
(a+1)(a+6)–a(a+7)=6
中间两个数的乘积比两边两个数的乘积大6.
随堂演练
基础巩固
观察下列一组数:
,
,
,
,…,第n
个数是________.
2.
如图所示,以一根火柴棍为一边,用火柴棍拼成一排由正方形组成的图形,如果图形中含有n个正方形,需要多少根火柴棍?
3n+1
拓展延伸
3.
若干个偶数排列成如下图所示,探究方框中数之间的关系.
20
36
52
解:右边的框中,设中间的数为a,则上面的数为a–16,下面的数为a+16,三数和为3a.
中间的框中,设左上角数字为b,则右上角数字为(b+2),左下数字为(b+16),右下数字为(b+18).四数和为4b+36,且左上+右下=右上+左下.
24
38
40
12
14
16
28
30
32
44
46
48
右边的框,设中间的数为c,则有
c–18
c–16
c–14
c–2
c
c+2
c+14
c+16
c+18
九数和为9c,且两斜对角线上的数的和相等.
课堂小结
表达形式:2n+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
带阴影的方框中9个数之和是正中心数的9倍.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
人教版七年级数学上册
·上课课件
第二章
整式的加减
数学活动
新课导入
导入课题
本节课我们将通过两个数学活动体验如何将本章所学的“整式加减”的相关知识应用于生产、生活实际之中.
学习目标
(1)用整式和整式的加减运算表示实际问题中的数量关系.
(2)体会从特殊到一般,从个体到整体来观察、分析问题的方法,尝试从不同角度探究问题,提升应用意识和创新意识.
推进新课
活动1
探索用火柴棍摆的三角形
(1)如图所示,用火柴棍拼成一排由三角形组成的图形,如果图形中含有2、3或4个三角形,分别需要多少根火柴棍,如果图形中含有n个三角形,需要多少根火柴棍?
观察图形时的角度不同,规律的显现方式,得到的表达形式也就不同,下面提供几种不同的思路(或方法)供同学们参考.
三角形个数
1
2
3
4
…
n
火柴棍根数
3
3+2
3+2×2
3+2×3
…
①从第二个图形起,与前一图形比,每增加一个三角形,就增加2根火柴棍.
表达形式:
3+2(n-1)=2n+1.
3+2(n-1)
②从第一个图形起,火柴棍根数等于所含三角形个数乘3再减去重复的火柴棍根数.
三角形个数
1
2
3
4
…
n
火柴棍根数
1×3
2×3-1
3×3-2
4×3-3
…
3n-(n-1)
表达形式:3n-(n-1)=2n+1.
③从第一个图形起,以一根火柴棍为基础,每增加一个三角形,就增加2根火柴棍.
三角形个数
1
2
3
4
…
n
火柴棍根数
1+2
1+2×2
1+2×3
1+2×4
…
2n+1
表达形式:2n+1.
④将组成图形的火柴棍分为“横”放和“斜”放两类统计.
三角形个数
1
2
3
4
…
n
火柴棍根数
1+2
2+3
3+4
4+5
…
n+n+1
表达形式:2n+1.
(2)如图所示,用大小相等的小正方形拼成大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n-1)个正方形多几个小正方形?
第1个
第2个
第3个
第n个正方形
1
2
3
…
n-1
n
小正方形个数
4
9
16
…
n2
(n+1)2
(n+1)2-n2=2n+1
答:第n个正方形比第(n-1)个正方形多2n+1个小正方形.
活动2
探索怎样买笔记本省钱
一种笔记本售价是2.3元/本,如果一次买100本以上(不含100本),售价是2.2元/本.列式表示买n本笔记本所需钱数(注意对n的大小要有所考虑).请同学们讨论下面的问题:
(1)按照这种售价规定,会不会出现多买比少买反而付钱少的情况?
(2)如果需要100本笔记本,怎样购买能省钱?
(3)了解实际生活中类似问题,并举出几个具体例子.
笔记本个数
n(n≤100)
n(n>100)
所需钱数
2.3n
2.2n
解:(1)当n=99时,所需钱数为
2.3×99=227.7(元)
当n=101时,所需钱数为
2.2×101=222.2(元)
222.2<227.7
答:买101本比买99本付钱少.
解:(2)当n=100时,所需钱数为
2.3×100=230(元)
222.2<230
答:买101本比较省钱.
笔记本个数
n(n≤100)
n(n>100)
所需钱数
2.3n
2.2n
活动3
探索月历中的数字规律
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
图是某月的月历.
(1)带阴影的方框中的9个数之和与方框正中心的数有什么关系?
带阴影的方框中9个数之和是99,是正中心数11的9倍.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(2)如果将带阴影的方框移至如图的位置,(1)中的关系还成立吗?
带阴影的方框中9个数之和是144,是正中心数16的9倍.
(3)不改变带阴影的方框的大小,将方框移动几个位置试一试,你能得出什么结论?你能证明这个结论吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
设日历中间的某数为a,则月历中数的排列规律:
1.行:从左向右,依次递增1.
2.
列:从上向下,依次递增7.
3.对角线:从左上向右下,依次递增8.
a
a–8
a+8
a–7
a+7
a
a–1
a+1
a
a–6
a+8
a–1
a+7
a+1
a–7
a
a–8
a+6
a–8+a–7+a–6+a–1+a+a+1+a+6+a+7+a+8=9a
(4)这个结论对于任何一个月的月历都成立吗?
成立
(5)如图,如果带阴影的方框里的数是4个,你能得出什么结论?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a–1
a+7
a
a+6
a+1
a+8
a
a+7
a(a+6)–(a–1)(a+7)=7
(a+1)(a+7)–a(a+8)=7
右上对角线的乘积比左下对角线的乘积大7.
a+(a+6)=(a–1)+(a+7)
(a+1)+(a+7)=a+(a+8)
两条斜对角线的和相等
(6)如图,对于带阴影的框中的4个数,又能得出什么结论?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a–7
a
a–6
a–1
a
a+7
a+1
a+6
(a–1)+(a–6)=a+(a–7)
(a+1)+(a+6)=a+(a+7)
中间两个数的和与两边两个数的和相等.
(a–1)(a–6)–a(a–7)=6
(a+1)(a+6)–a(a+7)=6
中间两个数的乘积比两边两个数的乘积大6.
随堂演练
基础巩固
观察下列一组数:
,
,
,
,…,第n
个数是________.
2.
如图所示,以一根火柴棍为一边,用火柴棍拼成一排由正方形组成的图形,如果图形中含有n个正方形,需要多少根火柴棍?
3n+1
拓展延伸
3.
若干个偶数排列成如下图所示,探究方框中数之间的关系.
20
36
52
解:右边的框中,设中间的数为a,则上面的数为a–16,下面的数为a+16,三数和为3a.
中间的框中,设左上角数字为b,则右上角数字为(b+2),左下数字为(b+16),右下数字为(b+18).四数和为4b+36,且左上+右下=右上+左下.
24
38
40
12
14
16
28
30
32
44
46
48
右边的框,设中间的数为c,则有
c–18
c–16
c–14
c–2
c
c+2
c+14
c+16
c+18
九数和为9c,且两斜对角线上的数的和相等.
课堂小结
表达形式:2n+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
带阴影的方框中9个数之和是正中心数的9倍.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
