2.2.3 整式的加减 课件(共24张PPT)
文档属性
| 名称 | 2.2.3 整式的加减 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 19:30:19 | ||
图片预览







文档简介
(共24张PPT)
第二章
整式的加减
2.2
整式的加减
第3课时
整式的加减
人教版七年级数学上册
·上课课件
新课导入
导入课题
前面我们学习了合并同类项,去括号等知识,它们是进行整式加减运算的基础,这节课我们来学习整式的加减运算.
任意写一个两位数
交换它的十位
数字与个位数字,又得到一个数
两个数相加
小组游戏
重复几次看看,谁能先发现这些和有什么规律?对于任意一个两位数都成立吗?
学习目标
【知识与技能】
让学生从实际背景中去体会进行整式的加减的必要性,并能灵活运用整式的加减的步骤进行运算.
【过程与方法】
培养学生的观察、分析、归纳、总结以及概括能力.
【情感态度】
认识到数学是解决实际问题和进行交流的重要工具.
【教学重点】
整式的加减.
【教学难点】
总结出整式的加减的一般步骤.
推进新课
知识点1
整式的加减
例6
计算
(1)(
2x
–
3y
)
+
(
5x
+
4y
)
=
2x
–
3y
+
5x
+
4y
=
7x
+
y
(2)(
8a
–
7b
)
–
(
4a
–
5b
)
=
8a
–
7b
–
4a
+5b
=
4a
–
2b
例7
笔记本的单价是x元,圆珠笔的单价是y元.
小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解法1:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元):
(3x+2y)
+
(4x+3y)
=
7x+5y
解法2:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元):
(3x+4x)
+
(2y+3y)
=
7x+5y
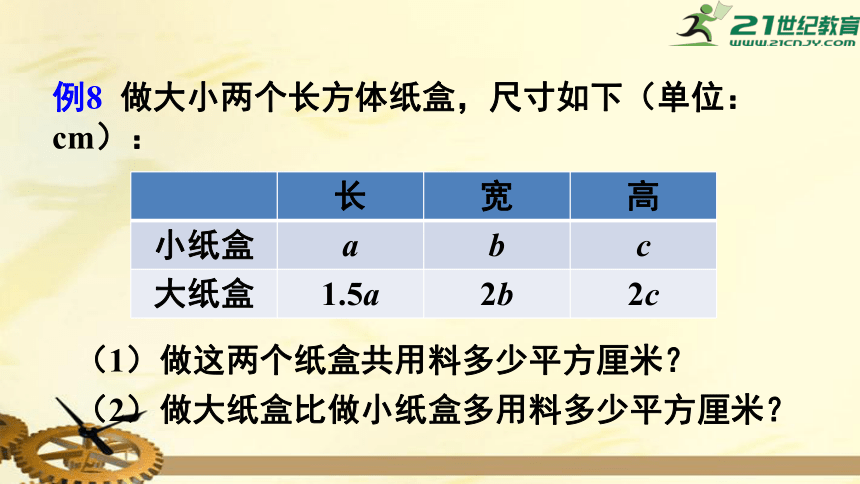
例8
做大小两个长方体纸盒,尺寸如下(单位:
cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是(6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料(单位:cm2):
(2ab+2bc+2ca)+
(6ab+8bc+6ca)
=
8ab+10bc+8ca
(2)做大纸盒比做小纸盒多用料(单位:cm2)
(6ab+8bc+6ca)-
(2ab+2bc+2ca)
=4ab+6bc+4ca
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
例9
求
的值,其中
x
=
–
2,y
=
.
当x=
–
2,y
=
时,原式
先将式子化简,再代入数值进行计算比较简便.
练习1
计算
巩固练习
(1)3xy
–
4xy
–(–
2xy)
=
3xy
–
4xy
+
2xy
=
xy
练习2
计算
(1)(
–
x
+
2x2
+
5)+(4x2
–
3
–
6x)
=
–
x
+
2x2
+
5
+
4x2
–
3
–
6x
=
6x2
–7x
+
2
(2)(
3a2
–
ab
+
7)–(–
4a2
+
2ab
+
7)
=3a2
–
ab
+
7+
4a2
–
2ab
–
7
=7a2
–
3ab
练习3
计算先化简下式,再求值.
5(3a2b
–
ab2)–(ab2+3a2b),
解:原式=
15a2b
–
5ab2
–
ab2
–
3a2b
=
12a2b
–
6ab2
其中
,
.
当
,
时
原式=
随堂演练
基础巩固
1.
计算:
(1)(5a
+
4c
+
7b)+(5c
–
3b
–
6a)
解:原式=
5a
+
4c
+
7b
+
5c
–
3b
–
6a
=
–
a
+
4b
+
9c
(2)(8xy
–
x2
+
y2)–(x2
–
y2
+
8xy)
解:原式=
8xy
–
x2
+
y2
–
x2
+
y2
–
8xy
=
–
2x2
+
2y2
(3)(2x2
–
+
3x)–
4(x
–
x2
+
)
解:原式=
2x2
–
+
3x
–
4x
+
4x2
–
2
=
6x2
–
x
–
(4)3x2
–[7x
–(4x
–
3)–
2x2]
解:原式=
3x2
–(7x
–
4x
+
3
–
2x2)
=
3x2
–
7x
+
4x
–
3
+
2x2
=
5x2
–
3x
–
3
综合应用
2.
窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.
已知下部小正方形的边长是a
cm,计算:
(1)窗户的面积;
(2)窗户外框的总长.
解:(1)窗户的面积为
+4a2=
(cm2)
(2)窗户的外框总长是:
πa+2a×3=πa+6a
=(π+6)a(cm)
3.
观察下列图形并填表(单位:cm).
梯形个数
1
2
3
4
5
6
…
n
图形周长
5a
8a
11a
…
14a
17a
20a
(3n+2)a
拓展延伸
4.
(1)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数.
解:(1)10b
+
a;
(2)列式表示上面的两位数与10的乘积.
(2)10(10b
+
a);
(3)列式表示(1)中的两位数与它的10倍的和,这个和是11的倍数吗?为什么?
(3)10b
+
a
+
10(10b
+
a)=
11(10b
+
a),这个和是11的倍数,因为它含有11这个因数.
课堂小结
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二章
整式的加减
2.2
整式的加减
第3课时
整式的加减
人教版七年级数学上册
·上课课件
新课导入
导入课题
前面我们学习了合并同类项,去括号等知识,它们是进行整式加减运算的基础,这节课我们来学习整式的加减运算.
任意写一个两位数
交换它的十位
数字与个位数字,又得到一个数
两个数相加
小组游戏
重复几次看看,谁能先发现这些和有什么规律?对于任意一个两位数都成立吗?
学习目标
【知识与技能】
让学生从实际背景中去体会进行整式的加减的必要性,并能灵活运用整式的加减的步骤进行运算.
【过程与方法】
培养学生的观察、分析、归纳、总结以及概括能力.
【情感态度】
认识到数学是解决实际问题和进行交流的重要工具.
【教学重点】
整式的加减.
【教学难点】
总结出整式的加减的一般步骤.
推进新课
知识点1
整式的加减
例6
计算
(1)(
2x
–
3y
)
+
(
5x
+
4y
)
=
2x
–
3y
+
5x
+
4y
=
7x
+
y
(2)(
8a
–
7b
)
–
(
4a
–
5b
)
=
8a
–
7b
–
4a
+5b
=
4a
–
2b
例7
笔记本的单价是x元,圆珠笔的单价是y元.
小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解法1:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元):
(3x+2y)
+
(4x+3y)
=
7x+5y
解法2:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元):
(3x+4x)
+
(2y+3y)
=
7x+5y
例8
做大小两个长方体纸盒,尺寸如下(单位:
cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是(6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料(单位:cm2):
(2ab+2bc+2ca)+
(6ab+8bc+6ca)
=
8ab+10bc+8ca
(2)做大纸盒比做小纸盒多用料(单位:cm2)
(6ab+8bc+6ca)-
(2ab+2bc+2ca)
=4ab+6bc+4ca
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
例9
求
的值,其中
x
=
–
2,y
=
.
当x=
–
2,y
=
时,原式
先将式子化简,再代入数值进行计算比较简便.
练习1
计算
巩固练习
(1)3xy
–
4xy
–(–
2xy)
=
3xy
–
4xy
+
2xy
=
xy
练习2
计算
(1)(
–
x
+
2x2
+
5)+(4x2
–
3
–
6x)
=
–
x
+
2x2
+
5
+
4x2
–
3
–
6x
=
6x2
–7x
+
2
(2)(
3a2
–
ab
+
7)–(–
4a2
+
2ab
+
7)
=3a2
–
ab
+
7+
4a2
–
2ab
–
7
=7a2
–
3ab
练习3
计算先化简下式,再求值.
5(3a2b
–
ab2)–(ab2+3a2b),
解:原式=
15a2b
–
5ab2
–
ab2
–
3a2b
=
12a2b
–
6ab2
其中
,
.
当
,
时
原式=
随堂演练
基础巩固
1.
计算:
(1)(5a
+
4c
+
7b)+(5c
–
3b
–
6a)
解:原式=
5a
+
4c
+
7b
+
5c
–
3b
–
6a
=
–
a
+
4b
+
9c
(2)(8xy
–
x2
+
y2)–(x2
–
y2
+
8xy)
解:原式=
8xy
–
x2
+
y2
–
x2
+
y2
–
8xy
=
–
2x2
+
2y2
(3)(2x2
–
+
3x)–
4(x
–
x2
+
)
解:原式=
2x2
–
+
3x
–
4x
+
4x2
–
2
=
6x2
–
x
–
(4)3x2
–[7x
–(4x
–
3)–
2x2]
解:原式=
3x2
–(7x
–
4x
+
3
–
2x2)
=
3x2
–
7x
+
4x
–
3
+
2x2
=
5x2
–
3x
–
3
综合应用
2.
窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形.
已知下部小正方形的边长是a
cm,计算:
(1)窗户的面积;
(2)窗户外框的总长.
解:(1)窗户的面积为
+4a2=
(cm2)
(2)窗户的外框总长是:
πa+2a×3=πa+6a
=(π+6)a(cm)
3.
观察下列图形并填表(单位:cm).
梯形个数
1
2
3
4
5
6
…
n
图形周长
5a
8a
11a
…
14a
17a
20a
(3n+2)a
拓展延伸
4.
(1)一个两位数的个位上的数是a,十位上的数是b,列式表示这个两位数.
解:(1)10b
+
a;
(2)列式表示上面的两位数与10的乘积.
(2)10(10b
+
a);
(3)列式表示(1)中的两位数与它的10倍的和,这个和是11的倍数吗?为什么?
(3)10b
+
a
+
10(10b
+
a)=
11(10b
+
a),这个和是11的倍数,因为它含有11这个因数.
课堂小结
通过上面的学习,我们可以得到整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
