2021-2022学年数学九年级上册-华东师大版第24章 解直角三角形 单元测试卷(word含答案)
文档属性
| 名称 | 2021-2022学年数学九年级上册-华东师大版第24章 解直角三角形 单元测试卷(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 424.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 23:17:23 | ||
图片预览




文档简介
第24章
解直角三角形
单元测试卷-2021-2022学年数学九年级上册-华师大版(含答案)
一、单选题(共15题,共计45分)
1、如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为(??
)
A.21cm??????B.14cm??????C.6cm??????D.24cm
2、如图,直线AB与⊙O相切于点A,⊙O的半径为1,若∠OBA=30°,则OB长为(??
)
A.1??????B.2??????C.
??????D.2
3、在△ABC中,∠A=120°,∠B=45°,∠C=15°,则cosB等于( )
A.
??????B.
??????C.
??????D.
4、如图1,A,B两点被池塘隔开,在AB外任选一点C,连结AC,
BC分别取其三等分点M、N.量得MN=38m.则AB的长是?
(??????
)
A.152m??????B.114m??????C.76m??????D.104m
5、如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=
,则边BC的长为(??
)
A.30
cm??????B.20
cm??????C.10
cm??????D.5
cm
6、sin30°的值为(??
)
A.
??????B.
??????C.
??????D.
7、如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于(?
?)
A.
??????B.
??????C.
??????D.
8、已知:在Rt△ABC中,∠C=90°,sinA=
,
则cosB的值为( )
A.
??????B.
??????C.
??????D.
9、如果平行四边形两邻边的长分别为3,4,那么其对角线的长可能是(??
).
A.1??????B.3??????C.7??????D.9
10、如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张????????B.第5张???????C.第6张???????D.第7张
11、下列长度的三根木棒首尾相接,能做成三角形框架的是(??
)
A.13cm、7cm、5cm??????B.5cm、7cm、3cm????????C.7cm、5cm、12cm??????D.5cm、15cm、9cm
12、如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为(
??)
A.
??????B.2
??????C.
??????D.3
13、如图,在⊙O中,直径CD⊥弦
于点
,连接
,已知⊙
的半径为2,
,则∠
的大小为(??????
)
A.30°??????B.45°??????C.60°??????D.15°
14、已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+
=0的根的情况是(?????
)
A.有两个相等的实数根??????B.有两个不相等的实数根??????C.没有实数根??????D.无法确定
15、如图,在
中,
,
,
,则
的长为(?
)
A.2??????B.4??????C.6??????D.8
二、填空题(共10题,共计30分)
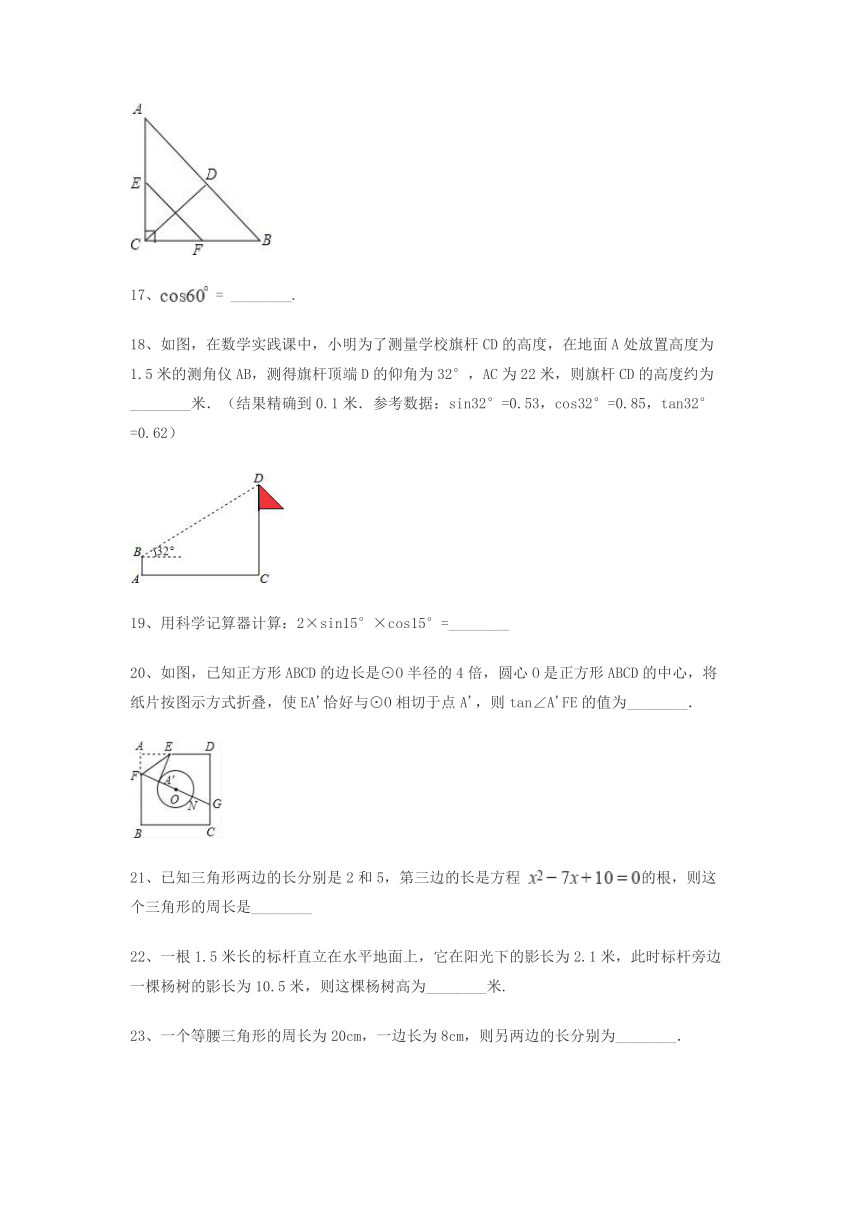
16、如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若EF=8,则CD的长为?________.
17、
=
________.
18、如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,则旗杆CD的高度约为________米.(结果精确到0.1米.参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62)
19、用科学记算器计算:2×sin15°×cos15°=________?
20、如图,已知正方形ABCD的边长是⊙O半径的4倍,圆心O是正方形ABCD的中心,将纸片按图示方式折叠,使EA'恰好与⊙O相切于点A',则tan∠A'FE的值为________.
21、已知三角形两边的长分别是2和5,第三边的长是方程
的根,则这个三角形的周长是________
22、一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米,此时标杆旁边一棵杨树的影长为10.5米,则这棵杨树高为________米.
23、一个等腰三角形的周长为20cm,一边长为8cm,则另两边的长分别为________.
24、如图,已知
的半径为
,点A,B在
上,
动点C在
上(与A,B两点不重合),连接BC点D是BC中点,连接AD则线段AD的最大值为________.
25、一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为________米.
三、解答题(共5题,共计25分)
26、先化简,再求值:(1﹣
)÷
,其中x=2sin45°+1.
27、小宇想测量位于池塘两端的A,B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A,B两点的距离.
28、州政府投资3个亿拟建的恩施民族高中,它位于北纬31°,教学楼窗户朝南,窗户高度为h米,此地一年的冬至这一天的正午时刻太阳光与地面的夹角最小为α,夏至这一天的正午时刻太阳光与地面的夹角最大为β.若你是一名设计师,请你为教学楼的窗户设计一个直角形遮阳蓬BCD,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内(如图).根据测量测得∠α=32.6°,∠β=82.5°,h=2.2米.请你求出直角形遮阳蓬BCD中BC与CD的长各是多少?(结果精确到0.1米)
(参考数据:sin32.6°=0.54,sin82.5°=0.99,tan32.6°=0.64,tan82.5°=7.60)
29、如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.
≈1.414,
≈1.732).
30、某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测昌平中心公园的仿古建筑“弘文阁”AB的高度.他们先在点C处用高1.5米的测角仪CE测得“弘文阁”顶A的仰角为30°,然后向“弘文阁”的方向前进18m到达D处,在点D处测得“弘文阁”顶A的仰角为50°.求“弘文阁”AB的高(结果精确到0.1m,参考数据:,tan50°≈1.19,tan40°≈0.84,
).
参考答案
一、单选题(共15题,共计45分)
1、A
2、B
3、D
4、B
5、C
6、A
7、C
8、B
9、B
10、B
11、B
12、C
13、A
14、B
15、C
二、填空题(共10题,共计30分)
16、
17、
18、
19、
20、
21、
22、
23、
24、
25、
三、解答题(共5题,共计25分)
26、
27、
28、
29、
30、
解直角三角形
单元测试卷-2021-2022学年数学九年级上册-华师大版(含答案)
一、单选题(共15题,共计45分)
1、如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为(??
)
A.21cm??????B.14cm??????C.6cm??????D.24cm
2、如图,直线AB与⊙O相切于点A,⊙O的半径为1,若∠OBA=30°,则OB长为(??
)
A.1??????B.2??????C.
??????D.2
3、在△ABC中,∠A=120°,∠B=45°,∠C=15°,则cosB等于( )
A.
??????B.
??????C.
??????D.
4、如图1,A,B两点被池塘隔开,在AB外任选一点C,连结AC,
BC分别取其三等分点M、N.量得MN=38m.则AB的长是?
(??????
)
A.152m??????B.114m??????C.76m??????D.104m
5、如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=
,则边BC的长为(??
)
A.30
cm??????B.20
cm??????C.10
cm??????D.5
cm
6、sin30°的值为(??
)
A.
??????B.
??????C.
??????D.
7、如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于(?
?)
A.
??????B.
??????C.
??????D.
8、已知:在Rt△ABC中,∠C=90°,sinA=
,
则cosB的值为( )
A.
??????B.
??????C.
??????D.
9、如果平行四边形两邻边的长分别为3,4,那么其对角线的长可能是(??
).
A.1??????B.3??????C.7??????D.9
10、如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张????????B.第5张???????C.第6张???????D.第7张
11、下列长度的三根木棒首尾相接,能做成三角形框架的是(??
)
A.13cm、7cm、5cm??????B.5cm、7cm、3cm????????C.7cm、5cm、12cm??????D.5cm、15cm、9cm
12、如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为(
??)
A.
??????B.2
??????C.
??????D.3
13、如图,在⊙O中,直径CD⊥弦
于点
,连接
,已知⊙
的半径为2,
,则∠
的大小为(??????
)
A.30°??????B.45°??????C.60°??????D.15°
14、已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+
=0的根的情况是(?????
)
A.有两个相等的实数根??????B.有两个不相等的实数根??????C.没有实数根??????D.无法确定
15、如图,在
中,
,
,
,则
的长为(?
)
A.2??????B.4??????C.6??????D.8
二、填空题(共10题,共计30分)
16、如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若EF=8,则CD的长为?________.
17、
=
________.
18、如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,则旗杆CD的高度约为________米.(结果精确到0.1米.参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62)
19、用科学记算器计算:2×sin15°×cos15°=________?
20、如图,已知正方形ABCD的边长是⊙O半径的4倍,圆心O是正方形ABCD的中心,将纸片按图示方式折叠,使EA'恰好与⊙O相切于点A',则tan∠A'FE的值为________.
21、已知三角形两边的长分别是2和5,第三边的长是方程
的根,则这个三角形的周长是________
22、一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米,此时标杆旁边一棵杨树的影长为10.5米,则这棵杨树高为________米.
23、一个等腰三角形的周长为20cm,一边长为8cm,则另两边的长分别为________.
24、如图,已知
的半径为
,点A,B在
上,
动点C在
上(与A,B两点不重合),连接BC点D是BC中点,连接AD则线段AD的最大值为________.
25、一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为________米.
三、解答题(共5题,共计25分)
26、先化简,再求值:(1﹣
)÷
,其中x=2sin45°+1.
27、小宇想测量位于池塘两端的A,B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A,B两点的距离.
28、州政府投资3个亿拟建的恩施民族高中,它位于北纬31°,教学楼窗户朝南,窗户高度为h米,此地一年的冬至这一天的正午时刻太阳光与地面的夹角最小为α,夏至这一天的正午时刻太阳光与地面的夹角最大为β.若你是一名设计师,请你为教学楼的窗户设计一个直角形遮阳蓬BCD,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内(如图).根据测量测得∠α=32.6°,∠β=82.5°,h=2.2米.请你求出直角形遮阳蓬BCD中BC与CD的长各是多少?(结果精确到0.1米)
(参考数据:sin32.6°=0.54,sin82.5°=0.99,tan32.6°=0.64,tan82.5°=7.60)
29、如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.
≈1.414,
≈1.732).
30、某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测昌平中心公园的仿古建筑“弘文阁”AB的高度.他们先在点C处用高1.5米的测角仪CE测得“弘文阁”顶A的仰角为30°,然后向“弘文阁”的方向前进18m到达D处,在点D处测得“弘文阁”顶A的仰角为50°.求“弘文阁”AB的高(结果精确到0.1m,参考数据:,tan50°≈1.19,tan40°≈0.84,
).
参考答案
一、单选题(共15题,共计45分)
1、A
2、B
3、D
4、B
5、C
6、A
7、C
8、B
9、B
10、B
11、B
12、C
13、A
14、B
15、C
二、填空题(共10题,共计30分)
16、
17、
18、
19、
20、
21、
22、
23、
24、
25、
三、解答题(共5题,共计25分)
26、
27、
28、
29、
30、
