2021-2022学年华东师大版数学九年级上册第21章 二次根式 章末测试(word含答案)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级上册第21章 二次根式 章末测试(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 634.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 23:19:30 | ||
图片预览




文档简介
第21章
二次根式
章末测试
(时间:90分钟
满分120分)
一、单选题(每小题3分,共36分)
1.下列各式是二次根式的是(
)
A.
B.
C.
D.
2.已知,那么a应满足什么条件
( )
A.a>0
B.a≥0
C.a
=0
D.a任何实数
3.等式成立的条件是(
)
A.
B.且
C.
D.
4.下列计算正确的是(
)
A.
B.
C.
D.
5.化简二次根式得(
)
A.
B.
C.
D.
6.估计的值应在(
)
A.和之间
B.和之间
C.和之间
D.和之间
7.已知m=﹣,如图,在数轴上表示实数m的点可能是( )
A.P
B.Q
C.R
D.S
8.关于8的叙述正确的是(
)
A.是最简二次根式
B.
C.不能与合并
D.与最接近的整数是3
9.下列式子与可以进行合并的是(
)
A.
B.
C.
D.
10.已知:a=,b=,则a与b的关系是(
)
A.a-b=0
B.a+b=0
C.ab=1
D.a2=b2
11.已知,则、、、的大小关系是(
)
A.
B.
C.
D.
12.古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是,,,记,那么三角形的面积为.如图,在中,,,所对的边分别记为,,,若,,,则的面积为(
)
A.14
B.20
C.
D.
二、填空题(每小题3分,共24分)
13.函数自变量的取值范围是______.
14.若,且a、b是两个连续的整数,则=______
15.设a,b,c是△ABC的三边的长,化简+|b﹣a﹣c|的结果是________.
16.若的整数部分为x,小数部分为y,则的值是________.
17.对于任意不相等的两个实数x,y,定义一种运算“☆”:x☆y=,根据这一规则,那么8☆(3☆10)=_______.
18.把面积为2平方单位的正方形按如图所示放置在数轴上,点A所表示的数为,现以点B为圆心,长为半径画弧,交数轴于点E,则点E所表示的数是________.
19.如图,在中,,底边,线段AB的垂直平分线交BC于点E,则的周长为__________.
20.如果正方形BEFG的面积为5,正方形ABCD的面积为7,则三角形AGC的面积____________.
三、解答题(本大题共60分)
21.(10分)计算:
(1)
(2)
22.(6分)已知,求代数式的值.
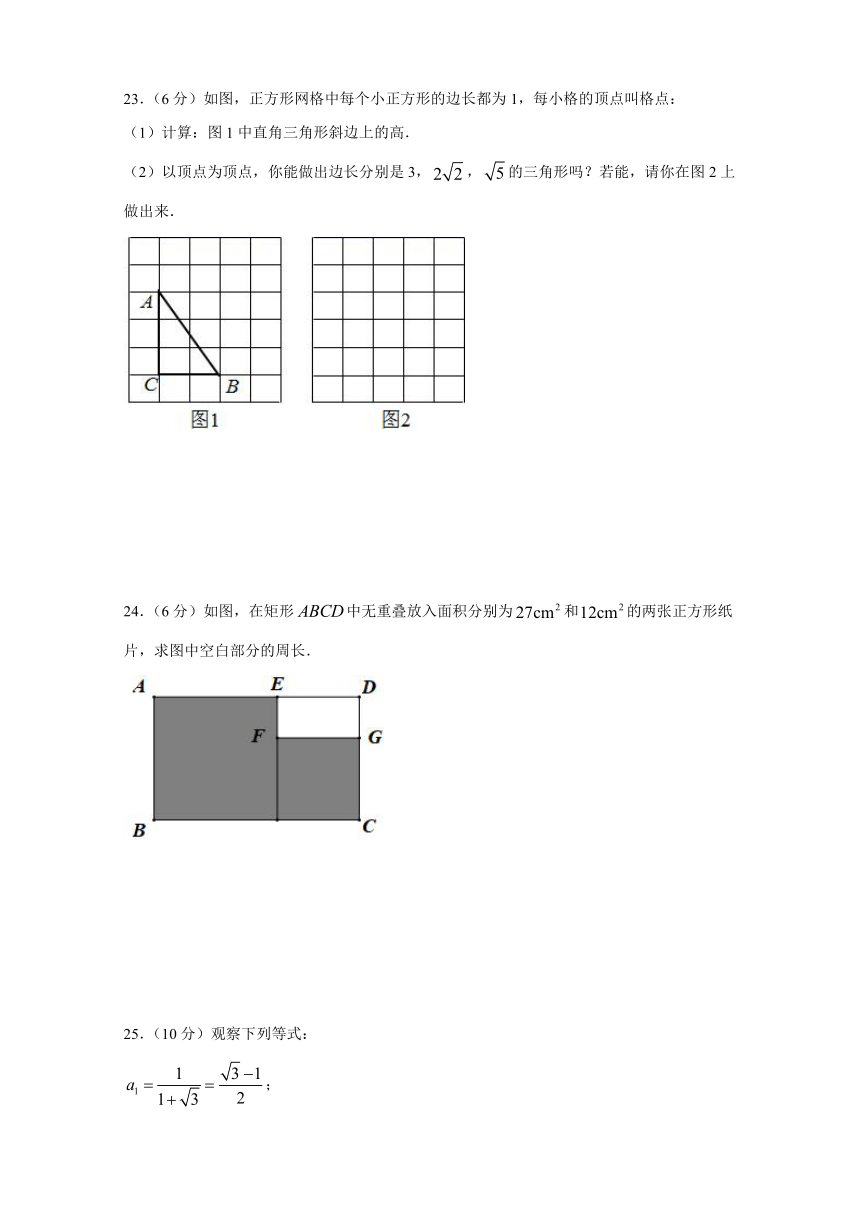
23.(6分)如图,正方形网格中每个小正方形的边长都为1,每小格的顶点叫格点:
(1)计算:图1中直角三角形斜边上的高.
(2)以顶点为顶点,你能做出边长分别是3,,的三角形吗?若能,请你在图2上做出来.
24.(6分)如图,在矩形中无重叠放入面积分别为和的两张正方形纸片,求图中空白部分的周长.
25.(10分)观察下列等式:
;
;
;
按照上述规律,回答以下问题:
(1)请写出第6个等式:________________;
(2)请写出第n个等式:________________;
(3)求的值.
26.(10分)已知直角三角形的两直角边分别是a、b,斜边是c,斜边上的高是h.
(1)如果a=﹣2,b=+2,求c的值;
(2)如果b=6,c=2,求直角三角形的面积及h的值.
27.(12分)如图,已知为等腰直角三角形,且,为上一点,且,过作且,连接.
(1)如图1,已知,连接、,求的面积;
(2)如图2所示,为上一点,连接,作交于点,求证:;
(3)已知面积为,为射线上一点,作,交射线于,连接,点为的中点,当有最小值时,请直接写出的面积.
参考答案
1.B
解:A:在中,,不合题意,故错误;
B:在中,,符合题意,故正确;
C:在中,的正负性不可确定,不合题意,故错误;
D:在中,根指数是3,不合题意,故错误;
故答案是:B.
2.B
解:∵的被开方数a的取值范围是,的被开方数中a的取值范围是任意实数,
故a应满足的条件是,
故选:B.
3.D
解:根据题意得,,
∴,
∴
故选D.
4.B
解:,
∴A选项不符合题意;
,
∴B选项符合题意;
,
∴C选项不符合题意;
,
∴D选项不符合题意.
综上,B选项符合题意,
故选:B.
5.A
解:∵,
∴,
∴.
故选A.
6.C
解:
<<
<<
故选:
7.B
解:m=﹣=
﹣=,
∵4<5<9,
∴2<<3,
∴﹣3<<﹣2,
∴﹣3<<﹣2.
故选:B.
8.D
解:A、,故不是最简二次根式,故错误;
B、,故错误;
C、,故错误;
D、,故与最接近的整数是3,故正确;
故选:D.
9.B
解:
A选项,,不符合题意;
B选项,,符合题意;
C选项,,不符合题意;
D选项,,不符合题意.
故选B.
10.C
解:分母有理化,可得a=2+,b=2-,
∴a-b=(2+)-(2-)=2,故A选项错误,不符合题意;
a+b=(2+)+(2-)=4,故B选项错误,不符合题意;
ab=(2+)×(2-)=4-3=1,故C选项正确,符合题意;
∵a2=(2+)2=4+4+3=7+4,b2=(2-)2=4-4+3=7-4,
∴a2≠b2,故D选项错误,不符合题意;
故选:C.
11.C
解:∵0<x<1,
∴设,
则;
;
;
∵,
∴;
故选:C.
12.C
解:∵,,,
∴,
∴的面积,
故选:C.
13.
解:∵,
∴,
∴;
故答案为:.
14.
解:∵,且a、b是两个连续的整数
∴
∴a=2,b=3,
∴==
故答案为:.
15.2a+2c
解:∵a,b,c是△ABC的三边的长,
∴a+c>b,a+b+c>0,
∴b﹣a﹣c<0,
∴+|b﹣a﹣c|=|a+b+c|+|b﹣a﹣c|=a+b+c+a+c-b=2a+2c.
故答案是:2a+2c.
16.
解:∵9<13<16,
∴,
∴,
∴,
∴x=2,y=,
∴==,
故答案为:.
17.
解:根据题中的新定义得:3☆10=,
则8☆(3☆10)=8☆6=
故答案为:.
18.2-+
解:∵正方形ABCD面积为2,
∴边长AB=AD=,对角线BD=2,
由作图可知:BE=BD=2,
∵点A所表示的数为,即OA=,
∴OB=OA-AB=-,
∴OE=BE-OB=2-(-)=2-+,
∴点E表示的数为2-+,
故答案为:2-+.
19.2+2
解:∵DE垂直平分AB,∠B=∠C=30°,
∴BE=AE,∠B=∠BAE=30°,
∴∠CAE=180°-∠B-∠BAE-∠C
=90°,
在Rt△CAE中,∠C=30°,
∴EC=2AE,
∴AE+EC=BE+EC=BC=2,即3AE=2,
∴AE=,EC=,
∴AC=,
∴∴△ACE的周长=AC+AE+CE=AC+BC=2+2,
故答案为:2+2.
20.
解:∵正方形ABCD的面积为7,正方形BEFG的面积为5,
∴BG=BE=,AB=BC=,
∴AG=AB-BG=-,
∴S△AGC=?AG?BC==,
故答案为:.
21.(1)2;(2)9
(1)解:
(2)
=
=9.
22..
解:原式,
,
,
将代入得:原式.
23.(1);(2)能,见解析
解:(1)设斜边上的高为h,
根据勾股定理:AB2=AC2+BC2;
∴,;
∴.
解得;
(2)能,作图如下:
24.
解:∵两张正方形纸片的面积分别为和,
∴它们的边长分别为,.
∴,
∴空白部分的周长.
25.(1);(2);(3)
解:(1)观察,如的下标3,与中被开方数,5和7得出:3×2-1=5,3×2+1=7,即7等于下标的2倍加1,5等于下标的2倍减1;
,
故答案是:;
(2)由(1)知,第n个等式的下标是n,被开方数分别为2n+1,2n-1,所以第n个等式
,
故答案是:;
(3)
.
26.(1);(2),
解:(1)由勾股定理及题意得:
;
(2)∵b=6,c=2,
∴,
∴,
∵,
∴.
27.(1);(2)见解析;(3)
解:(1)由题意可知
∵,
∴
,
∵为等腰直角三角形,
∴,
∴,
∵也是等腰直角三角形,
∴,,
∴,
∴,
∵,
∴,
作交于点,
∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∴,
∴,
∴,
如图,设
则
∵
;
(3)由(2)可知,
,
∴,
当重合时,时,最小,此时重合,
∵且,
∴此时为的中点,
∵,
∴
.
二次根式
章末测试
(时间:90分钟
满分120分)
一、单选题(每小题3分,共36分)
1.下列各式是二次根式的是(
)
A.
B.
C.
D.
2.已知,那么a应满足什么条件
( )
A.a>0
B.a≥0
C.a
=0
D.a任何实数
3.等式成立的条件是(
)
A.
B.且
C.
D.
4.下列计算正确的是(
)
A.
B.
C.
D.
5.化简二次根式得(
)
A.
B.
C.
D.
6.估计的值应在(
)
A.和之间
B.和之间
C.和之间
D.和之间
7.已知m=﹣,如图,在数轴上表示实数m的点可能是( )
A.P
B.Q
C.R
D.S
8.关于8的叙述正确的是(
)
A.是最简二次根式
B.
C.不能与合并
D.与最接近的整数是3
9.下列式子与可以进行合并的是(
)
A.
B.
C.
D.
10.已知:a=,b=,则a与b的关系是(
)
A.a-b=0
B.a+b=0
C.ab=1
D.a2=b2
11.已知,则、、、的大小关系是(
)
A.
B.
C.
D.
12.古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是,,,记,那么三角形的面积为.如图,在中,,,所对的边分别记为,,,若,,,则的面积为(
)
A.14
B.20
C.
D.
二、填空题(每小题3分,共24分)
13.函数自变量的取值范围是______.
14.若,且a、b是两个连续的整数,则=______
15.设a,b,c是△ABC的三边的长,化简+|b﹣a﹣c|的结果是________.
16.若的整数部分为x,小数部分为y,则的值是________.
17.对于任意不相等的两个实数x,y,定义一种运算“☆”:x☆y=,根据这一规则,那么8☆(3☆10)=_______.
18.把面积为2平方单位的正方形按如图所示放置在数轴上,点A所表示的数为,现以点B为圆心,长为半径画弧,交数轴于点E,则点E所表示的数是________.
19.如图,在中,,底边,线段AB的垂直平分线交BC于点E,则的周长为__________.
20.如果正方形BEFG的面积为5,正方形ABCD的面积为7,则三角形AGC的面积____________.
三、解答题(本大题共60分)
21.(10分)计算:
(1)
(2)
22.(6分)已知,求代数式的值.
23.(6分)如图,正方形网格中每个小正方形的边长都为1,每小格的顶点叫格点:
(1)计算:图1中直角三角形斜边上的高.
(2)以顶点为顶点,你能做出边长分别是3,,的三角形吗?若能,请你在图2上做出来.
24.(6分)如图,在矩形中无重叠放入面积分别为和的两张正方形纸片,求图中空白部分的周长.
25.(10分)观察下列等式:
;
;
;
按照上述规律,回答以下问题:
(1)请写出第6个等式:________________;
(2)请写出第n个等式:________________;
(3)求的值.
26.(10分)已知直角三角形的两直角边分别是a、b,斜边是c,斜边上的高是h.
(1)如果a=﹣2,b=+2,求c的值;
(2)如果b=6,c=2,求直角三角形的面积及h的值.
27.(12分)如图,已知为等腰直角三角形,且,为上一点,且,过作且,连接.
(1)如图1,已知,连接、,求的面积;
(2)如图2所示,为上一点,连接,作交于点,求证:;
(3)已知面积为,为射线上一点,作,交射线于,连接,点为的中点,当有最小值时,请直接写出的面积.
参考答案
1.B
解:A:在中,,不合题意,故错误;
B:在中,,符合题意,故正确;
C:在中,的正负性不可确定,不合题意,故错误;
D:在中,根指数是3,不合题意,故错误;
故答案是:B.
2.B
解:∵的被开方数a的取值范围是,的被开方数中a的取值范围是任意实数,
故a应满足的条件是,
故选:B.
3.D
解:根据题意得,,
∴,
∴
故选D.
4.B
解:,
∴A选项不符合题意;
,
∴B选项符合题意;
,
∴C选项不符合题意;
,
∴D选项不符合题意.
综上,B选项符合题意,
故选:B.
5.A
解:∵,
∴,
∴.
故选A.
6.C
解:
<<
<<
故选:
7.B
解:m=﹣=
﹣=,
∵4<5<9,
∴2<<3,
∴﹣3<<﹣2,
∴﹣3<<﹣2.
故选:B.
8.D
解:A、,故不是最简二次根式,故错误;
B、,故错误;
C、,故错误;
D、,故与最接近的整数是3,故正确;
故选:D.
9.B
解:
A选项,,不符合题意;
B选项,,符合题意;
C选项,,不符合题意;
D选项,,不符合题意.
故选B.
10.C
解:分母有理化,可得a=2+,b=2-,
∴a-b=(2+)-(2-)=2,故A选项错误,不符合题意;
a+b=(2+)+(2-)=4,故B选项错误,不符合题意;
ab=(2+)×(2-)=4-3=1,故C选项正确,符合题意;
∵a2=(2+)2=4+4+3=7+4,b2=(2-)2=4-4+3=7-4,
∴a2≠b2,故D选项错误,不符合题意;
故选:C.
11.C
解:∵0<x<1,
∴设,
则;
;
;
∵,
∴;
故选:C.
12.C
解:∵,,,
∴,
∴的面积,
故选:C.
13.
解:∵,
∴,
∴;
故答案为:.
14.
解:∵,且a、b是两个连续的整数
∴
∴a=2,b=3,
∴==
故答案为:.
15.2a+2c
解:∵a,b,c是△ABC的三边的长,
∴a+c>b,a+b+c>0,
∴b﹣a﹣c<0,
∴+|b﹣a﹣c|=|a+b+c|+|b﹣a﹣c|=a+b+c+a+c-b=2a+2c.
故答案是:2a+2c.
16.
解:∵9<13<16,
∴,
∴,
∴,
∴x=2,y=,
∴==,
故答案为:.
17.
解:根据题中的新定义得:3☆10=,
则8☆(3☆10)=8☆6=
故答案为:.
18.2-+
解:∵正方形ABCD面积为2,
∴边长AB=AD=,对角线BD=2,
由作图可知:BE=BD=2,
∵点A所表示的数为,即OA=,
∴OB=OA-AB=-,
∴OE=BE-OB=2-(-)=2-+,
∴点E表示的数为2-+,
故答案为:2-+.
19.2+2
解:∵DE垂直平分AB,∠B=∠C=30°,
∴BE=AE,∠B=∠BAE=30°,
∴∠CAE=180°-∠B-∠BAE-∠C
=90°,
在Rt△CAE中,∠C=30°,
∴EC=2AE,
∴AE+EC=BE+EC=BC=2,即3AE=2,
∴AE=,EC=,
∴AC=,
∴∴△ACE的周长=AC+AE+CE=AC+BC=2+2,
故答案为:2+2.
20.
解:∵正方形ABCD的面积为7,正方形BEFG的面积为5,
∴BG=BE=,AB=BC=,
∴AG=AB-BG=-,
∴S△AGC=?AG?BC==,
故答案为:.
21.(1)2;(2)9
(1)解:
(2)
=
=9.
22..
解:原式,
,
,
将代入得:原式.
23.(1);(2)能,见解析
解:(1)设斜边上的高为h,
根据勾股定理:AB2=AC2+BC2;
∴,;
∴.
解得;
(2)能,作图如下:
24.
解:∵两张正方形纸片的面积分别为和,
∴它们的边长分别为,.
∴,
∴空白部分的周长.
25.(1);(2);(3)
解:(1)观察,如的下标3,与中被开方数,5和7得出:3×2-1=5,3×2+1=7,即7等于下标的2倍加1,5等于下标的2倍减1;
,
故答案是:;
(2)由(1)知,第n个等式的下标是n,被开方数分别为2n+1,2n-1,所以第n个等式
,
故答案是:;
(3)
.
26.(1);(2),
解:(1)由勾股定理及题意得:
;
(2)∵b=6,c=2,
∴,
∴,
∵,
∴.
27.(1);(2)见解析;(3)
解:(1)由题意可知
∵,
∴
,
∵为等腰直角三角形,
∴,
∴,
∵也是等腰直角三角形,
∴,,
∴,
∴,
∵,
∴,
作交于点,
∵,
∴,
∴,
∴;
(2)∵,,,
∴,
∴,
∴,
∴,
如图,设
则
∵
;
(3)由(2)可知,
,
∴,
当重合时,时,最小,此时重合,
∵且,
∴此时为的中点,
∵,
∴
.
