1.4.2 用空间向量研究距离、夹角问题 同步提升训练小卷(Word含答案解析)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题 同步提升训练小卷(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 879.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 14:15:27 | ||
图片预览




文档简介
2021-2022学年高二数学(人教A版2019选择性必修一)
1.2
空间向量基本定理
一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.设向量不共面,则下列可作为空间的一个基底的是( )
A.
B.
C.
D.
2.下列说法正确的是(
)
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底中基向量与基底基向量对应相等
3.在正方体中,可以作为空间向量的一组基底的是(
)
A.
B.
C.
D.
4.若为空间的一组基底,则下列各项中能构成基底的一组向量是(
)
A.
B.
C.
D.
5.已知空间四边形,其对角线、,、分别是边、的中点,点在线段上,且使,用向量,表示向量
是
A.
B.
C.
D.
6.给出下列命题:
①已知,则;
②、、、为空间四点,若、、不构成空间的一个基底,那么、、、共面;
③已知,则、与任何向量都不构成空间的一个基底;
④若、共线,则、所在直线或者平行或者重合.
正确的结论的个数为(
)
A.1
B.2
C.3
D.4
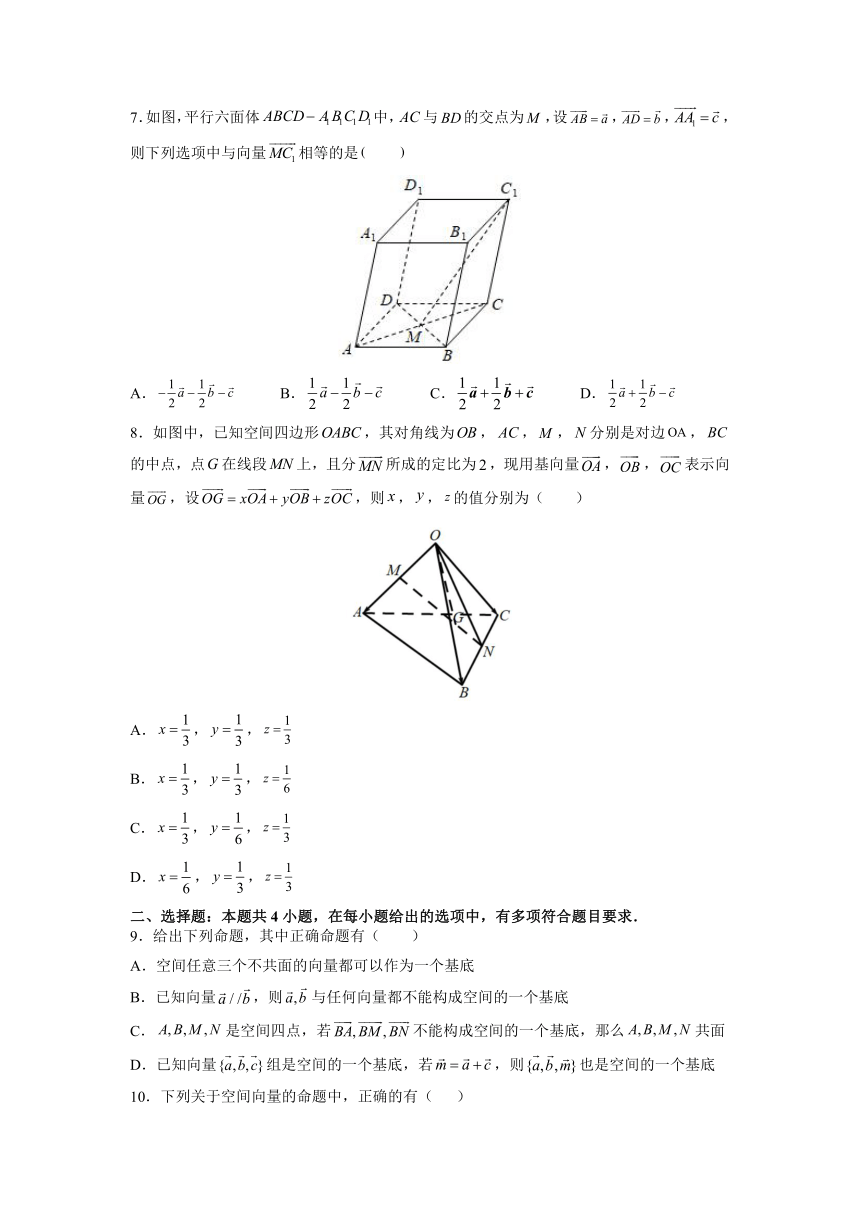
7.如图,平行六面体中,与的交点为,设,,,则下列选项中与向量相等的是
A.
B.
C.
D.
8.如图中,已知空间四边形,其对角线为,,,分别是对边,的中点,点在线段上,且分所成的定比为,现用基向量,,表示向量,设,则,,的值分别为(
)
A.,,
B.,,
C.,,
D.,,
二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求.
9.给出下列命题,其中正确命题有(
)
A.空间任意三个不共面的向量都可以作为一个基底
B.已知向量,则与任何向量都不能构成空间的一个基底
C.是空间四点,若不能构成空间的一个基底,那么共面
D.已知向量组是空间的一个基底,若,则也是空间的一个基底
10.下列关于空间向量的命题中,正确的有(
)
A.若向量,与空间任意向量都不能构成基底,则;
B.若非零向量,,满足,,则有;
C.若,,是空间的一组基底,且,则,,,四点共面;
D.若向量,,,是空间一组基底,则,,也是空间的一组基底.
11.(多选题)给出下列命题,其中正确命题有(?
?)
A.空间任意三个不共面的向量都可以作为一个基底
B.已知向量,则与任何向量都不能构成空间的一个基底
C.、、、为空间四点,若不构成空间的一个基底,则、、、共面;
D.已知是空间的一个基底,则基向量可以与向量构成空间另一个基底.
12.(多选题)在四面体中,以上说法正确的有(
)
A.若,则可知
B.若为△的重心,则
C.若,,则
D.若四面体各棱长都为2,分别为的中点,则
三、填空题:本题共4小题.
13.设且是空间的一组基底,给出下列向量组:
①;②
③
④
其中可以作为空间的基底的向量组是___________(填序号).
14..在四面体中,、分别是、的中点,若记,,,则______.
15.在正四面体中,,分别为棱、的中点,设,,,用,,表示向量__,异面直线与所成角的余弦值为__.
16.若,,,,若不共面,当时,α+β+γ=____.
四、解答题:本题共6小题.解答应写出文字说明、证明过程或演算步骤.
17.如图,已知正方体ABCD-A'B'C'D',点E是上底面A'B'C'D'的中心,取向量为基底的基向量,在下列条件下,分别求x,y,z的值.
(1)=x+y+z;
(2)=x+y+z.
18.若是空间的一个基底,试判断能否作为空间的一个基底.
19.已知,,为空间的一个基底,且,,,能否以作为空间的一组基底?若能,试以此基底表示向量;若不能,请说明理由.
20.如图,分别是四面体的棱的中点,是的三等分点.
(1)用向量
,,表示和.
(2)若四面体的所有棱长都等于1,求的值.
21.棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别是DD1,DB的中点,G在棱CD上,且CGCD.
(1)证明:EF⊥B1C;
(2)求cos,.
22.如图,三棱柱中,底面边长和侧棱长都等于1,.
(1)设,,,用向量,,表示,并求出的长度;
(2)求异面直线与所成角的余弦值.
参考答案
1.C
【解析】选项A,B中的三个向量都是共面向量,所以不能作为空间的一个基底.
选项D中,,根据空间向量共面定理得这三个向量共面,
所以不能作为空间的一个基底.
选项C中不共面,故可作为空间的一个基底.
故选:C.
2.C
【解析】项中应是不共面的三个向量构成空间向量的基底,
所以错.
项,空间基底有无数个,
所以错.
项中因为基底不唯一,所以错.
故选.
3.C
【解析】:
共面,排除A
共面,排除B
共面,排除D
三个向量是不共面的,可以作为一个基底.
故选:C
4.C
【解析】A:因为,所以向量是共面向量,
因此这三个向量不能构成基底;
B:因为,
所以向量是共面向量,因此这三个向量不能构成基底;
C:因为为空间的一组基底,所以这三个向量不共面.
若不构成一组基底,
则有,
所以向量是共面向量,这与这三个向量不共面矛盾,
故假设不正确,因此能构成一组基底,
D:因为,
所以向量是共面向量,
因此不能构成一组基底.
故选:C.
5.C
【解析】解:
故选:.
6.C
【解析】对于①,若,则,故,故①正确;
对于②,若、、不构成空间的一个基底,则、、这个向量在同一平面内,故、、、共面,故②正确;
对于③,当时,若与、不共面,则、、可构成空间的一个基底,故③不正确;
对于④,根据向量共线的定义可得其成立,故④正确,
故选:C.
7.C
【解析】解:平行六面体中,与的交点为,
设,,,
.
故选:C.
8.D
【解析】解:,分别是对边,的中点,
,.
点在线段上,且分所成的定比为,
.
.
即,,.
故选:D.
9.ABCD
【解析】选项中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以正确;
选项中,根据空间基底的概念,可得正确;
选项中,由不能构成空间的一个基底,可得共面,又由过相同点B,可得四点共面,所以正确;
选项中:由是空间的一个基底,则基向量与向量一定不共面,所以可以构成空间另一个基底,所以正确.
故选:ABCD.
10.ACD
【解析】解:对于A:若向量,与空间任意向量都不能构成基底,只能两个向量为共线向量,即,故A正确;
对于B:若非零向量,,满足,,则与不一定共线,故B错误;
对于C:若,,是空间的一组基底,且,
则,即,
可得到,,,四点共面,故C正确;
对于D:若向量,,,是空间一组基底,
则空间任意一个向量,存在唯一实数组,
使,
则,,也是空间的一组基底.
故选:ACD.
11.ABCD
【解析】解:选项中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以正确;选项中,根据空间基底的概念,可得正确;
选项中,、、、为空间四点,若不构成空间的一个基底,由空间共面向量定理可知:则必然共面,因此、、、共面,所以正确;
选项中:由是空间的一个基底,则基向量与向量一定不共面,所以可以构成空间另一个基底,所以正确.
故选:ABCD.
12.ABC
【解析】
对于
,,,
,
,即,故正确;
对于,为△的重心,则,,
即,故正确;
对于,若,,则,
,
,
,
,,故正确;
对于,
,故错误.
故选:ABC
13.②③④
【解析】如图,平行六面体中,设,
则,,因四点共面,则向量共面,
而四点不共面,则向量不共面,又四点不共面,则不共面,
四点不共面,则也不共面,
所以可以作为空间的基底的向量组是②③④.
故答案为:②③④
14.
【解析】解:四面体中,、分别是、的中点,则
故答案为:
15.
【解析】解:如图,
为棱的中点,,
;
又为棱的中点,,且的两两夹角都为,并设,
,
又,
,
异面直线与所成角的余弦值为.
故答案为:;.
16.3
【解析】由已知,
所以故有α+β+γ=3.
故答案为3
17.(1)x=1,y=-1,z=1;(2)x=,y=,z=1.
【解析】(1)因为=-,
又=x+y+z,
所以x=1,y=-1,z=1.
(2)因为=)
=,
又=x+y+z,
所以x=,y=,z=1.
18.能
【解析】假设,,共面,则存在实数λ,μ,使得=λ()+μ(),即=μ+λ+(λ+μ)
∵是空间的一个基底
∴,,不共面
∴此方程组无解
即不存在实数λ,μ,使得=λ()+μ()
∴,,不共面
故能作为空间的一个基底
19.能,.
【解析】解:假设存在不全为0的实数,,使得成立,
则,此方程组无解,
即不存在不全为0的实数,,使得成立,
因此假设不成立.
因此能以作为空间的一组基底.
设则有
因为,,为空间的一个基底,所以解得
故
20.(1),(2).
【解析】解:(1),
∴
(2)四面体的所有棱长都等于1,各面为等边三角形,
,,
21.(1)证明见解析
(2)
【解析】分别以三直线DA,DC,DD1为x,y,z轴,建立如图所示的空间直角坐标系,
则:E(0,0,1),F(1,1,0),B1(2,2,2),C(0,2,0),C1(0,2,2),
(1)证明:∵,
∴,
∴,
∴EF⊥B1C;
(2)∵,
∴,
∴,
∴,,
∴.
22.(1);;(2).
【解析】(1),
因为,同理可得,
所以.
(2)因为,所以,
因为,
所以.
所以异面直线与所成角的余弦值为.
1.2
空间向量基本定理
一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.设向量不共面,则下列可作为空间的一个基底的是( )
A.
B.
C.
D.
2.下列说法正确的是(
)
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底中基向量与基底基向量对应相等
3.在正方体中,可以作为空间向量的一组基底的是(
)
A.
B.
C.
D.
4.若为空间的一组基底,则下列各项中能构成基底的一组向量是(
)
A.
B.
C.
D.
5.已知空间四边形,其对角线、,、分别是边、的中点,点在线段上,且使,用向量,表示向量
是
A.
B.
C.
D.
6.给出下列命题:
①已知,则;
②、、、为空间四点,若、、不构成空间的一个基底,那么、、、共面;
③已知,则、与任何向量都不构成空间的一个基底;
④若、共线,则、所在直线或者平行或者重合.
正确的结论的个数为(
)
A.1
B.2
C.3
D.4
7.如图,平行六面体中,与的交点为,设,,,则下列选项中与向量相等的是
A.
B.
C.
D.
8.如图中,已知空间四边形,其对角线为,,,分别是对边,的中点,点在线段上,且分所成的定比为,现用基向量,,表示向量,设,则,,的值分别为(
)
A.,,
B.,,
C.,,
D.,,
二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求.
9.给出下列命题,其中正确命题有(
)
A.空间任意三个不共面的向量都可以作为一个基底
B.已知向量,则与任何向量都不能构成空间的一个基底
C.是空间四点,若不能构成空间的一个基底,那么共面
D.已知向量组是空间的一个基底,若,则也是空间的一个基底
10.下列关于空间向量的命题中,正确的有(
)
A.若向量,与空间任意向量都不能构成基底,则;
B.若非零向量,,满足,,则有;
C.若,,是空间的一组基底,且,则,,,四点共面;
D.若向量,,,是空间一组基底,则,,也是空间的一组基底.
11.(多选题)给出下列命题,其中正确命题有(?
?)
A.空间任意三个不共面的向量都可以作为一个基底
B.已知向量,则与任何向量都不能构成空间的一个基底
C.、、、为空间四点,若不构成空间的一个基底,则、、、共面;
D.已知是空间的一个基底,则基向量可以与向量构成空间另一个基底.
12.(多选题)在四面体中,以上说法正确的有(
)
A.若,则可知
B.若为△的重心,则
C.若,,则
D.若四面体各棱长都为2,分别为的中点,则
三、填空题:本题共4小题.
13.设且是空间的一组基底,给出下列向量组:
①;②
③
④
其中可以作为空间的基底的向量组是___________(填序号).
14..在四面体中,、分别是、的中点,若记,,,则______.
15.在正四面体中,,分别为棱、的中点,设,,,用,,表示向量__,异面直线与所成角的余弦值为__.
16.若,,,,若不共面,当时,α+β+γ=____.
四、解答题:本题共6小题.解答应写出文字说明、证明过程或演算步骤.
17.如图,已知正方体ABCD-A'B'C'D',点E是上底面A'B'C'D'的中心,取向量为基底的基向量,在下列条件下,分别求x,y,z的值.
(1)=x+y+z;
(2)=x+y+z.
18.若是空间的一个基底,试判断能否作为空间的一个基底.
19.已知,,为空间的一个基底,且,,,能否以作为空间的一组基底?若能,试以此基底表示向量;若不能,请说明理由.
20.如图,分别是四面体的棱的中点,是的三等分点.
(1)用向量
,,表示和.
(2)若四面体的所有棱长都等于1,求的值.
21.棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别是DD1,DB的中点,G在棱CD上,且CGCD.
(1)证明:EF⊥B1C;
(2)求cos,.
22.如图,三棱柱中,底面边长和侧棱长都等于1,.
(1)设,,,用向量,,表示,并求出的长度;
(2)求异面直线与所成角的余弦值.
参考答案
1.C
【解析】选项A,B中的三个向量都是共面向量,所以不能作为空间的一个基底.
选项D中,,根据空间向量共面定理得这三个向量共面,
所以不能作为空间的一个基底.
选项C中不共面,故可作为空间的一个基底.
故选:C.
2.C
【解析】项中应是不共面的三个向量构成空间向量的基底,
所以错.
项,空间基底有无数个,
所以错.
项中因为基底不唯一,所以错.
故选.
3.C
【解析】:
共面,排除A
共面,排除B
共面,排除D
三个向量是不共面的,可以作为一个基底.
故选:C
4.C
【解析】A:因为,所以向量是共面向量,
因此这三个向量不能构成基底;
B:因为,
所以向量是共面向量,因此这三个向量不能构成基底;
C:因为为空间的一组基底,所以这三个向量不共面.
若不构成一组基底,
则有,
所以向量是共面向量,这与这三个向量不共面矛盾,
故假设不正确,因此能构成一组基底,
D:因为,
所以向量是共面向量,
因此不能构成一组基底.
故选:C.
5.C
【解析】解:
故选:.
6.C
【解析】对于①,若,则,故,故①正确;
对于②,若、、不构成空间的一个基底,则、、这个向量在同一平面内,故、、、共面,故②正确;
对于③,当时,若与、不共面,则、、可构成空间的一个基底,故③不正确;
对于④,根据向量共线的定义可得其成立,故④正确,
故选:C.
7.C
【解析】解:平行六面体中,与的交点为,
设,,,
.
故选:C.
8.D
【解析】解:,分别是对边,的中点,
,.
点在线段上,且分所成的定比为,
.
.
即,,.
故选:D.
9.ABCD
【解析】选项中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以正确;
选项中,根据空间基底的概念,可得正确;
选项中,由不能构成空间的一个基底,可得共面,又由过相同点B,可得四点共面,所以正确;
选项中:由是空间的一个基底,则基向量与向量一定不共面,所以可以构成空间另一个基底,所以正确.
故选:ABCD.
10.ACD
【解析】解:对于A:若向量,与空间任意向量都不能构成基底,只能两个向量为共线向量,即,故A正确;
对于B:若非零向量,,满足,,则与不一定共线,故B错误;
对于C:若,,是空间的一组基底,且,
则,即,
可得到,,,四点共面,故C正确;
对于D:若向量,,,是空间一组基底,
则空间任意一个向量,存在唯一实数组,
使,
则,,也是空间的一组基底.
故选:ACD.
11.ABCD
【解析】解:选项中,根据空间基底的概念,可得任意三个不共面的向量都可以作为一个空间基底,所以正确;选项中,根据空间基底的概念,可得正确;
选项中,、、、为空间四点,若不构成空间的一个基底,由空间共面向量定理可知:则必然共面,因此、、、共面,所以正确;
选项中:由是空间的一个基底,则基向量与向量一定不共面,所以可以构成空间另一个基底,所以正确.
故选:ABCD.
12.ABC
【解析】
对于
,,,
,
,即,故正确;
对于,为△的重心,则,,
即,故正确;
对于,若,,则,
,
,
,
,,故正确;
对于,
,故错误.
故选:ABC
13.②③④
【解析】如图,平行六面体中,设,
则,,因四点共面,则向量共面,
而四点不共面,则向量不共面,又四点不共面,则不共面,
四点不共面,则也不共面,
所以可以作为空间的基底的向量组是②③④.
故答案为:②③④
14.
【解析】解:四面体中,、分别是、的中点,则
故答案为:
15.
【解析】解:如图,
为棱的中点,,
;
又为棱的中点,,且的两两夹角都为,并设,
,
又,
,
异面直线与所成角的余弦值为.
故答案为:;.
16.3
【解析】由已知,
所以故有α+β+γ=3.
故答案为3
17.(1)x=1,y=-1,z=1;(2)x=,y=,z=1.
【解析】(1)因为=-,
又=x+y+z,
所以x=1,y=-1,z=1.
(2)因为=)
=,
又=x+y+z,
所以x=,y=,z=1.
18.能
【解析】假设,,共面,则存在实数λ,μ,使得=λ()+μ(),即=μ+λ+(λ+μ)
∵是空间的一个基底
∴,,不共面
∴此方程组无解
即不存在实数λ,μ,使得=λ()+μ()
∴,,不共面
故能作为空间的一个基底
19.能,.
【解析】解:假设存在不全为0的实数,,使得成立,
则,此方程组无解,
即不存在不全为0的实数,,使得成立,
因此假设不成立.
因此能以作为空间的一组基底.
设则有
因为,,为空间的一个基底,所以解得
故
20.(1),(2).
【解析】解:(1),
∴
(2)四面体的所有棱长都等于1,各面为等边三角形,
,,
21.(1)证明见解析
(2)
【解析】分别以三直线DA,DC,DD1为x,y,z轴,建立如图所示的空间直角坐标系,
则:E(0,0,1),F(1,1,0),B1(2,2,2),C(0,2,0),C1(0,2,2),
(1)证明:∵,
∴,
∴,
∴EF⊥B1C;
(2)∵,
∴,
∴,
∴,,
∴.
22.(1);;(2).
【解析】(1),
因为,同理可得,
所以.
(2)因为,所以,
因为,
所以.
所以异面直线与所成角的余弦值为.
