1.4.2 用空间向量研究距离、夹角问题 同步提升训练小卷 - 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题 同步提升训练小卷 - 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 14:16:33 | ||
图片预览



文档简介
2021-2022学年高二数学(人教A版2019选择性必修一)
1.4.2
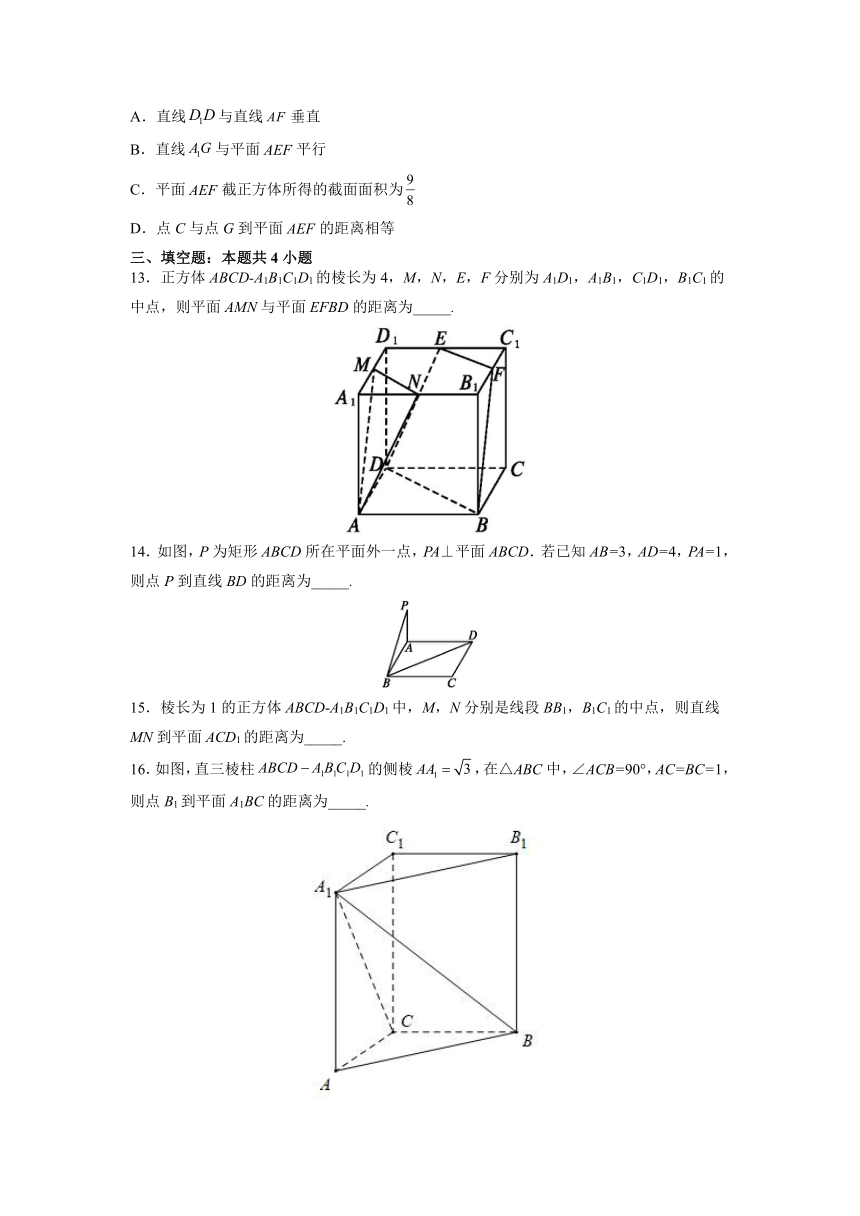
用空间向量研究距离、夹角问题
一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.若点A(2,3,2)关于xoz平面的对称点为A',点B(﹣2,1,4),关于y轴对称点为B',点M为线段A'B'的中点,则|MA|=(
)
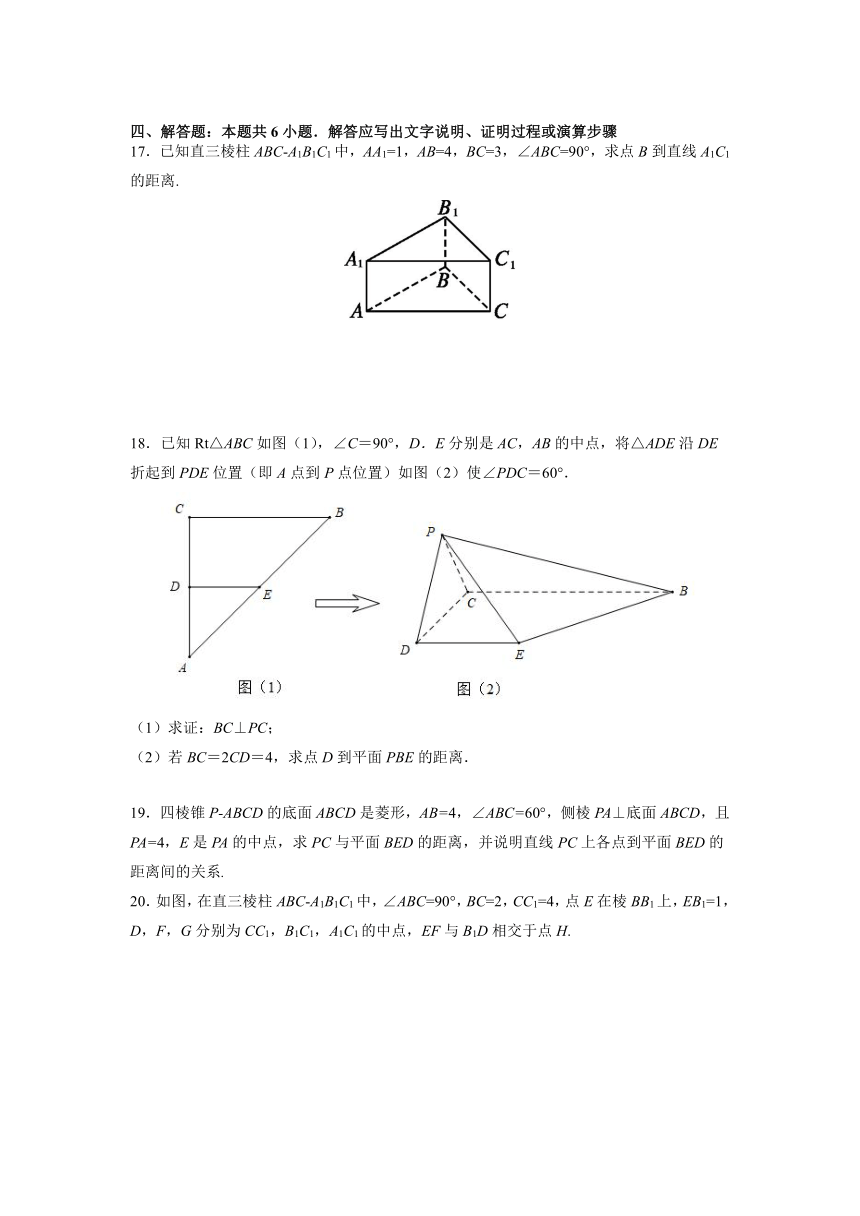
A.
B.
C.5
D.
2.在棱长为的正方体中,是的中点,则点到平面的距离是( )
A.
B.
C.
D.
3.已知平面α的一个法向量n=(-2,-2,1),点A(-1,3,0)在α内,则P(-2,1,4)到α的距离为( )
A.10
B.3
C.
D.
4.若O为坐标原点,
=(1,1,-2),=(3,2,8),=(0,1,0),则线段AB的中点P到点C的距离为( )
A.
B.
C.
D.
5.正方体的棱长为1,动点在线段上,动点在平面上,且平面.线段长度的取值范围为(
)
A.
B.
C.
D.
6.如图,已知正方形的边长为
,分别是
的中点,⊥平面
,且,则点
到平面的距离为
A.
B.
C.
D.1
7.若三棱锥P-ABC的三条侧棱两两垂直,且满足PA=PB=PC=1,则点P到平面ABC的距离是(
)
A.
B.
C.
D.
8.如图,棱长为1的正方体,是底面的中心,则到平面的距离是(
)
A.
B.
C.
D.
二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求
9.在正方体中,分别是和的中点,则下列结论正确的是(
)
A.//平面
B.平面
C.
D.点与点到平面的距离相等
10.如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.三棱锥P﹣A1C1D的体积为定值
C.异面直线AP与A1D所成角的取值范用是[45°,90°]
D.直线C1P与平面A1C1D所成角的正弦值的最大值为
11.正方体中,下列叙述正确的有( )
A.直线与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面所成角为
12.如图,正方体的棱长为1,分别为的中点.则(
)
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截面面积为
D.点C与点G到平面的距离相等
三、填空题:本题共4小题
13.正方体ABCD-A1B1C1D1的棱长为4,M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,则平面AMN与平面EFBD的距离为_____.?
14.如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD.若已知AB=3,AD=4,PA=1,则点P到直线BD的距离为_____.?
15.棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的中点,则直线MN到平面ACD1的距离为_____.
16.如图,直三棱柱的侧棱,在△ABC中,∠ACB=90°,AC=BC=1,则点B1到平面A1BC的距离为_____.
四、解答题:本题共6小题.解答应写出文字说明、证明过程或演算步骤
17.已知直三棱柱ABC-A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,求点B到直线A1C1的距离.
18.已知Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
(1)求证:BC⊥PC;
(2)若BC=2CD=4,求点D到平面PBE的距离.
19.四棱锥P-ABCD的底面ABCD是菱形,AB=4,∠ABC=60°,侧棱PA⊥底面ABCD,且PA=4,E是PA的中点,求PC与平面BED的距离,并说明直线PC上各点到平面BED的距离间的关系.
20.如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在棱BB1上,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
(1)求证:B1D⊥平面ABD;
(2)求证:平面EGF∥平面ABD;
(3)求平面EGF与平面ABD的距离.
21.在直三棱柱中,,,是的中点.
(1)求证:平面;
(2)求直线到平面的距离.
22.在三棱锥中,是边长为的正三角形,平面平面,,,分别为,的中点,如图所示.求点到平面的距离.
参考答案
1.C
【解析】∵点A(2,3,2)关于xoz平面的对称点为A',
∴A′(2,﹣3,2),
∵点B(﹣2,1,4)关于y轴对称点为B',
∴B′(2,1,﹣4),
∵点M为线段A'B'的中点,∴M(2,﹣1,﹣1),
∴|MA|==5.
故选:C.
2.A
【解析】以为空间直角坐标原点,分别为轴建立空间直角坐标系.由于是中点,故,且,设是平面的法向量,故,故可设,故到平面的距离.故选A.
3.D
【解析】=(1,2,-4),又平面α的一个法向量为n=(-2,-2,1),
所以P到α的距离为=.
故答案为D
4.D
【解析】由题意=
(+)=,=-=,||=.
故答案为D
5.D
【解析】以分别为建立空间直角坐标系,
则,
,,
由平面,则且
所以得
所以
当时,,当或时,,
所以
故选:D
6.B
【解析】以C为原点CD为x轴CB为y轴CG为z轴建立空间坐标系,所以平面的一个法向量为
7.D
【解析】解:分别以PA,PB,PC所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则A(1,0,0),B(0,1,0),C(0,0,1)..
设平面ABC的一个法向量为,由得:.
令,则.则平面ABC的一个法向量为.所以点P到平面ABC的距离.
故选:.
8.B
【解析】
如图建立空间直角坐标系,则:
由于平面平面
,又,
平面
故平面的一个法向量为:
到平面的距离为:
故选:B
9.AC
【解析】对A,因为分别是和的中点
故,故//平面成立.
对B,建立如图空间直角坐标系,
设正方体边长为2
则,.故.
故不互相垂直.又属于平面.故平面不成立.
对C,
,.
,故成立.
对D,点与点到平面的距离相等则点与点中点在平面上.
连接易得平面即平面.
又点与点中点在上,故点不在平面上.故D不成立.
故选:AC
10.ABD
【解析】解:在A中,∵A1C1⊥B1D1,A1C1⊥BB1,B1D1∩BB1=B1,
∴A1C1⊥平面BB1D1,∴A1C1⊥BD1,同理,DC1⊥BD1,
∵A1C1∩DC1=C1,∴直线BD1⊥平面A1C1D,故A正确;
在B中,∵A1D∥B1C,A1D?平面A1C1D,B1C?平面A1C1D,
∴B1C∥平面
A1C1D,
∵点P在线段B1C上运动,∴P到平面A1C1D的距离为定值,
又△A1C1D的面积是定值,∴三棱锥P﹣A1C1D的体积为定值,故B正确;
在C中,异面直线AP与A1D所成角的取值范用是[60°,90°],故C错误;
在D中,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD﹣A1B1C1D1中棱长为1,P(a,1,a),
则D(0,0,0),A1(1,0,1),C1(0,1,1),=(1,0,1),=(0,1,1),=(a,0,a﹣1),
设平面A1C1D的法向量,
则,取x=1,得,
∴直线C1P与平面A1C1D所成角的正弦值为:
==,
∴当a=时,直线C1P与平面A1C1D所成角的正弦值的最大值为,故D正确.
故选:ABD.
11.AB
【解析】设正方体的棱长为,以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、、、,
所以,,,,,
对于A选项,,
所以,直线与所成角为,A对;
对于B选项,,即,
所以,直线与所成角为,B对;
对于C选项,平面的一个法向量为,,
所以,直线与平面所成角不是,C错;
对于D选项,平面的一个法向量为,
,
所以,直线与平面所成角为,D错.
故选:AB.
12.BC
【解析】对于A:在正方体中,,因为直线与直线不垂直,所以直线与直线不垂直.故A错误;
对于B:
取的中点N,连结GN,A1N,因为,N分别为,的中点,所以由三角形中位线定理得:所以
因为面,EF面,所以面.
同理可证:面.
又面,面,,
所以面面,所以直线与平面平行.故B正确;
对于C:连结,由上面证明过程可知,所以平面截正方体所得的截面为面.因为,
,
所以为等腰梯形,如图示:
过E、F分别作EP、FQ垂直AD1于P、Q,则,
所以,
所以等腰梯形的面积为.
故C正确.
对于D:假设C与G到平面AEF的距离相等,即平面AEF将CG平分,则平面AEF必过CG的中点,连接CG交EF于H,而H不是CG中点,则假设不成立,故D错误.
故选:BC
13.
【解析】如图所示,建立空间直角坐标系Dxyz,
则A(4,0,0),M(2,0,4),D(0,0,0),B(4,4,0),E(0,2,4),
F(2,4,4),N(4,2,4).
∴=(2,2,0),=(2,2,0),=(2,0,4),=(2,0,4),
∴,
∴EF∥MN,BF∥AM,EF∩BF=F,MN∩AM=M.
∴平面AMN∥平面EFBD.
设=(x,y,z)是平面AMN的一个法向量,
则解得
取z=1,则x=2,y=-2,得=(2,2,1).
平面AMN到平面EFBD的距离就是点B到平面EFBD的距离.
∵=(0,4,0),∴平面AMN与平面EFBD间的距离d=.
故答案为:
14.
【解析】如图,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,1),B(3,0,0),D(0,4,0),
则=(3,0,-1),=(-3,4,0),
故点P到直线BD的距离,
所以点P到直线BD的距离为.
故答案为:.
15.
【解析】解:如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
则D(0,0,0),C(0,1,0),D1(0,0,1),M,A(1,0,0).
∴=(-1,1,0),=(-1,0,1).
设平面的法向量为,
则即
令x=1,则y=z=1,∴.
∴点M到平面ACD1的距离.
又,故平面.故直线MN到平面ACD1的距离为.
故答案为:.
16.
【解析】如图所示,建立空间直角坐标系,
则A(1,0,0),B(0,1,0),C(0,0,0),,,
,
∴,,
设平面A1BC的法向量为
则,即令z=1得,y=0,
所以点B1到平面A1BC的距离.
故答案为:
17.
【解析】解:以B为坐标原点,建立如图所示的空间直角坐标系,则A1(4,0,1),C1(0,3,1).
直线A1C1的方向向量=(-4,3,0),=(0,3,1),所以点B到直线A1C1的距离.
18.(1)见解析;(2)
【解析】(1)证明:∵Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,
将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
∴DE⊥DC,DE⊥PD,DE∥BC,
∵PD∩DC=D,∴DE⊥平面PCD,∴BC⊥平面PCD,
∵PC?平面PCD,∴BC⊥PC.
(2)解:∵D.E分别是AC,AB的中点,∠PDC=60°,BC=2CD=4,
∴CD=PD=PC=2,
取CD中点O,BE中点M,连结PO,MO,则OP,OD,OM两两垂直,
以O为原点,OD为x轴,OM为y轴,OP为z轴,建立空间直角坐标系:
则D(1,0,0),P(0,0,),B(﹣1,4,0),E(1,2,0),
(1,0,),(﹣1,4,),(1,2,),
设平面PBE的法向量(x,y,z),
则,取x=1,得(1,1,),
∴点D到平面PBE的距离为:
d.
19.,相等.
【解析】以A为原点,AB所在直线为x轴,△ACD中CD边上的高AF所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,如图所示,
则F为CD的中点,A(0,0,0),B(4,0,0),F(0,2,0),C(2,2,0),
D(-2,2,0),P(0,0,4),E(0,0,2).
设平面BED的一个法向量为,
由
得即
取z=2,则x=1,,得
∵,∴,
∴⊥,故PC∥平面BED,
∴PC到平面BED的距离就是点P到平面BED的距离.
∵,∴点P到平面BED的距离,
即PC到平面BED的距离为,且直线PC上各点到平面BED的距离都相等.
20.(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】(1)证明:如图所示建立空间直角坐标系,
设AB=a,则A1(a,0,0),B1(0,0,0),C1(0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),B(0,0,4),
D(0,2,2),G.
所以=(0,2,2),=(-a,0,0),=(0,2,-2).
所以=0+0+0=0,=0+4-4=0.
所以,
所以B1D⊥AB,B1D⊥BD.
又AB∩BD=B,所以B1D⊥平面ABD.
(2)证明:由(1)可得=(-a,0,0),=(0,2,-2),=(0,1,-1),所以=2=2,所以.
所以GF∥AB,EF∥BD.
又GF∩EF=F,AB∩BD=B,所以平面EGF∥平面ABD.
(3)解:由(1)(2)知,是平面EGF和平面ABD的法向量.
因为平面EGF∥平面ABD,所以点E到平面ABD的距离就是两平面的距离,设为d.
因为=(0,0,3),=(0,2,2),
所以d=.即两平面间的距离为.
21.(1)证明见解析;(2).
【解析】(1)证明:连接交于点,连接,则点为中点,
又是的中点,所以,
因为平面,平面,
所以平面;
(2)解:因为平面,所以到平面的距离就等于点到平面的距离.
以点为坐标原点,建立如图所示的空间直角坐标系,
则,,,
,,.
设平面的法向量为,
所以,即,即
令,则.
所求距离为.
22.
【解析】取的中点,连接,.
∵,,∴,.
∵平面平面,平面平面,
∴平面.
又平面,∴.
如图所示,分别以,,所在直线为轴,轴,轴,
建立空间直角坐标系,则,,
,,.
∴,,.
设为平面的一个法向量,
则取,
则,,∴.
∴点到平面的距离.
1.4.2
用空间向量研究距离、夹角问题
一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.若点A(2,3,2)关于xoz平面的对称点为A',点B(﹣2,1,4),关于y轴对称点为B',点M为线段A'B'的中点,则|MA|=(
)
A.
B.
C.5
D.
2.在棱长为的正方体中,是的中点,则点到平面的距离是( )
A.
B.
C.
D.
3.已知平面α的一个法向量n=(-2,-2,1),点A(-1,3,0)在α内,则P(-2,1,4)到α的距离为( )
A.10
B.3
C.
D.
4.若O为坐标原点,
=(1,1,-2),=(3,2,8),=(0,1,0),则线段AB的中点P到点C的距离为( )
A.
B.
C.
D.
5.正方体的棱长为1,动点在线段上,动点在平面上,且平面.线段长度的取值范围为(
)
A.
B.
C.
D.
6.如图,已知正方形的边长为
,分别是
的中点,⊥平面
,且,则点
到平面的距离为
A.
B.
C.
D.1
7.若三棱锥P-ABC的三条侧棱两两垂直,且满足PA=PB=PC=1,则点P到平面ABC的距离是(
)
A.
B.
C.
D.
8.如图,棱长为1的正方体,是底面的中心,则到平面的距离是(
)
A.
B.
C.
D.
二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求
9.在正方体中,分别是和的中点,则下列结论正确的是(
)
A.//平面
B.平面
C.
D.点与点到平面的距离相等
10.如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则( )
A.直线BD1⊥平面A1C1D
B.三棱锥P﹣A1C1D的体积为定值
C.异面直线AP与A1D所成角的取值范用是[45°,90°]
D.直线C1P与平面A1C1D所成角的正弦值的最大值为
11.正方体中,下列叙述正确的有( )
A.直线与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面所成角为
12.如图,正方体的棱长为1,分别为的中点.则(
)
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截面面积为
D.点C与点G到平面的距离相等
三、填空题:本题共4小题
13.正方体ABCD-A1B1C1D1的棱长为4,M,N,E,F分别为A1D1,A1B1,C1D1,B1C1的中点,则平面AMN与平面EFBD的距离为_____.?
14.如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD.若已知AB=3,AD=4,PA=1,则点P到直线BD的距离为_____.?
15.棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的中点,则直线MN到平面ACD1的距离为_____.
16.如图,直三棱柱的侧棱,在△ABC中,∠ACB=90°,AC=BC=1,则点B1到平面A1BC的距离为_____.
四、解答题:本题共6小题.解答应写出文字说明、证明过程或演算步骤
17.已知直三棱柱ABC-A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,求点B到直线A1C1的距离.
18.已知Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
(1)求证:BC⊥PC;
(2)若BC=2CD=4,求点D到平面PBE的距离.
19.四棱锥P-ABCD的底面ABCD是菱形,AB=4,∠ABC=60°,侧棱PA⊥底面ABCD,且PA=4,E是PA的中点,求PC与平面BED的距离,并说明直线PC上各点到平面BED的距离间的关系.
20.如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在棱BB1上,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
(1)求证:B1D⊥平面ABD;
(2)求证:平面EGF∥平面ABD;
(3)求平面EGF与平面ABD的距离.
21.在直三棱柱中,,,是的中点.
(1)求证:平面;
(2)求直线到平面的距离.
22.在三棱锥中,是边长为的正三角形,平面平面,,,分别为,的中点,如图所示.求点到平面的距离.
参考答案
1.C
【解析】∵点A(2,3,2)关于xoz平面的对称点为A',
∴A′(2,﹣3,2),
∵点B(﹣2,1,4)关于y轴对称点为B',
∴B′(2,1,﹣4),
∵点M为线段A'B'的中点,∴M(2,﹣1,﹣1),
∴|MA|==5.
故选:C.
2.A
【解析】以为空间直角坐标原点,分别为轴建立空间直角坐标系.由于是中点,故,且,设是平面的法向量,故,故可设,故到平面的距离.故选A.
3.D
【解析】=(1,2,-4),又平面α的一个法向量为n=(-2,-2,1),
所以P到α的距离为=.
故答案为D
4.D
【解析】由题意=
(+)=,=-=,||=.
故答案为D
5.D
【解析】以分别为建立空间直角坐标系,
则,
,,
由平面,则且
所以得
所以
当时,,当或时,,
所以
故选:D
6.B
【解析】以C为原点CD为x轴CB为y轴CG为z轴建立空间坐标系,所以平面的一个法向量为
7.D
【解析】解:分别以PA,PB,PC所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则A(1,0,0),B(0,1,0),C(0,0,1)..
设平面ABC的一个法向量为,由得:.
令,则.则平面ABC的一个法向量为.所以点P到平面ABC的距离.
故选:.
8.B
【解析】
如图建立空间直角坐标系,则:
由于平面平面
,又,
平面
故平面的一个法向量为:
到平面的距离为:
故选:B
9.AC
【解析】对A,因为分别是和的中点
故,故//平面成立.
对B,建立如图空间直角坐标系,
设正方体边长为2
则,.故.
故不互相垂直.又属于平面.故平面不成立.
对C,
,.
,故成立.
对D,点与点到平面的距离相等则点与点中点在平面上.
连接易得平面即平面.
又点与点中点在上,故点不在平面上.故D不成立.
故选:AC
10.ABD
【解析】解:在A中,∵A1C1⊥B1D1,A1C1⊥BB1,B1D1∩BB1=B1,
∴A1C1⊥平面BB1D1,∴A1C1⊥BD1,同理,DC1⊥BD1,
∵A1C1∩DC1=C1,∴直线BD1⊥平面A1C1D,故A正确;
在B中,∵A1D∥B1C,A1D?平面A1C1D,B1C?平面A1C1D,
∴B1C∥平面
A1C1D,
∵点P在线段B1C上运动,∴P到平面A1C1D的距离为定值,
又△A1C1D的面积是定值,∴三棱锥P﹣A1C1D的体积为定值,故B正确;
在C中,异面直线AP与A1D所成角的取值范用是[60°,90°],故C错误;
在D中,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD﹣A1B1C1D1中棱长为1,P(a,1,a),
则D(0,0,0),A1(1,0,1),C1(0,1,1),=(1,0,1),=(0,1,1),=(a,0,a﹣1),
设平面A1C1D的法向量,
则,取x=1,得,
∴直线C1P与平面A1C1D所成角的正弦值为:
==,
∴当a=时,直线C1P与平面A1C1D所成角的正弦值的最大值为,故D正确.
故选:ABD.
11.AB
【解析】设正方体的棱长为,以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、、、,
所以,,,,,
对于A选项,,
所以,直线与所成角为,A对;
对于B选项,,即,
所以,直线与所成角为,B对;
对于C选项,平面的一个法向量为,,
所以,直线与平面所成角不是,C错;
对于D选项,平面的一个法向量为,
,
所以,直线与平面所成角为,D错.
故选:AB.
12.BC
【解析】对于A:在正方体中,,因为直线与直线不垂直,所以直线与直线不垂直.故A错误;
对于B:
取的中点N,连结GN,A1N,因为,N分别为,的中点,所以由三角形中位线定理得:所以
因为面,EF面,所以面.
同理可证:面.
又面,面,,
所以面面,所以直线与平面平行.故B正确;
对于C:连结,由上面证明过程可知,所以平面截正方体所得的截面为面.因为,
,
所以为等腰梯形,如图示:
过E、F分别作EP、FQ垂直AD1于P、Q,则,
所以,
所以等腰梯形的面积为.
故C正确.
对于D:假设C与G到平面AEF的距离相等,即平面AEF将CG平分,则平面AEF必过CG的中点,连接CG交EF于H,而H不是CG中点,则假设不成立,故D错误.
故选:BC
13.
【解析】如图所示,建立空间直角坐标系Dxyz,
则A(4,0,0),M(2,0,4),D(0,0,0),B(4,4,0),E(0,2,4),
F(2,4,4),N(4,2,4).
∴=(2,2,0),=(2,2,0),=(2,0,4),=(2,0,4),
∴,
∴EF∥MN,BF∥AM,EF∩BF=F,MN∩AM=M.
∴平面AMN∥平面EFBD.
设=(x,y,z)是平面AMN的一个法向量,
则解得
取z=1,则x=2,y=-2,得=(2,2,1).
平面AMN到平面EFBD的距离就是点B到平面EFBD的距离.
∵=(0,4,0),∴平面AMN与平面EFBD间的距离d=.
故答案为:
14.
【解析】如图,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,1),B(3,0,0),D(0,4,0),
则=(3,0,-1),=(-3,4,0),
故点P到直线BD的距离,
所以点P到直线BD的距离为.
故答案为:.
15.
【解析】解:如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
则D(0,0,0),C(0,1,0),D1(0,0,1),M,A(1,0,0).
∴=(-1,1,0),=(-1,0,1).
设平面的法向量为,
则即
令x=1,则y=z=1,∴.
∴点M到平面ACD1的距离.
又,故平面.故直线MN到平面ACD1的距离为.
故答案为:.
16.
【解析】如图所示,建立空间直角坐标系,
则A(1,0,0),B(0,1,0),C(0,0,0),,,
,
∴,,
设平面A1BC的法向量为
则,即令z=1得,y=0,
所以点B1到平面A1BC的距离.
故答案为:
17.
【解析】解:以B为坐标原点,建立如图所示的空间直角坐标系,则A1(4,0,1),C1(0,3,1).
直线A1C1的方向向量=(-4,3,0),=(0,3,1),所以点B到直线A1C1的距离.
18.(1)见解析;(2)
【解析】(1)证明:∵Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,
将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
∴DE⊥DC,DE⊥PD,DE∥BC,
∵PD∩DC=D,∴DE⊥平面PCD,∴BC⊥平面PCD,
∵PC?平面PCD,∴BC⊥PC.
(2)解:∵D.E分别是AC,AB的中点,∠PDC=60°,BC=2CD=4,
∴CD=PD=PC=2,
取CD中点O,BE中点M,连结PO,MO,则OP,OD,OM两两垂直,
以O为原点,OD为x轴,OM为y轴,OP为z轴,建立空间直角坐标系:
则D(1,0,0),P(0,0,),B(﹣1,4,0),E(1,2,0),
(1,0,),(﹣1,4,),(1,2,),
设平面PBE的法向量(x,y,z),
则,取x=1,得(1,1,),
∴点D到平面PBE的距离为:
d.
19.,相等.
【解析】以A为原点,AB所在直线为x轴,△ACD中CD边上的高AF所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,如图所示,
则F为CD的中点,A(0,0,0),B(4,0,0),F(0,2,0),C(2,2,0),
D(-2,2,0),P(0,0,4),E(0,0,2).
设平面BED的一个法向量为,
由
得即
取z=2,则x=1,,得
∵,∴,
∴⊥,故PC∥平面BED,
∴PC到平面BED的距离就是点P到平面BED的距离.
∵,∴点P到平面BED的距离,
即PC到平面BED的距离为,且直线PC上各点到平面BED的距离都相等.
20.(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】(1)证明:如图所示建立空间直角坐标系,
设AB=a,则A1(a,0,0),B1(0,0,0),C1(0,2,0),F(0,1,0),E(0,0,1),A(a,0,4),B(0,0,4),
D(0,2,2),G.
所以=(0,2,2),=(-a,0,0),=(0,2,-2).
所以=0+0+0=0,=0+4-4=0.
所以,
所以B1D⊥AB,B1D⊥BD.
又AB∩BD=B,所以B1D⊥平面ABD.
(2)证明:由(1)可得=(-a,0,0),=(0,2,-2),=(0,1,-1),所以=2=2,所以.
所以GF∥AB,EF∥BD.
又GF∩EF=F,AB∩BD=B,所以平面EGF∥平面ABD.
(3)解:由(1)(2)知,是平面EGF和平面ABD的法向量.
因为平面EGF∥平面ABD,所以点E到平面ABD的距离就是两平面的距离,设为d.
因为=(0,0,3),=(0,2,2),
所以d=.即两平面间的距离为.
21.(1)证明见解析;(2).
【解析】(1)证明:连接交于点,连接,则点为中点,
又是的中点,所以,
因为平面,平面,
所以平面;
(2)解:因为平面,所以到平面的距离就等于点到平面的距离.
以点为坐标原点,建立如图所示的空间直角坐标系,
则,,,
,,.
设平面的法向量为,
所以,即,即
令,则.
所求距离为.
22.
【解析】取的中点,连接,.
∵,,∴,.
∵平面平面,平面平面,
∴平面.
又平面,∴.
如图所示,分别以,,所在直线为轴,轴,轴,
建立空间直角坐标系,则,,
,,.
∴,,.
设为平面的一个法向量,
则取,
则,,∴.
∴点到平面的距离.
