人教B版(2019)必修 第一册一元二次不等式及其解法课件(共17张PPT)
文档属性
| 名称 | 人教B版(2019)必修 第一册一元二次不等式及其解法课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 730.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 13:23:07 | ||
图片预览




文档简介
(共17张PPT)
3.2
一元二次不等式及其解法
=
=
<
<
>
>
一元一次不等式可用图象法求解
练习1.求方程
的根?
复习:一元一次不等式的解法
今年的植树节我校高一年级的同学去植树时遇到一个这样的问题,我们准备的树苗恰好能够栽满面积为40平方米的空地,而要绿化的空地是一个长比宽多6
米的矩形,那么,矩形绿化带长为多少时,准备的树苗有剩余?
分析:设绿化带长为
x
米.
则依题意有
整理得
一元二次不等式
y
O
x
5
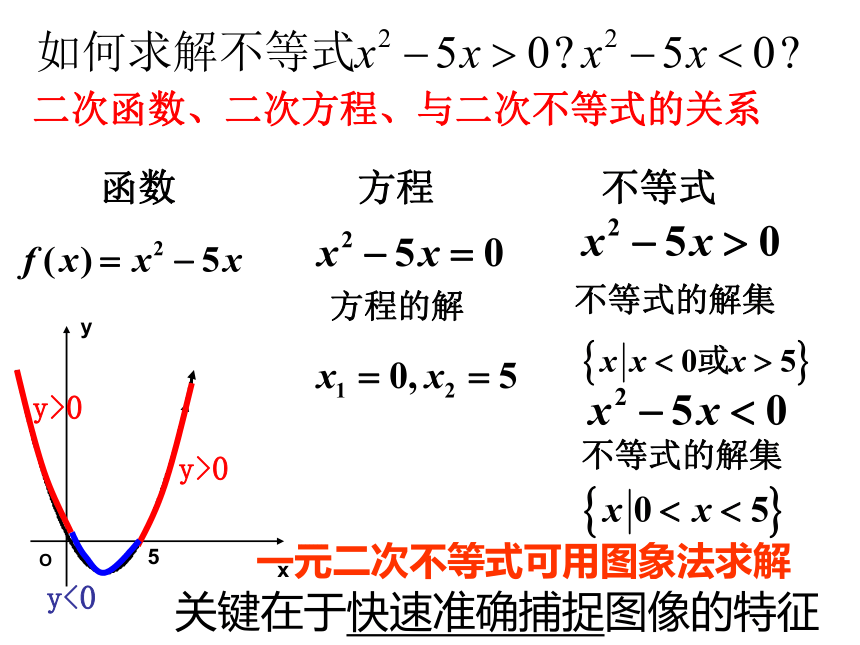
函数
方程
不等式
方程的解
不等式的解集
不等式的解集
二次函数、二次方程、与二次不等式的关系
关键在于快速准确捕捉图像的特征
一元二次不等式可用图象法求解
y>0
y>0
y<0
O
y
x
x1
x2
x1=x2
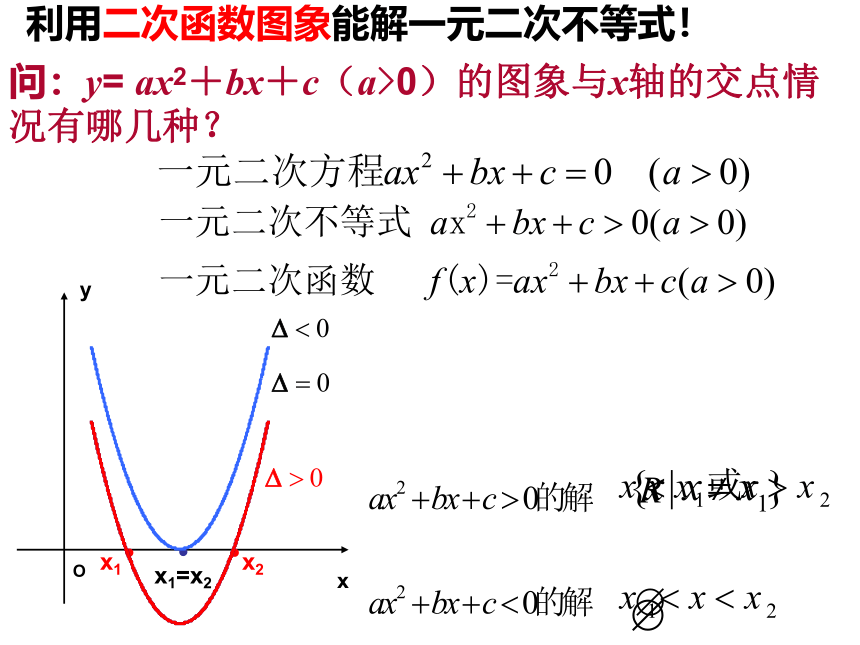
利用二次函数图象能解一元二次不等式!
问:y=
ax2+bx+c(a>0)的图象与x轴的交点情况有哪几种?
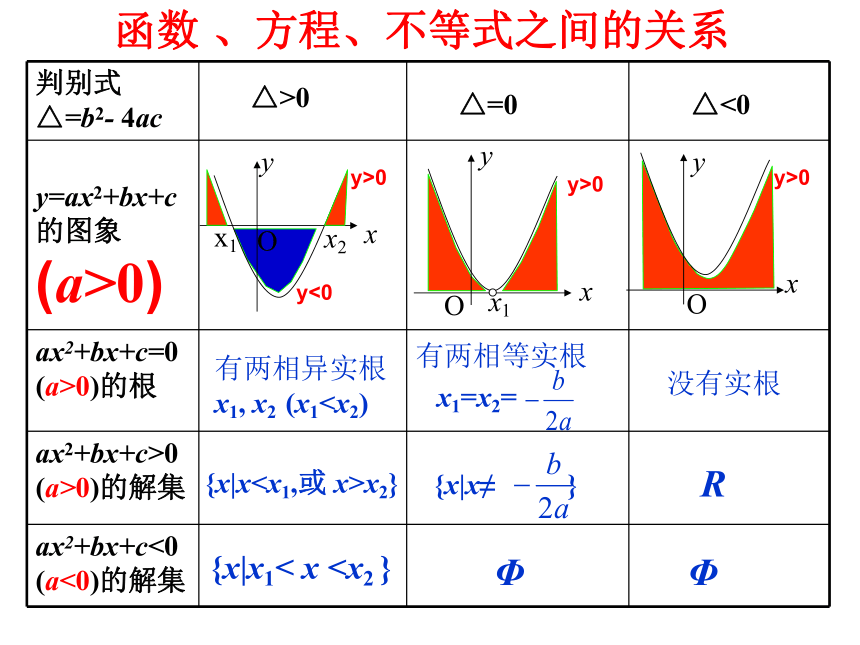
判别式
△=b2-
4ac
y=ax2+bx+c
的图象
(a>0)
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a<0)的解集
△>0
有两相异实根
x1,
x2
(x1{x|xx>x2}
{x|x1<
x
}
△=0
△<0
有两相等实根
x1=x2=
{x|x≠
}
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
函数
、方程、不等式之间的关系
y>0
y>0
y>0
y<0
例1.解不等式
2x2-3x-2
>
0
.
若改为:不等式
2x2-3x-2
<
0
.
注:开口向上,小于0
解集是大于小根且小于大根
图象为:
小结:利用一元二次函数图象解一元二次不等式的步骤
若a<0时,先变形!
一化:化二次项的系数为正数.
二判:判断对应方程的根.
三求:求对应方程的根.
四画:画出对应函数的图象.
五写:根据图象写出不等式的解集.
再看一例
练习1.解不等式
4x2-4x+1
>
0
解:因为△
=0,方程4x2-4x+1
=0的解是
所以,原不等式的解集是
注:4x2-4x+1
<0
无解
练习2.解不等式
解:
∵-x2+5x
+6>
0
x2
-
5x
-
6
<
0
∵方程的解
x2
-
5x
-
6
=0
的解是
所以,原不等式的解集是
练习3.
解不等式
-x2
+2x-3
>
0
略解:
-x2
+2x-3
>
0
x2
-2x+3
<
0
无
解
注:x2
-2x+3
>0
练习:求下列不等式的解集:
一化:化二次项的系数为正数.
二判:判断对应方程的根.
三求:求对应方程的根.
四画:画出对应函数的图象.
五写:根据图象写出不等式的解集.
(对应表)
小结:
2、利用一元二次函数图象解一元二次不等式的步骤
1、一元二次不等式的定义
作业
P80
习题3.2
A组
1
、2
练习:
函数
的定义域是
( )
A
例1.解不等式
2x2-3x-2
>
0
.
解:因为△
=(-3)2-4×2×(-2)>0,
方程的解2x2-3x-2
=0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
注:开口向上,大于0
解集是大于大根,小于小根
3.2
一元二次不等式及其解法
=
=
<
<
>
>
一元一次不等式可用图象法求解
练习1.求方程
的根?
复习:一元一次不等式的解法
今年的植树节我校高一年级的同学去植树时遇到一个这样的问题,我们准备的树苗恰好能够栽满面积为40平方米的空地,而要绿化的空地是一个长比宽多6
米的矩形,那么,矩形绿化带长为多少时,准备的树苗有剩余?
分析:设绿化带长为
x
米.
则依题意有
整理得
一元二次不等式
y
O
x
5
函数
方程
不等式
方程的解
不等式的解集
不等式的解集
二次函数、二次方程、与二次不等式的关系
关键在于快速准确捕捉图像的特征
一元二次不等式可用图象法求解
y>0
y>0
y<0
O
y
x
x1
x2
x1=x2
利用二次函数图象能解一元二次不等式!
问:y=
ax2+bx+c(a>0)的图象与x轴的交点情况有哪几种?
判别式
△=b2-
4ac
y=ax2+bx+c
的图象
(a>0)
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a<0)的解集
△>0
有两相异实根
x1,
x2
(x1
{x|x1<
x
△=0
△<0
有两相等实根
x1=x2=
{x|x≠
}
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
函数
、方程、不等式之间的关系
y>0
y>0
y>0
y<0
例1.解不等式
2x2-3x-2
>
0
.
若改为:不等式
2x2-3x-2
<
0
.
注:开口向上,小于0
解集是大于小根且小于大根
图象为:
小结:利用一元二次函数图象解一元二次不等式的步骤
若a<0时,先变形!
一化:化二次项的系数为正数.
二判:判断对应方程的根.
三求:求对应方程的根.
四画:画出对应函数的图象.
五写:根据图象写出不等式的解集.
再看一例
练习1.解不等式
4x2-4x+1
>
0
解:因为△
=0,方程4x2-4x+1
=0的解是
所以,原不等式的解集是
注:4x2-4x+1
<0
无解
练习2.解不等式
解:
∵-x2+5x
+6>
0
x2
-
5x
-
6
<
0
∵方程的解
x2
-
5x
-
6
=0
的解是
所以,原不等式的解集是
练习3.
解不等式
-x2
+2x-3
>
0
略解:
-x2
+2x-3
>
0
x2
-2x+3
<
0
无
解
注:x2
-2x+3
>0
练习:求下列不等式的解集:
一化:化二次项的系数为正数.
二判:判断对应方程的根.
三求:求对应方程的根.
四画:画出对应函数的图象.
五写:根据图象写出不等式的解集.
(对应表)
小结:
2、利用一元二次函数图象解一元二次不等式的步骤
1、一元二次不等式的定义
作业
P80
习题3.2
A组
1
、2
练习:
函数
的定义域是
( )
A
例1.解不等式
2x2-3x-2
>
0
.
解:因为△
=(-3)2-4×2×(-2)>0,
方程的解2x2-3x-2
=0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
注:开口向上,大于0
解集是大于大根,小于小根
