2021-2022学年人教版八年级上册12.3角的平分线的性质课件 (52张ppt共2课时)
文档属性
| 名称 | 2021-2022学年人教版八年级上册12.3角的平分线的性质课件 (52张ppt共2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 08:02:08 | ||
图片预览










文档简介
(共52张PPT)
第1课时
12.3
角的平分线的性质
九年级上册
RJ
初中数学
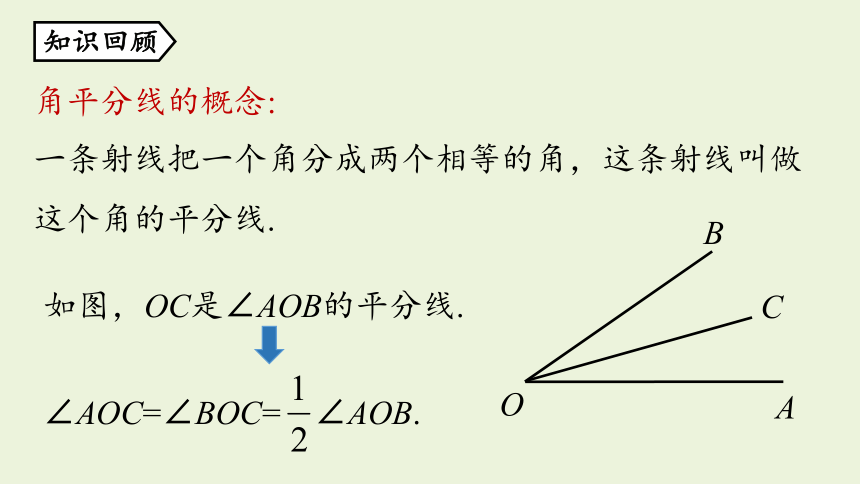
角平分线的概念:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,OC是∠AOB的平分线.
∠AOC=∠BOC=
∠AOB.
知识回顾
1.会用尺规作图法作一个角的平分线,知道作法的理论依据.
2.探究并证明角平分线的性质.
3.会用角平分线的性质解决实际问题.
学习目标
思考:如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个
角的平分线.
A
D
B
C
E
课堂导入
你能说明它的道理吗?
A
D
B
C
E
理由如下:如图构成了△ADC和△ABC,
∵在△ADC和△ABC中,
AD=AB,
AC=AC,
DC=BC,
∴△ADC≌△ABC(SSS),
∴
∠DAC=∠BAC.
∵点C在射线AE上,
∴AE是这个角的平分线.
课堂导入
如图,已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以M,N为圆心,大于
MN
的长为半径画弧,两弧在∠AOB的内部
相交于点C.
知识点1
作已知角的平分线
新知探究
C
B
N
O
M
A
(3)画射线OC,射线OC即为所求.
注意:(1)以“适当长为半径”是为了方便画图,不能太长,也不能太短.
(2)“以大于
MN的长为半径画弧”
是因为小于
MN的长为半径画弧时
两弧没有交点,等于
MN的长为半
径画弧时不容易操作.
C
B
N
O
M
A
(3)应该在角的内部找所作两弧的交点,因为所作的射线为角的平分线,而角的平分线应该在角的内部.
(4)“画射线OC
”不能说成“连接OC
”,
因为连接OC得到的是线段,而角
的平分线是一条射线.
C
B
N
O
M
A
如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
经过测量发现,PD=PE,在OC上再取几个点,都能得到同样的结论.
知识点2
角平分线的性质
新知探究
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
注意:(1)“点”是指角的平分线上任意位置的点;(2)“点到角的两边的距离”
是指点到角的两边的垂线段的长度.
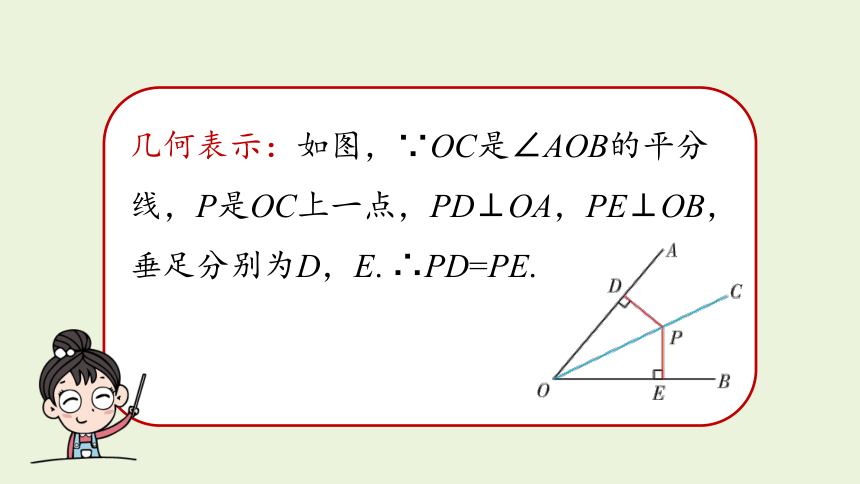
几何表示:如图,∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
例
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∠PDO=∠PEO,
∠AOC=∠BOC,
OP=OP,
∴△PDO≌△PEO(AAS),
∴PD=PE.
证明几何命题的一般步骤:
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证的结论
的途径,写出证明过程.
知识点3
证明几何命题的一般步骤
新知探究
注意:(1)所画图形应符合题意,并具有一般性和代表性.在画图的时候要考虑是否存在不同的情形,若存在,则要分别画出图形,再分别进行证明;
(2)证明过程中的每一步推理都要有依据,依据可以是已知条件、定义、定理等.
例1
求证:三角形的一边的两端点到这条边上的中线所在直线的距离相等.
解:已知:如图所示,AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.
求证:BE=CF.
跟踪训练
新知探究
可先将命题改写成“如果……那么……”的形式,然后确定已知和求证
证明:∵AD为△ABC的中线,∴BD=CD.
∵BE⊥AD交AD的延长线于点E,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED和△CFD中,∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BED≌△CFD(AAS),∴BE=CF.
例2
填空:下列结论一定成立的是(
)
①如图1,OC平分∠AOB,点P在OC上,D,E分别为OA,OB上的点,则PD=PE.
②如图2,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,则PD=PE.
O
B
A
C
P
D
图2
E
O
B
A
C
P
D
图1
E
┐
┐
(PD,PE不是角平分线上的点到角两边的距离)
(OC不一定是∠AOB的平分线)
③如图3,OC平分∠AOB,点P在OC上,PD⊥OA,垂足为D.若PD=3,则点P到OA的距离为3.
O
B
A
C
P
D
图3
(PD是∠AOB平分线OC上的点到OA的距离)
所以一定成立的是③.
1.如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,
F.求证:EB=FC.
证明:∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC,∴DE=DF.
∵在Rt△BDE和Rt△CDF中,BD=CD,
DE=DF,
∴Rt△BDE≌Rt△CDF(HL).
∴EB=FC.
C
A
B
D
F
E
┐
┐
随堂练习
2.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是(
)
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
B
解析:∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD.
在Rt△OCP和Rt△ODP中,
∵
OP=OP,
PC=PD,
∴Rt△OCP≌Rt△ODP(HL).
∴
∠CPO=∠DPO,OC=OD.
角的平分线的性质
会用尺规作图法画出一个已知角的平分线
性质
应用
角的平分线上的点到角的两边的距离相等
利用角的平分线的性质解决实际问题
课堂小结
1.如图,在△ABC中,∠C=90°,AC=BC,AD平分
∠CAB,交BC于点D,DE⊥AB,垂足为E,若AB=8cm,
则△DEB的周长为(
)
A.10cm
B.7cm
C.8cm
D.不能确定
拓展提升
解析:在△ABC中,∠C=90°,
∴DC⊥AC.
∵DE⊥AB,AD平分∠CAB,
∴DC=DE.
在Rt△ACD和Rt△AED中,
AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE.
∵AC=BC,∴AE=BC,∴△DEB的周长=DE+DB+
EB=DC+DB+EB=BC+EB=AE+EB=AB=8cm.
第2课时
12.3
角的平分线的性质
九年级上册
RJ
初中数学
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,点P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
O
A
B
C
P
D
E
┐
┐
知识回顾
1.探究并证明角的平分线的判定.
2.会用角的平分线的判定解决实际问题.
3.熟练掌握角的平分线的性质和角的平分线的判定的综合运用.
学习目标
思考:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处?
课堂导入
作出公路和铁路相交的角的平分线,按照比例尺的比例在该平分线上选取离交叉口处500m的位置即可建集贸市场.
到角的两边的距离相等的点是否在角的平分线上?
课堂导入
┐
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
注意:使用该判定定理的前提是这个点必须在角的内部.
O
A
B
C
P
D
E
┐
知识点1
角的平分线的判定
新知探究
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,∴点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO,∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC.
∴点P在∠AOB的平分线OC上.
例
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
角的平分线的性质定理与判定定理的关系.
点在角的平分线上
(角的内部)点到角的两边的距离相等
性质定理
判定定理
性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
知识点2
角的平分线的性质定理与判定定理的关系
新知探究
分别画出以下三角形的三个内角的角平分线,从位置的角度看你能得出什么结论?
三角形三个内角的角平分线的交点位于三角形的内部.
A
B
C
┐
A
B
C
A
B
C
知识点3
三角形三个内角平分线的性质
新知探究
过交点分别作三角形三边的垂线,测量一下每一组垂线段,从大小上你能观察出什么结论?
过交点作三角形三边的垂线段相等.
┐
┐
┐
┐
┐
┐
┐
┐
┐
A
B
C
A
B
B
C
A
C
例
如图,△ABC的角平分线AD,BE,CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,
垂足分别为点M,N,O.
┐
┐
┐
A
可多次利用角平分线的性质证得
∵AD为△ABC的角平分线,∴PN=PO.
∵BE为△ABC的角平分线,
∴PM=PO.
∵CF为△ABC的角平分线,
∴PM=PN.
∴PM=PN=PO,
即点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
┐
┐
┐
A
三角形三个内角的平分线的性质
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等.反之,三角形内部到三边距离相等的点是该
三角形三条角平分线的交点.
A
B
C
P
判断题:(1)如图1,若QM=QN,则OQ平分∠AOB.(
)
(2)如图2,若QM⊥OA于点M,QN⊥OB于点N,则OQ平分∠AOB.(
)
┐
┐
Q
O
B
A
M
图2
N
O
B
A
Q
M
图1
N
跟踪训练
新知探究
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
1.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确
的个数为(
)
A.0
B.1
C.2
D.3
D
C
A
E
B
D
F
P
┐
┐
随堂练习
2.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.
求证:AD是∠BAC的平分线.
┐
C
E
A
F
D
B
┐
BE=CF,DB=DC.
Rt△BDE≌Rt△CDF.
DE⊥AB,DF⊥AC
,DE=DF.
AD是∠BAC的平分线.
分析:
(直角三角形全等(HL))
(三角形全等的性质)
(角的平分线的判定)
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵在Rt△BDE和Rt△CDF中,
BE=CF,
DB=DC,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴点D在∠BAC的平分线上,
即AD是∠BAC的平分线.
┐
C
E
A
F
D
B
┐
3.如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
证明:由题意,得OD⊥BC,OE
⊥
AC,
OF
⊥
AB,
且OF=OD=OE,
∴OB,OC分别平分∠ABC和∠ACB.
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°.
4.如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
熟练掌握角的平分线的判定定理是解题的关键
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°,
∴∠ABC=∠EDC.
∵CE⊥AD,CF⊥AB,
∴∠CED=∠CFB=90°.
∵在△BCF和△DCE中,
∠CFB=∠CED,
∠FBC=∠EDC,
BC=DC,
∴△BCF≌△DCE(AAS).
∴CF=CE,即AC平分∠BAD.
E
A
B
C
D
F
┌
┐
角平分线的判定
学会用添加辅助线的方法解题
判定
定理
应用
角的内部到角的两边的距离相等的点在角的平分线上
综合利用角的平分线的性质和判定来解决实际问题
课堂小结
1.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE平分∠DAB.
A
B
C
E
D
┌
┌
拓展提升
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°,
∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC,
∴EC=EF.
证明角平分线的方法
只需从要证的线上的某一点向角的两边作(找)垂线段,再证明垂线段相等即可.
∵E是BC的中点,
∴EC=EB
=EF.
又∵EF⊥AD,EB⊥AB,
∴点E在∠DAB的平分线上,即AE平分∠DAB.
F
┌
A
B
C
E
D
┌
┌
2.如图,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°,
求证:点P在∠MON的平分线上.
C
D
A
B
P
O
M
N
┌
┌
证明:①若∠PAO≠90°,如图,过点P分别作PC⊥OM,PD⊥ON,垂足分别为C,D,则∠ACP=∠BDP=90°.
在四边形OCPD中,
∠CPD=360°-∠OCP-∠COD-∠ODP=120°,
∴∠APB=∠CPD.
∴∠APB-∠APD
=∠CPD-∠APD,即∠APC=∠BPD.
在△APC和△BPD中,
∠APC=∠BPD,
∠ACP=∠BDP,
AP=BP,
∴△APC≌△BPD(AAS).
∴PC=PD,
∴点P在∠MON的平分线上.
C
D
A
B
P
O
M
N
┌
┌
A
B
P
O
M
N
②若∠PAO=90°,则∠PBO=360°-∠APB-
∠PAO
-∠AOB
=
90°
,
∴PA=PB,
∴点P在∠MON的平分线上.
综上,点P在∠MON的平分线上.
∠PAO的度数未知,因分情况讨论,确保结果的完整性.
第1课时
12.3
角的平分线的性质
九年级上册
RJ
初中数学
角平分线的概念:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,OC是∠AOB的平分线.
∠AOC=∠BOC=
∠AOB.
知识回顾
1.会用尺规作图法作一个角的平分线,知道作法的理论依据.
2.探究并证明角平分线的性质.
3.会用角平分线的性质解决实际问题.
学习目标
思考:如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个
角的平分线.
A
D
B
C
E
课堂导入
你能说明它的道理吗?
A
D
B
C
E
理由如下:如图构成了△ADC和△ABC,
∵在△ADC和△ABC中,
AD=AB,
AC=AC,
DC=BC,
∴△ADC≌△ABC(SSS),
∴
∠DAC=∠BAC.
∵点C在射线AE上,
∴AE是这个角的平分线.
课堂导入
如图,已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以M,N为圆心,大于
MN
的长为半径画弧,两弧在∠AOB的内部
相交于点C.
知识点1
作已知角的平分线
新知探究
C
B
N
O
M
A
(3)画射线OC,射线OC即为所求.
注意:(1)以“适当长为半径”是为了方便画图,不能太长,也不能太短.
(2)“以大于
MN的长为半径画弧”
是因为小于
MN的长为半径画弧时
两弧没有交点,等于
MN的长为半
径画弧时不容易操作.
C
B
N
O
M
A
(3)应该在角的内部找所作两弧的交点,因为所作的射线为角的平分线,而角的平分线应该在角的内部.
(4)“画射线OC
”不能说成“连接OC
”,
因为连接OC得到的是线段,而角
的平分线是一条射线.
C
B
N
O
M
A
如图,任意作一个角∠AOB,作出∠AOB的平分线OC.在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
经过测量发现,PD=PE,在OC上再取几个点,都能得到同样的结论.
知识点2
角平分线的性质
新知探究
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
注意:(1)“点”是指角的平分线上任意位置的点;(2)“点到角的两边的距离”
是指点到角的两边的垂线段的长度.
几何表示:如图,∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
例
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∠PDO=∠PEO,
∠AOC=∠BOC,
OP=OP,
∴△PDO≌△PEO(AAS),
∴PD=PE.
证明几何命题的一般步骤:
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证的结论
的途径,写出证明过程.
知识点3
证明几何命题的一般步骤
新知探究
注意:(1)所画图形应符合题意,并具有一般性和代表性.在画图的时候要考虑是否存在不同的情形,若存在,则要分别画出图形,再分别进行证明;
(2)证明过程中的每一步推理都要有依据,依据可以是已知条件、定义、定理等.
例1
求证:三角形的一边的两端点到这条边上的中线所在直线的距离相等.
解:已知:如图所示,AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.
求证:BE=CF.
跟踪训练
新知探究
可先将命题改写成“如果……那么……”的形式,然后确定已知和求证
证明:∵AD为△ABC的中线,∴BD=CD.
∵BE⊥AD交AD的延长线于点E,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED和△CFD中,∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BED≌△CFD(AAS),∴BE=CF.
例2
填空:下列结论一定成立的是(
)
①如图1,OC平分∠AOB,点P在OC上,D,E分别为OA,OB上的点,则PD=PE.
②如图2,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,则PD=PE.
O
B
A
C
P
D
图2
E
O
B
A
C
P
D
图1
E
┐
┐
(PD,PE不是角平分线上的点到角两边的距离)
(OC不一定是∠AOB的平分线)
③如图3,OC平分∠AOB,点P在OC上,PD⊥OA,垂足为D.若PD=3,则点P到OA的距离为3.
O
B
A
C
P
D
图3
(PD是∠AOB平分线OC上的点到OA的距离)
所以一定成立的是③.
1.如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,
F.求证:EB=FC.
证明:∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC,∴DE=DF.
∵在Rt△BDE和Rt△CDF中,BD=CD,
DE=DF,
∴Rt△BDE≌Rt△CDF(HL).
∴EB=FC.
C
A
B
D
F
E
┐
┐
随堂练习
2.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是(
)
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
B
解析:∵OP为∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD.
在Rt△OCP和Rt△ODP中,
∵
OP=OP,
PC=PD,
∴Rt△OCP≌Rt△ODP(HL).
∴
∠CPO=∠DPO,OC=OD.
角的平分线的性质
会用尺规作图法画出一个已知角的平分线
性质
应用
角的平分线上的点到角的两边的距离相等
利用角的平分线的性质解决实际问题
课堂小结
1.如图,在△ABC中,∠C=90°,AC=BC,AD平分
∠CAB,交BC于点D,DE⊥AB,垂足为E,若AB=8cm,
则△DEB的周长为(
)
A.10cm
B.7cm
C.8cm
D.不能确定
拓展提升
解析:在△ABC中,∠C=90°,
∴DC⊥AC.
∵DE⊥AB,AD平分∠CAB,
∴DC=DE.
在Rt△ACD和Rt△AED中,
AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE.
∵AC=BC,∴AE=BC,∴△DEB的周长=DE+DB+
EB=DC+DB+EB=BC+EB=AE+EB=AB=8cm.
第2课时
12.3
角的平分线的性质
九年级上册
RJ
初中数学
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,点P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
O
A
B
C
P
D
E
┐
┐
知识回顾
1.探究并证明角的平分线的判定.
2.会用角的平分线的判定解决实际问题.
3.熟练掌握角的平分线的性质和角的平分线的判定的综合运用.
学习目标
思考:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处?
课堂导入
作出公路和铁路相交的角的平分线,按照比例尺的比例在该平分线上选取离交叉口处500m的位置即可建集贸市场.
到角的两边的距离相等的点是否在角的平分线上?
课堂导入
┐
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
注意:使用该判定定理的前提是这个点必须在角的内部.
O
A
B
C
P
D
E
┐
知识点1
角的平分线的判定
新知探究
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,∴点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO,∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC.
∴点P在∠AOB的平分线OC上.
例
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
角的平分线的性质定理与判定定理的关系.
点在角的平分线上
(角的内部)点到角的两边的距离相等
性质定理
判定定理
性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
知识点2
角的平分线的性质定理与判定定理的关系
新知探究
分别画出以下三角形的三个内角的角平分线,从位置的角度看你能得出什么结论?
三角形三个内角的角平分线的交点位于三角形的内部.
A
B
C
┐
A
B
C
A
B
C
知识点3
三角形三个内角平分线的性质
新知探究
过交点分别作三角形三边的垂线,测量一下每一组垂线段,从大小上你能观察出什么结论?
过交点作三角形三边的垂线段相等.
┐
┐
┐
┐
┐
┐
┐
┐
┐
A
B
C
A
B
B
C
A
C
例
如图,△ABC的角平分线AD,BE,CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,
垂足分别为点M,N,O.
┐
┐
┐
A
可多次利用角平分线的性质证得
∵AD为△ABC的角平分线,∴PN=PO.
∵BE为△ABC的角平分线,
∴PM=PO.
∵CF为△ABC的角平分线,
∴PM=PN.
∴PM=PN=PO,
即点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
┐
┐
┐
A
三角形三个内角的平分线的性质
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等.反之,三角形内部到三边距离相等的点是该
三角形三条角平分线的交点.
A
B
C
P
判断题:(1)如图1,若QM=QN,则OQ平分∠AOB.(
)
(2)如图2,若QM⊥OA于点M,QN⊥OB于点N,则OQ平分∠AOB.(
)
┐
┐
Q
O
B
A
M
图2
N
O
B
A
Q
M
图1
N
跟踪训练
新知探究
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
1.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确
的个数为(
)
A.0
B.1
C.2
D.3
D
C
A
E
B
D
F
P
┐
┐
随堂练习
2.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.
求证:AD是∠BAC的平分线.
┐
C
E
A
F
D
B
┐
BE=CF,DB=DC.
Rt△BDE≌Rt△CDF.
DE⊥AB,DF⊥AC
,DE=DF.
AD是∠BAC的平分线.
分析:
(直角三角形全等(HL))
(三角形全等的性质)
(角的平分线的判定)
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵在Rt△BDE和Rt△CDF中,
BE=CF,
DB=DC,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴点D在∠BAC的平分线上,
即AD是∠BAC的平分线.
┐
C
E
A
F
D
B
┐
3.如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
证明:由题意,得OD⊥BC,OE
⊥
AC,
OF
⊥
AB,
且OF=OD=OE,
∴OB,OC分别平分∠ABC和∠ACB.
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°.
4.如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
熟练掌握角的平分线的判定定理是解题的关键
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°,
∴∠ABC=∠EDC.
∵CE⊥AD,CF⊥AB,
∴∠CED=∠CFB=90°.
∵在△BCF和△DCE中,
∠CFB=∠CED,
∠FBC=∠EDC,
BC=DC,
∴△BCF≌△DCE(AAS).
∴CF=CE,即AC平分∠BAD.
E
A
B
C
D
F
┌
┐
角平分线的判定
学会用添加辅助线的方法解题
判定
定理
应用
角的内部到角的两边的距离相等的点在角的平分线上
综合利用角的平分线的性质和判定来解决实际问题
课堂小结
1.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE平分∠DAB.
A
B
C
E
D
┌
┌
拓展提升
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°,
∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC,
∴EC=EF.
证明角平分线的方法
只需从要证的线上的某一点向角的两边作(找)垂线段,再证明垂线段相等即可.
∵E是BC的中点,
∴EC=EB
=EF.
又∵EF⊥AD,EB⊥AB,
∴点E在∠DAB的平分线上,即AE平分∠DAB.
F
┌
A
B
C
E
D
┌
┌
2.如图,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°,
求证:点P在∠MON的平分线上.
C
D
A
B
P
O
M
N
┌
┌
证明:①若∠PAO≠90°,如图,过点P分别作PC⊥OM,PD⊥ON,垂足分别为C,D,则∠ACP=∠BDP=90°.
在四边形OCPD中,
∠CPD=360°-∠OCP-∠COD-∠ODP=120°,
∴∠APB=∠CPD.
∴∠APB-∠APD
=∠CPD-∠APD,即∠APC=∠BPD.
在△APC和△BPD中,
∠APC=∠BPD,
∠ACP=∠BDP,
AP=BP,
∴△APC≌△BPD(AAS).
∴PC=PD,
∴点P在∠MON的平分线上.
C
D
A
B
P
O
M
N
┌
┌
A
B
P
O
M
N
②若∠PAO=90°,则∠PBO=360°-∠APB-
∠PAO
-∠AOB
=
90°
,
∴PA=PB,
∴点P在∠MON的平分线上.
综上,点P在∠MON的平分线上.
∠PAO的度数未知,因分情况讨论,确保结果的完整性.
