专题5 直线的方程 专题集训 -2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案解析)
文档属性
| 名称 | 专题5 直线的方程 专题集训 -2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 370.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 14:24:18 | ||
图片预览




文档简介
2021-2022学年高二数学(人教A版2019选择性必修一)
专题5
直线的方程
一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.直线l过点(-1,-1)和(2,5),点(1
010,b)在直线l上,则b的值为(
)
A.2
019
B.2
020
C.2
021
D.2
022
2.在等腰三角形AOB中,AO=AB,点O(0,0),A(1,3),点B在x轴的正半轴上,则直线AB的方程为( )
A.y-1=3(x-3)
B.y-1=-3(x-3)
C.y-3=3(x-1)
D.y-3=-3(x-1)
3.直线的倾斜角和所经过的定点分别是(
)
A.30°,(-3,4)
B.120°,(-3,4)
C.150°,(3,-4)
D.120°,(3,-4)
4.已知直线的方程是,则
A.直线经过点),斜率为
B.直线经过点,斜率为
C.直线经过点,斜率为
D.直线经过点,斜率为
5.“”是“直线和直线平行且不重合”的(
).
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
6.已知,则直线通过( )
象限
A.第一、二、三
B.第一、二、四
C.第一、三、四
D.第二、三、四
7.两条直线=1与=1在同一平面直角坐标系中的图象是下图中的(
)
A.
B.
C.
D.
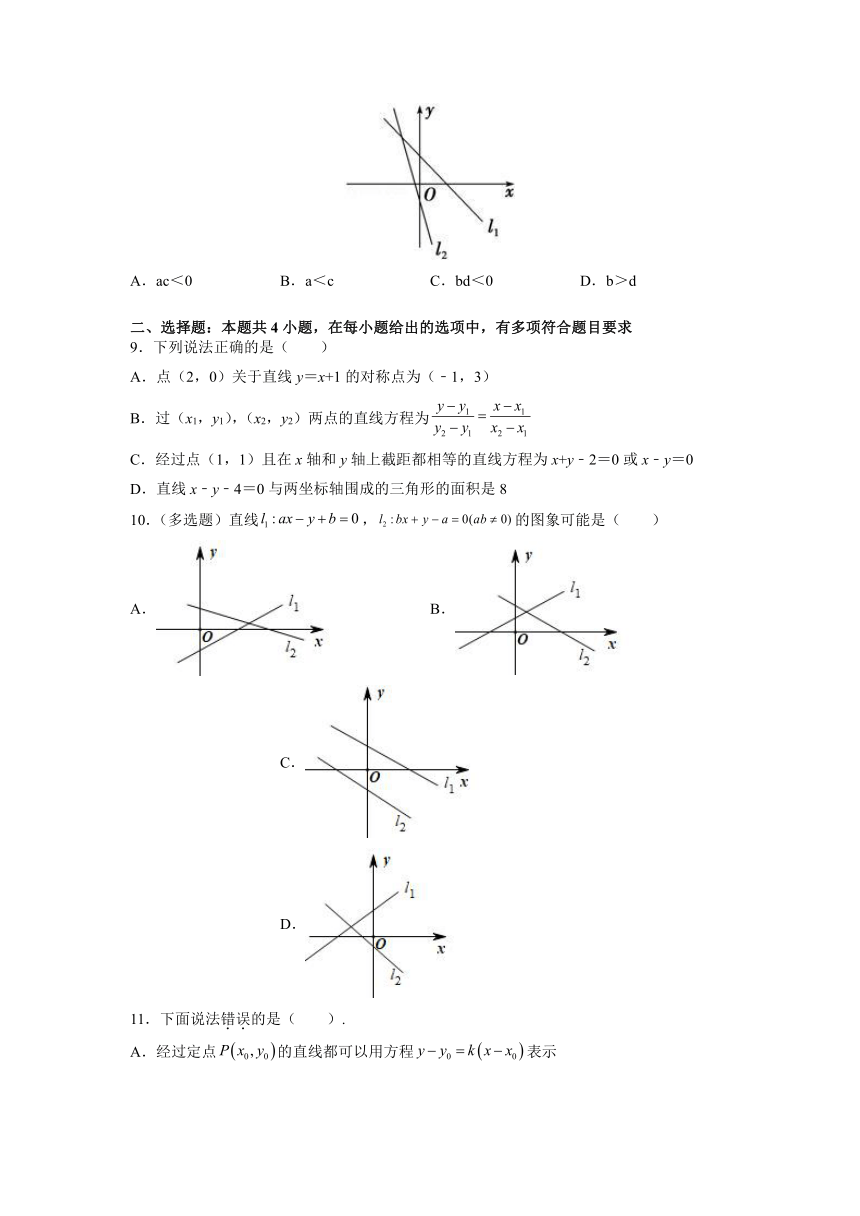
8.已知直线l1,l2的方程分别为x+ay+b=0,x+cy+d=0,其图象如图所示,则有
A.ac<0
B.a<c
C.bd<0
D.b>d
二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求
9.下列说法正确的是(
)
A.点(2,0)关于直线y=x+1的对称点为(﹣1,3)
B.过(x1,y1),(x2,y2)两点的直线方程为
C.经过点(1,1)且在x轴和y轴上截距都相等的直线方程为x+y﹣2=0或x﹣y=0
D.直线x﹣y﹣4=0与两坐标轴围成的三角形的面积是8
10.(多选题)直线,的图象可能是(
)
A.
B.
C.
D.
11.下面说法错误的是(
).
A.经过定点的直线都可以用方程表示
B.不经过原点的直线都可以用方程表示
C.经过定点的直线都可以用方程表示
D.经过任意两个不同的点的直线都可以用方程表示
12.下列说法正确的是(
)
A.直线必过定点
B.直线在轴上的截距为
C.直线的倾斜角为60°
D.过点且垂直于直线的直线方程为
三、填空题:本题共4小题
13.若直线的倾斜角是,则实数是_______________.
14.求经过两点的直线方程___________.
15.无论k取何值,直线y-2=k(x+1)所过的定点是____.
16.如图直线y=kx+b通过第一、三、四象限,则k__,b__.
四、解答题:本题共6小题.解答应写出文字说明、证明过程或演算步骤
17.直线l经过点P(3,4),它的倾斜角是直线y=x+的倾斜角的2倍,求直线l的点斜式方程.
18.已知直线的倾斜角是直线l的倾斜角的5倍,分别求满足下列条件的直线l的方程.
(1)过点,
(2)在x轴上截距为;
(3)在y轴上截距为3.
19.在中,已知,,且AC边的中点M在y轴上,BC边的中点N在x轴上,求:
顶点C的坐标;?
直线MN的方程.
20.如图所示,在平面直角坐标系中,已知矩形的长为2,宽为1,边分别在轴、轴的正半轴上,点与坐标原点重合.将矩形折叠,使点落在线段上.若折痕所在直线的斜率为,试写出折痕所在的直线方程.
21.求满足下列条件的直线方程:
(1)经过点,且与直线垂直;
(2)与直线平行,与直线在y轴上的截距相同.
22.直线过点P且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
参考答案
1.C
【解析】因为直线l过点(-1,-1)和(2,5),
所以直线l的两点式方程为,
化简得y=2x+1,
将x=1
010代入,得b=2
021.
故选:C
2.D
【解析】在等腰三角形AOB中,AO=AB,点O(0,0),A(1,3),
点B在x轴的正半轴上,由等腰三角形的对称性可知点B(2,0),直线AB斜率k=-3
则直线AB方程为:y-3=-3(x-1)
故选D
3.B
【解析】根据直线可以得到斜率,过定点(-3,4).
所以倾斜角120°.
故选:B.
4.C
【解析】直线的方程可化为,故直线经过点,斜率为.
故选C.
5.C
【解析】当时,两直线分别为:,,
∴两直线斜率相等且,
∴两条直线平行且不重合;
若两直线平行且不重合,则,∴,综上所述,是两直线平行且不重合的充要条件,
故选:C.
6.A
【解析】因为,所以,
①若则,,直线通过第一、二、三象限.
②若则,,直线通过第一、二、三象限.
7.B
【解析】两直线的方程分别化为y=x-n,y=x-m,易知两直线的斜率符号相同,结合选项可知,B符合,
故选:B
8.C
【解析】直线方程化为l1:y=﹣x﹣,l2:y=﹣x﹣.
由图象知,﹣<﹣<0,﹣>0>﹣,
∴a>c>0,b<0,d>0.
故选C
9.ACD
【解析】点(2,0)与(﹣1,3)的中点(,)
满足直线y=x+1,并且两点的斜率为﹣1,
所以点(2,0)关于直线y=x+1的对称点为(﹣1,3),
所以A正确;
当x1≠x2,y1≠y2时,过(x1,y1),(x2,y2),
两点的直线方程为,所以B不正确;
经过点(1,1)且在x轴和y轴上截距都相等的直线方程
为x+y﹣2=0或x﹣y=0,所以正确;
直线x﹣y﹣4=0,当x=0时,y=﹣4,当y=0时,x=4,
所以直线与两坐标轴围成的三角形的面积是:8,所以D正确;
故选:ACD.
10.BC
【解析】解:直线的方程是,可化为,
的方程是,可化为,
在A中,假设直线正确:由知,则,与的图象不符;
在B中,假设直线正确:由知,则,与的图象相符;
在C中,假设直线正确:由知,则,与的图象相符;
在D中,假设直线正确:由知,则,与的图象不符.
故选:BC.
11.ABC
【解析】经过定点且斜率存在的直线才可用方程表示,所以A错;
不经过原点且与两坐标轴都不垂直的直线才可以用方程表示,所以B错;
经过定点且斜率存在的直线才可用方程表示,所以C错;
当时,经过点的直线可以用方程即表示,当时,经过点的直线可以用方程,即表示,因此经过任意两个不同的点的直线都可以用方程表示,所以D对;
故选:ABC
12.ABD
【解析】可化为,则直线必过定点,故A正确;
令,则,即直线在轴上的截距为,故B正确;
可化为,则该直线的斜率为,即倾斜角为,故C错误;
设过点且垂直于直线的直线的斜率为
因为直线的斜率为,所以,解得
则过点且垂直于直线的直线的方程为,即,故D正确;
故选:ABD
13.
【解析】因为直线的倾斜角是,
所以直线的斜率为
因此
或(舍)
故答案为:
14.
【解析】直线方程为,即.
15.
【解析】联立方程组得,所以直线恒过定点,
故答案为:.
16.k>0
b<0
【解析】由图可知,直线的倾斜角为锐角,在纵轴上的截距为负,
所以k>0,b<0.
故答案为:k>0;b<0.
17.y-4=(x-3).
【解析】直线的斜率k=,
则其倾斜角α=60°,所以直线l的倾斜角为120°.
以直线l的斜率为k′=tan
120°=-.
所以直线l的点斜式方程为y-4=-(x-3).
18.(1)y=x--4.(2)
y=x+
(3)
y=x+3.
【解析】直线y=-x+5的斜率k=tanα=-,∴α=150°.(1)代入已知点得到直线方程.(2)在x轴上截距为-2,故过点(-2,0),代入方成即可.(3)在y轴上截距为3,故过点(0,3)点斜式写出直线方程即可.
直线y=-x+5的斜率k=tanα=-,
∴α=150°,
故所求直线l的倾斜角为30°,斜率k′=.
(1)过点P(3,-4),由点斜式方程得:
y+4=
(x-3),
∴y=x--4.
(2)在x轴截距为-2,即直线l过点(-2,0),
由点斜式方程得:y-0=
(x+2),∴y=x+.
(3)在y轴上截距为3,由斜截式方程得y=x+3.
19.(1);(2).
【解析】(1)边AC的中点M在y轴上,由中点公式得,A,C两点的横坐标和的平均数为0,同理,B,C两点的纵坐标和的平均数为0.构造方程易得C点的坐标.
(2)根据C点的坐标,结合中点公式,我们可求出M,N两点的坐标,代入两点式即可求出直线MN的方程.
解:(1)设点C(x,y),
∵边AC的中点M在y轴上得=0,
∵边BC的中点N在x轴上得=0,
解得x=﹣5,y=﹣3.
故所求点C的坐标是(﹣5,﹣3).
(2)点M的坐标是(0,﹣),
点N的坐标是(1,0),
直线MN的方程是=,
即5x﹣2y﹣5=0.
20.
【解析】当时,与重合,折痕所在直线方程为;
当时,点关于折痕对称点在上.
设点的坐标为,则,
直线的方程为,时满足,
综上所述:直线的方程为.
21.(1);(2).
【解析】(1)由题意,直线的斜率为3,
因为所求直线与该直线垂直,所以所求直线斜率为,
又直线过点,
由直线方程的点斜式方程可得,即.
(2)直线的斜率为,直线在y轴上的截距为,
由题意知,所求直线的斜率为,在轴上的截距为,
由直线方程的斜截式得,即.
22.+=1.
【解析】
设直线方程为+=1(a>0,b>0),
若满足条件(1),则a+b+=12,①
又∵直线过点P(,2),∵+=1.②
由①②可得5a2-32a+48=0,
解得,或.
∴所求直线的方程为+=1或+=1,
即3x+4y-12=0或15x+8y-36=0.
若满足条件(2),则ab=12,③
由题意得,+=1,④
由③④整理得a2-6a+8=0,
解得,或.
∴所求直线的方程为+=1或+=1,
即3x+4y-12=0或3x+y-6=0.
综上所述:存在同时满足(1)(2)两个条件的直线方程,为3x+4y-12=0.
专题5
直线的方程
一、选择题:本题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的
1.直线l过点(-1,-1)和(2,5),点(1
010,b)在直线l上,则b的值为(
)
A.2
019
B.2
020
C.2
021
D.2
022
2.在等腰三角形AOB中,AO=AB,点O(0,0),A(1,3),点B在x轴的正半轴上,则直线AB的方程为( )
A.y-1=3(x-3)
B.y-1=-3(x-3)
C.y-3=3(x-1)
D.y-3=-3(x-1)
3.直线的倾斜角和所经过的定点分别是(
)
A.30°,(-3,4)
B.120°,(-3,4)
C.150°,(3,-4)
D.120°,(3,-4)
4.已知直线的方程是,则
A.直线经过点),斜率为
B.直线经过点,斜率为
C.直线经过点,斜率为
D.直线经过点,斜率为
5.“”是“直线和直线平行且不重合”的(
).
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
6.已知,则直线通过( )
象限
A.第一、二、三
B.第一、二、四
C.第一、三、四
D.第二、三、四
7.两条直线=1与=1在同一平面直角坐标系中的图象是下图中的(
)
A.
B.
C.
D.
8.已知直线l1,l2的方程分别为x+ay+b=0,x+cy+d=0,其图象如图所示,则有
A.ac<0
B.a<c
C.bd<0
D.b>d
二、选择题:本题共4小题,在每小题给出的选项中,有多项符合题目要求
9.下列说法正确的是(
)
A.点(2,0)关于直线y=x+1的对称点为(﹣1,3)
B.过(x1,y1),(x2,y2)两点的直线方程为
C.经过点(1,1)且在x轴和y轴上截距都相等的直线方程为x+y﹣2=0或x﹣y=0
D.直线x﹣y﹣4=0与两坐标轴围成的三角形的面积是8
10.(多选题)直线,的图象可能是(
)
A.
B.
C.
D.
11.下面说法错误的是(
).
A.经过定点的直线都可以用方程表示
B.不经过原点的直线都可以用方程表示
C.经过定点的直线都可以用方程表示
D.经过任意两个不同的点的直线都可以用方程表示
12.下列说法正确的是(
)
A.直线必过定点
B.直线在轴上的截距为
C.直线的倾斜角为60°
D.过点且垂直于直线的直线方程为
三、填空题:本题共4小题
13.若直线的倾斜角是,则实数是_______________.
14.求经过两点的直线方程___________.
15.无论k取何值,直线y-2=k(x+1)所过的定点是____.
16.如图直线y=kx+b通过第一、三、四象限,则k__,b__.
四、解答题:本题共6小题.解答应写出文字说明、证明过程或演算步骤
17.直线l经过点P(3,4),它的倾斜角是直线y=x+的倾斜角的2倍,求直线l的点斜式方程.
18.已知直线的倾斜角是直线l的倾斜角的5倍,分别求满足下列条件的直线l的方程.
(1)过点,
(2)在x轴上截距为;
(3)在y轴上截距为3.
19.在中,已知,,且AC边的中点M在y轴上,BC边的中点N在x轴上,求:
顶点C的坐标;?
直线MN的方程.
20.如图所示,在平面直角坐标系中,已知矩形的长为2,宽为1,边分别在轴、轴的正半轴上,点与坐标原点重合.将矩形折叠,使点落在线段上.若折痕所在直线的斜率为,试写出折痕所在的直线方程.
21.求满足下列条件的直线方程:
(1)经过点,且与直线垂直;
(2)与直线平行,与直线在y轴上的截距相同.
22.直线过点P且与x轴、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.
参考答案
1.C
【解析】因为直线l过点(-1,-1)和(2,5),
所以直线l的两点式方程为,
化简得y=2x+1,
将x=1
010代入,得b=2
021.
故选:C
2.D
【解析】在等腰三角形AOB中,AO=AB,点O(0,0),A(1,3),
点B在x轴的正半轴上,由等腰三角形的对称性可知点B(2,0),直线AB斜率k=-3
则直线AB方程为:y-3=-3(x-1)
故选D
3.B
【解析】根据直线可以得到斜率,过定点(-3,4).
所以倾斜角120°.
故选:B.
4.C
【解析】直线的方程可化为,故直线经过点,斜率为.
故选C.
5.C
【解析】当时,两直线分别为:,,
∴两直线斜率相等且,
∴两条直线平行且不重合;
若两直线平行且不重合,则,∴,综上所述,是两直线平行且不重合的充要条件,
故选:C.
6.A
【解析】因为,所以,
①若则,,直线通过第一、二、三象限.
②若则,,直线通过第一、二、三象限.
7.B
【解析】两直线的方程分别化为y=x-n,y=x-m,易知两直线的斜率符号相同,结合选项可知,B符合,
故选:B
8.C
【解析】直线方程化为l1:y=﹣x﹣,l2:y=﹣x﹣.
由图象知,﹣<﹣<0,﹣>0>﹣,
∴a>c>0,b<0,d>0.
故选C
9.ACD
【解析】点(2,0)与(﹣1,3)的中点(,)
满足直线y=x+1,并且两点的斜率为﹣1,
所以点(2,0)关于直线y=x+1的对称点为(﹣1,3),
所以A正确;
当x1≠x2,y1≠y2时,过(x1,y1),(x2,y2),
两点的直线方程为,所以B不正确;
经过点(1,1)且在x轴和y轴上截距都相等的直线方程
为x+y﹣2=0或x﹣y=0,所以正确;
直线x﹣y﹣4=0,当x=0时,y=﹣4,当y=0时,x=4,
所以直线与两坐标轴围成的三角形的面积是:8,所以D正确;
故选:ACD.
10.BC
【解析】解:直线的方程是,可化为,
的方程是,可化为,
在A中,假设直线正确:由知,则,与的图象不符;
在B中,假设直线正确:由知,则,与的图象相符;
在C中,假设直线正确:由知,则,与的图象相符;
在D中,假设直线正确:由知,则,与的图象不符.
故选:BC.
11.ABC
【解析】经过定点且斜率存在的直线才可用方程表示,所以A错;
不经过原点且与两坐标轴都不垂直的直线才可以用方程表示,所以B错;
经过定点且斜率存在的直线才可用方程表示,所以C错;
当时,经过点的直线可以用方程即表示,当时,经过点的直线可以用方程,即表示,因此经过任意两个不同的点的直线都可以用方程表示,所以D对;
故选:ABC
12.ABD
【解析】可化为,则直线必过定点,故A正确;
令,则,即直线在轴上的截距为,故B正确;
可化为,则该直线的斜率为,即倾斜角为,故C错误;
设过点且垂直于直线的直线的斜率为
因为直线的斜率为,所以,解得
则过点且垂直于直线的直线的方程为,即,故D正确;
故选:ABD
13.
【解析】因为直线的倾斜角是,
所以直线的斜率为
因此
或(舍)
故答案为:
14.
【解析】直线方程为,即.
15.
【解析】联立方程组得,所以直线恒过定点,
故答案为:.
16.k>0
b<0
【解析】由图可知,直线的倾斜角为锐角,在纵轴上的截距为负,
所以k>0,b<0.
故答案为:k>0;b<0.
17.y-4=(x-3).
【解析】直线的斜率k=,
则其倾斜角α=60°,所以直线l的倾斜角为120°.
以直线l的斜率为k′=tan
120°=-.
所以直线l的点斜式方程为y-4=-(x-3).
18.(1)y=x--4.(2)
y=x+
(3)
y=x+3.
【解析】直线y=-x+5的斜率k=tanα=-,∴α=150°.(1)代入已知点得到直线方程.(2)在x轴上截距为-2,故过点(-2,0),代入方成即可.(3)在y轴上截距为3,故过点(0,3)点斜式写出直线方程即可.
直线y=-x+5的斜率k=tanα=-,
∴α=150°,
故所求直线l的倾斜角为30°,斜率k′=.
(1)过点P(3,-4),由点斜式方程得:
y+4=
(x-3),
∴y=x--4.
(2)在x轴截距为-2,即直线l过点(-2,0),
由点斜式方程得:y-0=
(x+2),∴y=x+.
(3)在y轴上截距为3,由斜截式方程得y=x+3.
19.(1);(2).
【解析】(1)边AC的中点M在y轴上,由中点公式得,A,C两点的横坐标和的平均数为0,同理,B,C两点的纵坐标和的平均数为0.构造方程易得C点的坐标.
(2)根据C点的坐标,结合中点公式,我们可求出M,N两点的坐标,代入两点式即可求出直线MN的方程.
解:(1)设点C(x,y),
∵边AC的中点M在y轴上得=0,
∵边BC的中点N在x轴上得=0,
解得x=﹣5,y=﹣3.
故所求点C的坐标是(﹣5,﹣3).
(2)点M的坐标是(0,﹣),
点N的坐标是(1,0),
直线MN的方程是=,
即5x﹣2y﹣5=0.
20.
【解析】当时,与重合,折痕所在直线方程为;
当时,点关于折痕对称点在上.
设点的坐标为,则,
直线的方程为,时满足,
综上所述:直线的方程为.
21.(1);(2).
【解析】(1)由题意,直线的斜率为3,
因为所求直线与该直线垂直,所以所求直线斜率为,
又直线过点,
由直线方程的点斜式方程可得,即.
(2)直线的斜率为,直线在y轴上的截距为,
由题意知,所求直线的斜率为,在轴上的截距为,
由直线方程的斜截式得,即.
22.+=1.
【解析】
设直线方程为+=1(a>0,b>0),
若满足条件(1),则a+b+=12,①
又∵直线过点P(,2),∵+=1.②
由①②可得5a2-32a+48=0,
解得,或.
∴所求直线的方程为+=1或+=1,
即3x+4y-12=0或15x+8y-36=0.
若满足条件(2),则ab=12,③
由题意得,+=1,④
由③④整理得a2-6a+8=0,
解得,或.
∴所求直线的方程为+=1或+=1,
即3x+4y-12=0或3x+y-6=0.
综上所述:存在同时满足(1)(2)两个条件的直线方程,为3x+4y-12=0.
