2020-2021学年安徽省淮北市七年级(下)期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年安徽省淮北市七年级(下)期末数学试卷(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 325.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览




文档简介
2020-2021学年安徽省淮北市七年级(下)期末数学试卷
一、选择题(本大题共10小题,共30分)
1.(3分)下列说法不正确的是( )
A.的平方根是±
B.﹣9是81的平方根
C.0.4的算术平方根是0.2
D.=﹣3
2.(3分)下列不等式变形正确的是( )
A.由a>b,得ac>bc
B.由a>b,得a﹣2<b﹣2
C.由﹣>﹣1,得﹣>﹣a
D.由a>b,得c﹣a<c﹣b
3.(3分)某种计算机完成一次基本运算的时间约为1纳秒(ns),已知1纳秒=0.000
000
001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为( )
A.1.5×10﹣9秒
B.15×10﹣9秒
C.1.5×10﹣8秒
D.15×10﹣8秒
4.(3分)下列因式分解正确的是( )
A.(a﹣3)2=a2﹣6a+9
B.﹣4a+a2=﹣a(4+a)
C.a2+4a+4=(a+2)2
D.a2﹣2a+1=a(a﹣2)+1
5.(3分)如果分式的值为0,那么x的值为( )
A.﹣1
B.1
C.﹣1或1
D.1或0
6.(3分)点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离为( )
A.5cm
B.4cm
C.2cm
D.不大于2cm
7.(3分)将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )
A.扩大6倍
B.扩大9倍
C.不变
D.扩大3倍
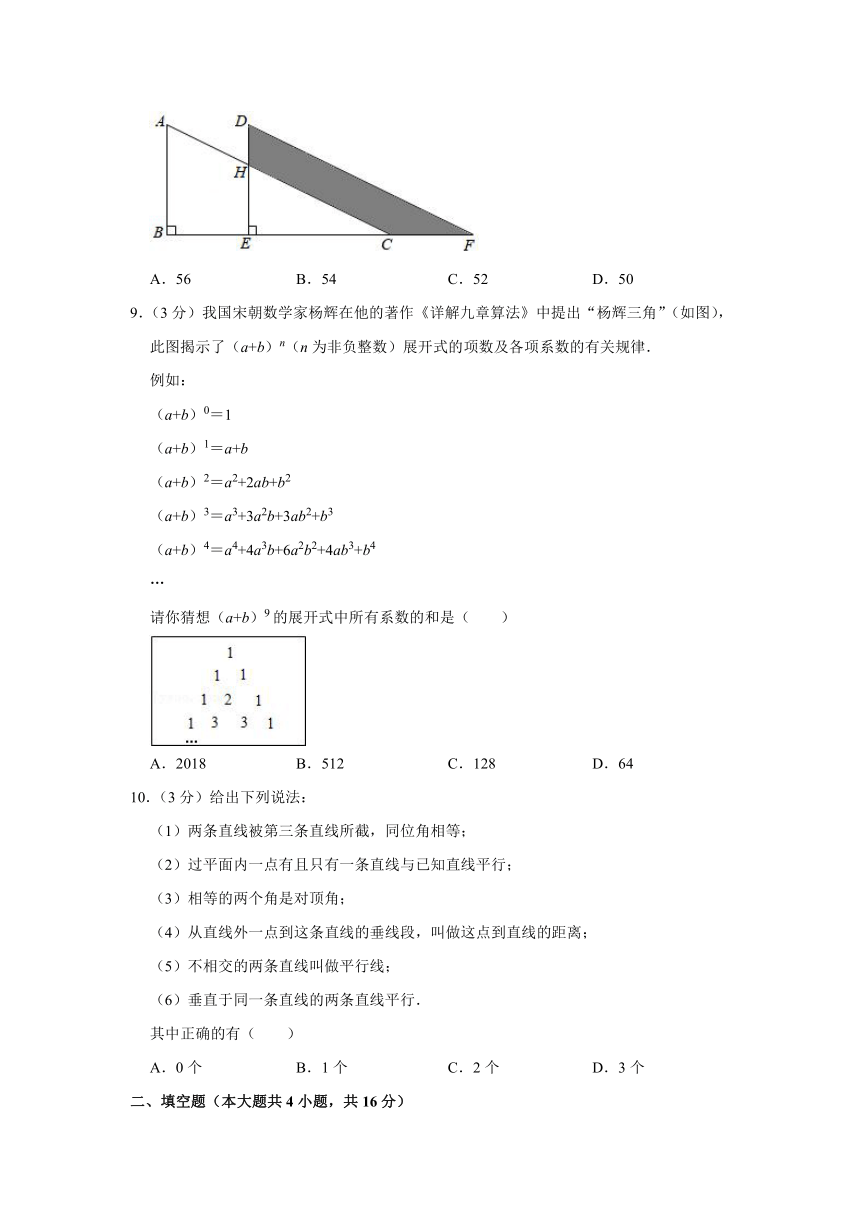
8.(3分)如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=10,DH=4,平移距离为7,求阴影部分的面积为( )
A.56
B.54
C.52
D.50
9.(3分)我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
请你猜想(a+b)9的展开式中所有系数的和是( )
A.2018
B.512
C.128
D.64
10.(3分)给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)过平面内一点有且只有一条直线与已知直线平行;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
(5)不相交的两条直线叫做平行线;
(6)垂直于同一条直线的两条直线平行.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
二、填空题(本大题共4小题,共16分)
11.(3分)若关于x的分式方程﹣1=有增根,则m的值为
.
12.(3分)若9x2+kx+1是一个完全平方式,则k=
.
13.(3分)若+=2,则=
.
14.(3分)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为
.
三、计算题(本大题共4小题,每题8分,共32分)
15.(8分)+(﹣3)2﹣+|﹣2|+()2.
16.(8分)先化简,然后从﹣1≤x≤2的范围内选取一个你喜欢的整数作为x的值代入求值,
17.(8分)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是
;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
18.(8分)已知2m=3,2n=5,求24m﹣2n的值.
四、解答题(本大题共4小题,19,20,21题10分,22题12分,共42分)
19.(10分)阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,事实上,小明的表示方法是有道理的,因为<<,所以的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
(1)的整数部分是
,小数部分是
(2)如果的小数部分为a,的整数部分为b,求a+b﹣的值;
(3)若设2+的整数部分为x,小数部分为y,求y﹣x的值.
20.(10分)完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,(
)
又∵∠A=∠1,(已知)
∴AC∥
,(
)
∴∠2=
,(
)
∴∠C=∠E(等量代换)
21.(10分)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
22.(12分)如图,已知AM∥BN,∠A=80°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.(推理时不需要写出每一步的理由)
(1)求∠CBD的度数.
(2)当点P运动时,那么∠APB与∠ADB的大小关系是否发生变化?若不变,请找出它们的关系并说明理由;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
2020-2021学年安徽省淮北市七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,共30分)
1.(3分)下列说法不正确的是( )
A.的平方根是±
B.﹣9是81的平方根
C.0.4的算术平方根是0.2
D.=﹣3
【分析】根据立方根与平方根的定义即可求出答案.
【解答】解:0.4的算术平方根为,故C错误,
故选:C.
2.(3分)下列不等式变形正确的是( )
A.由a>b,得ac>bc
B.由a>b,得a﹣2<b﹣2
C.由﹣>﹣1,得﹣>﹣a
D.由a>b,得c﹣a<c﹣b
【分析】分别利用不等式的基本性质判断得出即可.
【解答】解:A、由a>b,得ac>bc(c>0),故此选项错误;
B、由a>b,得a﹣2>b﹣2,故此选项错误;
C、由﹣>﹣1,得﹣>﹣a(a>0),故此选项错误;
D、由a>b,得c﹣a<c﹣b,此选项正确.
故选:D.
3.(3分)某种计算机完成一次基本运算的时间约为1纳秒(ns),已知1纳秒=0.000
000
001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为( )
A.1.5×10﹣9秒
B.15×10﹣9秒
C.1.5×10﹣8秒
D.15×10﹣8秒
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:所用时间=15×0.000
000
001=1.5×10﹣8.
故选:C.
4.(3分)下列因式分解正确的是( )
A.(a﹣3)2=a2﹣6a+9
B.﹣4a+a2=﹣a(4+a)
C.a2+4a+4=(a+2)2
D.a2﹣2a+1=a(a﹣2)+1
【分析】直接利用因式分解的定义以及完全平方公式分析得出答案.
【解答】解:A、(a﹣3)2=a2﹣6a+9,是整式的乘法运算,故此选项不合题意;
B、﹣4a+a2=﹣a(4﹣a),故此选项错误;
C、a2+4a+4=(a+2)2,是因式分解,故此选项符合题意;
D、a2﹣2a+1=a(a﹣2)+1,不符合因式分解的定义,故此选项不合题意;
故选:C.
5.(3分)如果分式的值为0,那么x的值为( )
A.﹣1
B.1
C.﹣1或1
D.1或0
【分析】根据分式的值为零的条件可以求出x的值.
【解答】解:根据题意,得
|x|﹣1=0且x+1≠0,
解得,x=1.
故选:B.
6.(3分)点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离为( )
A.5cm
B.4cm
C.2cm
D.不大于2cm
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PC,
即点P到直线l的距离不大于2cm.
故选:D.
7.(3分)将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )
A.扩大6倍
B.扩大9倍
C.不变
D.扩大3倍
【分析】将原式中的x、y分别用3x、3y代替,化简,再与原分式进行比较.
【解答】解:∵把分式中的x与y同时扩大为原来的3倍,
∴原式变为:==9×,
∴这个分式的值扩大9倍.
故选:B.
8.(3分)如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=10,DH=4,平移距离为7,求阴影部分的面积为( )
A.56
B.54
C.52
D.50
【分析】由S△ABC=S△DEF,推出S四边形ABEH=S阴即可解决问题.
【解答】解:∵平移距离为7,
∴BE=7,
∵AB=10,DH=4,
∴EH=10﹣4=6,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴,
∴阴影部分的面积为=×(10+6)×7=56,
故选:A.
9.(3分)我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
请你猜想(a+b)9的展开式中所有系数的和是( )
A.2018
B.512
C.128
D.64
【分析】本题通过阅读理解寻找规律,观察可得(a+b)n(n为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b)n﹣1相邻两项的系数和.
【解答】解:展开式共有n+1项,系数和为2n.
∴(a+b)9的展开式中所有系数的和是:29=512
故选:B.
10.(3分)给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)过平面内一点有且只有一条直线与已知直线平行;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
(5)不相交的两条直线叫做平行线;
(6)垂直于同一条直线的两条直线平行.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
【分析】根据平行线的性质、平行公理、对顶角的概念以及点到直线的距离的概念进行判断即可.
【解答】解:(1)两条直线被第三条直线所截,同位角不一定相等,只有两条平行直线被第三条直线所截,同位角才相等,故说法(1)错误;
(2)过已知直线外一点有且只有一条直线与已知直线平行,说法(2)错误;
(3)相等的两个角不一定是对顶角,对顶角是在两直线相交的前提条件下形成的,故说法(3)错误;
(4)直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,点到直线的距离是一个长度,而不是一个图形,故说法(4)错误;
(5)同一平面内,不相交的两条直线叫做平行线,故说法(5)错误;
(6)同一平面内,垂直于同一条直线的两条直线平行,故说法(6)错误.
故说法正确的有0个.
故选:A.
二、填空题(本大题共4小题,共16分)
11.(3分)若关于x的分式方程﹣1=有增根,则m的值为
3 .
【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x﹣2)=0,得到x=2,然后代入化为整式方程的方程算出m的值.
【解答】解:方程两边都乘(x﹣2),
得3x﹣x+2=m+3
∵原方程有增根,
∴最简公分母(x﹣2)=0,
解得x=2,
当x=2时,m=3.
故答案为3.
12.(3分)若9x2+kx+1是一个完全平方式,则k= ±6 .
【分析】根据完全平方公式可知:(3k±1)2=9x2+kx+1,从而可求出k的值.
【解答】解:∵(3k±1)2=9x2+kx+1,
∴k=±6
故答案为:±6
13.(3分)若+=2,则= .
【分析】根据题意可知x+y=2xy,然后代入原式即可求出答案.
【解答】解:由题意可知:x+y=2xy,
∴原式=
=
=
=,
故答案为:.
14.(3分)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为
45°,60°,105°,135° .
【分析】根据题意画出图形,再由平行线的判定定理即可得出结论.
【解答】解:如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故答案为:45°,60°,105°,135°.
三、计算题(本大题共4小题,每题8分,共32分)
15.(8分)+(﹣3)2﹣+|﹣2|+()2.
【分析】先计算开方、乘方、绝对值的运算,再合并即可得到答案.
【解答】解:原式=
=.
16.(8分)先化简,然后从﹣1≤x≤2的范围内选取一个你喜欢的整数作为x的值代入求值,
【分析】先根据分式的混合运算顺序和运算法则化简原式,再选取使分式有意义的x的值代入计算可得.
【解答】解:原式=?
=,
∵x≠±1,x≠2,
∴可取x=0,
则原式=﹣.
17.(8分)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是
;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
【分析】(1)观察图1与图2,根据两图形阴影部分面积相等验证平方差公式即可;
(2)①已知第一个等式左边利用平方差公式化简,将第二个等式代入求出所求式子的值即可;②原式利用平方差公式变形,约分即可得到结果.
【解答】解:(1)根据图形得:a2﹣b2=(a+b)(a﹣b),
上述操作能验证的等式是B,
故答案为:B;
(2)①∵x2﹣4y2=(x+2y)(x﹣2y)=12,x+2y=4,
∴x﹣2y=3;
②原式=(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)=××××××…××××=×=.
18.(8分)已知2m=3,2n=5,求24m﹣2n的值.
【分析】先把原式化为(2m)4÷(2n)2,再把2m=3,2n=5代入进行计算即可.
【解答】解:∵2m=3,2n=5,
∴原式=(2m)4÷(2n)2=34÷52=.
四、解答题(本大题共4小题,19,20,21题10分,22题12分,共42分)
19.(10分)阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,事实上,小明的表示方法是有道理的,因为<<,所以的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
(1)的整数部分是 3 ,小数部分是 ﹣3
(2)如果的小数部分为a,的整数部分为b,求a+b﹣的值;
(3)若设2+的整数部分为x,小数部分为y,求y﹣x的值.
【分析】根据估算无理数的大小,即可解答.
【解答】解:(1)∵3<<4,
∴的整数部分是3,小数部分是﹣3;
故答案为:3;﹣3.
(2)∵2<<3,
∴a=﹣2,
∵6<<7,
∴b=6,
∴a+b﹣=﹣2+6﹣=4.
(3)∵1<<2,
∴3<2+<4,
∴2+的整数部分为x=3,小数部分为y=2+﹣3=﹣1.
∴y﹣x=﹣4.
20.(10分)完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,( 两直线平行,同位角相等 )
又∵∠A=∠1,(已知)
∴AC∥ DE ,( 内错角相等,两直线平行 )
∴∠2= ∠E ,( 两直线平行,内错角相等 )
∴∠C=∠E(等量代换)
【分析】首先根据平行线的性质求出∠2=∠C,进而求出AC∥DE,即可得到∠2=∠E,利用等量代换得到结论.
【解答】证明:∵BE∥CD,(已知)
∴∠2=∠C,(两直线平行,同位角相等)
又∵∠A=∠1,(已知)
∴AC∥DE,(内错角相等,两直线平行)
∴∠2=∠E,(两直线平行,内错角相等)
∴∠C=∠E(等量代换).
故答案为两直线平行,同位角相等;DE;内错角相等,两直线平行;∠E;两直线平行,内错角相等
21.(10分)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【分析】(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程;
(2)设平均每年绿化面积增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式.
【解答】解:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
﹣=4,
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积增加a万平方米,根据题意得
54×3+2(54+a)≥360,
解得:a≥45.
答:则至少每年平均增加45万平方米.
22.(12分)如图,已知AM∥BN,∠A=80°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.(推理时不需要写出每一步的理由)
(1)求∠CBD的度数.
(2)当点P运动时,那么∠APB与∠ADB的大小关系是否发生变化?若不变,请找出它们的关系并说明理由;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
【分析】(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN=50°+∠DBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=50°,可求得∠ABC的度数.
【解答】解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
一、选择题(本大题共10小题,共30分)
1.(3分)下列说法不正确的是( )
A.的平方根是±
B.﹣9是81的平方根
C.0.4的算术平方根是0.2
D.=﹣3
2.(3分)下列不等式变形正确的是( )
A.由a>b,得ac>bc
B.由a>b,得a﹣2<b﹣2
C.由﹣>﹣1,得﹣>﹣a
D.由a>b,得c﹣a<c﹣b
3.(3分)某种计算机完成一次基本运算的时间约为1纳秒(ns),已知1纳秒=0.000
000
001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为( )
A.1.5×10﹣9秒
B.15×10﹣9秒
C.1.5×10﹣8秒
D.15×10﹣8秒
4.(3分)下列因式分解正确的是( )
A.(a﹣3)2=a2﹣6a+9
B.﹣4a+a2=﹣a(4+a)
C.a2+4a+4=(a+2)2
D.a2﹣2a+1=a(a﹣2)+1
5.(3分)如果分式的值为0,那么x的值为( )
A.﹣1
B.1
C.﹣1或1
D.1或0
6.(3分)点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离为( )
A.5cm
B.4cm
C.2cm
D.不大于2cm
7.(3分)将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )
A.扩大6倍
B.扩大9倍
C.不变
D.扩大3倍
8.(3分)如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=10,DH=4,平移距离为7,求阴影部分的面积为( )
A.56
B.54
C.52
D.50
9.(3分)我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
请你猜想(a+b)9的展开式中所有系数的和是( )
A.2018
B.512
C.128
D.64
10.(3分)给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)过平面内一点有且只有一条直线与已知直线平行;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
(5)不相交的两条直线叫做平行线;
(6)垂直于同一条直线的两条直线平行.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
二、填空题(本大题共4小题,共16分)
11.(3分)若关于x的分式方程﹣1=有增根,则m的值为
.
12.(3分)若9x2+kx+1是一个完全平方式,则k=
.
13.(3分)若+=2,则=
.
14.(3分)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为
.
三、计算题(本大题共4小题,每题8分,共32分)
15.(8分)+(﹣3)2﹣+|﹣2|+()2.
16.(8分)先化简,然后从﹣1≤x≤2的范围内选取一个你喜欢的整数作为x的值代入求值,
17.(8分)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是
;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
18.(8分)已知2m=3,2n=5,求24m﹣2n的值.
四、解答题(本大题共4小题,19,20,21题10分,22题12分,共42分)
19.(10分)阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,事实上,小明的表示方法是有道理的,因为<<,所以的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
(1)的整数部分是
,小数部分是
(2)如果的小数部分为a,的整数部分为b,求a+b﹣的值;
(3)若设2+的整数部分为x,小数部分为y,求y﹣x的值.
20.(10分)完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,(
)
又∵∠A=∠1,(已知)
∴AC∥
,(
)
∴∠2=
,(
)
∴∠C=∠E(等量代换)
21.(10分)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
22.(12分)如图,已知AM∥BN,∠A=80°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.(推理时不需要写出每一步的理由)
(1)求∠CBD的度数.
(2)当点P运动时,那么∠APB与∠ADB的大小关系是否发生变化?若不变,请找出它们的关系并说明理由;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
2020-2021学年安徽省淮北市七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,共30分)
1.(3分)下列说法不正确的是( )
A.的平方根是±
B.﹣9是81的平方根
C.0.4的算术平方根是0.2
D.=﹣3
【分析】根据立方根与平方根的定义即可求出答案.
【解答】解:0.4的算术平方根为,故C错误,
故选:C.
2.(3分)下列不等式变形正确的是( )
A.由a>b,得ac>bc
B.由a>b,得a﹣2<b﹣2
C.由﹣>﹣1,得﹣>﹣a
D.由a>b,得c﹣a<c﹣b
【分析】分别利用不等式的基本性质判断得出即可.
【解答】解:A、由a>b,得ac>bc(c>0),故此选项错误;
B、由a>b,得a﹣2>b﹣2,故此选项错误;
C、由﹣>﹣1,得﹣>﹣a(a>0),故此选项错误;
D、由a>b,得c﹣a<c﹣b,此选项正确.
故选:D.
3.(3分)某种计算机完成一次基本运算的时间约为1纳秒(ns),已知1纳秒=0.000
000
001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为( )
A.1.5×10﹣9秒
B.15×10﹣9秒
C.1.5×10﹣8秒
D.15×10﹣8秒
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:所用时间=15×0.000
000
001=1.5×10﹣8.
故选:C.
4.(3分)下列因式分解正确的是( )
A.(a﹣3)2=a2﹣6a+9
B.﹣4a+a2=﹣a(4+a)
C.a2+4a+4=(a+2)2
D.a2﹣2a+1=a(a﹣2)+1
【分析】直接利用因式分解的定义以及完全平方公式分析得出答案.
【解答】解:A、(a﹣3)2=a2﹣6a+9,是整式的乘法运算,故此选项不合题意;
B、﹣4a+a2=﹣a(4﹣a),故此选项错误;
C、a2+4a+4=(a+2)2,是因式分解,故此选项符合题意;
D、a2﹣2a+1=a(a﹣2)+1,不符合因式分解的定义,故此选项不合题意;
故选:C.
5.(3分)如果分式的值为0,那么x的值为( )
A.﹣1
B.1
C.﹣1或1
D.1或0
【分析】根据分式的值为零的条件可以求出x的值.
【解答】解:根据题意,得
|x|﹣1=0且x+1≠0,
解得,x=1.
故选:B.
6.(3分)点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离为( )
A.5cm
B.4cm
C.2cm
D.不大于2cm
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PC,
即点P到直线l的距离不大于2cm.
故选:D.
7.(3分)将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )
A.扩大6倍
B.扩大9倍
C.不变
D.扩大3倍
【分析】将原式中的x、y分别用3x、3y代替,化简,再与原分式进行比较.
【解答】解:∵把分式中的x与y同时扩大为原来的3倍,
∴原式变为:==9×,
∴这个分式的值扩大9倍.
故选:B.
8.(3分)如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=10,DH=4,平移距离为7,求阴影部分的面积为( )
A.56
B.54
C.52
D.50
【分析】由S△ABC=S△DEF,推出S四边形ABEH=S阴即可解决问题.
【解答】解:∵平移距离为7,
∴BE=7,
∵AB=10,DH=4,
∴EH=10﹣4=6,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴,
∴阴影部分的面积为=×(10+6)×7=56,
故选:A.
9.(3分)我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
请你猜想(a+b)9的展开式中所有系数的和是( )
A.2018
B.512
C.128
D.64
【分析】本题通过阅读理解寻找规律,观察可得(a+b)n(n为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b)n﹣1相邻两项的系数和.
【解答】解:展开式共有n+1项,系数和为2n.
∴(a+b)9的展开式中所有系数的和是:29=512
故选:B.
10.(3分)给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)过平面内一点有且只有一条直线与已知直线平行;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
(5)不相交的两条直线叫做平行线;
(6)垂直于同一条直线的两条直线平行.
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
【分析】根据平行线的性质、平行公理、对顶角的概念以及点到直线的距离的概念进行判断即可.
【解答】解:(1)两条直线被第三条直线所截,同位角不一定相等,只有两条平行直线被第三条直线所截,同位角才相等,故说法(1)错误;
(2)过已知直线外一点有且只有一条直线与已知直线平行,说法(2)错误;
(3)相等的两个角不一定是对顶角,对顶角是在两直线相交的前提条件下形成的,故说法(3)错误;
(4)直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,点到直线的距离是一个长度,而不是一个图形,故说法(4)错误;
(5)同一平面内,不相交的两条直线叫做平行线,故说法(5)错误;
(6)同一平面内,垂直于同一条直线的两条直线平行,故说法(6)错误.
故说法正确的有0个.
故选:A.
二、填空题(本大题共4小题,共16分)
11.(3分)若关于x的分式方程﹣1=有增根,则m的值为
3 .
【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x﹣2)=0,得到x=2,然后代入化为整式方程的方程算出m的值.
【解答】解:方程两边都乘(x﹣2),
得3x﹣x+2=m+3
∵原方程有增根,
∴最简公分母(x﹣2)=0,
解得x=2,
当x=2时,m=3.
故答案为3.
12.(3分)若9x2+kx+1是一个完全平方式,则k= ±6 .
【分析】根据完全平方公式可知:(3k±1)2=9x2+kx+1,从而可求出k的值.
【解答】解:∵(3k±1)2=9x2+kx+1,
∴k=±6
故答案为:±6
13.(3分)若+=2,则= .
【分析】根据题意可知x+y=2xy,然后代入原式即可求出答案.
【解答】解:由题意可知:x+y=2xy,
∴原式=
=
=
=,
故答案为:.
14.(3分)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为
45°,60°,105°,135° .
【分析】根据题意画出图形,再由平行线的判定定理即可得出结论.
【解答】解:如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故答案为:45°,60°,105°,135°.
三、计算题(本大题共4小题,每题8分,共32分)
15.(8分)+(﹣3)2﹣+|﹣2|+()2.
【分析】先计算开方、乘方、绝对值的运算,再合并即可得到答案.
【解答】解:原式=
=.
16.(8分)先化简,然后从﹣1≤x≤2的范围内选取一个你喜欢的整数作为x的值代入求值,
【分析】先根据分式的混合运算顺序和运算法则化简原式,再选取使分式有意义的x的值代入计算可得.
【解答】解:原式=?
=,
∵x≠±1,x≠2,
∴可取x=0,
则原式=﹣.
17.(8分)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是
;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
【分析】(1)观察图1与图2,根据两图形阴影部分面积相等验证平方差公式即可;
(2)①已知第一个等式左边利用平方差公式化简,将第二个等式代入求出所求式子的值即可;②原式利用平方差公式变形,约分即可得到结果.
【解答】解:(1)根据图形得:a2﹣b2=(a+b)(a﹣b),
上述操作能验证的等式是B,
故答案为:B;
(2)①∵x2﹣4y2=(x+2y)(x﹣2y)=12,x+2y=4,
∴x﹣2y=3;
②原式=(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)=××××××…××××=×=.
18.(8分)已知2m=3,2n=5,求24m﹣2n的值.
【分析】先把原式化为(2m)4÷(2n)2,再把2m=3,2n=5代入进行计算即可.
【解答】解:∵2m=3,2n=5,
∴原式=(2m)4÷(2n)2=34÷52=.
四、解答题(本大题共4小题,19,20,21题10分,22题12分,共42分)
19.(10分)阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用﹣1来表示的小数部分,事实上,小明的表示方法是有道理的,因为<<,所以的整数部分是1,将这个数减去其整数部分,差就是小数部分.请据此解答:
(1)的整数部分是 3 ,小数部分是 ﹣3
(2)如果的小数部分为a,的整数部分为b,求a+b﹣的值;
(3)若设2+的整数部分为x,小数部分为y,求y﹣x的值.
【分析】根据估算无理数的大小,即可解答.
【解答】解:(1)∵3<<4,
∴的整数部分是3,小数部分是﹣3;
故答案为:3;﹣3.
(2)∵2<<3,
∴a=﹣2,
∵6<<7,
∴b=6,
∴a+b﹣=﹣2+6﹣=4.
(3)∵1<<2,
∴3<2+<4,
∴2+的整数部分为x=3,小数部分为y=2+﹣3=﹣1.
∴y﹣x=﹣4.
20.(10分)完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,( 两直线平行,同位角相等 )
又∵∠A=∠1,(已知)
∴AC∥ DE ,( 内错角相等,两直线平行 )
∴∠2= ∠E ,( 两直线平行,内错角相等 )
∴∠C=∠E(等量代换)
【分析】首先根据平行线的性质求出∠2=∠C,进而求出AC∥DE,即可得到∠2=∠E,利用等量代换得到结论.
【解答】证明:∵BE∥CD,(已知)
∴∠2=∠C,(两直线平行,同位角相等)
又∵∠A=∠1,(已知)
∴AC∥DE,(内错角相等,两直线平行)
∴∠2=∠E,(两直线平行,内错角相等)
∴∠C=∠E(等量代换).
故答案为两直线平行,同位角相等;DE;内错角相等,两直线平行;∠E;两直线平行,内错角相等
21.(10分)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【分析】(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程;
(2)设平均每年绿化面积增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式.
【解答】解:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
﹣=4,
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积增加a万平方米,根据题意得
54×3+2(54+a)≥360,
解得:a≥45.
答:则至少每年平均增加45万平方米.
22.(12分)如图,已知AM∥BN,∠A=80°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.(推理时不需要写出每一步的理由)
(1)求∠CBD的度数.
(2)当点P运动时,那么∠APB与∠ADB的大小关系是否发生变化?若不变,请找出它们的关系并说明理由;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
【分析】(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN=50°+∠DBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=50°,可求得∠ABC的度数.
【解答】解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
同课章节目录
