2020-2021学年湖南省常德市四校联考八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省常德市四校联考八年级(上)期中数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 343.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览




文档简介
2020-2021学年湖南省常德市四校联考八年级(上)期中数学试卷
一、选择题(每题3分,共24分)
1.(3分)下列分式中是最简分式的是( )
A. B. C. D.
2.(3分)以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
3.(3分)如果将分式中的字母x与y的值分别扩大为原来的10倍,那么这个分式的值( )
A.扩大为原来的10倍 B.扩大为原来的20倍
C.缩小为原来的 D.不改变
4.(3分)用反证法证明命题“一个三角形中不能有两个角是钝角”,应先假设这个三角形中( )
A.有两个角是直角
B.有两个角是钝角
C.有两个角是锐角
D.一个角是钝角,一个角是直角
5.(3分)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF
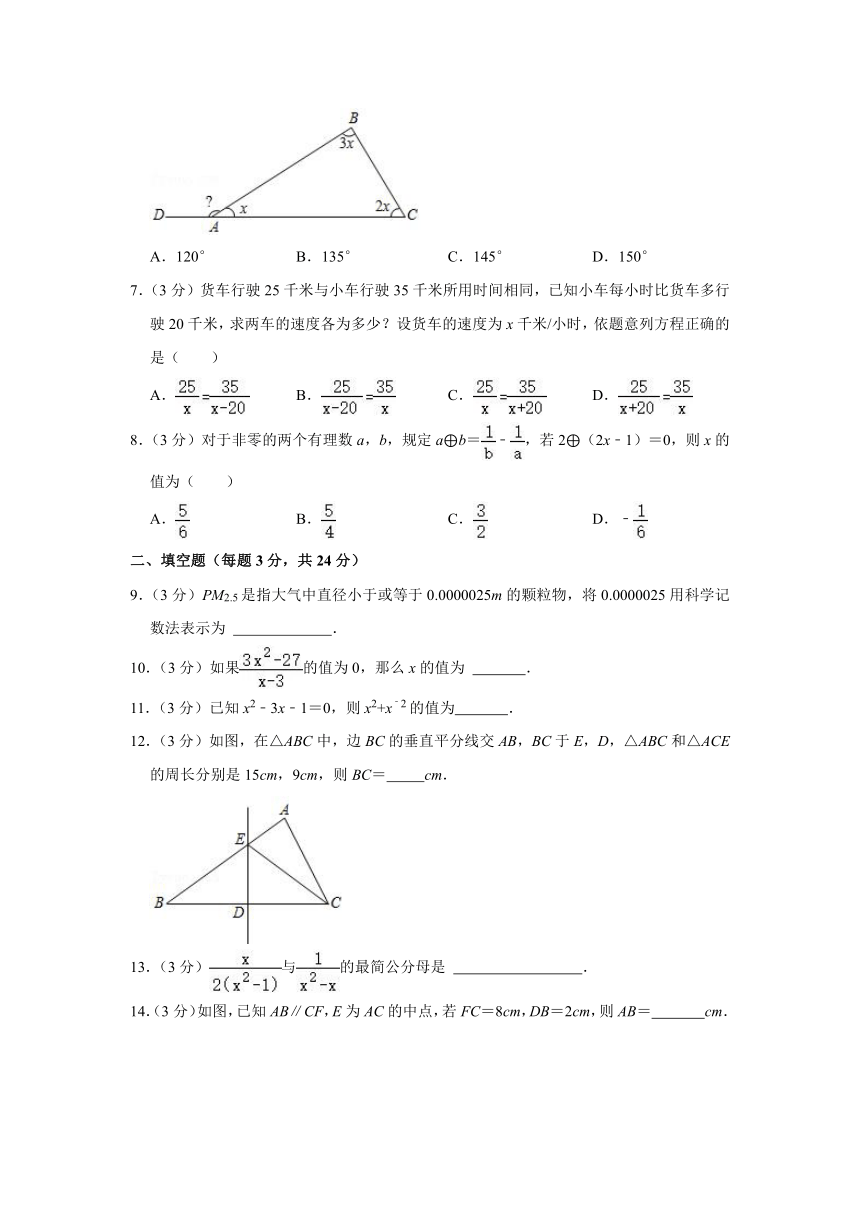
6.(3分)在△ABC中,∠BAC=x,∠B=3x,∠C=2x,则∠BAD=( )
A.120° B.135° C.145° D.150°
7.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
8.(3分)对于非零的两个有理数a,b,规定a⊕b=﹣,若2⊕(2x﹣1)=0,则x的值为( )
A. B. C. D.﹣
二、填空题(每题3分,共24分)
9.(3分)PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .
10.(3分)如果的值为0,那么x的值为 .
11.(3分)已知x2﹣3x﹣1=0,则x2+x﹣2的值为 .
12.(3分)如图,在△ABC中,边BC的垂直平分线交AB,BC于E,D,△ABC和△ACE的周长分别是15cm,9cm,则BC= cm.
13.(3分)与的最简公分母是 .
14.(3分)如图,已知AB∥CF,E为AC的中点,若FC=8cm,DB=2cm,则AB= cm.
15.(3分)若am=3,an=2,则am﹣2n的值为 .
16.(3分)如图,在△ABC中,∠A=x°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…,∠An﹣1BC和∠An﹣1CD的平分线交于点An,则∠An= .
三、解答题(共72分)
17.(8分)计算:
(1)÷+;
(2)()﹣2+(3.14﹣π)0﹣|﹣2|.
18.(8分)解方程
(1)=1﹣;
(2)+=1.
19.(5分)先化简,再求值:(),其中x=2.
20.(5分)如图,等边△ABC中,D、E分别为AC、AB上两点,DE∥BC,求证:△ADE是等边三角形.
21.(6分)如图,在△ABC中,∠A=50°,∠C=65°,AB=13,BC=11,DE垂直平分AB交AC、AB于E、D两点.求:
(1)∠EBC的度数;
(2)△BCE的周长.
22.(6分)已知关于x的方程无解,求a的值.
23.(7分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,AD=9cm,BE=4cm,求DE的长.
24.(7分)某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
25.(10分)阅读下列解题过程,并完成问题:
若=﹣2,求的值.
解:因为=﹣2,所以a=﹣2b.
所以===.
(1)解题过程中,由得,是对分式进行了 ;
(2)已知=,求的值;
(3)已知==≠0,求的值.
26.(10分)已知:如图1,△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到点A,使DA=DF,延长BF交AC于点E.
(1)求证:△BDF≌△CDA;
(2)试说明:△ABC是等腰三角形;
(3)连接AF并延长,交BC于点G,如图2,求证:AG⊥BC.
2020-2021学年湖南省常德市四校联考八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题3分,共24分)
1.(3分)下列分式中是最简分式的是( )
A. B. C. D.
【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
【解答】解:A、的分子、分母都不能再分解,且不能约分,是最简分式;
B、;
C、=;
D、;
故选:A.
2.(3分)以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选:B.
3.(3分)如果将分式中的字母x与y的值分别扩大为原来的10倍,那么这个分式的值( )
A.扩大为原来的10倍 B.扩大为原来的20倍
C.缩小为原来的 D.不改变
【分析】先根据题意列出算式,再根据分式的基本性质进行化简即可.
【解答】解:
=
=,
即分式的值不变,
故选:D.
4.(3分)用反证法证明命题“一个三角形中不能有两个角是钝角”,应先假设这个三角形中( )
A.有两个角是直角
B.有两个角是钝角
C.有两个角是锐角
D.一个角是钝角,一个角是直角
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解答】解:用反证法证明命题“一个三角形中不能有两个角是钝角”,
应先假设这个三角形有两个角是钝角,
故选:B.
5.(3分)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF
【分析】根据全等三角形的判定,利用ASA、SAS、AAS即可得答案.
【解答】解:∵∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;
∴添加BC=EF,利用SAS可得△ABC≌△DEF;
∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;
故选:D.
6.(3分)在△ABC中,∠BAC=x,∠B=3x,∠C=2x,则∠BAD=( )
A.120° B.135° C.145° D.150°
【分析】根据三角形内角和定理求出x,再求出答案即可.
【解答】解:∵∠B+∠BAC+∠C=180°,
又∵∠BAC=x,∠B=3x,∠C=2x,
∴6x=180°,
解得:x=30°,
即∠BAC=30°
∴∠BAD=180°﹣∠BAC=150°,
故选:D.
7.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.
【解答】解:根据题意,得
.
故选:C.
8.(3分)对于非零的两个有理数a,b,规定a⊕b=﹣,若2⊕(2x﹣1)=0,则x的值为( )
A. B. C. D.﹣
【分析】已知等式利用题中的新定义化简,计算即可求出x的值.
【解答】解:根据题中的新定义化简2⊕(2x﹣1)=0得:﹣=0,
去分母得:2﹣2x+1=0,
解得:x=,
检验:把x=代入得:2x﹣1≠0,
∴分式方程的解为x=.
故选:C.
二、填空题(每题3分,共24分)
9.(3分)PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 2.5×10﹣6 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.0000025=2.5×10﹣6,
故答案为:2.5×10﹣6.
10.(3分)如果的值为0,那么x的值为 ﹣3 .
【分析】分式的值为零,分子等于0,分母不为0.
【解答】解:根据题意,得
,
解得x=﹣3.
故答案是:﹣3.
11.(3分)已知x2﹣3x﹣1=0,则x2+x﹣2的值为 11 .
【分析】已知等式两边除以x变形后,两边平方,利用完全平方公式变形即可求出所求式子的值.
【解答】解:∵x≠0,
∴已知等式变形得:x﹣=3,
两边平方得:(x﹣)2=x2+x﹣2﹣2=3,
则x2+x﹣2=(x﹣)2+2=11,
故答案为:11
12.(3分)如图,在△ABC中,边BC的垂直平分线交AB,BC于E,D,△ABC和△ACE的周长分别是15cm,9cm,则BC= 6 cm.
【分析】根据线段垂直平分线的性质得到EB=EC,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是线段BC的垂直平分线,
∴EB=EC,
∵△ABC和△ACE的周长分别是15cm,9cm,
∴AB+AC+BC=15cm,AC+AE+EC=AC+AE+EB=AC+AB=9cm,
∴BC=15﹣9=6(cm),
故答案为:6.
13.(3分)与的最简公分母是 2x(x+1)(x﹣1) .
【分析】确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
【解答】解:分式与的分母分别为:2(x2﹣1)=2(x+1)(x﹣1),x2﹣x=x(x﹣1),则与的最简公分母是2x(x+1)(x﹣1).
故答案是:2x(x+1)(x﹣1).
14.(3分)如图,已知AB∥CF,E为AC的中点,若FC=8cm,DB=2cm,则AB= 10 cm.
【分析】根据平行线的性质求得内错角相等,已知对顶角相等,又知E是AC的中点,所以根据AAS得出△ADE≌△CFE,从而得出AD=FC,已知FC,DB的长,那么AB的长就不难求出.
【解答】解:∵AB∥CF,
∴∠ADE=∠F,
∵E是AC的中点,
∴AE=CE,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=FC,
∵FC=8cm,
∴AD=8cm,
∵DB=2cm,
∴AB=AD+DB=10cm,
故答案为:10.
15.(3分)若am=3,an=2,则am﹣2n的值为 .
【分析】根据同底数幂的除法法则和幂的乘方的运算法则求解.
【解答】解:am﹣2n=3÷4=.
故答案为:.
16.(3分)如图,在△ABC中,∠A=x°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…,∠An﹣1BC和∠An﹣1CD的平分线交于点An,则∠An= .
【分析】根据角平分线的定义得出∠A1BC=ABC,∠A1CD=ACD,根据三角形的外角性质得出∠A1CD=∠A1+∠A1BC,∠ACD=∠A+∠ABC,求出∠A1=A,再求出∠A2,∠A3,再根据求出的结果得出答案即可.
【解答】解:∵∠ABC和∠ACD的平分线交于点A1,
∴∠A1BC=ABC,∠A1CD=ACD,
∵∠A1CD=∠A1+∠A1BC,∠ACD=∠A+∠ABC,
∴∠A1CD=ACD=∠A1+∠A1BC=∠A1+ABC,∠ACD=A+ABC,
∴∠A1=A,
∵∠A=x°,
∴∠A1=x°,
同理:∠A2=A1=×x°=,∠A3=∠A2=,
???,
∠An=∠An﹣1=,
故答案为:.
三、解答题(共72分)
17.(8分)计算:
(1)÷+;
(2)()﹣2+(3.14﹣π)0﹣|﹣2|.
【分析】(1)先因式分解,再将除法转化为乘法,继而约分,最后计算加法即可;
(2)先计算负整数指数幂、零指数幂和绝对值,再计算加减即可.
【解答】解:(1)原式=÷+
=?+
=+
=
=1;
(2)原式=9+1﹣2
=8.
18.(8分)解方程
(1)=1﹣;
(2)+=1.
【分析】(1)分式方程去分母转化为整式方程,求出整式方程得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)去分母得:1﹣x=x﹣2﹣3,
解得:x=3,
检验:把x=3代入得:x﹣2=3﹣2=1≠0,
∴分式方程的解为x=3;
(2)去分母得:(x+1)2﹣4=x2﹣1,
解得:x=1,
检验:把x=1代入得:x﹣1=0,
∴x=1是增根,分式方程无解.
19.(5分)先化简,再求值:(),其中x=2.
【分析】先算括号里面的,再算除法,最后把x的值代入进行计算即可.
【解答】解:原式=[+]÷[﹣]
=÷
=÷
=?
=,
当x=2时,原式==.
20.(5分)如图,等边△ABC中,D、E分别为AC、AB上两点,DE∥BC,求证:△ADE是等边三角形.
【分析】根据等边三角形的性质由△ABC为等边三角形得到∠A=60°,由DE∥BC得到∠ADE=∠C=∠B=∠AED=60°,然后根据等边三角形的判定方法得到△ADE是等边三角形.
【解答】解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠C,∠AED=∠B,
∴∠ADE=∠C=∠B=∠AED=60°,
∴△ADE是等边三角形.
21.(6分)如图,在△ABC中,∠A=50°,∠C=65°,AB=13,BC=11,DE垂直平分AB交AC、AB于E、D两点.求:
(1)∠EBC的度数;
(2)△BCE的周长.
【分析】(1)根据三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到EA=EB,进而得出∠ABE=∠A=50°,计算即可;
(2)根据等腰三角形的判定定理得到AC=AB=13,根据三角形的周长公式计算,得到答案.
【解答】解:(1)在△ABC中,∠A=50°,∠C=65°,
则∠ABC=180°﹣∠A﹣∠C=65°,
∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠ABE=∠A=50°,
∴∠EBC=∠ABC﹣∠ABE=15°;
(2)∵∠ABC=∠C=65°,
∴AC=AB=13,
∴△BCE的周长=BC+CE+EB=BC+CE+EA=BC+AC=24.
22.(6分)已知关于x的方程无解,求a的值.
【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
【解答】解:去分母,整理得(a+1)x=2a+4,①
由于原方程无解,故有以下两种情况:
(1)方程①无实数根,即a+1=0,
而2a+4≠0,此时a=﹣1.
(2)方程①的根x=是增根,则=3,解得a=1.
因此,a的值为﹣1或1.
23.(7分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,AD=9cm,BE=4cm,求DE的长.
【分析】根据垂直的定义及直角三角形的两锐角互余得出∠CAD=∠BCE,即可证明△CDA≌△BEC,可得CD=BE,CE=AD,根据DE=CE﹣CD,即可解题.
【解答】解:∵∠ACB=90°,BE⊥CE于点E,AD⊥CE于点D,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△CDA和△BEC中,
,
∴△CDA≌△BEC(AAS),
∴CD=BE,CE=AD,
∵DE=CE﹣CD,
∴DE=AD﹣BE,
∵AD=9cm,BE=4cm,
∴DE=9cm﹣4cm=5cm.
24.(7分)某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
【分析】(1)设原计划每天修建道路x米,则实际每天修建道路1.5x米,根据题意,列方程解答即可;
(2)由(1)的结论列出方程解答即可.
【解答】解:(1)设原计划每天修建道路x米,
可得:,
解得:x=100,
经检验x=100是原方程的解,
答:原计划每天修建道路100米;
(2)设实际平均每天修建道路的工效比原计划增加y%,
可得:,
解得:y=20,
经检验y=20是原方程的解,
答:实际平均每天修建道路的工效比原计划增加百分之二十.
25.(10分)阅读下列解题过程,并完成问题:
若=﹣2,求的值.
解:因为=﹣2,所以a=﹣2b.
所以===.
(1)解题过程中,由得,是对分式进行了 约分 ;
(2)已知=,求的值;
(3)已知==≠0,求的值.
【分析】(1)根据分式的分子、分母都除以b2,知道是对分式进行了约分;
(2)根据条件得:b=2a,代入代数式中,约去a2即可得到答案;
(3)设=k(k≠0),则x=3k,y=4k,z=5k,代入代数式中,约去k,即可得到答案.
【解答】解:(1)分式的分子、分母都除以b2,
故答案为:约分;
(2)∵=,
∴b=2a,
∴原式=
=
=;
(3)设=k(k≠0),
则x=3k,y=4k,z=5k,
∴原式=
=
=.
26.(10分)已知:如图1,△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到点A,使DA=DF,延长BF交AC于点E.
(1)求证:△BDF≌△CDA;
(2)试说明:△ABC是等腰三角形;
(3)连接AF并延长,交BC于点G,如图2,求证:AG⊥BC.
【分析】(1)由SAS证明△FBD≌△ACD即可;
(2)由全等三角形的性质得∠DBF=∠DCA,再证△ABE≌△CBE(ASA),得AB=CB,即可得出结论;
(3)由全等三角形的性质得AD=DF,DB=DC,则∠DAF=∠DFA=45°,再由等腰直角三角形的性质得∠DCB=45°,然后证∠FGC=90°,即可得出结论.
【解答】证明:(1)∵∠BDC=90°,
∴∠CDA=90°=∠BDF,BD=CD,
又∵DF=DA,
∴△FBD≌△ACD(SAS);
(2)由(1)得:△FBD≌△ACD,
∴∠DBF=∠DCA,
∵∠CDA=90°,
∴∠DAC+∠A=90°,
∴∠DBF+∠A=90°,
∴∠AEB=180°﹣(∠DBF+∠A)=90°,
∴∠CEB=90°=∠AEB,
∵BF平分∠DBC,
∴∠ABF=∠CBF,
又∵BE=BE,
∴△ABE≌△CBE(ASA),
∴AB=CB,
∴△ABC是等腰三角形;
(3)由(1)得:△FBD≌△ACD,
∴AD=DF,DB=DC,
∵∠ADF=90°,
∴∠DAF=∠DFA=45°,
∵△DBC是等腰直角三角形,∠BDC=90°,
∴∠DCB=45°,
∵∠GFC=∠DFA=45°,
∴∠FGC=180°﹣45°﹣45°=90°,
∴AG⊥BC.
一、选择题(每题3分,共24分)
1.(3分)下列分式中是最简分式的是( )
A. B. C. D.
2.(3分)以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
3.(3分)如果将分式中的字母x与y的值分别扩大为原来的10倍,那么这个分式的值( )
A.扩大为原来的10倍 B.扩大为原来的20倍
C.缩小为原来的 D.不改变
4.(3分)用反证法证明命题“一个三角形中不能有两个角是钝角”,应先假设这个三角形中( )
A.有两个角是直角
B.有两个角是钝角
C.有两个角是锐角
D.一个角是钝角,一个角是直角
5.(3分)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF
6.(3分)在△ABC中,∠BAC=x,∠B=3x,∠C=2x,则∠BAD=( )
A.120° B.135° C.145° D.150°
7.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
8.(3分)对于非零的两个有理数a,b,规定a⊕b=﹣,若2⊕(2x﹣1)=0,则x的值为( )
A. B. C. D.﹣
二、填空题(每题3分,共24分)
9.(3分)PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .
10.(3分)如果的值为0,那么x的值为 .
11.(3分)已知x2﹣3x﹣1=0,则x2+x﹣2的值为 .
12.(3分)如图,在△ABC中,边BC的垂直平分线交AB,BC于E,D,△ABC和△ACE的周长分别是15cm,9cm,则BC= cm.
13.(3分)与的最简公分母是 .
14.(3分)如图,已知AB∥CF,E为AC的中点,若FC=8cm,DB=2cm,则AB= cm.
15.(3分)若am=3,an=2,则am﹣2n的值为 .
16.(3分)如图,在△ABC中,∠A=x°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…,∠An﹣1BC和∠An﹣1CD的平分线交于点An,则∠An= .
三、解答题(共72分)
17.(8分)计算:
(1)÷+;
(2)()﹣2+(3.14﹣π)0﹣|﹣2|.
18.(8分)解方程
(1)=1﹣;
(2)+=1.
19.(5分)先化简,再求值:(),其中x=2.
20.(5分)如图,等边△ABC中,D、E分别为AC、AB上两点,DE∥BC,求证:△ADE是等边三角形.
21.(6分)如图,在△ABC中,∠A=50°,∠C=65°,AB=13,BC=11,DE垂直平分AB交AC、AB于E、D两点.求:
(1)∠EBC的度数;
(2)△BCE的周长.
22.(6分)已知关于x的方程无解,求a的值.
23.(7分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,AD=9cm,BE=4cm,求DE的长.
24.(7分)某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
25.(10分)阅读下列解题过程,并完成问题:
若=﹣2,求的值.
解:因为=﹣2,所以a=﹣2b.
所以===.
(1)解题过程中,由得,是对分式进行了 ;
(2)已知=,求的值;
(3)已知==≠0,求的值.
26.(10分)已知:如图1,△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到点A,使DA=DF,延长BF交AC于点E.
(1)求证:△BDF≌△CDA;
(2)试说明:△ABC是等腰三角形;
(3)连接AF并延长,交BC于点G,如图2,求证:AG⊥BC.
2020-2021学年湖南省常德市四校联考八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题3分,共24分)
1.(3分)下列分式中是最简分式的是( )
A. B. C. D.
【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
【解答】解:A、的分子、分母都不能再分解,且不能约分,是最简分式;
B、;
C、=;
D、;
故选:A.
2.(3分)以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选:B.
3.(3分)如果将分式中的字母x与y的值分别扩大为原来的10倍,那么这个分式的值( )
A.扩大为原来的10倍 B.扩大为原来的20倍
C.缩小为原来的 D.不改变
【分析】先根据题意列出算式,再根据分式的基本性质进行化简即可.
【解答】解:
=
=,
即分式的值不变,
故选:D.
4.(3分)用反证法证明命题“一个三角形中不能有两个角是钝角”,应先假设这个三角形中( )
A.有两个角是直角
B.有两个角是钝角
C.有两个角是锐角
D.一个角是钝角,一个角是直角
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解答】解:用反证法证明命题“一个三角形中不能有两个角是钝角”,
应先假设这个三角形有两个角是钝角,
故选:B.
5.(3分)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF
【分析】根据全等三角形的判定,利用ASA、SAS、AAS即可得答案.
【解答】解:∵∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;
∴添加BC=EF,利用SAS可得△ABC≌△DEF;
∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;
故选:D.
6.(3分)在△ABC中,∠BAC=x,∠B=3x,∠C=2x,则∠BAD=( )
A.120° B.135° C.145° D.150°
【分析】根据三角形内角和定理求出x,再求出答案即可.
【解答】解:∵∠B+∠BAC+∠C=180°,
又∵∠BAC=x,∠B=3x,∠C=2x,
∴6x=180°,
解得:x=30°,
即∠BAC=30°
∴∠BAD=180°﹣∠BAC=150°,
故选:D.
7.(3分)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A. B. C. D.
【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.
【解答】解:根据题意,得
.
故选:C.
8.(3分)对于非零的两个有理数a,b,规定a⊕b=﹣,若2⊕(2x﹣1)=0,则x的值为( )
A. B. C. D.﹣
【分析】已知等式利用题中的新定义化简,计算即可求出x的值.
【解答】解:根据题中的新定义化简2⊕(2x﹣1)=0得:﹣=0,
去分母得:2﹣2x+1=0,
解得:x=,
检验:把x=代入得:2x﹣1≠0,
∴分式方程的解为x=.
故选:C.
二、填空题(每题3分,共24分)
9.(3分)PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 2.5×10﹣6 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.0000025=2.5×10﹣6,
故答案为:2.5×10﹣6.
10.(3分)如果的值为0,那么x的值为 ﹣3 .
【分析】分式的值为零,分子等于0,分母不为0.
【解答】解:根据题意,得
,
解得x=﹣3.
故答案是:﹣3.
11.(3分)已知x2﹣3x﹣1=0,则x2+x﹣2的值为 11 .
【分析】已知等式两边除以x变形后,两边平方,利用完全平方公式变形即可求出所求式子的值.
【解答】解:∵x≠0,
∴已知等式变形得:x﹣=3,
两边平方得:(x﹣)2=x2+x﹣2﹣2=3,
则x2+x﹣2=(x﹣)2+2=11,
故答案为:11
12.(3分)如图,在△ABC中,边BC的垂直平分线交AB,BC于E,D,△ABC和△ACE的周长分别是15cm,9cm,则BC= 6 cm.
【分析】根据线段垂直平分线的性质得到EB=EC,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是线段BC的垂直平分线,
∴EB=EC,
∵△ABC和△ACE的周长分别是15cm,9cm,
∴AB+AC+BC=15cm,AC+AE+EC=AC+AE+EB=AC+AB=9cm,
∴BC=15﹣9=6(cm),
故答案为:6.
13.(3分)与的最简公分母是 2x(x+1)(x﹣1) .
【分析】确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
【解答】解:分式与的分母分别为:2(x2﹣1)=2(x+1)(x﹣1),x2﹣x=x(x﹣1),则与的最简公分母是2x(x+1)(x﹣1).
故答案是:2x(x+1)(x﹣1).
14.(3分)如图,已知AB∥CF,E为AC的中点,若FC=8cm,DB=2cm,则AB= 10 cm.
【分析】根据平行线的性质求得内错角相等,已知对顶角相等,又知E是AC的中点,所以根据AAS得出△ADE≌△CFE,从而得出AD=FC,已知FC,DB的长,那么AB的长就不难求出.
【解答】解:∵AB∥CF,
∴∠ADE=∠F,
∵E是AC的中点,
∴AE=CE,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=FC,
∵FC=8cm,
∴AD=8cm,
∵DB=2cm,
∴AB=AD+DB=10cm,
故答案为:10.
15.(3分)若am=3,an=2,则am﹣2n的值为 .
【分析】根据同底数幂的除法法则和幂的乘方的运算法则求解.
【解答】解:am﹣2n=3÷4=.
故答案为:.
16.(3分)如图,在△ABC中,∠A=x°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…,∠An﹣1BC和∠An﹣1CD的平分线交于点An,则∠An= .
【分析】根据角平分线的定义得出∠A1BC=ABC,∠A1CD=ACD,根据三角形的外角性质得出∠A1CD=∠A1+∠A1BC,∠ACD=∠A+∠ABC,求出∠A1=A,再求出∠A2,∠A3,再根据求出的结果得出答案即可.
【解答】解:∵∠ABC和∠ACD的平分线交于点A1,
∴∠A1BC=ABC,∠A1CD=ACD,
∵∠A1CD=∠A1+∠A1BC,∠ACD=∠A+∠ABC,
∴∠A1CD=ACD=∠A1+∠A1BC=∠A1+ABC,∠ACD=A+ABC,
∴∠A1=A,
∵∠A=x°,
∴∠A1=x°,
同理:∠A2=A1=×x°=,∠A3=∠A2=,
???,
∠An=∠An﹣1=,
故答案为:.
三、解答题(共72分)
17.(8分)计算:
(1)÷+;
(2)()﹣2+(3.14﹣π)0﹣|﹣2|.
【分析】(1)先因式分解,再将除法转化为乘法,继而约分,最后计算加法即可;
(2)先计算负整数指数幂、零指数幂和绝对值,再计算加减即可.
【解答】解:(1)原式=÷+
=?+
=+
=
=1;
(2)原式=9+1﹣2
=8.
18.(8分)解方程
(1)=1﹣;
(2)+=1.
【分析】(1)分式方程去分母转化为整式方程,求出整式方程得到x的值,经检验即可得到分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程得到x的值,经检验即可得到分式方程的解.
【解答】解:(1)去分母得:1﹣x=x﹣2﹣3,
解得:x=3,
检验:把x=3代入得:x﹣2=3﹣2=1≠0,
∴分式方程的解为x=3;
(2)去分母得:(x+1)2﹣4=x2﹣1,
解得:x=1,
检验:把x=1代入得:x﹣1=0,
∴x=1是增根,分式方程无解.
19.(5分)先化简,再求值:(),其中x=2.
【分析】先算括号里面的,再算除法,最后把x的值代入进行计算即可.
【解答】解:原式=[+]÷[﹣]
=÷
=÷
=?
=,
当x=2时,原式==.
20.(5分)如图,等边△ABC中,D、E分别为AC、AB上两点,DE∥BC,求证:△ADE是等边三角形.
【分析】根据等边三角形的性质由△ABC为等边三角形得到∠A=60°,由DE∥BC得到∠ADE=∠C=∠B=∠AED=60°,然后根据等边三角形的判定方法得到△ADE是等边三角形.
【解答】解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠C,∠AED=∠B,
∴∠ADE=∠C=∠B=∠AED=60°,
∴△ADE是等边三角形.
21.(6分)如图,在△ABC中,∠A=50°,∠C=65°,AB=13,BC=11,DE垂直平分AB交AC、AB于E、D两点.求:
(1)∠EBC的度数;
(2)△BCE的周长.
【分析】(1)根据三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到EA=EB,进而得出∠ABE=∠A=50°,计算即可;
(2)根据等腰三角形的判定定理得到AC=AB=13,根据三角形的周长公式计算,得到答案.
【解答】解:(1)在△ABC中,∠A=50°,∠C=65°,
则∠ABC=180°﹣∠A﹣∠C=65°,
∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠ABE=∠A=50°,
∴∠EBC=∠ABC﹣∠ABE=15°;
(2)∵∠ABC=∠C=65°,
∴AC=AB=13,
∴△BCE的周长=BC+CE+EB=BC+CE+EA=BC+AC=24.
22.(6分)已知关于x的方程无解,求a的值.
【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
【解答】解:去分母,整理得(a+1)x=2a+4,①
由于原方程无解,故有以下两种情况:
(1)方程①无实数根,即a+1=0,
而2a+4≠0,此时a=﹣1.
(2)方程①的根x=是增根,则=3,解得a=1.
因此,a的值为﹣1或1.
23.(7分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,AD=9cm,BE=4cm,求DE的长.
【分析】根据垂直的定义及直角三角形的两锐角互余得出∠CAD=∠BCE,即可证明△CDA≌△BEC,可得CD=BE,CE=AD,根据DE=CE﹣CD,即可解题.
【解答】解:∵∠ACB=90°,BE⊥CE于点E,AD⊥CE于点D,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△CDA和△BEC中,
,
∴△CDA≌△BEC(AAS),
∴CD=BE,CE=AD,
∵DE=CE﹣CD,
∴DE=AD﹣BE,
∵AD=9cm,BE=4cm,
∴DE=9cm﹣4cm=5cm.
24.(7分)某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
【分析】(1)设原计划每天修建道路x米,则实际每天修建道路1.5x米,根据题意,列方程解答即可;
(2)由(1)的结论列出方程解答即可.
【解答】解:(1)设原计划每天修建道路x米,
可得:,
解得:x=100,
经检验x=100是原方程的解,
答:原计划每天修建道路100米;
(2)设实际平均每天修建道路的工效比原计划增加y%,
可得:,
解得:y=20,
经检验y=20是原方程的解,
答:实际平均每天修建道路的工效比原计划增加百分之二十.
25.(10分)阅读下列解题过程,并完成问题:
若=﹣2,求的值.
解:因为=﹣2,所以a=﹣2b.
所以===.
(1)解题过程中,由得,是对分式进行了 约分 ;
(2)已知=,求的值;
(3)已知==≠0,求的值.
【分析】(1)根据分式的分子、分母都除以b2,知道是对分式进行了约分;
(2)根据条件得:b=2a,代入代数式中,约去a2即可得到答案;
(3)设=k(k≠0),则x=3k,y=4k,z=5k,代入代数式中,约去k,即可得到答案.
【解答】解:(1)分式的分子、分母都除以b2,
故答案为:约分;
(2)∵=,
∴b=2a,
∴原式=
=
=;
(3)设=k(k≠0),
则x=3k,y=4k,z=5k,
∴原式=
=
=.
26.(10分)已知:如图1,△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到点A,使DA=DF,延长BF交AC于点E.
(1)求证:△BDF≌△CDA;
(2)试说明:△ABC是等腰三角形;
(3)连接AF并延长,交BC于点G,如图2,求证:AG⊥BC.
【分析】(1)由SAS证明△FBD≌△ACD即可;
(2)由全等三角形的性质得∠DBF=∠DCA,再证△ABE≌△CBE(ASA),得AB=CB,即可得出结论;
(3)由全等三角形的性质得AD=DF,DB=DC,则∠DAF=∠DFA=45°,再由等腰直角三角形的性质得∠DCB=45°,然后证∠FGC=90°,即可得出结论.
【解答】证明:(1)∵∠BDC=90°,
∴∠CDA=90°=∠BDF,BD=CD,
又∵DF=DA,
∴△FBD≌△ACD(SAS);
(2)由(1)得:△FBD≌△ACD,
∴∠DBF=∠DCA,
∵∠CDA=90°,
∴∠DAC+∠A=90°,
∴∠DBF+∠A=90°,
∴∠AEB=180°﹣(∠DBF+∠A)=90°,
∴∠CEB=90°=∠AEB,
∵BF平分∠DBC,
∴∠ABF=∠CBF,
又∵BE=BE,
∴△ABE≌△CBE(ASA),
∴AB=CB,
∴△ABC是等腰三角形;
(3)由(1)得:△FBD≌△ACD,
∴AD=DF,DB=DC,
∵∠ADF=90°,
∴∠DAF=∠DFA=45°,
∵△DBC是等腰直角三角形,∠BDC=90°,
∴∠DCB=45°,
∵∠GFC=∠DFA=45°,
∴∠FGC=180°﹣45°﹣45°=90°,
∴AG⊥BC.
同课章节目录
