《1.1 分式》提高训练-2021-2022学年湘教八上数学(Word版含答案)
文档属性
| 名称 | 《1.1 分式》提高训练-2021-2022学年湘教八上数学(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 11:26:14 | ||
图片预览


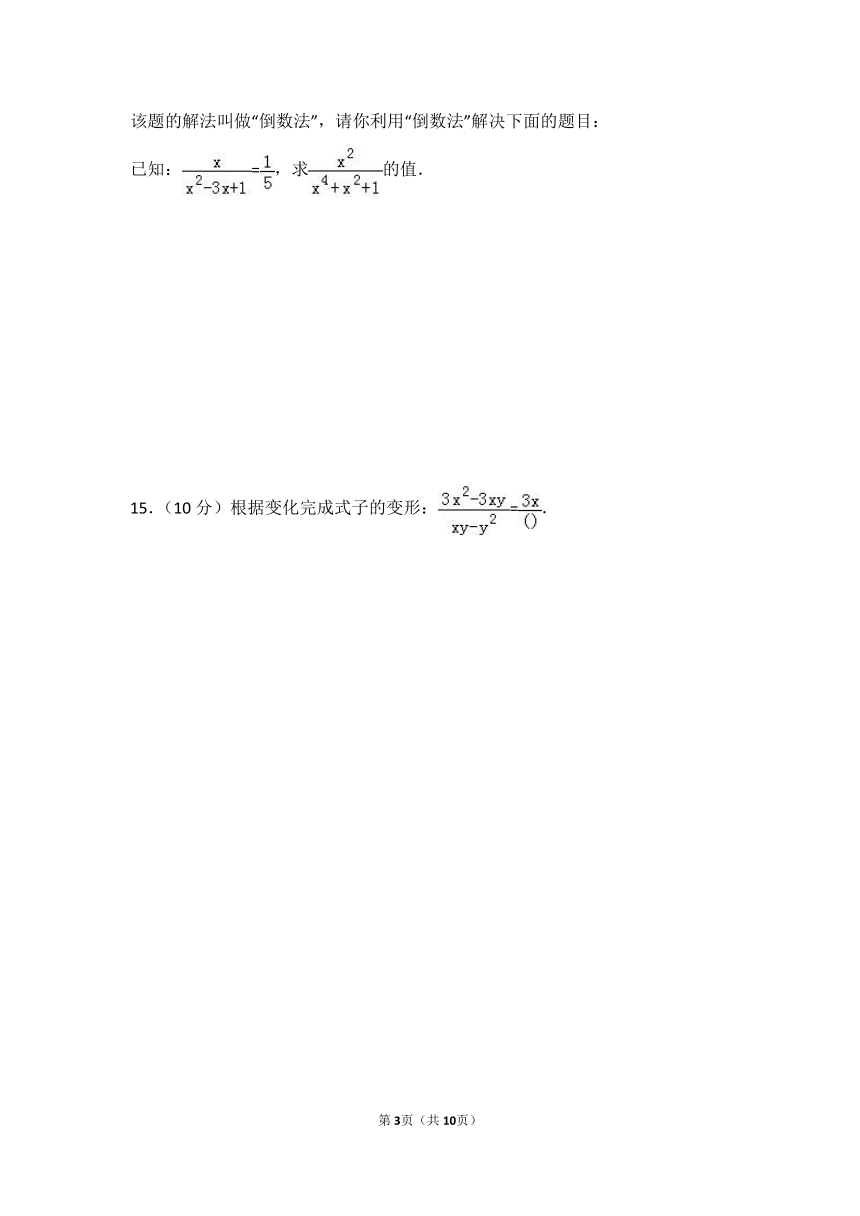


文档简介
《分式》提高训练
一、选择题(
本大题共5小题,共25分)
1.(5分)若分式的值等于0,则x的取值是( )
A.x=0
B.x=3
C.x=﹣3
D.x=3或x=﹣3
2.(5分)下列分式中,是最简分式的是( )
A.
B.
C.
D.
3.(5分)若分式的值为零,则x的值为( )
A.﹣2
B.2
C.±2
D.3
4.(5分)分式,,﹣的最简公分母为( )
A.2xy2
B.5xy
C.10xy2
D.10x2y2
5.(5分)甲、乙两城市之间的高铁全程长1500km,列车运行速度为bkm/h,经过长时间试运行后,铁路部门决定将列车运行速度再提高50km/h,则提速后列车跑完全程可省时( )
A.h
B.h
C.h
D.h
二、填空题(
本大题共5小题,共25分)
6.(5分)化简:=
.
7.(5分)若分式的值为0,则x的值为
.
8.(5分)已知=2,则=
.
9.(5分)在括号内填上适当地整式,使下列等式成立:=.
10.(5分)若a>0,b>0,且a2+b2=4ab,a≠b,则=
.
三、解答题(
本大题共5小题,共50分)
11.(10分)先约分,再求值:,其中x=﹣2,y=﹣.
12.(10分)若分式A,B的和化简后是整式,则称A,B是一对整合分式.
(1)判断与是否是一对整合分式,并说明理由;
(2)已知分式M,N是一对整合分式,,直接写出两个符合题意的分式N.
13.(10分)先约分,再求值:,其中a=2,b=
14.(10分)阅读下面的解题过程:
已知:=,求的值.
解:由
=知x≠0,所以,即x+=3.
所以=x2+=(x+)2﹣2=32﹣2=7.
故的值为.
该题的解法叫做“倒数法”,请你利用“倒数法”解决下面的题目:
已知:=,求的值.
15.(10分)根据变化完成式子的变形:=.
《分式》提高训练
参考答案与试题解析
一、选择题(
本大题共5小题,共25分)
1.(5分)若分式的值等于0,则x的取值是( )
A.x=0
B.x=3
C.x=﹣3
D.x=3或x=﹣3
【分析】直接利用分式的值为零则分子为零分母不为零,进而得出答案.
【解答】解:∵分式的值等于0,
∴|x|﹣3=0,2x﹣6≠0,
解得:x=﹣3,
故选:C.
【点评】此题主要考查了分式的值为零的条件,正确把握定义是解题关键.
2.(5分)下列分式中,是最简分式的是( )
A.
B.
C.
D.
【分析】根据最简分式的标准是分子,分母中不含有公因式,不能再约分,判断的方法是把分子、分母分解因式,然后对每一选项进行整理,即可得出答案.
【解答】解:A.=,不符合题意;
B.=,不符合题意;
C.=,不符合题意;
D.是最简分式,符合题意;
故选:D.
【点评】本题考查了最简分式,分式的化简过程,首先要把分子分母分解因式,然后进行约分.
3.(5分)若分式的值为零,则x的值为( )
A.﹣2
B.2
C.±2
D.3
【分析】让分子为0,分母不等于0列式求值即可.
【解答】解:根据题意得:x2﹣4=0且2x﹣5≠0;
解得x=±2;
故选:C.
【点评】此题主要考查了分式的值为零,若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
4.(5分)分式,,﹣的最简公分母为( )
A.2xy2
B.5xy
C.10xy2
D.10x2y2
【分析】按照求最简公分母的方法计算即可.
【解答】解:分式,,﹣的最简公分母为10xy2,
故选:C.
【点评】本题主要考查最简公分母,通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.一般方法:①如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数,相同字母的最高次幂,所有不同字母都写在积里.②如果各分母都是多项式,就可以将各个分母因式分解,取各分母数字系数的最小公倍数,凡出现的字母(或含字母的整式)为底数的幂的因式都要取最高次幂.
5.(5分)甲、乙两城市之间的高铁全程长1500km,列车运行速度为bkm/h,经过长时间试运行后,铁路部门决定将列车运行速度再提高50km/h,则提速后列车跑完全程可省时( )
A.h
B.h
C.h
D.h
【分析】先根据时间=路程÷速度表示出提速前和提速后的时间,再相减,计算可得.
【解答】解:根据题意,提速前跑完全程所需时间为h,提速后跑完全程所需时间是h,
则提速后列车跑完全程可省时﹣==h,
故选:B.
【点评】本题主要考查列代数式,解题的关键是掌握时间=路程÷速度的基本关系和分式的减法运算法则.
二、填空题(
本大题共5小题,共25分)
6.(5分)化简:= ﹣ .
【分析】先将分母因式分解,再约去分子、分母的公因式即可得.
【解答】解:==﹣,
故答案为:﹣.
【点评】本题主要考查约分,由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.
7.(5分)若分式的值为0,则x的值为 ﹣3 .
【分析】根据分式值为0的条件:分子为0,分母不为0,求出x的值即可.
【解答】解:根据题意得:x2+x﹣6=0,且|x|﹣2≠0,
方程分解因式得:(x﹣2)(x+3)=0,
可得x﹣2=0或x+3=0,
解得:x=2(舍去)或x=﹣3,
则x的值为﹣3.
故答案为:﹣3.
【点评】此题考查了解一元二次方程﹣因式分解法,以及分式值为零的条件,做题时注意分母不为0的条件.
8.(5分)已知=2,则= ﹣1 .
【分析】根据已知得:a=2b,代入所求分式,将所有的a换成2b,化简可得结论.
【解答】解:∵=2,
∴a=2b,
则,
=,
=,
=﹣1.
故答案为:﹣1.
【点评】此题主要考查了分式的值,正确得出a,b的关系是解题关键.
9.(5分)在括号内填上适当地整式,使下列等式成立:=. a2+ab
【分析】直接利用分式的基本性质分析得出答案.
【解答】解:=.
故答案为:a2+ab.
【点评】此题主要考查了分式的基本性质,正确通分是解题关键.
10.(5分)若a>0,b>0,且a2+b2=4ab,a≠b,则= .
【分析】根据题目中的式子可以求得a+b和a﹣b的值,从而可以解答本题.
【解答】解:∵a>0,b>0,且a2+b2=4ab,a≠b,
∴(a+b)2=6ab,(a﹣b)2=2ab,
∴a+b=,a﹣b=,
∴,
故答案为:.
【点评】本题考查分式的值,解答本题的关键是明确分式求值的方法.
三、解答题(
本大题共5小题,共50分)
11.(10分)先约分,再求值:,其中x=﹣2,y=﹣.
【分析】先把分子分母因式分解,再约分得到原式=,然后把x、y的值代入计算即可.
【解答】解:原式=
=,
当x=﹣2,y=﹣时,原式==.
【点评】本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.
12.(10分)若分式A,B的和化简后是整式,则称A,B是一对整合分式.
(1)判断与是否是一对整合分式,并说明理由;
(2)已知分式M,N是一对整合分式,,直接写出两个符合题意的分式N.
【分析】(1)根据整合分式的定义即可求出答案.
(2)根据整合分式的定义以及分式的运算法则即可求出答案.
【解答】解:(1)是一对整合分式,理由如下:
∵===x
满足一对整合分式的定义,
∴与是一对整合分式.(
(2)答案不唯一,如,.
【点评】本题考查分式的基本性质,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
13.(10分)先约分,再求值:,其中a=2,b=
【分析】原式约分得到最简结果,把a与b的值代入计算即可求出值.
【解答】解:原式=
=
把a=2,b=代入
原式==.
【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
14.(10分)阅读下面的解题过程:
已知:=,求的值.
解:由
=知x≠0,所以,即x+=3.
所以=x2+=(x+)2﹣2=32﹣2=7.
故的值为.
该题的解法叫做“倒数法”,请你利用“倒数法”解决下面的题目:
已知:=,求的值.
【分析】根据题意给出的解题思路即可求出答案.
【解答】解:∵,且x≠0,
∴,
∴x+﹣3=5,
∴x+=8,
∴=x2++1=(x+)2﹣1=63,
∴=
【点评】本题考查分式的运算,解题的关键正确理解题目给出的解答思路,本题属于基础题型.
15.(10分)根据变化完成式子的变形:=.
【分析】根据分式的基本性质,分式有意义,则可对分子、分母先提取公因式,再化简解答.
【解答】解:提取公因式,得,
=,
分式有意义,则y≠0且x﹣y≠0,
化简得,原式=;
故答案为:y
【点评】本题主要考查了分式基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.
第10页(共10页)
一、选择题(
本大题共5小题,共25分)
1.(5分)若分式的值等于0,则x的取值是( )
A.x=0
B.x=3
C.x=﹣3
D.x=3或x=﹣3
2.(5分)下列分式中,是最简分式的是( )
A.
B.
C.
D.
3.(5分)若分式的值为零,则x的值为( )
A.﹣2
B.2
C.±2
D.3
4.(5分)分式,,﹣的最简公分母为( )
A.2xy2
B.5xy
C.10xy2
D.10x2y2
5.(5分)甲、乙两城市之间的高铁全程长1500km,列车运行速度为bkm/h,经过长时间试运行后,铁路部门决定将列车运行速度再提高50km/h,则提速后列车跑完全程可省时( )
A.h
B.h
C.h
D.h
二、填空题(
本大题共5小题,共25分)
6.(5分)化简:=
.
7.(5分)若分式的值为0,则x的值为
.
8.(5分)已知=2,则=
.
9.(5分)在括号内填上适当地整式,使下列等式成立:=.
10.(5分)若a>0,b>0,且a2+b2=4ab,a≠b,则=
.
三、解答题(
本大题共5小题,共50分)
11.(10分)先约分,再求值:,其中x=﹣2,y=﹣.
12.(10分)若分式A,B的和化简后是整式,则称A,B是一对整合分式.
(1)判断与是否是一对整合分式,并说明理由;
(2)已知分式M,N是一对整合分式,,直接写出两个符合题意的分式N.
13.(10分)先约分,再求值:,其中a=2,b=
14.(10分)阅读下面的解题过程:
已知:=,求的值.
解:由
=知x≠0,所以,即x+=3.
所以=x2+=(x+)2﹣2=32﹣2=7.
故的值为.
该题的解法叫做“倒数法”,请你利用“倒数法”解决下面的题目:
已知:=,求的值.
15.(10分)根据变化完成式子的变形:=.
《分式》提高训练
参考答案与试题解析
一、选择题(
本大题共5小题,共25分)
1.(5分)若分式的值等于0,则x的取值是( )
A.x=0
B.x=3
C.x=﹣3
D.x=3或x=﹣3
【分析】直接利用分式的值为零则分子为零分母不为零,进而得出答案.
【解答】解:∵分式的值等于0,
∴|x|﹣3=0,2x﹣6≠0,
解得:x=﹣3,
故选:C.
【点评】此题主要考查了分式的值为零的条件,正确把握定义是解题关键.
2.(5分)下列分式中,是最简分式的是( )
A.
B.
C.
D.
【分析】根据最简分式的标准是分子,分母中不含有公因式,不能再约分,判断的方法是把分子、分母分解因式,然后对每一选项进行整理,即可得出答案.
【解答】解:A.=,不符合题意;
B.=,不符合题意;
C.=,不符合题意;
D.是最简分式,符合题意;
故选:D.
【点评】本题考查了最简分式,分式的化简过程,首先要把分子分母分解因式,然后进行约分.
3.(5分)若分式的值为零,则x的值为( )
A.﹣2
B.2
C.±2
D.3
【分析】让分子为0,分母不等于0列式求值即可.
【解答】解:根据题意得:x2﹣4=0且2x﹣5≠0;
解得x=±2;
故选:C.
【点评】此题主要考查了分式的值为零,若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
4.(5分)分式,,﹣的最简公分母为( )
A.2xy2
B.5xy
C.10xy2
D.10x2y2
【分析】按照求最简公分母的方法计算即可.
【解答】解:分式,,﹣的最简公分母为10xy2,
故选:C.
【点评】本题主要考查最简公分母,通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.一般方法:①如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数,相同字母的最高次幂,所有不同字母都写在积里.②如果各分母都是多项式,就可以将各个分母因式分解,取各分母数字系数的最小公倍数,凡出现的字母(或含字母的整式)为底数的幂的因式都要取最高次幂.
5.(5分)甲、乙两城市之间的高铁全程长1500km,列车运行速度为bkm/h,经过长时间试运行后,铁路部门决定将列车运行速度再提高50km/h,则提速后列车跑完全程可省时( )
A.h
B.h
C.h
D.h
【分析】先根据时间=路程÷速度表示出提速前和提速后的时间,再相减,计算可得.
【解答】解:根据题意,提速前跑完全程所需时间为h,提速后跑完全程所需时间是h,
则提速后列车跑完全程可省时﹣==h,
故选:B.
【点评】本题主要考查列代数式,解题的关键是掌握时间=路程÷速度的基本关系和分式的减法运算法则.
二、填空题(
本大题共5小题,共25分)
6.(5分)化简:= ﹣ .
【分析】先将分母因式分解,再约去分子、分母的公因式即可得.
【解答】解:==﹣,
故答案为:﹣.
【点评】本题主要考查约分,由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.
7.(5分)若分式的值为0,则x的值为 ﹣3 .
【分析】根据分式值为0的条件:分子为0,分母不为0,求出x的值即可.
【解答】解:根据题意得:x2+x﹣6=0,且|x|﹣2≠0,
方程分解因式得:(x﹣2)(x+3)=0,
可得x﹣2=0或x+3=0,
解得:x=2(舍去)或x=﹣3,
则x的值为﹣3.
故答案为:﹣3.
【点评】此题考查了解一元二次方程﹣因式分解法,以及分式值为零的条件,做题时注意分母不为0的条件.
8.(5分)已知=2,则= ﹣1 .
【分析】根据已知得:a=2b,代入所求分式,将所有的a换成2b,化简可得结论.
【解答】解:∵=2,
∴a=2b,
则,
=,
=,
=﹣1.
故答案为:﹣1.
【点评】此题主要考查了分式的值,正确得出a,b的关系是解题关键.
9.(5分)在括号内填上适当地整式,使下列等式成立:=. a2+ab
【分析】直接利用分式的基本性质分析得出答案.
【解答】解:=.
故答案为:a2+ab.
【点评】此题主要考查了分式的基本性质,正确通分是解题关键.
10.(5分)若a>0,b>0,且a2+b2=4ab,a≠b,则= .
【分析】根据题目中的式子可以求得a+b和a﹣b的值,从而可以解答本题.
【解答】解:∵a>0,b>0,且a2+b2=4ab,a≠b,
∴(a+b)2=6ab,(a﹣b)2=2ab,
∴a+b=,a﹣b=,
∴,
故答案为:.
【点评】本题考查分式的值,解答本题的关键是明确分式求值的方法.
三、解答题(
本大题共5小题,共50分)
11.(10分)先约分,再求值:,其中x=﹣2,y=﹣.
【分析】先把分子分母因式分解,再约分得到原式=,然后把x、y的值代入计算即可.
【解答】解:原式=
=,
当x=﹣2,y=﹣时,原式==.
【点评】本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.
12.(10分)若分式A,B的和化简后是整式,则称A,B是一对整合分式.
(1)判断与是否是一对整合分式,并说明理由;
(2)已知分式M,N是一对整合分式,,直接写出两个符合题意的分式N.
【分析】(1)根据整合分式的定义即可求出答案.
(2)根据整合分式的定义以及分式的运算法则即可求出答案.
【解答】解:(1)是一对整合分式,理由如下:
∵===x
满足一对整合分式的定义,
∴与是一对整合分式.(
(2)答案不唯一,如,.
【点评】本题考查分式的基本性质,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
13.(10分)先约分,再求值:,其中a=2,b=
【分析】原式约分得到最简结果,把a与b的值代入计算即可求出值.
【解答】解:原式=
=
把a=2,b=代入
原式==.
【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
14.(10分)阅读下面的解题过程:
已知:=,求的值.
解:由
=知x≠0,所以,即x+=3.
所以=x2+=(x+)2﹣2=32﹣2=7.
故的值为.
该题的解法叫做“倒数法”,请你利用“倒数法”解决下面的题目:
已知:=,求的值.
【分析】根据题意给出的解题思路即可求出答案.
【解答】解:∵,且x≠0,
∴,
∴x+﹣3=5,
∴x+=8,
∴=x2++1=(x+)2﹣1=63,
∴=
【点评】本题考查分式的运算,解题的关键正确理解题目给出的解答思路,本题属于基础题型.
15.(10分)根据变化完成式子的变形:=.
【分析】根据分式的基本性质,分式有意义,则可对分子、分母先提取公因式,再化简解答.
【解答】解:提取公因式,得,
=,
分式有意义,则y≠0且x﹣y≠0,
化简得,原式=;
故答案为:y
【点评】本题主要考查了分式基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.
第10页(共10页)
同课章节目录
