1.3.2《空间向量及其运算的坐标表示》(共24张PPT)
文档属性
| 名称 | 1.3.2《空间向量及其运算的坐标表示》(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 14:33:44 | ||
图片预览




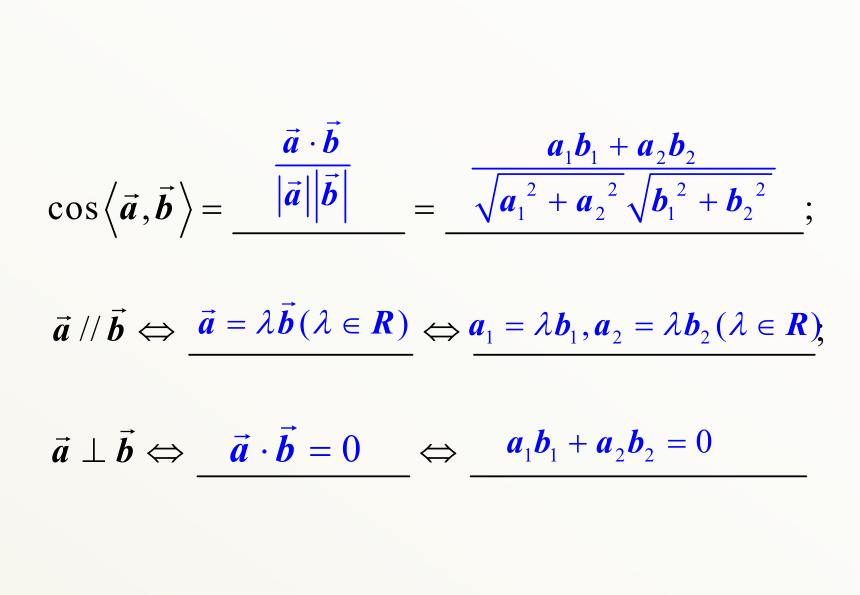




文档简介
(共24张PPT)
1.3.2
空间向量运算的坐标表示
第一章
空间向量与立体几何
本节课主要学习空间直角坐标系,空间向量运算的坐标表示.本课件以复习平面向量运算的坐标表示入手,提出了新问题:空间向量运算的坐标表示,引入新课。以学生自我探究为主,运用类比的思想学习空间向量运算的坐标表示,教会学生准确的建立坐标系,用空间向量坐标解决空间几何的线面关系.通过用空间向量解决简单的立体几何中的平行、垂直、夹角、距离(模)等问题,
培养学生的观察能力和探索能力,总结一般性方法.提高学生运用坐标法解决几何问题的能力,懂得欣赏数学的“简洁美”,并渗透数形结合和等价转化的数学思想方法.
通过平面向量运算的有关方法,引出空间向量的运算,进一步体会“二维”与“三维”的关系.如何建立坐标系,求解坐标才更简单.例1是空间向量的坐标求解;例2是求长度、点坐标;例3是证明两条直线的垂直;例4利用空间向量求长,求角。
重点:空间向量运算的坐标表示。
难点:空间向量坐标表示及其运用。
复习平面向量运算的坐标表示:
有了空间向量的坐标表示,你能得出空间向量是怎样的呢
?
类比是我们探究规律的重要方法
向量的直角坐标运算
如何证明?
1.距离公式
(1)向量的长度(模)公式
注意:此公式的几何意义是表示长方体的对角线的长度。
距离与夹角
在空间直角坐标系中,已知 、
,则
(2)空间两点间的距离公式
有向线段的终点坐标减去起点的坐标
2.两个向量夹角公式
注意:
(1)当
时, 同向;
(2)当
时, 反向;
(3)当
时, 。
思考:当
及
时,夹角在什么范围内?
例1.
解:
典例展示
例2 已知 、 ,求:
(1)线段 的中点坐标和长度;
解:设 是 的中点,则
∴点 的坐标是 .
(2)到 两点距离相等的点 的
坐标 满足的条件。
解:点
到 的距离相等,则
化简整理,得
即到 两点距离相等的点的坐标 满
足的条件是
x
y
z
O
A
A’
B
B’
O’
变式:在直三棱柱ABO-A’B’O’中,∠AOB=90。
|AO|=4,|BO|=2,|AA’|=4,D为A’B’的中点,如图建立直角坐标系,则
D
M
1.已知向量a=(2,-3,1),b=(2,0,3),c=(0,0,2),则:
(1)a·(b+c)=__________;
(2)(a+2b)·(a-2b)=__________.
[答案] 9 -38
2.设a=(1,5,-1),b=(-2,3,5),若(ka+b)∥(a-3b),则k=__________.
今天你学到了什么呢?
1.基本知识:
(1)向量的加减、数乘和数量积运算的坐标表示;
(2)两个向量的夹角公式和垂直、平行判定的坐标表示。
2.思想方法:
用向量坐标法计算或证明几何问题
(1)
建立直角坐标系,
(2)把点、向量坐标化,
(3)对向量计算或证明。
课后练习
课后习题
1.3.2
空间向量运算的坐标表示
第一章
空间向量与立体几何
本节课主要学习空间直角坐标系,空间向量运算的坐标表示.本课件以复习平面向量运算的坐标表示入手,提出了新问题:空间向量运算的坐标表示,引入新课。以学生自我探究为主,运用类比的思想学习空间向量运算的坐标表示,教会学生准确的建立坐标系,用空间向量坐标解决空间几何的线面关系.通过用空间向量解决简单的立体几何中的平行、垂直、夹角、距离(模)等问题,
培养学生的观察能力和探索能力,总结一般性方法.提高学生运用坐标法解决几何问题的能力,懂得欣赏数学的“简洁美”,并渗透数形结合和等价转化的数学思想方法.
通过平面向量运算的有关方法,引出空间向量的运算,进一步体会“二维”与“三维”的关系.如何建立坐标系,求解坐标才更简单.例1是空间向量的坐标求解;例2是求长度、点坐标;例3是证明两条直线的垂直;例4利用空间向量求长,求角。
重点:空间向量运算的坐标表示。
难点:空间向量坐标表示及其运用。
复习平面向量运算的坐标表示:
有了空间向量的坐标表示,你能得出空间向量是怎样的呢
?
类比是我们探究规律的重要方法
向量的直角坐标运算
如何证明?
1.距离公式
(1)向量的长度(模)公式
注意:此公式的几何意义是表示长方体的对角线的长度。
距离与夹角
在空间直角坐标系中,已知 、
,则
(2)空间两点间的距离公式
有向线段的终点坐标减去起点的坐标
2.两个向量夹角公式
注意:
(1)当
时, 同向;
(2)当
时, 反向;
(3)当
时, 。
思考:当
及
时,夹角在什么范围内?
例1.
解:
典例展示
例2 已知 、 ,求:
(1)线段 的中点坐标和长度;
解:设 是 的中点,则
∴点 的坐标是 .
(2)到 两点距离相等的点 的
坐标 满足的条件。
解:点
到 的距离相等,则
化简整理,得
即到 两点距离相等的点的坐标 满
足的条件是
x
y
z
O
A
A’
B
B’
O’
变式:在直三棱柱ABO-A’B’O’中,∠AOB=90。
|AO|=4,|BO|=2,|AA’|=4,D为A’B’的中点,如图建立直角坐标系,则
D
M
1.已知向量a=(2,-3,1),b=(2,0,3),c=(0,0,2),则:
(1)a·(b+c)=__________;
(2)(a+2b)·(a-2b)=__________.
[答案] 9 -38
2.设a=(1,5,-1),b=(-2,3,5),若(ka+b)∥(a-3b),则k=__________.
今天你学到了什么呢?
1.基本知识:
(1)向量的加减、数乘和数量积运算的坐标表示;
(2)两个向量的夹角公式和垂直、平行判定的坐标表示。
2.思想方法:
用向量坐标法计算或证明几何问题
(1)
建立直角坐标系,
(2)把点、向量坐标化,
(3)对向量计算或证明。
课后练习
课后习题
