江西省重点中学联盟2021-2022学年高二上学期第一次月考数学试题(Word版含答案)
文档属性
| 名称 | 江西省重点中学联盟2021-2022学年高二上学期第一次月考数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 11:00:59 | ||
图片预览


文档简介
江西省重点中学联盟2021-2022学年高二上学期第一次月考
数学试卷
一、选择题(本题共12道小题,每小题5分,共60分)
1.若点(,2)在直线l:ax+y+1=0上,则直线l的倾斜角为( )
A.30°
B.45°
C.60°
D.120°
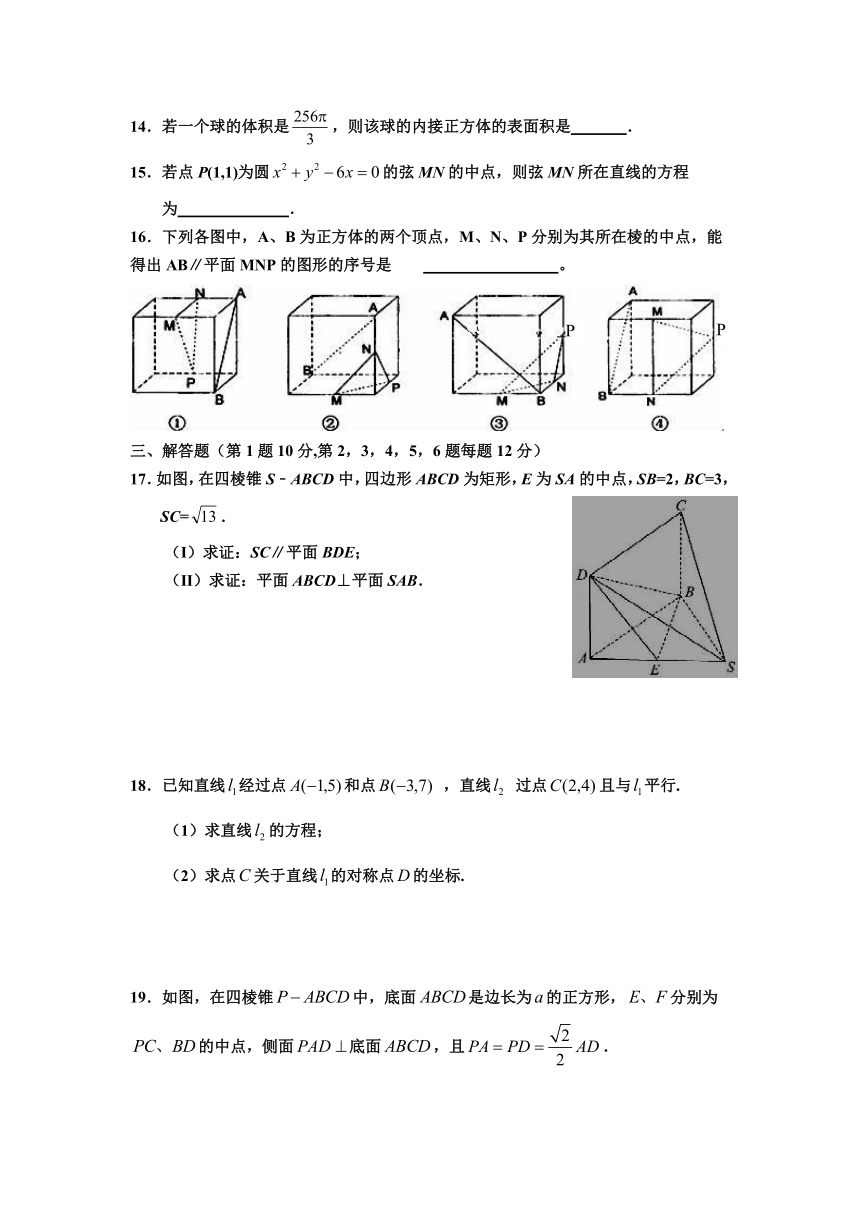
2.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(
).
A.32π
B.
28π
C.
24π
D.20π
(第2题图
)
(第3题图)
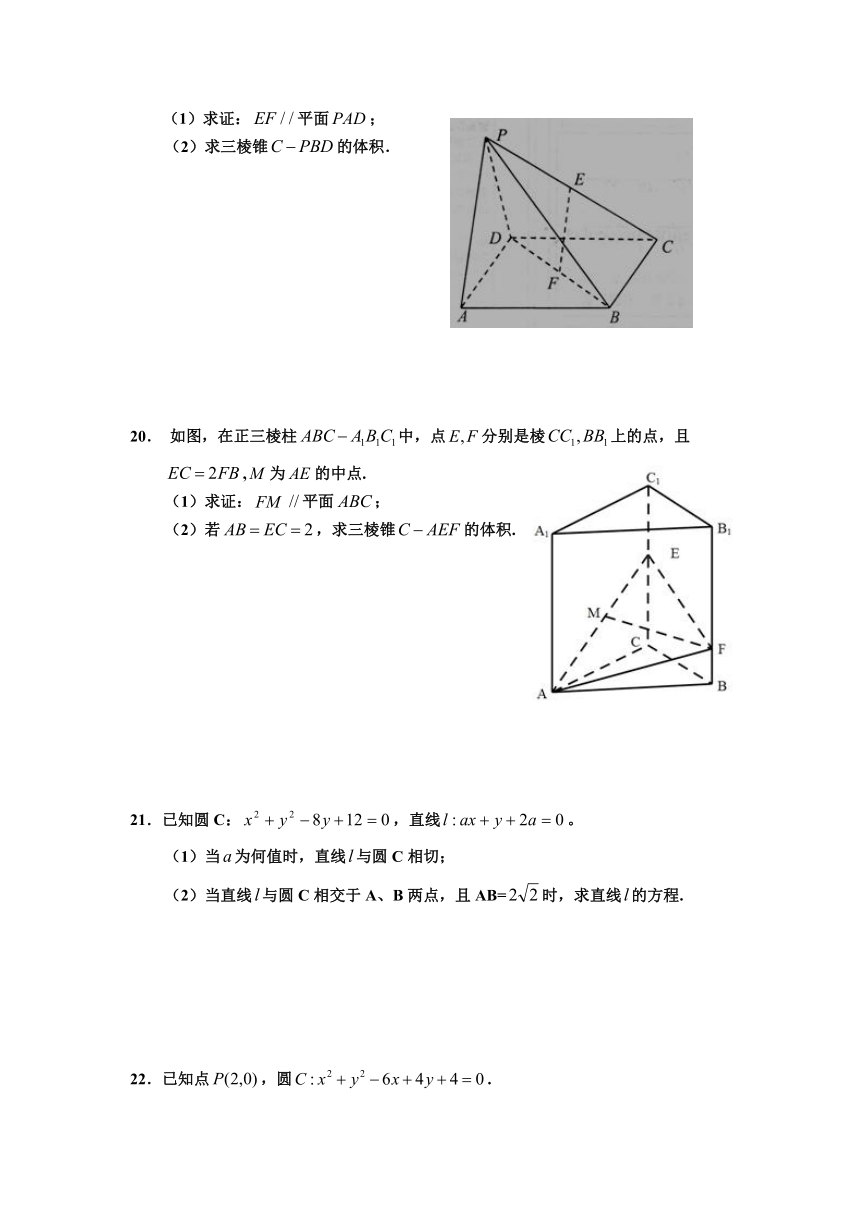
3.某三棱锥的三视图如图所示,则该三棱锥的表面积是(
)
A.5
B.
C.
D.
4.设有直线m、n和平面、,下列四个命题中,正确的是(
)
A.
若,m,则m
//
B.若m,n,m
//,n
//,则//
C.若,m,则m
D.
若m
//,,,则m
//
n
5.某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是(
)
A.3
B.
C.
D.2
6.直线通过点(1,3)且与两坐标轴的正半轴所围成的三
角形面积为6,则直线的方程是(
).
A.
B.
C.
D.
7.如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该几何体的体积为(
)
A.
B.2
C.
D.4
8.圆x2+y2+2x+6y+9=0与圆x2+y2﹣6x+2y+1=0的位置关系是( )
A.相交
B.相离
C.外切
D.内切
9.
一束光线从点出发,经轴反射到圆上的最短路径是(
)
A.
B.
C.
4
D.5
10.如图,正方体的棱线长为1,线段上有两个动点E,F,且,则下列结论中错误的是
(
)
A.
B.
C.
三棱锥的体积为定值
D.
11.若圆上至少有三个不同的点到直线:的距离为,则取值范围是(
)
A.(-2,2)
B.[-2,2]
C.[0,2]
D.[-2,2)
12.当曲线与直线有两个相异的交点时,实数的取值范围是
(
)
A.
B.
C.
D.
二、填空题(本题共4道小题,每小题5分,共20分)
13.已知直线与直线互相垂直,则实数m的值为
.
14.若一个球的体积是,则该球的内接正方体的表面积是
.
15.若点P(1,1)为圆的弦MN的中点,则弦MN所在直线的方程为
.
16.下列各图中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是
。
三、解答题(第1题10分,第2,3,4,5,6题每题12分)
17.如图,在四棱锥S﹣ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,SC=.
(Ⅰ)求证:SC∥平面BDE;
(Ⅱ)求证:平面ABCD⊥平面SAB.
18.已知直线经过点和点
,直线
过点且与平行.
(1)求直线的方程;
(2)求点关于直线的对称点的坐标.
19.如图,在四棱锥中,底面是边长为的正方形,分别为的中点,侧面底面,且.
(1)求证:平面;
(2)求三棱锥的体积.
20.
如图,在正三棱柱中,点分别是棱上的点,且,为的中点.
(1)求证:平面;
(2)若,求三棱锥的体积.
21.已知圆C:,直线。
(1)当为何值时,直线与圆C相切;
(2)当直线与圆C相交于A、B两点,且AB=时,求直线的方程.
22.已知点,圆.
(1)若直线过点且到圆心的距离为1,求直线的方程;
(2)设过点的直线与圆交于两点(的斜率为正),当
时,求以线段为直径的圆的方程.
数学试卷答案
一、选择题答案:CBDDA
AABCD
BC
二、填空题答案:13.
2
14.
128
15.
16.①③
17.证明:(Ⅰ)连接AC交BD于F,则F为AC中点,连接EF,
∵E为SA的中点,F为AC中点,∴EF∥SC,
又EF?面BDE,SC?面BDE,∴SC∥平面BDE.
(Ⅱ)∵SB=2,BC=3,,
∴SB2+BC2=SC2,∴BC⊥SB,
又四边形ABCD为矩形,
∴BC⊥AB,又AB、SB在平面SAB内且相交,
∴BC⊥平面SAB,
又BC?平面ABCD,
∴平面ABCD⊥平面SAB.
18.(1)由题意知,且过
代入点斜式有,即
.
(2)由(1)有且过,
代入点斜式有,即
设点,则
点的坐标为.
19.(1)连结,则是的中点,为的中点,
故在中,,
且平面,平面,∴平面;
(2)取的中点,连结,∵,∴,
又平面平面,平面平面,
∴平面,
∴.
20.(1)略(2)
21.(1)把圆C:,化为,得圆心,半径,再求圆心到直线的距离,,解得.
(2)设圆心到直线的距离,则,则,得或;直线的方程为:或
22.(Ⅰ)由题意知,圆的标准方程为:
,
∴圆心,半径,
①当直线的斜率存在时,设直线的方程为,即,
∴,解得,
∴直线的方程为,即.
②当直线的斜率不存在时,直线的方程为,
此时直线到圆心的距离为1,符合题意.
综上,直线的方程为或.
(Ⅱ)设过点的直线的方程为即,
则圆心到直线的距离,
解得,∴直线的方程为即,
联立直线与圆的方程得,
消去得,则中点的纵坐标为,
把代入直线中得,∴
中点的坐标为,
由题意知,所求圆的半径为:
,
∴以线段为直径的圆的方程为:
.
P
P
数学试卷
一、选择题(本题共12道小题,每小题5分,共60分)
1.若点(,2)在直线l:ax+y+1=0上,则直线l的倾斜角为( )
A.30°
B.45°
C.60°
D.120°
2.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(
).
A.32π
B.
28π
C.
24π
D.20π
(第2题图
)
(第3题图)
3.某三棱锥的三视图如图所示,则该三棱锥的表面积是(
)
A.5
B.
C.
D.
4.设有直线m、n和平面、,下列四个命题中,正确的是(
)
A.
若,m,则m
//
B.若m,n,m
//,n
//,则//
C.若,m,则m
D.
若m
//,,,则m
//
n
5.某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是(
)
A.3
B.
C.
D.2
6.直线通过点(1,3)且与两坐标轴的正半轴所围成的三
角形面积为6,则直线的方程是(
).
A.
B.
C.
D.
7.如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该几何体的体积为(
)
A.
B.2
C.
D.4
8.圆x2+y2+2x+6y+9=0与圆x2+y2﹣6x+2y+1=0的位置关系是( )
A.相交
B.相离
C.外切
D.内切
9.
一束光线从点出发,经轴反射到圆上的最短路径是(
)
A.
B.
C.
4
D.5
10.如图,正方体的棱线长为1,线段上有两个动点E,F,且,则下列结论中错误的是
(
)
A.
B.
C.
三棱锥的体积为定值
D.
11.若圆上至少有三个不同的点到直线:的距离为,则取值范围是(
)
A.(-2,2)
B.[-2,2]
C.[0,2]
D.[-2,2)
12.当曲线与直线有两个相异的交点时,实数的取值范围是
(
)
A.
B.
C.
D.
二、填空题(本题共4道小题,每小题5分,共20分)
13.已知直线与直线互相垂直,则实数m的值为
.
14.若一个球的体积是,则该球的内接正方体的表面积是
.
15.若点P(1,1)为圆的弦MN的中点,则弦MN所在直线的方程为
.
16.下列各图中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是
。
三、解答题(第1题10分,第2,3,4,5,6题每题12分)
17.如图,在四棱锥S﹣ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,SC=.
(Ⅰ)求证:SC∥平面BDE;
(Ⅱ)求证:平面ABCD⊥平面SAB.
18.已知直线经过点和点
,直线
过点且与平行.
(1)求直线的方程;
(2)求点关于直线的对称点的坐标.
19.如图,在四棱锥中,底面是边长为的正方形,分别为的中点,侧面底面,且.
(1)求证:平面;
(2)求三棱锥的体积.
20.
如图,在正三棱柱中,点分别是棱上的点,且,为的中点.
(1)求证:平面;
(2)若,求三棱锥的体积.
21.已知圆C:,直线。
(1)当为何值时,直线与圆C相切;
(2)当直线与圆C相交于A、B两点,且AB=时,求直线的方程.
22.已知点,圆.
(1)若直线过点且到圆心的距离为1,求直线的方程;
(2)设过点的直线与圆交于两点(的斜率为正),当
时,求以线段为直径的圆的方程.
数学试卷答案
一、选择题答案:CBDDA
AABCD
BC
二、填空题答案:13.
2
14.
128
15.
16.①③
17.证明:(Ⅰ)连接AC交BD于F,则F为AC中点,连接EF,
∵E为SA的中点,F为AC中点,∴EF∥SC,
又EF?面BDE,SC?面BDE,∴SC∥平面BDE.
(Ⅱ)∵SB=2,BC=3,,
∴SB2+BC2=SC2,∴BC⊥SB,
又四边形ABCD为矩形,
∴BC⊥AB,又AB、SB在平面SAB内且相交,
∴BC⊥平面SAB,
又BC?平面ABCD,
∴平面ABCD⊥平面SAB.
18.(1)由题意知,且过
代入点斜式有,即
.
(2)由(1)有且过,
代入点斜式有,即
设点,则
点的坐标为.
19.(1)连结,则是的中点,为的中点,
故在中,,
且平面,平面,∴平面;
(2)取的中点,连结,∵,∴,
又平面平面,平面平面,
∴平面,
∴.
20.(1)略(2)
21.(1)把圆C:,化为,得圆心,半径,再求圆心到直线的距离,,解得.
(2)设圆心到直线的距离,则,则,得或;直线的方程为:或
22.(Ⅰ)由题意知,圆的标准方程为:
,
∴圆心,半径,
①当直线的斜率存在时,设直线的方程为,即,
∴,解得,
∴直线的方程为,即.
②当直线的斜率不存在时,直线的方程为,
此时直线到圆心的距离为1,符合题意.
综上,直线的方程为或.
(Ⅱ)设过点的直线的方程为即,
则圆心到直线的距离,
解得,∴直线的方程为即,
联立直线与圆的方程得,
消去得,则中点的纵坐标为,
把代入直线中得,∴
中点的坐标为,
由题意知,所求圆的半径为:
,
∴以线段为直径的圆的方程为:
.
P
P
同课章节目录
