鲁教版(五四制)九年级上学期 2.5三角函数的应用 同步训练(word版、含答案解析)
文档属性
| 名称 | 鲁教版(五四制)九年级上学期 2.5三角函数的应用 同步训练(word版、含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 426.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览


文档简介
2.5三角函数的应用
一、选择题
有一坡角为的滑雪道,滑雪道长为100米,坡顶到坡底的竖直高度为
A.
B.
C.
D.
如图,某地修建高速公路,要从A地向B地修一条隧道点A,B在同一水平面上为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则A,B两地之间的距离为
A.
米
B.
米
C.
米
D.
米
如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:在点C处放置测角仪,测得旗杆顶的仰角;
量得测角仪的高度;
量得测角仪到旗杆的水平距离.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A.
B.
C.
D.
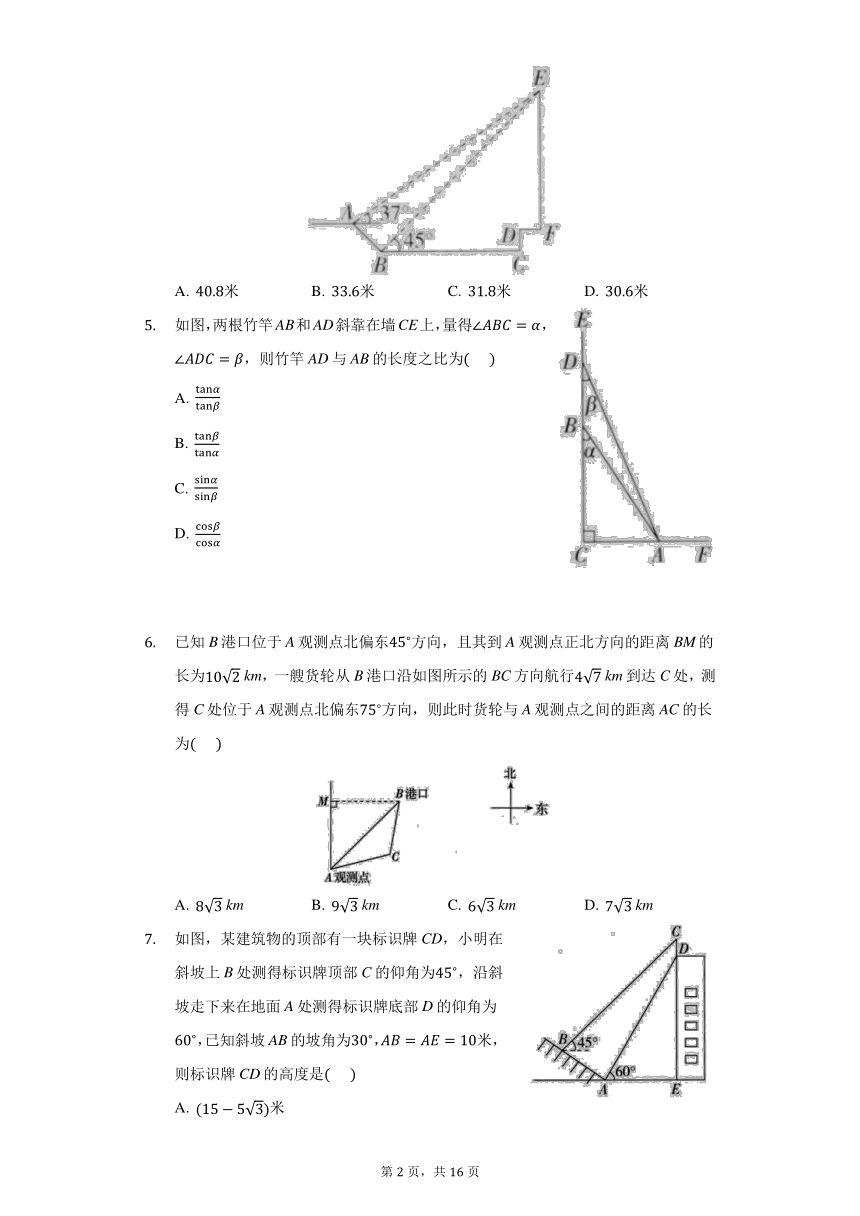
一天,小明和朋友一起到小区测量小明所住楼房的高度,如图,他们首先在A处测得楼房顶部E的仰角为,然后沿着斜坡AB走了米到B处,再测得楼房顶部E的仰角为,身高忽略不计已知斜坡AB的坡度,楼房EF底部距BC的高度CD为米,点A,B,C,D,E,F在同一平面内,则楼房自身高度EF大约为参考数据:,,?
?
A.
米
B.
米
C.
米
D.
米
如图,两根竹竿AB和AD斜靠在墙CE上,量得,,则竹竿AD与AB的长度之比为?
?
A.
B.
C.
D.
已知B港口位于A观测点北偏东方向,且其到A观测点正北方向的距离BM的长为?km,一艘货轮从B港口沿如图所示的BC方向航行?km到达C处,测得C处位于A观测点北偏东方向,则此时货轮与A观测点之间的距离AC的长为?
?
A.
?km
B.
?km
C.
?km
D.
?km
如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为,沿斜坡走下来在地面A处测得标识牌底部D的仰角为,已知斜坡AB的坡角为,米,则标识牌CD的高度是?
?
A.
米
B.
米
C.
米
D.
米
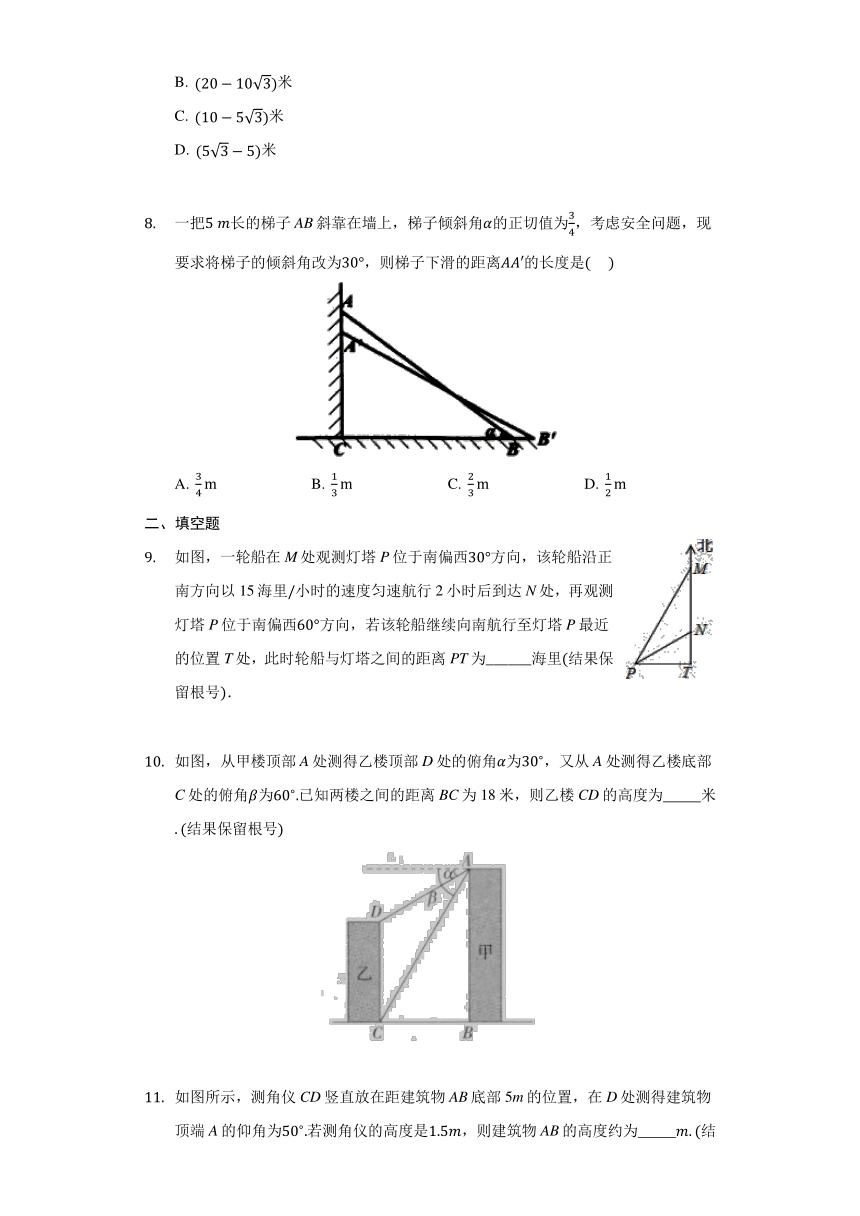
一把长的梯子AB斜靠在墙上,梯子倾斜角的正切值为,考虑安全问题,现要求将梯子的倾斜角改为,则梯子下滑的距离的长度是???
A.
B.
C.
D.
二、填空题
如图,一轮船在M处观测灯塔P位于南偏西方向,该轮船沿正南方向以15海里小时的速度匀速航行2小时后到达N处,再观测灯塔P位于南偏西方向,若该轮船继续向南航行至灯塔P最近的位置T处,此时轮船与灯塔之间的距离PT为______海里结果保留根号.
如图,从甲楼顶部A处测得乙楼顶部D处的俯角为,又从A处测得乙楼底部C处的俯角为已知两楼之间的距离BC为18米,则乙楼CD的高度为??????????米结果保留根号
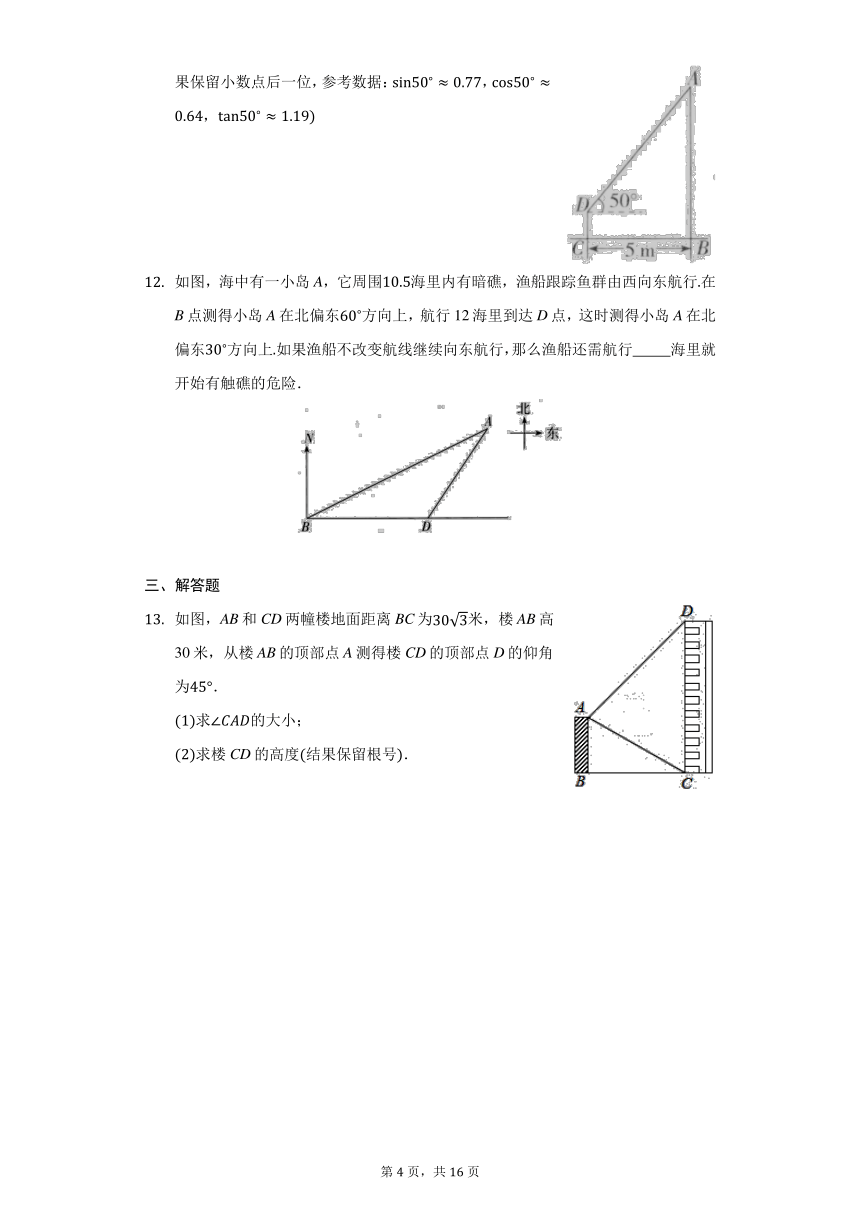
如图所示,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为若测角仪的高度是,则建筑物AB的高度约为??????????结果保留小数点后一位,参考数据:,,
如图,海中有一小岛A,它周围海里内有暗礁,渔船跟踪鱼群由西向东航行在B点测得小岛A在北偏东方向上,航行12海里到达D点,这时测得小岛A在北偏东方向上如果渔船不改变航线继续向东航行,那么渔船还需航行??????????海里就开始有触礁的危险.
三、解答题
如图,AB和CD两幢楼地面距离BC为米,楼AB高30米,从楼AB的顶部点A测得楼CD的顶部点D的仰角为.
求的大小;
求楼CD的高度结果保留根号.
某兴趣小组为了测量大楼CD的高度,先沿着斜坡AB走了52米到达坡顶点B处,然后在点B处测得大楼顶点C的仰角为,已知斜坡AB的坡度为:,点A到大楼的距离AD为72米,求大楼的高度CD.
参考数据:,,
某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为和,求桥AB的长度.
古代为了保护家园,在城池的四周修护城河,为了方便交通,在护城河上安装了吊桥如图所示,图是图的平面图,其中BD为城墙,AB为桥,AD为吊绳,当收紧吊绳时,桥AB运动到CB处,若,,,,求此时CD的长度.结果保留小数点后一位
答案和解析
1.【答案】D
【解析】解:,
,
故选:D.
根据正弦的定义进行解答即可.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
2.【答案】D
【解析】
【分析】本题考查解直角三角形的应用仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.
在中,,,米,根据,即可解决问题.
【解答】
解:在中,因为?,?,米,
所以?所以?米.
故选D.
??
3.【答案】A
【解析】
【分析】
本题主要考查解直角三角形的应用仰角俯角问题,掌握仰角俯角的定义,并根据题意构建合适的直角三角形是解题的关键.
过C作于F,则四边形BFCD是矩形,根据三角函数的定义即可得到结论.
【解答】
解:过C作于F,则四边形BFCD是矩形,
,,
,
,
,
,
故选A.??
4.【答案】C
【解析】解:如图,过A作交CB的延长线于点H,延长BC交EF的延长线于点G,作于点J,
则四边形AHGJ与四边形DCGF都是矩形,米,.
在中,米,,由勾股定理易得米,米,
,,,设米,则米,米,
在中,,,解得,即米,
米,
故选C.
5.【答案】C
【解析】解:在中,,即,,
在中,,即,
,,
故选C.
6.【答案】A
【解析】解:?,,?km,
?km,,
如图,过点B作,交AC的延长线于D,
在中,,,
,,,,?km,
在中,,?km,?km,
,
货轮与A观测点之间的距离AC的长为?km.
故选A.
7.【答案】A
【解析】解:过点B作,交直线AE于点M,过点B作于点N,如图所示,
则,,
在中,米,米.
在中,米,
在中,米,,
米,
米.
故选A.
8.【答案】D
【解析】
【分析】
本题考查了解直角三角形在实际生活中的应用,勾股定理,设,,根据勾股定理得到,求得,,根据直角三角形的性质得到结论.
【解答】
解:如图,
梯子倾斜角的正切值为,
设,,
,
,
,,
,,
,
,
故梯子下滑的距离的长度是,
故选D.??
9.【答案】
【解析】解:由题意得,海里,
,,
,
海里,
海里.
故答案为:.
根据“若该轮船继续向南航行至灯塔P最近的位置T处,此时轮船与灯塔之间的距离为PT”,得,利用锐角三角函数关系进行求解即可
本题考查解直角三角形的应用方向角问题,锐角三角函数等知识,解题的关键是求得PN的长度,属于中考常考题.
10.【答案】
【解析】?如图,过点A作交CD的延长线于E,则?米,
在中,
,
,
米
在中,
,
,
米,
米,
即乙楼CD的高度为米
11.【答案】
【解析】解:如图,过点D作,垂足为点E,
则,,
在中,
,
,
,
即建筑物AB的高度约为.
12.【答案】
【解析】解:如图,过A作,交直线BD于点C,则AC的长是A到BD的距离,
,,,?,
,
海里,?,,海里,
由勾股定理,得海里,
设渔船还需航行x海里就开始有触礁的危险,即到达点时有触礁的危险,
在中,由勾股定理,得,解得或舍,
渔船还需航行海里就开始有触礁的危险.
13.【答案】解:过A作于点E,
则米,米,
在中,,
则,
则;
在中,米,
米.
【解析】过A作于点E,可得米,米,在直角三角形中,利用锐角三角函数的定义求出,进一步求得的大小;
利用等腰直角三角形的性质求出DE的长,由求出CD的长即可.
此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解本题的关键.
14.【答案】解:如图,过点B作于点E,于点F,
,
易得四边形BEDF是矩形,
,,
在中,BE:::12,
设,,
根据勾股定理,得,
,
解得,
,
,
,
在中,,
米.
答:大楼的高度CD约为52米.
【解析】本题考查了解直角三角形的应用仰角俯角问题和坡度坡角问题,解决本题的关键是掌握仰角俯角和坡度坡角定义.
过点B作于点E,于点F,可得四边形BEDF是矩形,根据斜坡AB的坡度为:,设,,利用勾股定理可得x的值,再根据锐角三角函数即可进一步求大楼的高度CD.
15.【答案】解:如图示:过点C作,垂足为D,
由题意得,,,,
在中,米,
在中,,
米,
米.
答:桥AB的长度为米.
【解析】过点C作,垂足为D,根据在C处测得桥两端A,B两点的俯角分别为和,可得,,利用特殊角的三角函数求解即可.
本题考查了解直角三角形的应用,熟悉特殊角的三角函数值是解题的关键.
16.【答案】解:作于E,如图所示:
,
,,
由题意得:,
设,则,,
,
,
解得:,即,
又,
,
答:此时CD的长度约为.
【解析】本题考查了解直角三角形的应用;熟练掌握锐角三角函数的定义是解题的关键.
作于E,由直角三角形的性质得出,,由题意得:,设,则,,解直角三角形求出,即,再由锐角三角函数求出CD的长即可.
第4页,共16页
一、选择题
有一坡角为的滑雪道,滑雪道长为100米,坡顶到坡底的竖直高度为
A.
B.
C.
D.
如图,某地修建高速公路,要从A地向B地修一条隧道点A,B在同一水平面上为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则A,B两地之间的距离为
A.
米
B.
米
C.
米
D.
米
如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:在点C处放置测角仪,测得旗杆顶的仰角;
量得测角仪的高度;
量得测角仪到旗杆的水平距离.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A.
B.
C.
D.
一天,小明和朋友一起到小区测量小明所住楼房的高度,如图,他们首先在A处测得楼房顶部E的仰角为,然后沿着斜坡AB走了米到B处,再测得楼房顶部E的仰角为,身高忽略不计已知斜坡AB的坡度,楼房EF底部距BC的高度CD为米,点A,B,C,D,E,F在同一平面内,则楼房自身高度EF大约为参考数据:,,?
?
A.
米
B.
米
C.
米
D.
米
如图,两根竹竿AB和AD斜靠在墙CE上,量得,,则竹竿AD与AB的长度之比为?
?
A.
B.
C.
D.
已知B港口位于A观测点北偏东方向,且其到A观测点正北方向的距离BM的长为?km,一艘货轮从B港口沿如图所示的BC方向航行?km到达C处,测得C处位于A观测点北偏东方向,则此时货轮与A观测点之间的距离AC的长为?
?
A.
?km
B.
?km
C.
?km
D.
?km
如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为,沿斜坡走下来在地面A处测得标识牌底部D的仰角为,已知斜坡AB的坡角为,米,则标识牌CD的高度是?
?
A.
米
B.
米
C.
米
D.
米
一把长的梯子AB斜靠在墙上,梯子倾斜角的正切值为,考虑安全问题,现要求将梯子的倾斜角改为,则梯子下滑的距离的长度是???
A.
B.
C.
D.
二、填空题
如图,一轮船在M处观测灯塔P位于南偏西方向,该轮船沿正南方向以15海里小时的速度匀速航行2小时后到达N处,再观测灯塔P位于南偏西方向,若该轮船继续向南航行至灯塔P最近的位置T处,此时轮船与灯塔之间的距离PT为______海里结果保留根号.
如图,从甲楼顶部A处测得乙楼顶部D处的俯角为,又从A处测得乙楼底部C处的俯角为已知两楼之间的距离BC为18米,则乙楼CD的高度为??????????米结果保留根号
如图所示,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为若测角仪的高度是,则建筑物AB的高度约为??????????结果保留小数点后一位,参考数据:,,
如图,海中有一小岛A,它周围海里内有暗礁,渔船跟踪鱼群由西向东航行在B点测得小岛A在北偏东方向上,航行12海里到达D点,这时测得小岛A在北偏东方向上如果渔船不改变航线继续向东航行,那么渔船还需航行??????????海里就开始有触礁的危险.
三、解答题
如图,AB和CD两幢楼地面距离BC为米,楼AB高30米,从楼AB的顶部点A测得楼CD的顶部点D的仰角为.
求的大小;
求楼CD的高度结果保留根号.
某兴趣小组为了测量大楼CD的高度,先沿着斜坡AB走了52米到达坡顶点B处,然后在点B处测得大楼顶点C的仰角为,已知斜坡AB的坡度为:,点A到大楼的距离AD为72米,求大楼的高度CD.
参考数据:,,
某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为和,求桥AB的长度.
古代为了保护家园,在城池的四周修护城河,为了方便交通,在护城河上安装了吊桥如图所示,图是图的平面图,其中BD为城墙,AB为桥,AD为吊绳,当收紧吊绳时,桥AB运动到CB处,若,,,,求此时CD的长度.结果保留小数点后一位
答案和解析
1.【答案】D
【解析】解:,
,
故选:D.
根据正弦的定义进行解答即可.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
2.【答案】D
【解析】
【分析】本题考查解直角三角形的应用仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.
在中,,,米,根据,即可解决问题.
【解答】
解:在中,因为?,?,米,
所以?所以?米.
故选D.
??
3.【答案】A
【解析】
【分析】
本题主要考查解直角三角形的应用仰角俯角问题,掌握仰角俯角的定义,并根据题意构建合适的直角三角形是解题的关键.
过C作于F,则四边形BFCD是矩形,根据三角函数的定义即可得到结论.
【解答】
解:过C作于F,则四边形BFCD是矩形,
,,
,
,
,
,
故选A.??
4.【答案】C
【解析】解:如图,过A作交CB的延长线于点H,延长BC交EF的延长线于点G,作于点J,
则四边形AHGJ与四边形DCGF都是矩形,米,.
在中,米,,由勾股定理易得米,米,
,,,设米,则米,米,
在中,,,解得,即米,
米,
故选C.
5.【答案】C
【解析】解:在中,,即,,
在中,,即,
,,
故选C.
6.【答案】A
【解析】解:?,,?km,
?km,,
如图,过点B作,交AC的延长线于D,
在中,,,
,,,,?km,
在中,,?km,?km,
,
货轮与A观测点之间的距离AC的长为?km.
故选A.
7.【答案】A
【解析】解:过点B作,交直线AE于点M,过点B作于点N,如图所示,
则,,
在中,米,米.
在中,米,
在中,米,,
米,
米.
故选A.
8.【答案】D
【解析】
【分析】
本题考查了解直角三角形在实际生活中的应用,勾股定理,设,,根据勾股定理得到,求得,,根据直角三角形的性质得到结论.
【解答】
解:如图,
梯子倾斜角的正切值为,
设,,
,
,
,,
,,
,
,
故梯子下滑的距离的长度是,
故选D.??
9.【答案】
【解析】解:由题意得,海里,
,,
,
海里,
海里.
故答案为:.
根据“若该轮船继续向南航行至灯塔P最近的位置T处,此时轮船与灯塔之间的距离为PT”,得,利用锐角三角函数关系进行求解即可
本题考查解直角三角形的应用方向角问题,锐角三角函数等知识,解题的关键是求得PN的长度,属于中考常考题.
10.【答案】
【解析】?如图,过点A作交CD的延长线于E,则?米,
在中,
,
,
米
在中,
,
,
米,
米,
即乙楼CD的高度为米
11.【答案】
【解析】解:如图,过点D作,垂足为点E,
则,,
在中,
,
,
,
即建筑物AB的高度约为.
12.【答案】
【解析】解:如图,过A作,交直线BD于点C,则AC的长是A到BD的距离,
,,,?,
,
海里,?,,海里,
由勾股定理,得海里,
设渔船还需航行x海里就开始有触礁的危险,即到达点时有触礁的危险,
在中,由勾股定理,得,解得或舍,
渔船还需航行海里就开始有触礁的危险.
13.【答案】解:过A作于点E,
则米,米,
在中,,
则,
则;
在中,米,
米.
【解析】过A作于点E,可得米,米,在直角三角形中,利用锐角三角函数的定义求出,进一步求得的大小;
利用等腰直角三角形的性质求出DE的长,由求出CD的长即可.
此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解本题的关键.
14.【答案】解:如图,过点B作于点E,于点F,
,
易得四边形BEDF是矩形,
,,
在中,BE:::12,
设,,
根据勾股定理,得,
,
解得,
,
,
,
在中,,
米.
答:大楼的高度CD约为52米.
【解析】本题考查了解直角三角形的应用仰角俯角问题和坡度坡角问题,解决本题的关键是掌握仰角俯角和坡度坡角定义.
过点B作于点E,于点F,可得四边形BEDF是矩形,根据斜坡AB的坡度为:,设,,利用勾股定理可得x的值,再根据锐角三角函数即可进一步求大楼的高度CD.
15.【答案】解:如图示:过点C作,垂足为D,
由题意得,,,,
在中,米,
在中,,
米,
米.
答:桥AB的长度为米.
【解析】过点C作,垂足为D,根据在C处测得桥两端A,B两点的俯角分别为和,可得,,利用特殊角的三角函数求解即可.
本题考查了解直角三角形的应用,熟悉特殊角的三角函数值是解题的关键.
16.【答案】解:作于E,如图所示:
,
,,
由题意得:,
设,则,,
,
,
解得:,即,
又,
,
答:此时CD的长度约为.
【解析】本题考查了解直角三角形的应用;熟练掌握锐角三角函数的定义是解题的关键.
作于E,由直角三角形的性质得出,,由题意得:,设,则,,解直角三角形求出,即,再由锐角三角函数求出CD的长即可.
第4页,共16页
