万有引力理论的成就ppt
图片预览






文档简介
(共24张PPT)
1、内容:
3、适用条件: 质点或匀质球体
2、公式:
引力常量,由卡文迪许测出
①两质点间的距离
②均匀球体,球心间的距离
知识回顾
自然界中任何两个物体都相互吸引,引力
的大小与物体的质量m1和m2的乘积成正比,
与它们之间距离r的二次方成反比。
卡文迪许
“称量地球的质量”
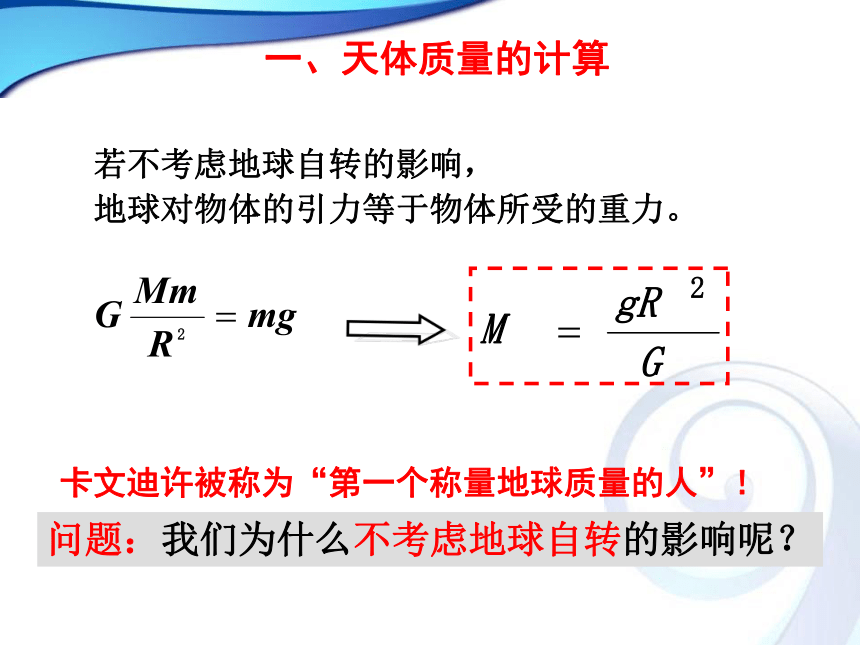
一、天体质量的计算
若不考虑地球自转的影响,
地球对物体的引力等于物体所受的重力。
卡文迪许被称为“第一个称量地球质量的人”!
问题:我们为什么不考虑地球自转的影响呢?
一、天体质量的计算
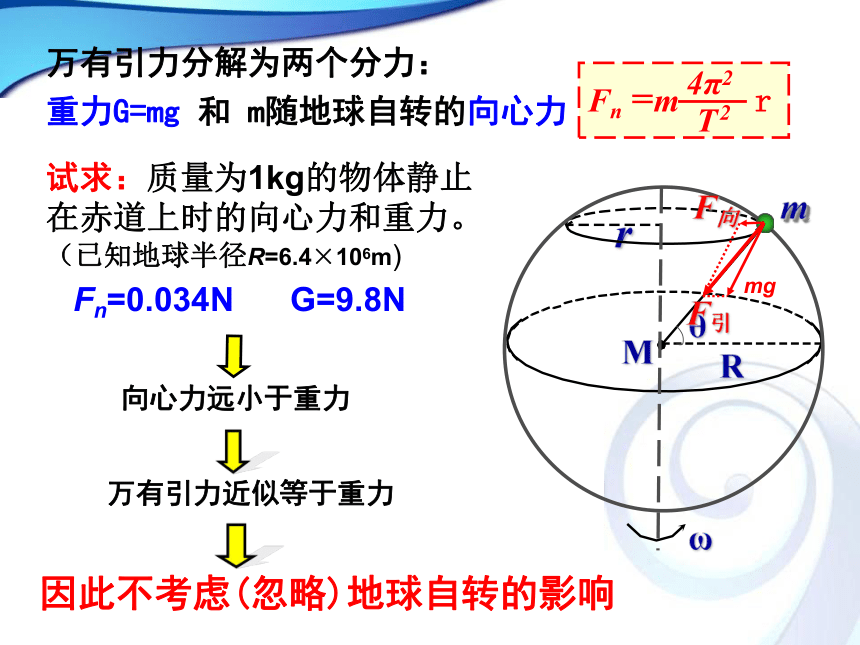
Fn=0.034N G=9.8N
万有引力分解为两个分力:
重力G=mg 和 m随地球自转的向心力
Fn =m r
4π2
T 2
因此不考虑(忽略)地球自转的影响
向心力远小于重力
万有引力近似等于重力
试求:质量为1kg的物体静止在赤道上时的向心力和重力。(已知地球半径R=6.4×106m)
R
M
θ
ω
r
m
F向
F引
mg
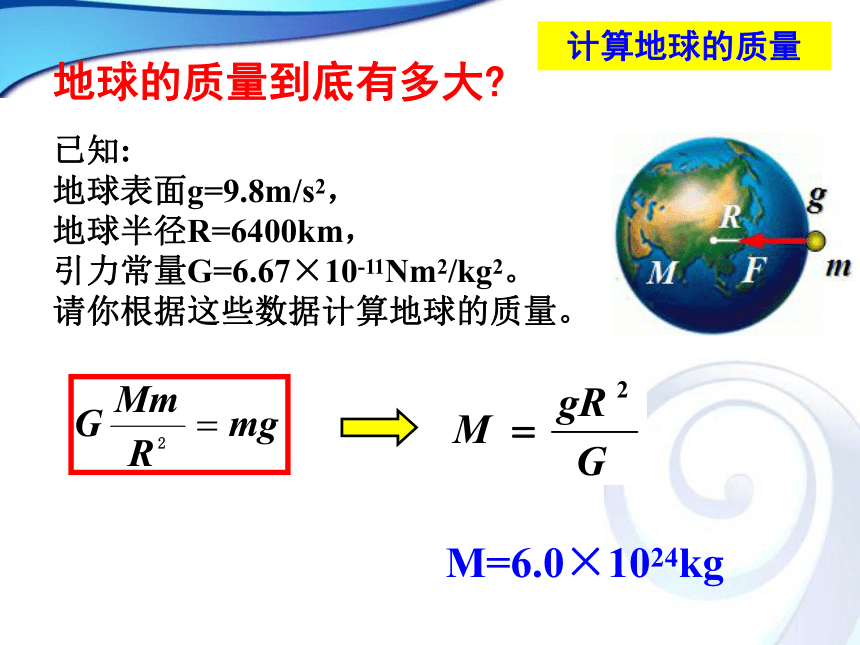
已知:
地球表面g=9.8m/s2,
地球半径R=6400km,
引力常量G=6.67×10-11Nm2/kg2。
请你根据这些数据计算地球的质量。
M=6.0×1024kg
地球的质量到底有多大
计算地球的质量
感叹
科学真是迷人啊!!根据零星的事实,增添一点猜想,竟能赢得那么多收获!
马克 吐温
用火箭把宇航员送到月球上,如果已知月球的半径,那么他用一个弹簧秤和一个已知质量的砝码,能否测出月球的质量?应该怎样测定?
小试一把
孩子们,你们能测出我的质量吗?
F引=Fn
已知火星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
1.将行星的运动看成是匀速圆周运动。
2.万有引力提供向心力 F引=Fn。
只能求出中心天体的质量!
不能求出环绕天体的质量!
计算太阳的质量
M
m
分析:
测出v和r
测出ω和r
测出T和r
F引=Fn
分析:
根据开普勒第三定律:
所以,上面的公式能保证这一点,而且我们还可以
知道常数K只和中心天体(太阳)的质量有关。
测出v和r
测出ω和r
测出T和r
F引=Fn
应用万有引力计算天体质量的基本思路:
1.确定中心天体,
找出绕该天体作匀速圆周运动的物体;
2.建立方程:
F引 = Fn
3.求解。
已知: 地球半径: R = 6400×103m
月亮周期: T = 27.3天≈2.36×106s
月亮轨道半径: r ≈ 60R,
求地球的质量M。
F引=Fn
计算地球的质量
M=6.0×1024kg
解:
法一:利用天体表面物体的万有引力等于重力
法二:利用环绕天体的物体,所受万有引力提供向心力
或
或
求天体质量的方法
表面型
环绕型
某行星表面附近有一颗卫星,其轨道半径可认为近似等于该行星的球体半径R。已测出此卫星运行的周期为T,已知万有引力常量为G。
求:
1.该行星的质量;
2.该行星的平均密度。
大试一把
二、天体密度的计算
若已知半径为R的球体体积的计算式为
则地球的平均密度表达式为 。
天体密度的计算
表面型 环绕型
天体质量
天体体积
密度公式
天体密度
一艘宇宙飞船贴近一行星表面飞行,测得它匀速圆周运动的周期为T,设万有引力常数G,则此行星的平均密度为为多大?
小试一把
作业:
书本课后1、2、3,晚上交。
作业本万有引力理论的成就(一)
1、内容:
3、适用条件: 质点或匀质球体
2、公式:
引力常量,由卡文迪许测出
①两质点间的距离
②均匀球体,球心间的距离
知识回顾
自然界中任何两个物体都相互吸引,引力
的大小与物体的质量m1和m2的乘积成正比,
与它们之间距离r的二次方成反比。
卡文迪许
“称量地球的质量”
一、天体质量的计算
若不考虑地球自转的影响,
地球对物体的引力等于物体所受的重力。
卡文迪许被称为“第一个称量地球质量的人”!
问题:我们为什么不考虑地球自转的影响呢?
一、天体质量的计算
Fn=0.034N G=9.8N
万有引力分解为两个分力:
重力G=mg 和 m随地球自转的向心力
Fn =m r
4π2
T 2
因此不考虑(忽略)地球自转的影响
向心力远小于重力
万有引力近似等于重力
试求:质量为1kg的物体静止在赤道上时的向心力和重力。(已知地球半径R=6.4×106m)
R
M
θ
ω
r
m
F向
F引
mg
已知:
地球表面g=9.8m/s2,
地球半径R=6400km,
引力常量G=6.67×10-11Nm2/kg2。
请你根据这些数据计算地球的质量。
M=6.0×1024kg
地球的质量到底有多大
计算地球的质量
感叹
科学真是迷人啊!!根据零星的事实,增添一点猜想,竟能赢得那么多收获!
马克 吐温
用火箭把宇航员送到月球上,如果已知月球的半径,那么他用一个弹簧秤和一个已知质量的砝码,能否测出月球的质量?应该怎样测定?
小试一把
孩子们,你们能测出我的质量吗?
F引=Fn
已知火星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
1.将行星的运动看成是匀速圆周运动。
2.万有引力提供向心力 F引=Fn。
只能求出中心天体的质量!
不能求出环绕天体的质量!
计算太阳的质量
M
m
分析:
测出v和r
测出ω和r
测出T和r
F引=Fn
分析:
根据开普勒第三定律:
所以,上面的公式能保证这一点,而且我们还可以
知道常数K只和中心天体(太阳)的质量有关。
测出v和r
测出ω和r
测出T和r
F引=Fn
应用万有引力计算天体质量的基本思路:
1.确定中心天体,
找出绕该天体作匀速圆周运动的物体;
2.建立方程:
F引 = Fn
3.求解。
已知: 地球半径: R = 6400×103m
月亮周期: T = 27.3天≈2.36×106s
月亮轨道半径: r ≈ 60R,
求地球的质量M。
F引=Fn
计算地球的质量
M=6.0×1024kg
解:
法一:利用天体表面物体的万有引力等于重力
法二:利用环绕天体的物体,所受万有引力提供向心力
或
或
求天体质量的方法
表面型
环绕型
某行星表面附近有一颗卫星,其轨道半径可认为近似等于该行星的球体半径R。已测出此卫星运行的周期为T,已知万有引力常量为G。
求:
1.该行星的质量;
2.该行星的平均密度。
大试一把
二、天体密度的计算
若已知半径为R的球体体积的计算式为
则地球的平均密度表达式为 。
天体密度的计算
表面型 环绕型
天体质量
天体体积
密度公式
天体密度
一艘宇宙飞船贴近一行星表面飞行,测得它匀速圆周运动的周期为T,设万有引力常数G,则此行星的平均密度为为多大?
小试一把
作业:
书本课后1、2、3,晚上交。
作业本万有引力理论的成就(一)
