7.3 频率与概率 2021-2022学年高一下学期 北师大版(2019)必修第一册(含答案)
文档属性
| 名称 | 7.3 频率与概率 2021-2022学年高一下学期 北师大版(2019)必修第一册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 18:45:15 | ||
图片预览


文档简介
7.3
频率与概率-2021-2022学年高一数学北师大版(2019)必修第一册同步课时作业
1.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是.用计算机生成了20组随机数,结果如下,若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是(
)
A.
B.
C.
D.
2.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物的消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:
满意情况
不满意
比较满意
满意
非常满意
人数
200
n
2100
1000
根据表中数据,估计在网上购物的消费者中对网上购物“比较满意”或“满意”的概率是(
)
A.
B.
C.
D.
3.袋子中有四个小球,分别写有“中、华、民、族”四个字,有放回地从中任取一个小球,直到“中”“华”两个字都取到才停止.用随机模拟的方法估计恰好抽取三次停止的概率,利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、华、民、族”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232
321
230
023
123
021
132
220
001
231
130
133
231
031
320
122
103
233
由此可以估计,恰好抽取三次就停止的概率为(
)
A.
B.
C.
D.
4.采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算机给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527
0293
7140
9857
0347
4373
8636
6947
1417
4698
0371
6233
2616
8045
6011
3661
9597
7424
7610
4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为(
)
A.0.852
B.0.8192
C.0.8
D.0.75
5.下列说法中正确的是(
)
A.任何事件的概率总是在之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
6.某种机器使用三年后即被淘汰,该机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个a元;在机器使用期间,如果备件不足再购买,则每个2a元.某人在购买该机器前,搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图.若以频率为概率,估计此人购机时购买20个备件,在机器淘汰时备件有剩余的概率为(
)
A.
B.
C.
D.
7.某厂产品的合格率为,估算该厂件产品中合格品的件数可能为(?
?).
A.160件??????B.7840件?????C.7998件?????D.7800件
8.有下列说法正确的是(
)
①频数和频率都能反映一个对象在试验总次数中出现的频繁程度;
②在同一次试验中,每个试验结果出现的频数之和等于试验的样本总数;
③在同一次试验中,每个试验结果出现的频率之和不一定等于1;
④概率就是频率.
A.①③
B.①②④
C.①②
D.③④
9.一个不透明的口袋中放有形状和大小相同的3个红球和1个白球,若从口袋中随机取出两个小球,则取到两个红球的概率为(
)
A.
B.
C.
D.
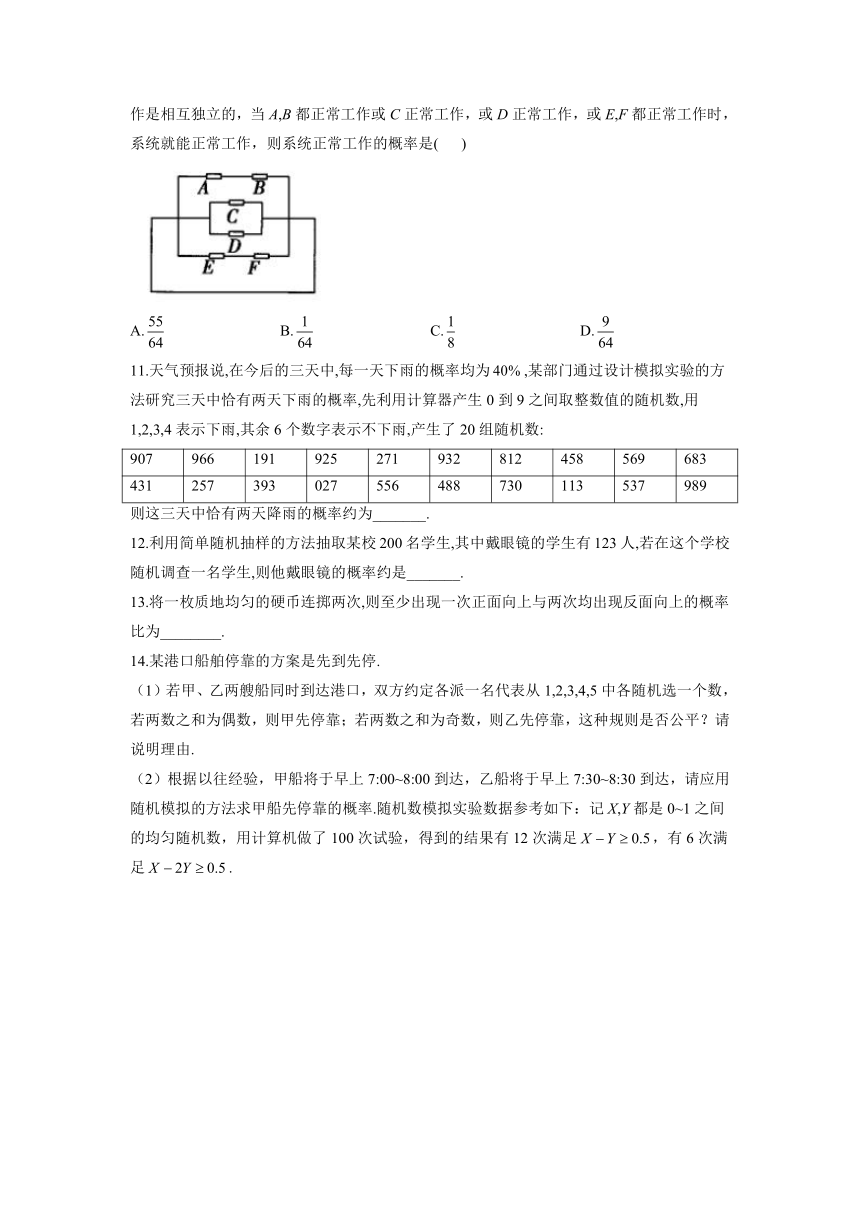
10.一个系统如图所示,A,B,C,D,E,F为6个部件,其正常工作的概率都是,且是否正常工作是相互独立的,当A,B都正常工作或C正常工作,或D正常工作,或E,F都正常工作时,系统就能正常工作,则系统正常工作的概率是(
)
A.
B.
C.
D.
11.天气预报说,在今后的三天中,每一天下雨的概率均为,某部门通过设计模拟实验的方法研究三天中恰有两天下雨的概率,先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,其余6个数字表示不下雨,产生了20组随机数:
907
966
191
925
271
932
812
458
569
683
431
257
393
027
556
488
730
113
537
989
则这三天中恰有两天降雨的概率约为_______.
12.利用简单随机抽样的方法抽取某校200名学生,其中戴眼镜的学生有123人,若在这个学校随机调查一名学生,则他戴眼镜的概率约是_______.
13.将一枚质地均匀的硬币连掷两次,则至少出现一次正面向上与两次均出现反面向上的概率比为________.
14.某港口船舶停靠的方案是先到先停.
(1)若甲、乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数,若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请应用随机模拟的方法求甲船先停靠的概率.随机数模拟实验数据参考如下:记X,Y都是0~1之间的均匀随机数,用计算机做了100次试验,得到的结果有12次满足,有6次满足.
答案以及解析
1.答案:A
解析:观察20个随机数,其中有116,812,730,
217,109,361,284,147,318,027共10个表示3天中恰有2天发布高温橙色预警信号,因此所求概率为,故选A.
2.答案:C
解析:由题意得,,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的总人数为,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的频率为.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为.故选C.
3.答案:C
解析:由随机模拟产生的随机数,可知恰好抽取三次就停止的有021,001,130,031,共4组随机数,可得恰好抽取三次就停止的概率约为,故选C.
4.答案:D
解析:因为射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,所以射击4次至少击中3次的概率为,故选D.
5.答案:C
解析:任何事件的概率总是在之间,其中必然事件的概率是1,不可能事件的概率是0,“任何事件”包含“必然事件”和“不可能事件”,故A错误.只有通过实验,才会得到频率的值,故频率不是客观存在的,一般来说,当试验的次数不同时,频率是不同的,它与试验次数有关,故B错误.当试验次数增多时,频率值会逐渐稳定于事件发生的概率,故C正确.概率是一个确定的值,它不是随机的,它是频率的稳定值,故D错误.故选C.
6.答案:B
解析:由频数分布直方图可知,机器在三年使用期内更换的易损零件数小于20的频率为,所以购机时购买20个备件,在机器淘汰时备件有剩余的概率约为.
7.答案:B
解析:由合格率的含义可知,
件产品中可能含有合格品
(件).
8.答案:C
解析:由频率、频数、概率的定义易知①②正确,故选C.
9.答案:B
解析:令红球为,白球为,取出两个小球的所有基本事件有、、、、、,共6个,其中满足条件的有3个,故所求概率为.
故选:B.
10.答案:A
解析:设“C正常工作”为事件G,“D正常工作”为事件H,“A与B中至少有一个不正常工作”为事件T,“E与F中至少有一个不正常工作”为事件R,则,,所以系统正常工作的概率.
11.答案:
解析:在20组随机数中表示三天中恰有两天下雨的有191,271,932,812,393,共有5组随机数,所以概率约为故答案为.
12.答案:0.615
解析:样本中的学生戴眼镜的频率为,
所以随机调查该校的一名学生,他戴眼镜的概率约为0.615.
13.答案:
解析:将一枚质地均匀的硬币连掷两次有以下情形:(正,正),(正,反),(反,正),(反,反).
至少出现—次正面向上有3种情形,两次均出现反面向上有1种情形,故答案为.
14.答案:(1)这种规则是不公平的.
理由如下:
设“甲先停靠”为事件A,“乙先停靠”为事件B.
两名代表从1,2,3,4,5中各随机选一个数的所有可能的结果为,,,,,,,,,,,,,,,,,,,,,,,,共25种,
其中两数之和为偶数所包含的结果为,,,,,,,,,,,,,共13种.
所以,,
所以这种规则不公平.
(2)应用随机模拟的方法,如果,即,
则甲船先停靠,
根据题意,100次试验有12次结果满足,
所以甲船先停靠的概率.
频率与概率-2021-2022学年高一数学北师大版(2019)必修第一册同步课时作业
1.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是.用计算机生成了20组随机数,结果如下,若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是(
)
A.
B.
C.
D.
2.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物的消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:
满意情况
不满意
比较满意
满意
非常满意
人数
200
n
2100
1000
根据表中数据,估计在网上购物的消费者中对网上购物“比较满意”或“满意”的概率是(
)
A.
B.
C.
D.
3.袋子中有四个小球,分别写有“中、华、民、族”四个字,有放回地从中任取一个小球,直到“中”“华”两个字都取到才停止.用随机模拟的方法估计恰好抽取三次停止的概率,利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、华、民、族”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232
321
230
023
123
021
132
220
001
231
130
133
231
031
320
122
103
233
由此可以估计,恰好抽取三次就停止的概率为(
)
A.
B.
C.
D.
4.采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算机给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527
0293
7140
9857
0347
4373
8636
6947
1417
4698
0371
6233
2616
8045
6011
3661
9597
7424
7610
4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为(
)
A.0.852
B.0.8192
C.0.8
D.0.75
5.下列说法中正确的是(
)
A.任何事件的概率总是在之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
6.某种机器使用三年后即被淘汰,该机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个a元;在机器使用期间,如果备件不足再购买,则每个2a元.某人在购买该机器前,搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图.若以频率为概率,估计此人购机时购买20个备件,在机器淘汰时备件有剩余的概率为(
)
A.
B.
C.
D.
7.某厂产品的合格率为,估算该厂件产品中合格品的件数可能为(?
?).
A.160件??????B.7840件?????C.7998件?????D.7800件
8.有下列说法正确的是(
)
①频数和频率都能反映一个对象在试验总次数中出现的频繁程度;
②在同一次试验中,每个试验结果出现的频数之和等于试验的样本总数;
③在同一次试验中,每个试验结果出现的频率之和不一定等于1;
④概率就是频率.
A.①③
B.①②④
C.①②
D.③④
9.一个不透明的口袋中放有形状和大小相同的3个红球和1个白球,若从口袋中随机取出两个小球,则取到两个红球的概率为(
)
A.
B.
C.
D.
10.一个系统如图所示,A,B,C,D,E,F为6个部件,其正常工作的概率都是,且是否正常工作是相互独立的,当A,B都正常工作或C正常工作,或D正常工作,或E,F都正常工作时,系统就能正常工作,则系统正常工作的概率是(
)
A.
B.
C.
D.
11.天气预报说,在今后的三天中,每一天下雨的概率均为,某部门通过设计模拟实验的方法研究三天中恰有两天下雨的概率,先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,其余6个数字表示不下雨,产生了20组随机数:
907
966
191
925
271
932
812
458
569
683
431
257
393
027
556
488
730
113
537
989
则这三天中恰有两天降雨的概率约为_______.
12.利用简单随机抽样的方法抽取某校200名学生,其中戴眼镜的学生有123人,若在这个学校随机调查一名学生,则他戴眼镜的概率约是_______.
13.将一枚质地均匀的硬币连掷两次,则至少出现一次正面向上与两次均出现反面向上的概率比为________.
14.某港口船舶停靠的方案是先到先停.
(1)若甲、乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数,若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请应用随机模拟的方法求甲船先停靠的概率.随机数模拟实验数据参考如下:记X,Y都是0~1之间的均匀随机数,用计算机做了100次试验,得到的结果有12次满足,有6次满足.
答案以及解析
1.答案:A
解析:观察20个随机数,其中有116,812,730,
217,109,361,284,147,318,027共10个表示3天中恰有2天发布高温橙色预警信号,因此所求概率为,故选A.
2.答案:C
解析:由题意得,,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的总人数为,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的频率为.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为.故选C.
3.答案:C
解析:由随机模拟产生的随机数,可知恰好抽取三次就停止的有021,001,130,031,共4组随机数,可得恰好抽取三次就停止的概率约为,故选C.
4.答案:D
解析:因为射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,所以射击4次至少击中3次的概率为,故选D.
5.答案:C
解析:任何事件的概率总是在之间,其中必然事件的概率是1,不可能事件的概率是0,“任何事件”包含“必然事件”和“不可能事件”,故A错误.只有通过实验,才会得到频率的值,故频率不是客观存在的,一般来说,当试验的次数不同时,频率是不同的,它与试验次数有关,故B错误.当试验次数增多时,频率值会逐渐稳定于事件发生的概率,故C正确.概率是一个确定的值,它不是随机的,它是频率的稳定值,故D错误.故选C.
6.答案:B
解析:由频数分布直方图可知,机器在三年使用期内更换的易损零件数小于20的频率为,所以购机时购买20个备件,在机器淘汰时备件有剩余的概率约为.
7.答案:B
解析:由合格率的含义可知,
件产品中可能含有合格品
(件).
8.答案:C
解析:由频率、频数、概率的定义易知①②正确,故选C.
9.答案:B
解析:令红球为,白球为,取出两个小球的所有基本事件有、、、、、,共6个,其中满足条件的有3个,故所求概率为.
故选:B.
10.答案:A
解析:设“C正常工作”为事件G,“D正常工作”为事件H,“A与B中至少有一个不正常工作”为事件T,“E与F中至少有一个不正常工作”为事件R,则,,所以系统正常工作的概率.
11.答案:
解析:在20组随机数中表示三天中恰有两天下雨的有191,271,932,812,393,共有5组随机数,所以概率约为故答案为.
12.答案:0.615
解析:样本中的学生戴眼镜的频率为,
所以随机调查该校的一名学生,他戴眼镜的概率约为0.615.
13.答案:
解析:将一枚质地均匀的硬币连掷两次有以下情形:(正,正),(正,反),(反,正),(反,反).
至少出现—次正面向上有3种情形,两次均出现反面向上有1种情形,故答案为.
14.答案:(1)这种规则是不公平的.
理由如下:
设“甲先停靠”为事件A,“乙先停靠”为事件B.
两名代表从1,2,3,4,5中各随机选一个数的所有可能的结果为,,,,,,,,,,,,,,,,,,,,,,,,共25种,
其中两数之和为偶数所包含的结果为,,,,,,,,,,,,,共13种.
所以,,
所以这种规则不公平.
(2)应用随机模拟的方法,如果,即,
则甲船先停靠,
根据题意,100次试验有12次结果满足,
所以甲船先停靠的概率.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
