2021-2022学年苏科版七年级数学上册 2.1-2.4期中复习课件(15张ppt)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学上册 2.1-2.4期中复习课件(15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
§2.1~2.4
复习
在前面几节课里,学习了哪些知识?
冰箱冷藏室的温度零上
5
℃记作
+5
℃,冷冻室的温度零下
7
℃记作(
)
A.
+7
℃
B.
-2
℃
C.
-12
℃
D.
-7
℃
相反意义
正数负数
定义
表示
读法
用正数、负数表示相反意义的量
D
下列各数:-3.14,
,0.2020020002,+3,
,有理数有(
)
A.
1个
B.
2个
C.
3个
D.
4个
D
有理数
整数
分数
正整数
零
负整数
正分数
负分数
正有理数
负有理数
零
正整数
正分数
负整数
负分数
有理数与无理数
下列四个数中,无理数是(
)
A.-3.1415926
B.
C.
5.050050005…
D.
0
C
无理数:无限不循环小数
小数
有限小数
无限小数
分数
无限循环小数
分数
无限不循环小数
无理数
有理数
有理数
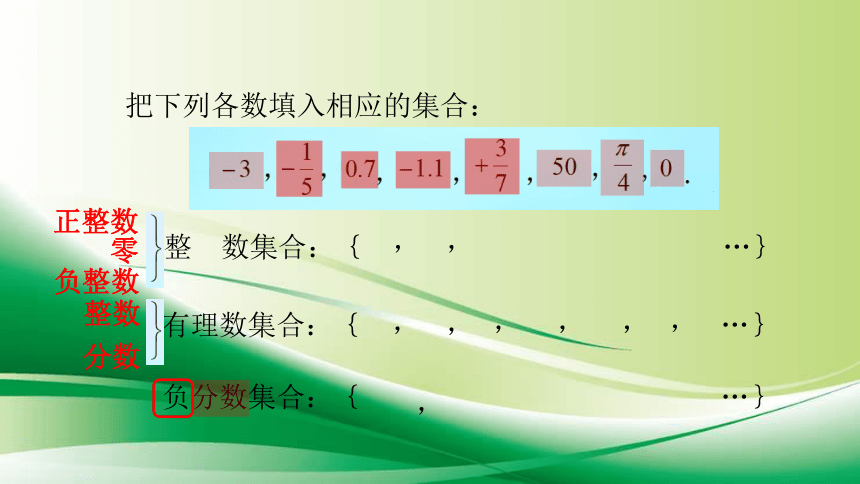
把下列各数填入相应的集合:
整
数集合:{
…}
有理数集合:{
…}
负分数集合:{
…}
正整数
负整数
零
整数
分数
,
,
,
,
,
,
,
,
,
在数轴上画出表示下列各数的点:
-3,-1.5,0,1.
数轴:规定了原点、正方向、单位长度的直线.
数轴的定义
0
1
2
3
-1
-2
-3
-3
-1.5
0
1
有理数和无理数都可以用数轴上的点表示,
数轴上任意一点都表示一个无理数或有理数.
在数轴上表示的两个数,右边的数总比左边的数大.
-3<-1.5<0<1
若
,则
的值为(
)
A.
3
B.
-3
C.
±3
D.
A
绝对值与相反数
绝对值:数轴上表示这个数的点与原点的距离.
数轴上与原点的距离小于4的整数的点有____个.
0
1
2
3
-1
-2
-3
4
-4
7
定义
表示
读法
-(-5)=______,-(-5)是_______的相反数;
-(+4)是_______的相反数,-(+4)=______;
+(+3)=______,+(-3)=______.
判断:带“-”号的数一定是负数.(
)
-5
5
表示一个数的相反数,在这个数前面添“-”号.
4
-4
3
-3
×
符号不同、绝对值相同的两个数互为相反数.
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
比较
-3
与
-1.5
的大小.
0
1
-1
-2
-3
-3
-1.5
解:
所以
-3<-1.5
解:因为
,
且
所以
-3<-1.5
1.若A是数轴上一点,点A表示的数是
-2
,把点A向左移动3个单位长度后,再向右移动1个单位长度,这时它表示的数是________.
-4
探索活动
0
1
2
-4
-1
-2
-3
-5
A
0
1
2
-4
-1
-2
-3
-5
2.若A、B是数轴上的两个点,点A表示的数是-2,点B与点A的距离是3,则点B表示的数是________.
A
B
B
1或-5
探索活动
3
3
3.如图,数轴上点A、B之间的距离是4个单位长度,它们表示的数互为相反数,则点C表示的数是______.
A
B
C
0
2
2
?
-4
探索活动
0
1
2
3
4
-3
-2
-1
4.直径为1个单位长度的圆上有一点A与数轴的原点重合.
(1)把圆沿数轴向右滚动1周,点A到达数轴上的位置记为点B,则点B表示的数是________,它是有理数吗?
A
探索活动
本节课有什么收获?
有理数
整数
分数
正整数
零
负整数
正分数
负分数
无理数:无限不循环小数.
数轴是工具
?
绝对值、相反数
§2.1~2.4
复习
在前面几节课里,学习了哪些知识?
冰箱冷藏室的温度零上
5
℃记作
+5
℃,冷冻室的温度零下
7
℃记作(
)
A.
+7
℃
B.
-2
℃
C.
-12
℃
D.
-7
℃
相反意义
正数负数
定义
表示
读法
用正数、负数表示相反意义的量
D
下列各数:-3.14,
,0.2020020002,+3,
,有理数有(
)
A.
1个
B.
2个
C.
3个
D.
4个
D
有理数
整数
分数
正整数
零
负整数
正分数
负分数
正有理数
负有理数
零
正整数
正分数
负整数
负分数
有理数与无理数
下列四个数中,无理数是(
)
A.-3.1415926
B.
C.
5.050050005…
D.
0
C
无理数:无限不循环小数
小数
有限小数
无限小数
分数
无限循环小数
分数
无限不循环小数
无理数
有理数
有理数
把下列各数填入相应的集合:
整
数集合:{
…}
有理数集合:{
…}
负分数集合:{
…}
正整数
负整数
零
整数
分数
,
,
,
,
,
,
,
,
,
在数轴上画出表示下列各数的点:
-3,-1.5,0,1.
数轴:规定了原点、正方向、单位长度的直线.
数轴的定义
0
1
2
3
-1
-2
-3
-3
-1.5
0
1
有理数和无理数都可以用数轴上的点表示,
数轴上任意一点都表示一个无理数或有理数.
在数轴上表示的两个数,右边的数总比左边的数大.
-3<-1.5<0<1
若
,则
的值为(
)
A.
3
B.
-3
C.
±3
D.
A
绝对值与相反数
绝对值:数轴上表示这个数的点与原点的距离.
数轴上与原点的距离小于4的整数的点有____个.
0
1
2
3
-1
-2
-3
4
-4
7
定义
表示
读法
-(-5)=______,-(-5)是_______的相反数;
-(+4)是_______的相反数,-(+4)=______;
+(+3)=______,+(-3)=______.
判断:带“-”号的数一定是负数.(
)
-5
5
表示一个数的相反数,在这个数前面添“-”号.
4
-4
3
-3
×
符号不同、绝对值相同的两个数互为相反数.
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数小.
比较
-3
与
-1.5
的大小.
0
1
-1
-2
-3
-3
-1.5
解:
所以
-3<-1.5
解:因为
,
且
所以
-3<-1.5
1.若A是数轴上一点,点A表示的数是
-2
,把点A向左移动3个单位长度后,再向右移动1个单位长度,这时它表示的数是________.
-4
探索活动
0
1
2
-4
-1
-2
-3
-5
A
0
1
2
-4
-1
-2
-3
-5
2.若A、B是数轴上的两个点,点A表示的数是-2,点B与点A的距离是3,则点B表示的数是________.
A
B
B
1或-5
探索活动
3
3
3.如图,数轴上点A、B之间的距离是4个单位长度,它们表示的数互为相反数,则点C表示的数是______.
A
B
C
0
2
2
?
-4
探索活动
0
1
2
3
4
-3
-2
-1
4.直径为1个单位长度的圆上有一点A与数轴的原点重合.
(1)把圆沿数轴向右滚动1周,点A到达数轴上的位置记为点B,则点B表示的数是________,它是有理数吗?
A
探索活动
本节课有什么收获?
有理数
整数
分数
正整数
零
负整数
正分数
负分数
无理数:无限不循环小数.
数轴是工具
?
绝对值、相反数
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
