2020-2021学年北师大版数学九年级下册3.4 圆周角与圆心角的关系 课件(共22张PPT)
文档属性
| 名称 | 2020-2021学年北师大版数学九年级下册3.4 圆周角与圆心角的关系 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
北师大版九年级下册第三章《圆》
3.4
圆周角与圆心角的关系(1)
学习目标:理解圆周角定义,掌握圆周角定理,并
能运用定理及推论解决简单的几何问题.
学习重点:圆周角定理及其应用.
学习难点:圆周角定理证明过程中“分类讨论”
思想的渗透.
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
小明
小强
情境问题
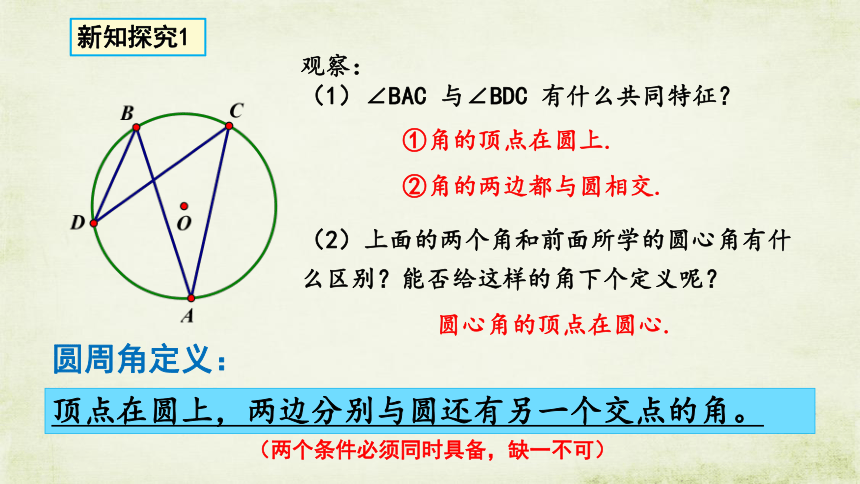
顶点在圆上,两边分别与圆还有另一个交点的角。
观察:
(1)∠BAC
与∠BDC
有什么共同特征?
(2)上面的两个角和前面所学的圆心角有什么区别?能否给这样的角下个定义呢?
①角的顶点在圆上.
②角的两边都与圆相交.
圆心角的顶点在圆心.
新知探究1
圆周角定义:
(两个条件必须同时具备,缺一不可)
1.判别下列各图形中的角是不是圆周角,并说明理由。
×
√
×
×
×
×
2.指出图中的圆周角.
∠BAC
∠CAO
∠BAO
∠CBO
∠CBA
∠ABO
∠ACO
∠BCA
∠BCO
练习巩固
一条边没有和圆相交
圆心角
顶点不在圆上
顶点不在圆上
两条边没有和圆相交
O
A
C
B
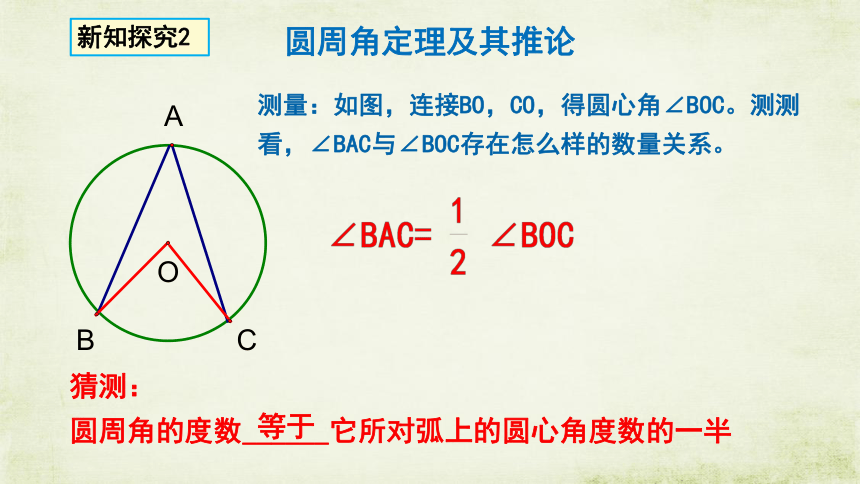
新知探究2
圆周角定理及其推论
测量:如图,连接BO,CO,得圆心角∠BOC。测测看,∠BAC与∠BOC存在怎么样的数量关系。
猜测:
圆周角的度数______它所对弧上的圆心角度数的一半
等于
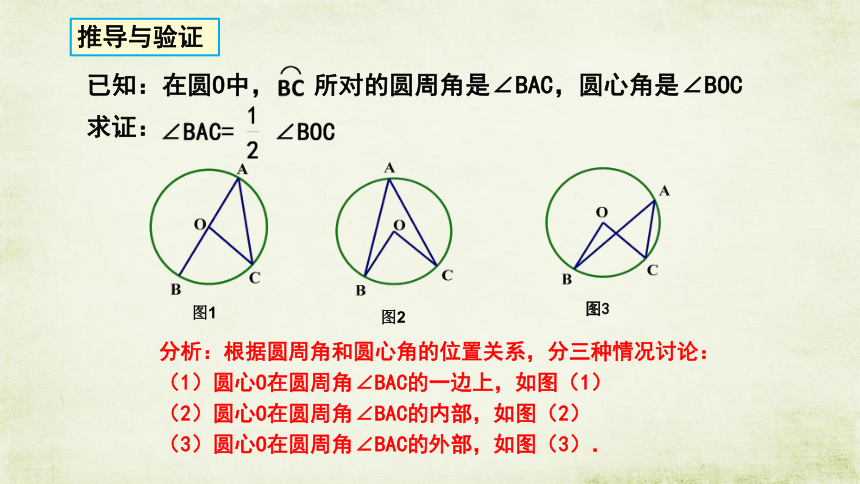
推导与验证
分析:根据圆周角和圆心角的位置关系,分三种情况讨论:
(1)圆心O在圆周角∠BAC的一边上,如图(1)
(2)圆心O在圆周角∠BAC的内部,如图(2)
(3)圆心O在圆周角∠BAC的外部,如图(3).
图2
图1
图3
已知:在圆O中,
所对的圆周角是∠BAC,圆心角是∠BOC
求证:
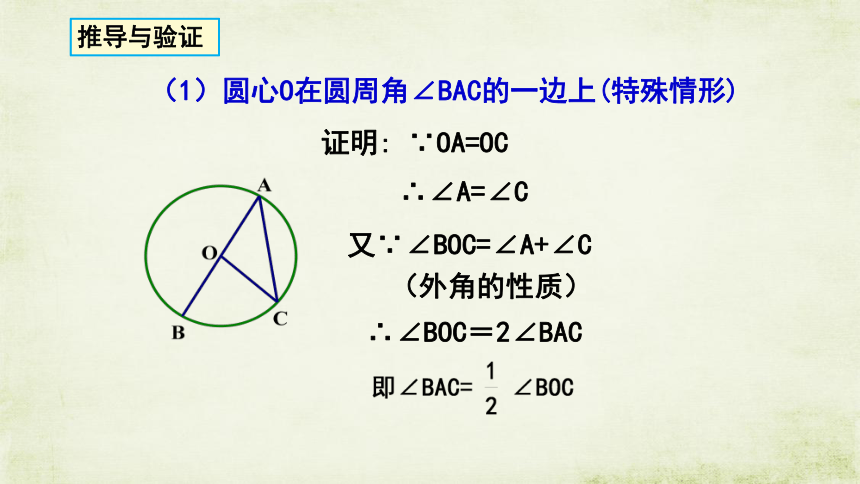
(1)圆心O在圆周角∠BAC的一边上(特殊情形)
证明:
∵OA=OC
∴∠A=∠C
又∵∠BOC=∠A+∠C
(外角的性质)
∴∠BOC=2∠BAC
推导与验证
D
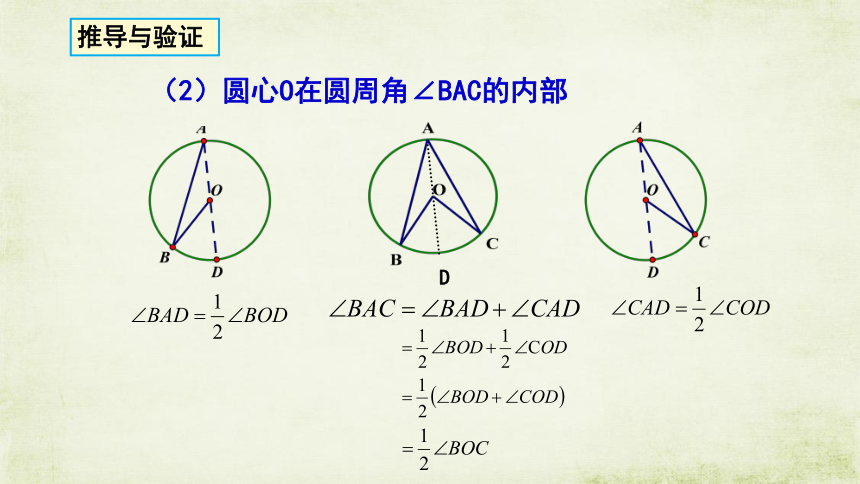
推导与验证
(2)圆心O在圆周角∠BAC的内部
推导与验证
(3)圆心O在圆周角∠BAC的外部
D
O
要点归纳
圆周角定理及其推论
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半
推论1:
同弧所对的圆周角相等。
A
A1
A2
A3
A4
B
C
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
小明
小强
情境问题解决
∠BAC
=
∠BDC
1、如图1,点A、B、C、D在⊙O上,点A、D在点B、C所在直线的同侧,∠BAC=35°,则
∠BDC
=
,理由是
;
∠BOC
=
,
理由是
.
70°
35°
同弧所对的圆周角相等
圆周角的度数等于它所对弧上圆心角度数的一半
图1
2、如图2,圆中相等的圆周角有
.
∠A=∠D、∠B=∠C
图2
练习巩固
3、如图,点A、B、C、D在⊙O上,AC、BD为四边形ABCD的对角线
∠1=
∠2=
∠3=
∠5=
∠4
∠7
∠6
∠8
4、如图,在⊙O
中
=
,那么∠C
和∠G
的大小有什么关系?
O
F
B
A
C
E
G
∵∠AOB=∠EOF
圆周角定理的推论:
同弧或等弧所对的圆周角相等。
∴∠C=∠G
典例分析
圆周角定理及其推论的应用
例1、如图,OA、OB、OC是⊙O的半径∠AOB=70°∠BOC=30°,求∠ACB和∠BAC度数
解析:
∵圆心角∠AOB与圆周角∠ACB对的弧为
⌒AB
典例分析
圆周角定理及其推论的应用
例2、如图,AB是⊙O的直径,C、D、E都是圆上的点,
则∠1+∠2=
______
90°
例3、如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是(
)
A.15°
B.25°
C.30°
D.75°
典例分析
圆周角定理及其推论的应用
解析:由圆周角定理的推论可知:
∠B=∠C
又∵∠AMD=∠A+∠C
(外角的性质)
∴∠B=∠C=∠AMD-∠A
=75°-45°=30°
C
典例分析
圆周角定理及其推论的应用
例4、如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5°
B.15°
C.20°
D.22.5°
B
数学
知识
数学
方法
转化
化转
圆周角的概念
圆周角定理及推论
分类讨论
思想
转化
思想
课堂小结
顶点在圆上,两边分别与圆还有另一个交点的角
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半
圆周角定理的推论:
同弧或等弧所对的圆周角相等。
圆周角和圆心角的关系
课后巩固
1、判断正误:
(1)同一个圆中等弧所对的圆周角相等
(
)
(2)相等的弦所对的圆周角也相等
(
)
(3)同弦所对的圆周角相等
(
)
2、如图,已知:⊙O是△ABC的外接圆,∠BAC=50°,∠ABC=47°,求∠A0B=_______.
3、如图3,已知圆心角∠AOB=100°,求圆周角∠ACB=_______
A
O
B
C
4、如图4,⊙O是△ABC的外接圆,∠C=30°,AB=2,则∠AOB=______,⊙O的半径是_____,
图3
图4
谢
谢!
北师大版九年级下册第三章《圆》
3.4
圆周角与圆心角的关系(1)
学习目标:理解圆周角定义,掌握圆周角定理,并
能运用定理及推论解决简单的几何问题.
学习重点:圆周角定理及其应用.
学习难点:圆周角定理证明过程中“分类讨论”
思想的渗透.
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
小明
小强
情境问题
顶点在圆上,两边分别与圆还有另一个交点的角。
观察:
(1)∠BAC
与∠BDC
有什么共同特征?
(2)上面的两个角和前面所学的圆心角有什么区别?能否给这样的角下个定义呢?
①角的顶点在圆上.
②角的两边都与圆相交.
圆心角的顶点在圆心.
新知探究1
圆周角定义:
(两个条件必须同时具备,缺一不可)
1.判别下列各图形中的角是不是圆周角,并说明理由。
×
√
×
×
×
×
2.指出图中的圆周角.
∠BAC
∠CAO
∠BAO
∠CBO
∠CBA
∠ABO
∠ACO
∠BCA
∠BCO
练习巩固
一条边没有和圆相交
圆心角
顶点不在圆上
顶点不在圆上
两条边没有和圆相交
O
A
C
B
新知探究2
圆周角定理及其推论
测量:如图,连接BO,CO,得圆心角∠BOC。测测看,∠BAC与∠BOC存在怎么样的数量关系。
猜测:
圆周角的度数______它所对弧上的圆心角度数的一半
等于
推导与验证
分析:根据圆周角和圆心角的位置关系,分三种情况讨论:
(1)圆心O在圆周角∠BAC的一边上,如图(1)
(2)圆心O在圆周角∠BAC的内部,如图(2)
(3)圆心O在圆周角∠BAC的外部,如图(3).
图2
图1
图3
已知:在圆O中,
所对的圆周角是∠BAC,圆心角是∠BOC
求证:
(1)圆心O在圆周角∠BAC的一边上(特殊情形)
证明:
∵OA=OC
∴∠A=∠C
又∵∠BOC=∠A+∠C
(外角的性质)
∴∠BOC=2∠BAC
推导与验证
D
推导与验证
(2)圆心O在圆周角∠BAC的内部
推导与验证
(3)圆心O在圆周角∠BAC的外部
D
O
要点归纳
圆周角定理及其推论
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半
推论1:
同弧所对的圆周角相等。
A
A1
A2
A3
A4
B
C
足球训练场上教练在球门前划了一个圆圈,进行无人防守的射门训练,如图,小明、小强两名同学分别站在圆上A、D两地,他们争论不休,都说自己所在位置,射门角度大,射门的机率高。如果你是教练,请评一评他们两个人,如果仅从射门角度的大小考虑,谁的位置射门更有利?
A
D
B
C
O
小明
小强
情境问题解决
∠BAC
=
∠BDC
1、如图1,点A、B、C、D在⊙O上,点A、D在点B、C所在直线的同侧,∠BAC=35°,则
∠BDC
=
,理由是
;
∠BOC
=
,
理由是
.
70°
35°
同弧所对的圆周角相等
圆周角的度数等于它所对弧上圆心角度数的一半
图1
2、如图2,圆中相等的圆周角有
.
∠A=∠D、∠B=∠C
图2
练习巩固
3、如图,点A、B、C、D在⊙O上,AC、BD为四边形ABCD的对角线
∠1=
∠2=
∠3=
∠5=
∠4
∠7
∠6
∠8
4、如图,在⊙O
中
=
,那么∠C
和∠G
的大小有什么关系?
O
F
B
A
C
E
G
∵∠AOB=∠EOF
圆周角定理的推论:
同弧或等弧所对的圆周角相等。
∴∠C=∠G
典例分析
圆周角定理及其推论的应用
例1、如图,OA、OB、OC是⊙O的半径∠AOB=70°∠BOC=30°,求∠ACB和∠BAC度数
解析:
∵圆心角∠AOB与圆周角∠ACB对的弧为
⌒AB
典例分析
圆周角定理及其推论的应用
例2、如图,AB是⊙O的直径,C、D、E都是圆上的点,
则∠1+∠2=
______
90°
例3、如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是(
)
A.15°
B.25°
C.30°
D.75°
典例分析
圆周角定理及其推论的应用
解析:由圆周角定理的推论可知:
∠B=∠C
又∵∠AMD=∠A+∠C
(外角的性质)
∴∠B=∠C=∠AMD-∠A
=75°-45°=30°
C
典例分析
圆周角定理及其推论的应用
例4、如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5°
B.15°
C.20°
D.22.5°
B
数学
知识
数学
方法
转化
化转
圆周角的概念
圆周角定理及推论
分类讨论
思想
转化
思想
课堂小结
顶点在圆上,两边分别与圆还有另一个交点的角
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半
圆周角定理的推论:
同弧或等弧所对的圆周角相等。
圆周角和圆心角的关系
课后巩固
1、判断正误:
(1)同一个圆中等弧所对的圆周角相等
(
)
(2)相等的弦所对的圆周角也相等
(
)
(3)同弦所对的圆周角相等
(
)
2、如图,已知:⊙O是△ABC的外接圆,∠BAC=50°,∠ABC=47°,求∠A0B=_______.
3、如图3,已知圆心角∠AOB=100°,求圆周角∠ACB=_______
A
O
B
C
4、如图4,⊙O是△ABC的外接圆,∠C=30°,AB=2,则∠AOB=______,⊙O的半径是_____,
图3
图4
谢
谢!
