2.1整式课件 2021—2022学年人教版数学七年级上册(第一课时 31张)
文档属性
| 名称 | 2.1整式课件 2021—2022学年人教版数学七年级上册(第一课时 31张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 08:30:34 | ||
图片预览











文档简介
(共31张PPT)
第二章
整式的加减
2.1
整式
第一课时
【学习目标】
准确理解用字母表示数的意义。
掌握用字母表示数和数量关系的规律和方法。
培养观察、分析、抽象、概括等思维能力和应用意识。
【课前预习】
1.一种商品进价为每件a元,按进价增加25%出售,则增加后的售价为每件(
)元.
A.0.25a
B.0.75a
C.1.25a
D.a+25%
2.下列说法错误的是(
)
A.2m是2个数m的和B.2m是2和数m的积C.2m是单项式D.2m+1是奇数
3.《九章算术》中记载一同题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?设有x人,则表示物价的代数式可以是(
)
A.8x-3
B.8x+3
C.7x-4
D.7(x+4)
4.用字母表示数,下列书写规范的是( )
A.a?
B.-1x
C.1
a
D.2a?
5.一双鞋先降价20%,又涨价20%,现在价格与原价相比(
).
A.现价高
B.原价高
C.与原价相等
D.无法比较
【课前预习】答案
1.C
2.D
3.A
4.D
5.B
1.K先生正在看《阿Q正传》,这里K、Q表示什么?
2.从A地到B地要走3个小时.这里A、B表示什么?
字母可表示:人名
3.加法交换律:
a+b=b+a
字母可表示:地名
字母可表示:运算定律
生活中的字母
导入新课
【学习探究】
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100
km/h.根据已知数据求出列车在冻土地段行驶的路程.
(1)2
h行驶多少千米?3
h呢?8
h呢?t
h呢?
(2)字母t表示时间有什么意义?
如果用v表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
怎样分析数量关系,并用含有字母的式子表示数量关系呢?
(2)绕地球飞行n周,约需90n
分钟
解:
问题1:中国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.它在椭圆形轨道上环绕地球飞过1周,约需90分钟.试求:
(1)
绕地球飞行10周约需多少分钟?
(2)绕地球飞行n周约需多少分钟?
(1)绕地球飞行10周,约需90×10=900
(分钟)
含字母的式子的书写
一
问题2:像0,±2,±4,±6,…能被2整除的数叫做偶数;像±1,
±3,±5,…不能被2整除的数叫做奇数.
如果k表示一个整数,那么偶数表示为
____
,奇数表示为
____
.
整数
…
-3
-2
-1
0
1
2
3
…
k
…
偶数
…
-6
-4
-2
0
2
4
6
…
____
…
奇数
…
-7
-5
-3
-1
1
3
5
…
____
…
2k
2k-1
2k-1
2k
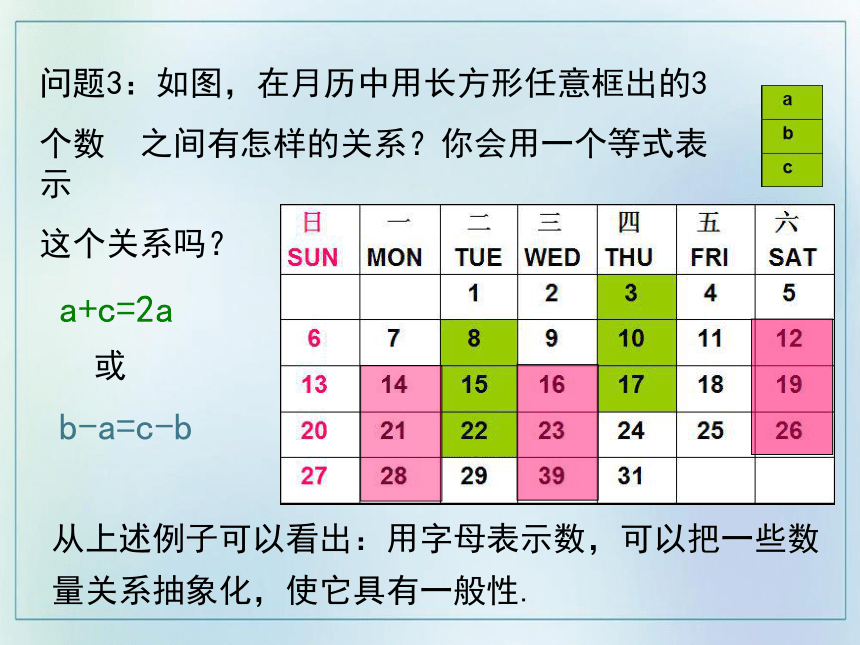
问题3:如图,在月历中用长方形任意框出的3
个数
之间有怎样的关系?你会用一个等式表示
这个关系吗?
a+c=2a
或
b-a=c-b
从上述例子可以看出:用字母表示数,可以把一些数量关系抽象化,使它具有一般性.
用含有字母的式子表示下列数量
例1
(2)练习簿的单价为b
元,
a本练习簿的总价是
元.
(1)练习簿的单价为a元,100本练习簿的总价是
元.
②字母和字母相乘,乘号可以省略不写或用“
·
”
表示.
一般情况下,按26个字母的顺序从左到右来写.
100a
ab
①数和字母相乘,可省略乘号,并把数字写在字母的前面
(3)练习簿的单价为0.5元,圆珠笔的单价是3.2元,
买a本练习簿和b支笔的总价是
元.
③后面带单位的相加或相减的式子要用括号括起来
(0.5a+3.2b)
④除法运算写成分数形式,即除号改为分数线
(4)小明的家离学校s千米,小明骑车上学.若每小时行
10千米,则需
时.
⑤带分数与字母相乘时,带分数要写成假分数的形式
(5)若每斤苹果
元,则买m斤苹果需
元.
(6)姚明个子高,经测量他通常跨一步的距离1米,
若取向前为正,向后为负,那么姚明向前跨
a步为
米,向后跨a步为
米.
a
-a
6.当“1”与任何字母相乘时,“1”省略不写;
当“-1”乘以字母时,只要在那个字母前加上“-”号.
1×a=a
;
(-1)×a=-a
例2(1)一条河的水流速度是2.5
km/h,船在静水中的速度是
v
km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
分析:船在河流中行驶时,船的速度需要分两种情况讨论:
顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是
km/h,逆水行驶的速度是
km/h.
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要
z
元,用式子表示买
3个篮球、5个排球、2个足球共需要的钱数;
解:(2)买3个篮球、5个排球、2个足球共需要
元.
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2
)是
.
(4)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
解:(4)这所住宅的建筑面积(单位:m2)是
.
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳:
强调:
在含有字母的式子中如果出现乘号,通常将乘号写作“·”或省略不写.例如,100×t可以写成100
·t或100t.
归纳:
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
运算定律
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a
+
b
=
b
+
a
(a
+
b)
+c=
a
+(b
+
c)
ab
=
ba
(ab)c
=
a(bc)
(a
+
b)
c
=
ac+bc
1.用字母表示数的运算律
用字母表示运算律和公式
例3
(1)小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍,
则亮亮的速度可以表示为____米/秒.
(2)如图,
用字母表示图中阴影
部分的面积是_________
m
n
p
q
3v
一个正方形盒子的棱长为acm,用含a的式子表示:
盒子的表面积S=____________;
盒子的体积V=____________.
(1)买一个篮球需要x元,买一个排球需要y元,买一个足球需要
z
元,用式子表示买
3个篮球、5个排球、2个足球共需要的钱数。
例4
用含字母的式子表示数量关系
解:买3个篮球、5个排球、2个足球共需要
元.
1.我们现在讨论的数的范围是有理数,即数a可以是正数,也可以是负数或零,所以a不一定表示正数,-a不一定表示负数.
2.同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
注意:
(1)某种商品每袋4.8元,在一个月内的销售量是m
袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是
r,h,用式子表示圆柱体的体积.
【课后练习】
1.某服装店新开张,第一天销售服装a件,第二天比第一天多销售5件,第三天的销售量是第二天的3倍少9件,则第三天销售了( )
A.(3a+6)件
B.(3a+15)件
C.(3a+9)件
D.(3a+24)件
2.下列说法中,正确的个数有
(
)
个.
①
有理数包括整数和分数;
②
一个代数式不是单项式就是多项式;③
几个有理数相乘,若负因数的个数是偶数个,则积为正数.
④
倒数等于本身的数有1,-l;
A.1
B.2
C.3
D.4
3.下列式子符合书写要求的是( )
A.-xy?
B.a-1÷b
C.4xy
D.ab×3
4.对于代数式(a+b)?,下列描述正确的是( )
A.a与b?的平方的和B.a与b的平方和C.a与b的和的平方D.a与b的平方的和
5.一个两位数的个位上的数是a,十位上的数是b,则这个两位数表示为(
)
A.A+b
B.10a+b
C.a+10b
D.ba
6.一台电脑按原价的85%出售,每台售价为y元,则这台电脑原价为______.
7.a、b两数差的5倍,用代数式可表示为_________________.
8.某校七年级有师生参加爱心捐款活动,其中有a名教师,b名学生,若平均每名教师捐x元,每名学生捐10元,则他们一共捐款___________元.
9.观察下列算式:①3?-1?=8,②5?-3?=16,③7?-5?=24,④9?-7?=32,…,请用你发现的规律将第n个式子表示出来:______________________________.
10.甲,乙两人分别从两地同时出发,若相向而行,则a小时相遇;若同向而行,则b小时甲追上乙,那么甲的速度是乙的速度的_______.
【课后练习】答案
1.、A
2.B
3.A
4.C
5.C
【课后练习】
1.C
2.D
3.A
4.D
5.B
6.
7.5(a-b)
8.(ax+10b)
9.(2n+1)2-(2n-1)2=8n
10.
第二章
整式的加减
2.1
整式
第一课时
【学习目标】
准确理解用字母表示数的意义。
掌握用字母表示数和数量关系的规律和方法。
培养观察、分析、抽象、概括等思维能力和应用意识。
【课前预习】
1.一种商品进价为每件a元,按进价增加25%出售,则增加后的售价为每件(
)元.
A.0.25a
B.0.75a
C.1.25a
D.a+25%
2.下列说法错误的是(
)
A.2m是2个数m的和B.2m是2和数m的积C.2m是单项式D.2m+1是奇数
3.《九章算术》中记载一同题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?设有x人,则表示物价的代数式可以是(
)
A.8x-3
B.8x+3
C.7x-4
D.7(x+4)
4.用字母表示数,下列书写规范的是( )
A.a?
B.-1x
C.1
a
D.2a?
5.一双鞋先降价20%,又涨价20%,现在价格与原价相比(
).
A.现价高
B.原价高
C.与原价相等
D.无法比较
【课前预习】答案
1.C
2.D
3.A
4.D
5.B
1.K先生正在看《阿Q正传》,这里K、Q表示什么?
2.从A地到B地要走3个小时.这里A、B表示什么?
字母可表示:人名
3.加法交换律:
a+b=b+a
字母可表示:地名
字母可表示:运算定律
生活中的字母
导入新课
【学习探究】
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100
km/h.根据已知数据求出列车在冻土地段行驶的路程.
(1)2
h行驶多少千米?3
h呢?8
h呢?t
h呢?
(2)字母t表示时间有什么意义?
如果用v表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
怎样分析数量关系,并用含有字母的式子表示数量关系呢?
(2)绕地球飞行n周,约需90n
分钟
解:
问题1:中国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.它在椭圆形轨道上环绕地球飞过1周,约需90分钟.试求:
(1)
绕地球飞行10周约需多少分钟?
(2)绕地球飞行n周约需多少分钟?
(1)绕地球飞行10周,约需90×10=900
(分钟)
含字母的式子的书写
一
问题2:像0,±2,±4,±6,…能被2整除的数叫做偶数;像±1,
±3,±5,…不能被2整除的数叫做奇数.
如果k表示一个整数,那么偶数表示为
____
,奇数表示为
____
.
整数
…
-3
-2
-1
0
1
2
3
…
k
…
偶数
…
-6
-4
-2
0
2
4
6
…
____
…
奇数
…
-7
-5
-3
-1
1
3
5
…
____
…
2k
2k-1
2k-1
2k
问题3:如图,在月历中用长方形任意框出的3
个数
之间有怎样的关系?你会用一个等式表示
这个关系吗?
a+c=2a
或
b-a=c-b
从上述例子可以看出:用字母表示数,可以把一些数量关系抽象化,使它具有一般性.
用含有字母的式子表示下列数量
例1
(2)练习簿的单价为b
元,
a本练习簿的总价是
元.
(1)练习簿的单价为a元,100本练习簿的总价是
元.
②字母和字母相乘,乘号可以省略不写或用“
·
”
表示.
一般情况下,按26个字母的顺序从左到右来写.
100a
ab
①数和字母相乘,可省略乘号,并把数字写在字母的前面
(3)练习簿的单价为0.5元,圆珠笔的单价是3.2元,
买a本练习簿和b支笔的总价是
元.
③后面带单位的相加或相减的式子要用括号括起来
(0.5a+3.2b)
④除法运算写成分数形式,即除号改为分数线
(4)小明的家离学校s千米,小明骑车上学.若每小时行
10千米,则需
时.
⑤带分数与字母相乘时,带分数要写成假分数的形式
(5)若每斤苹果
元,则买m斤苹果需
元.
(6)姚明个子高,经测量他通常跨一步的距离1米,
若取向前为正,向后为负,那么姚明向前跨
a步为
米,向后跨a步为
米.
a
-a
6.当“1”与任何字母相乘时,“1”省略不写;
当“-1”乘以字母时,只要在那个字母前加上“-”号.
1×a=a
;
(-1)×a=-a
例2(1)一条河的水流速度是2.5
km/h,船在静水中的速度是
v
km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
分析:船在河流中行驶时,船的速度需要分两种情况讨论:
顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是
km/h,逆水行驶的速度是
km/h.
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要
z
元,用式子表示买
3个篮球、5个排球、2个足球共需要的钱数;
解:(2)买3个篮球、5个排球、2个足球共需要
元.
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2
)是
.
(4)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
解:(4)这所住宅的建筑面积(单位:m2)是
.
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳:
强调:
在含有字母的式子中如果出现乘号,通常将乘号写作“·”或省略不写.例如,100×t可以写成100
·t或100t.
归纳:
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
运算定律
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a
+
b
=
b
+
a
(a
+
b)
+c=
a
+(b
+
c)
ab
=
ba
(ab)c
=
a(bc)
(a
+
b)
c
=
ac+bc
1.用字母表示数的运算律
用字母表示运算律和公式
例3
(1)小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍,
则亮亮的速度可以表示为____米/秒.
(2)如图,
用字母表示图中阴影
部分的面积是_________
m
n
p
q
3v
一个正方形盒子的棱长为acm,用含a的式子表示:
盒子的表面积S=____________;
盒子的体积V=____________.
(1)买一个篮球需要x元,买一个排球需要y元,买一个足球需要
z
元,用式子表示买
3个篮球、5个排球、2个足球共需要的钱数。
例4
用含字母的式子表示数量关系
解:买3个篮球、5个排球、2个足球共需要
元.
1.我们现在讨论的数的范围是有理数,即数a可以是正数,也可以是负数或零,所以a不一定表示正数,-a不一定表示负数.
2.同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
注意:
(1)某种商品每袋4.8元,在一个月内的销售量是m
袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是
r,h,用式子表示圆柱体的体积.
【课后练习】
1.某服装店新开张,第一天销售服装a件,第二天比第一天多销售5件,第三天的销售量是第二天的3倍少9件,则第三天销售了( )
A.(3a+6)件
B.(3a+15)件
C.(3a+9)件
D.(3a+24)件
2.下列说法中,正确的个数有
(
)
个.
①
有理数包括整数和分数;
②
一个代数式不是单项式就是多项式;③
几个有理数相乘,若负因数的个数是偶数个,则积为正数.
④
倒数等于本身的数有1,-l;
A.1
B.2
C.3
D.4
3.下列式子符合书写要求的是( )
A.-xy?
B.a-1÷b
C.4xy
D.ab×3
4.对于代数式(a+b)?,下列描述正确的是( )
A.a与b?的平方的和B.a与b的平方和C.a与b的和的平方D.a与b的平方的和
5.一个两位数的个位上的数是a,十位上的数是b,则这个两位数表示为(
)
A.A+b
B.10a+b
C.a+10b
D.ba
6.一台电脑按原价的85%出售,每台售价为y元,则这台电脑原价为______.
7.a、b两数差的5倍,用代数式可表示为_________________.
8.某校七年级有师生参加爱心捐款活动,其中有a名教师,b名学生,若平均每名教师捐x元,每名学生捐10元,则他们一共捐款___________元.
9.观察下列算式:①3?-1?=8,②5?-3?=16,③7?-5?=24,④9?-7?=32,…,请用你发现的规律将第n个式子表示出来:______________________________.
10.甲,乙两人分别从两地同时出发,若相向而行,则a小时相遇;若同向而行,则b小时甲追上乙,那么甲的速度是乙的速度的_______.
【课后练习】答案
1.、A
2.B
3.A
4.C
5.C
【课后练习】
1.C
2.D
3.A
4.D
5.B
6.
7.5(a-b)
8.(ax+10b)
9.(2n+1)2-(2n-1)2=8n
10.
