5.3 梯形的面积(课件) 数学五年级上册-西师大版(共26张PPT)
文档属性
| 名称 | 5.3 梯形的面积(课件) 数学五年级上册-西师大版(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 07:42:44 | ||
图片预览






文档简介
(共26张PPT)
梯形的面积
平行四边形的面积计算公式是怎样的?
三角形的面积计算公式是怎样的?
这些面积公式是怎样转化推导出来的?
平行四边形的面积=底×高
三角形行的面积=底×高÷2
转化成学习过的图形
自主尝试
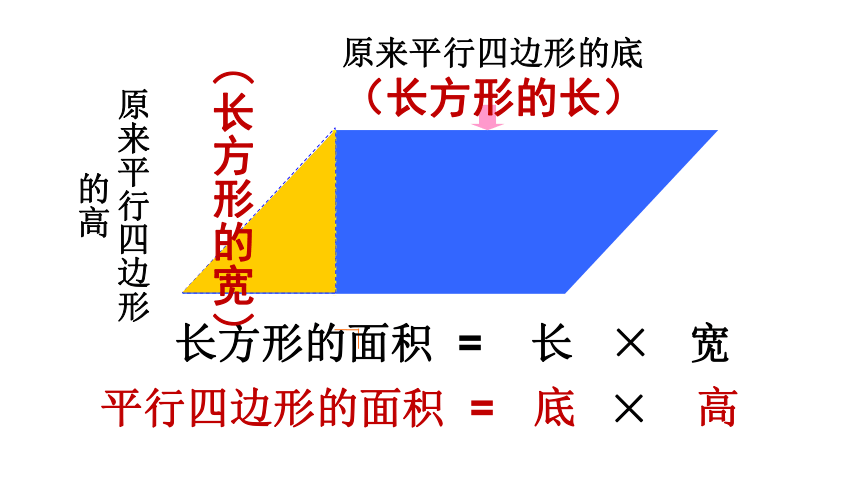
原来平行四边形的底
原来平行四边形的高
(长方形的长)
长方形的面积
=
长
×
宽
平行四边形的面积
=
×
底
高
(长方形的宽)
底
高
底
高
底
高
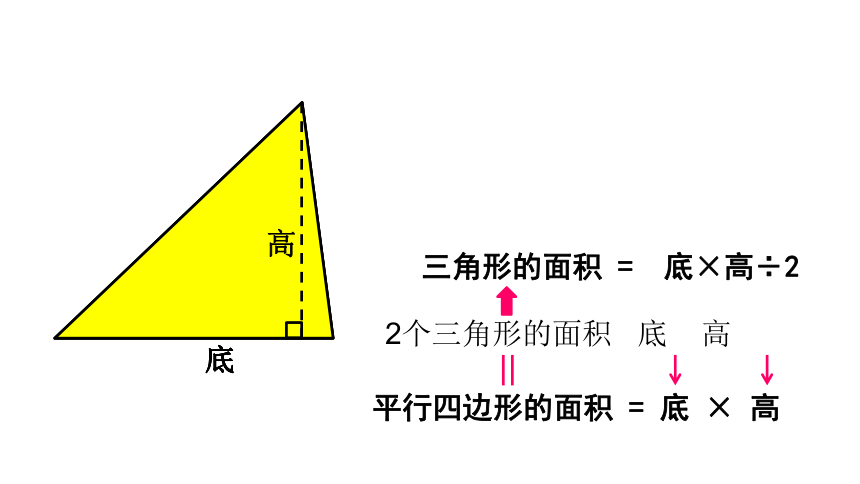
平行四边形的面积
=
底
×
高
2个三角形的面积
底
高
三角形的面积
=
底×高÷2
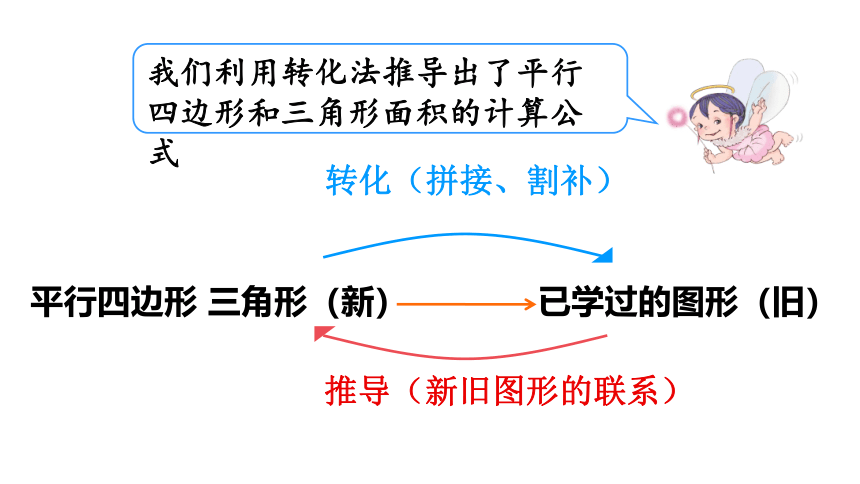
平行四边形
三角形(新)
已学过的图形(旧)
转化(拼接、割补)
推导(新旧图形的联系)
我们利用转化法推导出了平行四边形和三角形面积的计算公式
情景导入
李叔叔新买一辆车,想知道车窗玻璃有多大,你能帮他吗?
车窗玻璃是什么的形状?求车窗玻璃有多大是求什么的?
3.在探索学习的过程中,培养学生的实践能力,探索能力,使学生体验学习数学的乐趣。
1.理解和掌握梯形的面积计算公式,能正确地计算梯形的面积。
2.能够运用梯形的面积计算公式解决实际问题。
学习目标
只有一组对边平行的四边形叫梯形
两腰相等的梯形叫等腰梯形
有一个角是直角的梯形叫直角梯形
梯形有什么特征
想一想
你能猜想一下梯形的面积跟什么有关吗?
我们怎样计算梯形的面积呢?
我们动手操作,试试吧。
1.以小组为单位,利用手中的学具,根据你们的学习经验,来验证你的猜想,试着根据“转化-找联系-推导公式”的思路来探讨梯形的面积的计算方法。
2.记录你们的学习过程,做好分享交流的准备。
合作探究
以小组为单位,利用手中的学具,来展示你们的学习成果,小组成员可以相互补充。组与组之间可以相互质疑。
分享交流
平行四边形的面积
=
底
×
高
2个梯形的面积(上底+下底)
高
梯形的面积=(上底+下底)×高÷2
上底
高
下底
上底
高
下底
预设一:
上底
高
下底
上底
高
下底
预设二:
长边形的面积
=
底
×
高
2个梯形的面积(上底+下底)
高
梯形的面积=(上底+下底)×高÷2
高
下底
上底
只要是两个完全一样的梯形,我们都能把它们拼成一个平行四边形或长方形。
梯形的面积=______________________
你发现了什么?
(上底+下底)×高÷2
预设一:
梯形的面积
=
小三角形的面积
+
大三角形的面积
=
上底×高÷2
+
下底×高÷2
上底
高
下底
=(上底+下底)×高÷2
梯形的面积
=
平行四边形的面积
+
三角形的面积
=
上底×高
+(下底
-
上底)×高÷2
=(上底
+
下底)×高÷2
上底
高
下底
预设二:
预设三:
平行四边形的面积
=
底
×
高
梯形的面积
(上底+下底)÷2
高
梯形的面积=(上底+下底)×高÷2
上底
下底
高
把一个梯形剪成两个梯形
只要是运用相应的方法把梯形分割或割补成学过的图形,然后找到相应的新旧图形的联系,就能得出:
梯形的面积
=(上底
+下底)×高÷2。
你发现了什么?
S=(a+b)h÷2
梯形的面积
=(上底+下底)×高÷2
梯形上底+梯形下底
高
归纳提炼
练习反馈
夯实基础--综合应用--拓展提升
×
(2)两个面积一样的梯形定能拼成一个长方形。(
)
(1)只有一组对边平行的四边形叫做梯形。(
)
(3)上底和高分别相等的梯形面积一定相等。
(
)
√
1、判断。(对的打
“√”,错的打“×”)
×
基础巩固
×
(4)任意一个平行四边形都可以分成两个大小和形
状都一样的梯形。(
)
√
(5)梯形的面积总是平行四边形面积的一半。(
)
×
2.李叔叔的汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
S
=(a
+
b)h÷2
=(40
+
71)×40÷2
=
111×40÷2
=
2220(cm2)
S
=(a
+
b)h÷2
=(45
+
65)×40÷2
=
110×40÷2
=
2200(cm2)
3.靠墙边围成一个花坛,围花坛的篱笆长46m,求这个花坛的面积。
面积:(46
-
20)×20÷2
=
260(m2)
上底+下底=
46
-
20
=
26(m)
答:这个花坛的面积是260m2。
5.已知一个梯形的面积是15cm2。它的上底是4.5cm,高是3cm,下底是多少厘米?(列方程解决)
解:设下底是
x
cm。
(4.5
+x)×3÷2
=15
x
=
5.5
答:下底是
5.5
厘米。
体会质疑
学习了本节知识你有什么体会和大家分享;还有什么疑惑?说出来我们共同解决。
梯形的面积
平行四边形的面积计算公式是怎样的?
三角形的面积计算公式是怎样的?
这些面积公式是怎样转化推导出来的?
平行四边形的面积=底×高
三角形行的面积=底×高÷2
转化成学习过的图形
自主尝试
原来平行四边形的底
原来平行四边形的高
(长方形的长)
长方形的面积
=
长
×
宽
平行四边形的面积
=
×
底
高
(长方形的宽)
底
高
底
高
底
高
平行四边形的面积
=
底
×
高
2个三角形的面积
底
高
三角形的面积
=
底×高÷2
平行四边形
三角形(新)
已学过的图形(旧)
转化(拼接、割补)
推导(新旧图形的联系)
我们利用转化法推导出了平行四边形和三角形面积的计算公式
情景导入
李叔叔新买一辆车,想知道车窗玻璃有多大,你能帮他吗?
车窗玻璃是什么的形状?求车窗玻璃有多大是求什么的?
3.在探索学习的过程中,培养学生的实践能力,探索能力,使学生体验学习数学的乐趣。
1.理解和掌握梯形的面积计算公式,能正确地计算梯形的面积。
2.能够运用梯形的面积计算公式解决实际问题。
学习目标
只有一组对边平行的四边形叫梯形
两腰相等的梯形叫等腰梯形
有一个角是直角的梯形叫直角梯形
梯形有什么特征
想一想
你能猜想一下梯形的面积跟什么有关吗?
我们怎样计算梯形的面积呢?
我们动手操作,试试吧。
1.以小组为单位,利用手中的学具,根据你们的学习经验,来验证你的猜想,试着根据“转化-找联系-推导公式”的思路来探讨梯形的面积的计算方法。
2.记录你们的学习过程,做好分享交流的准备。
合作探究
以小组为单位,利用手中的学具,来展示你们的学习成果,小组成员可以相互补充。组与组之间可以相互质疑。
分享交流
平行四边形的面积
=
底
×
高
2个梯形的面积(上底+下底)
高
梯形的面积=(上底+下底)×高÷2
上底
高
下底
上底
高
下底
预设一:
上底
高
下底
上底
高
下底
预设二:
长边形的面积
=
底
×
高
2个梯形的面积(上底+下底)
高
梯形的面积=(上底+下底)×高÷2
高
下底
上底
只要是两个完全一样的梯形,我们都能把它们拼成一个平行四边形或长方形。
梯形的面积=______________________
你发现了什么?
(上底+下底)×高÷2
预设一:
梯形的面积
=
小三角形的面积
+
大三角形的面积
=
上底×高÷2
+
下底×高÷2
上底
高
下底
=(上底+下底)×高÷2
梯形的面积
=
平行四边形的面积
+
三角形的面积
=
上底×高
+(下底
-
上底)×高÷2
=(上底
+
下底)×高÷2
上底
高
下底
预设二:
预设三:
平行四边形的面积
=
底
×
高
梯形的面积
(上底+下底)÷2
高
梯形的面积=(上底+下底)×高÷2
上底
下底
高
把一个梯形剪成两个梯形
只要是运用相应的方法把梯形分割或割补成学过的图形,然后找到相应的新旧图形的联系,就能得出:
梯形的面积
=(上底
+下底)×高÷2。
你发现了什么?
S=(a+b)h÷2
梯形的面积
=(上底+下底)×高÷2
梯形上底+梯形下底
高
归纳提炼
练习反馈
夯实基础--综合应用--拓展提升
×
(2)两个面积一样的梯形定能拼成一个长方形。(
)
(1)只有一组对边平行的四边形叫做梯形。(
)
(3)上底和高分别相等的梯形面积一定相等。
(
)
√
1、判断。(对的打
“√”,错的打“×”)
×
基础巩固
×
(4)任意一个平行四边形都可以分成两个大小和形
状都一样的梯形。(
)
√
(5)梯形的面积总是平行四边形面积的一半。(
)
×
2.李叔叔的汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
S
=(a
+
b)h÷2
=(40
+
71)×40÷2
=
111×40÷2
=
2220(cm2)
S
=(a
+
b)h÷2
=(45
+
65)×40÷2
=
110×40÷2
=
2200(cm2)
3.靠墙边围成一个花坛,围花坛的篱笆长46m,求这个花坛的面积。
面积:(46
-
20)×20÷2
=
260(m2)
上底+下底=
46
-
20
=
26(m)
答:这个花坛的面积是260m2。
5.已知一个梯形的面积是15cm2。它的上底是4.5cm,高是3cm,下底是多少厘米?(列方程解决)
解:设下底是
x
cm。
(4.5
+x)×3÷2
=15
x
=
5.5
答:下底是
5.5
厘米。
体会质疑
学习了本节知识你有什么体会和大家分享;还有什么疑惑?说出来我们共同解决。
