5.6 问题解决(课件) 数学五年级上册-西师大版(共19张PPT)
文档属性
| 名称 | 5.6 问题解决(课件) 数学五年级上册-西师大版(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 920.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
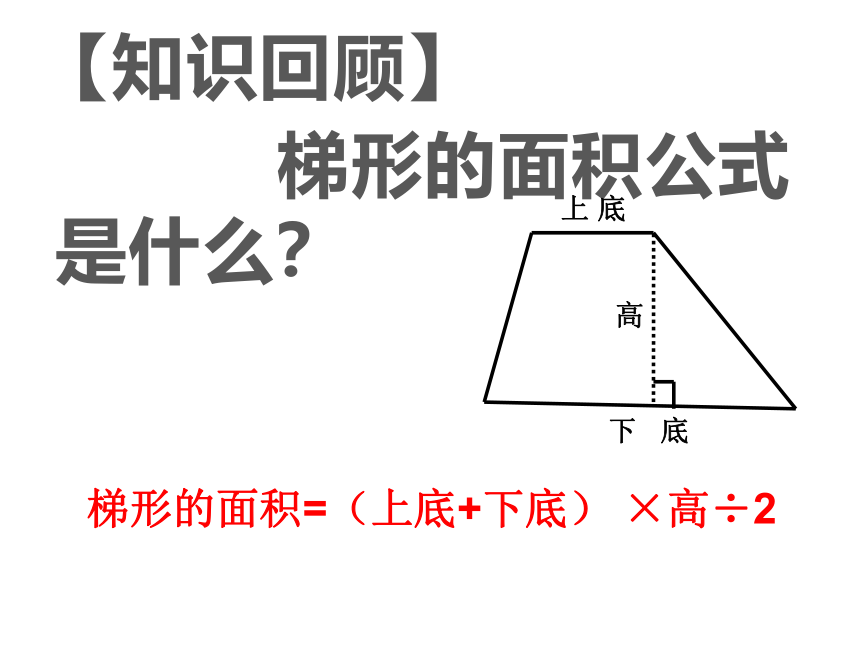
【知识回顾】
梯形的面积公式是什么?
上
底
下
底
高
梯形的面积=(上底+下底)
×高÷2
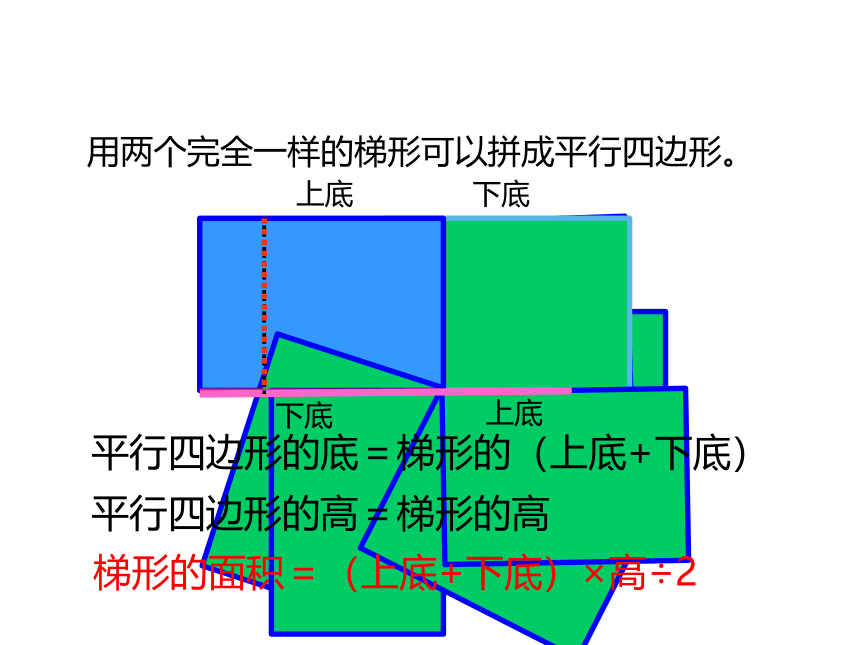
上节课我们是怎样研究出梯形面积的计算方法?
回顾
上底
下底
下底
上底
平行四边形的底=梯形的(上底+下底)
平行四边形的高=梯形的高
梯形的面积=(上底+下底)×高÷2
用两个完全一样的梯形可以拼成平行四边形。
例1、有一堆圆木,摆成下图形状,该怎样计算圆木的根数?
从上往下,一层
比一层多放1根。
从下往上,一层
比一层少放1根。
例1、有一堆圆木,摆成下图形状,该怎样计算圆木的根数?
以小组为单位先讨论以下问题并由小组长负责记录,再派代表向全班汇报:
(1)这堆原木一共有多少根?你想到了几种计算方法?
例1、有一堆圆木,摆成下图形状,该怎样计算圆木的根数?
方法一:一层一层地加。
3+4+5+6+7+8
=33(根)
方法二:利用数据规律组合相加(上下分组向中间加)
(3+8)+(4+7)+(5+6)
=11×3
=33(根)。
(3+8)×6÷2=33(根)
方法三:
画一画
(3+8)×6÷2=33(根)
总根数=(顶层根数+底层根数)×层数÷2
像这样堆放的原木、钢管等,通常可以用下面的算法求总根数:
总根数=(顶层根数+底层根数)
×层数÷2
梯形面积=(上底
+
下底)
×
高
÷2
这个公式与梯形的面积公式是怎样对应的?
(顶层根数+底层根数)
×层数÷2
(4+20)
×17÷2
=24
×17÷2
=408÷2
=204(支)
答:一共有204支铅笔。
(顶层根数+底层根数)
×层数÷2
(1+8)
×6÷2
=27(根)
检验:33-2=31(根)
×
为什么这时不能用这个公式?
注意:必须是有规律的依次增加
(或减少)相同的数量,才能用这个公式。
2、云龙小学合唱队庆祝元旦表演时排列队形成一个梯形,第一行4人,以后每一行都比前一行多4人,最后一行有24人,一共排了6行,这个合唱队一共有多少人?
总根数=(顶层根数+底层根数)
×
层数÷2
总人数=(第一行人数+最后一行人数)×行数÷2
(
4
+
24)×6÷2
=84(人)
答:这个合唱队一共有40人。
(顶层根数+底层根数)
×层数÷2
(1+8)
×8÷2
=36(根)
检验:33+3=36(根)
为什么这时也能用这个公式?
注意:必须是有规律的依次增加
(或减少)相同的数量,才能用这个公式。
你能运用所学
知识快速算出
硬币一共有
多少枚?
…
…
…
…
…
…
100个
(1+100)
×
100
÷2
=10100
÷
2
=5050
计算:1+2+3+…+98+99+100=?
生活中有许多用到梯形法则的地方。
如:①把木棒堆成横截面是近似于梯形的形状,可用:(顶层根数+底层根数)×层数÷2=总根数这个公式来算总根数
。
②把合唱团的学生排成梯形形状的,可用:
(第一排人数+最后一排人数)×排数÷2=总人数这个公式来算总人数。
你有什么收获?
注意:必须是有规律的依次增加
(或减少)相同的数量,才能用上面公式。
Thank
you
【知识回顾】
梯形的面积公式是什么?
上
底
下
底
高
梯形的面积=(上底+下底)
×高÷2
上节课我们是怎样研究出梯形面积的计算方法?
回顾
上底
下底
下底
上底
平行四边形的底=梯形的(上底+下底)
平行四边形的高=梯形的高
梯形的面积=(上底+下底)×高÷2
用两个完全一样的梯形可以拼成平行四边形。
例1、有一堆圆木,摆成下图形状,该怎样计算圆木的根数?
从上往下,一层
比一层多放1根。
从下往上,一层
比一层少放1根。
例1、有一堆圆木,摆成下图形状,该怎样计算圆木的根数?
以小组为单位先讨论以下问题并由小组长负责记录,再派代表向全班汇报:
(1)这堆原木一共有多少根?你想到了几种计算方法?
例1、有一堆圆木,摆成下图形状,该怎样计算圆木的根数?
方法一:一层一层地加。
3+4+5+6+7+8
=33(根)
方法二:利用数据规律组合相加(上下分组向中间加)
(3+8)+(4+7)+(5+6)
=11×3
=33(根)。
(3+8)×6÷2=33(根)
方法三:
画一画
(3+8)×6÷2=33(根)
总根数=(顶层根数+底层根数)×层数÷2
像这样堆放的原木、钢管等,通常可以用下面的算法求总根数:
总根数=(顶层根数+底层根数)
×层数÷2
梯形面积=(上底
+
下底)
×
高
÷2
这个公式与梯形的面积公式是怎样对应的?
(顶层根数+底层根数)
×层数÷2
(4+20)
×17÷2
=24
×17÷2
=408÷2
=204(支)
答:一共有204支铅笔。
(顶层根数+底层根数)
×层数÷2
(1+8)
×6÷2
=27(根)
检验:33-2=31(根)
×
为什么这时不能用这个公式?
注意:必须是有规律的依次增加
(或减少)相同的数量,才能用这个公式。
2、云龙小学合唱队庆祝元旦表演时排列队形成一个梯形,第一行4人,以后每一行都比前一行多4人,最后一行有24人,一共排了6行,这个合唱队一共有多少人?
总根数=(顶层根数+底层根数)
×
层数÷2
总人数=(第一行人数+最后一行人数)×行数÷2
(
4
+
24)×6÷2
=84(人)
答:这个合唱队一共有40人。
(顶层根数+底层根数)
×层数÷2
(1+8)
×8÷2
=36(根)
检验:33+3=36(根)
为什么这时也能用这个公式?
注意:必须是有规律的依次增加
(或减少)相同的数量,才能用这个公式。
你能运用所学
知识快速算出
硬币一共有
多少枚?
…
…
…
…
…
…
100个
(1+100)
×
100
÷2
=10100
÷
2
=5050
计算:1+2+3+…+98+99+100=?
生活中有许多用到梯形法则的地方。
如:①把木棒堆成横截面是近似于梯形的形状,可用:(顶层根数+底层根数)×层数÷2=总根数这个公式来算总根数
。
②把合唱团的学生排成梯形形状的,可用:
(第一排人数+最后一排人数)×排数÷2=总人数这个公式来算总人数。
你有什么收获?
注意:必须是有规律的依次增加
(或减少)相同的数量,才能用上面公式。
Thank
you
