2021-2022学年高一上学期数学人教A版(2019)必修第一册3.1.1 函数的概念(第2课时)课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册3.1.1 函数的概念(第2课时)课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-16 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
(第二课时)
3.1.1函数的概念
知识回顾:
由上节课的学习我们知道,
函数的三要素为定义域、对应关系和值域,
定义域和值域都是非空数集.
在数学中有没有刻画非空数集的简单方式呢?
问题:
(1)什么叫闭区间?什么叫开区间?
什么叫半开半闭区间?
(2)区间的端点应满足什么条件?
(3)请用区间表示实数集R。
书写带有“+∞”、“-∞”的区间时,应使用
小括号还是中括号?
设a,b是两个实数,而且a<b.我们规定:
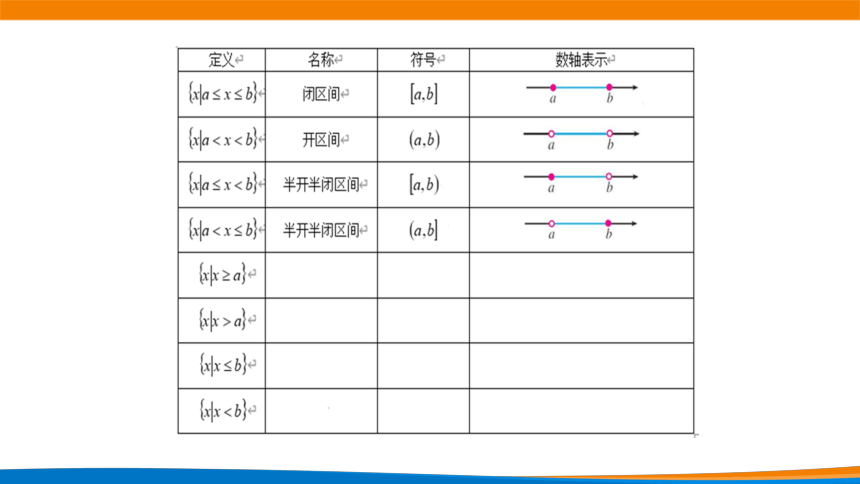
区间的概念
⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为_______.
⒉满足不等式a<x<b的实数x的集合叫做开区间,表示为_______.
⒊满足不等式a≤x<b或a<x≤b的实数x的集合叫做半开半闭区间,分别表示为_________________,
这里的_________都叫做相应区间的端点.
[a,b]
(a,b)
[a,b),(a,b]
实数a与b
实数集R可以用区间表示为
读作“无穷大”
,
我们可以把满足
的实数x的集合分别表示为
读作“负无穷大”,
∞
读作“正无穷大”,
(-∞,+∞),
思考:区间可以表示数集,数集一定可以用区间表示吗?
提示:区间可以表示数集,但只能表示一些连续的实数集的子集,一些孤立的数集不一定可以用区间表示,如集合{1,2,3}不能用区间表示.
把下列数集用区间表示:
(1){x|x≥-2}.
(2){x|x<0}.
(3){x|-1<x<1或2≤x<6}.
解析:(1){x|x≥-2}用区间表示为[-2,+∞).
(2){x|x<0}用区间表示为(-∞,0).
(3){x|-1<x<1或2≤x<6}用区间表示为
(-1,1)∪[2,6).
已知函数
(1)求函数的定义域.
(2)求
的值.
(3)当a>0时,求f(a),f(a-1)的值.
1、定义域为[-3,-2)(-2,+)
2、
3、,
(3)
1、
2、定义域:[0,)(+)
函数的定义域通常由问题的实际背景确定。
如果只给出解析式,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数的集合。
①负数不能开平方(负数不能开偶次方);
②分母不能为零;
③有限个函数的四则运算得到的新函数,它的定
义域是这有限个函数定义域的交集.
思考1:下列函数中哪个与函数y=x相等(
)
A.
B.
C.
D.
B
如果两个函数定义域相同,并且对应关系完全一致,我们就称这两个函数相等(或为同一函数)
关注函数的三要素
探究:相等函数
思考2:如何判断两个函数是否为同一函数?
下列两个函数是否表示同一个函数?
(1)
(2)
(3)
是
不是,定义域不同
不是,对应关系不同
【变式练习】
回顾本节课你有什么收获?
函数
定义
核心概念
判断同一函数的方法
三要素
再会!
(第二课时)
3.1.1函数的概念
知识回顾:
由上节课的学习我们知道,
函数的三要素为定义域、对应关系和值域,
定义域和值域都是非空数集.
在数学中有没有刻画非空数集的简单方式呢?
问题:
(1)什么叫闭区间?什么叫开区间?
什么叫半开半闭区间?
(2)区间的端点应满足什么条件?
(3)请用区间表示实数集R。
书写带有“+∞”、“-∞”的区间时,应使用
小括号还是中括号?
设a,b是两个实数,而且a<b.我们规定:
区间的概念
⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为_______.
⒉满足不等式a<x<b的实数x的集合叫做开区间,表示为_______.
⒊满足不等式a≤x<b或a<x≤b的实数x的集合叫做半开半闭区间,分别表示为_________________,
这里的_________都叫做相应区间的端点.
[a,b]
(a,b)
[a,b),(a,b]
实数a与b
实数集R可以用区间表示为
读作“无穷大”
,
我们可以把满足
的实数x的集合分别表示为
读作“负无穷大”,
∞
读作“正无穷大”,
(-∞,+∞),
思考:区间可以表示数集,数集一定可以用区间表示吗?
提示:区间可以表示数集,但只能表示一些连续的实数集的子集,一些孤立的数集不一定可以用区间表示,如集合{1,2,3}不能用区间表示.
把下列数集用区间表示:
(1){x|x≥-2}.
(2){x|x<0}.
(3){x|-1<x<1或2≤x<6}.
解析:(1){x|x≥-2}用区间表示为[-2,+∞).
(2){x|x<0}用区间表示为(-∞,0).
(3){x|-1<x<1或2≤x<6}用区间表示为
(-1,1)∪[2,6).
已知函数
(1)求函数的定义域.
(2)求
的值.
(3)当a>0时,求f(a),f(a-1)的值.
1、定义域为[-3,-2)(-2,+)
2、
3、,
(3)
1、
2、定义域:[0,)(+)
函数的定义域通常由问题的实际背景确定。
如果只给出解析式,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数的集合。
①负数不能开平方(负数不能开偶次方);
②分母不能为零;
③有限个函数的四则运算得到的新函数,它的定
义域是这有限个函数定义域的交集.
思考1:下列函数中哪个与函数y=x相等(
)
A.
B.
C.
D.
B
如果两个函数定义域相同,并且对应关系完全一致,我们就称这两个函数相等(或为同一函数)
关注函数的三要素
探究:相等函数
思考2:如何判断两个函数是否为同一函数?
下列两个函数是否表示同一个函数?
(1)
(2)
(3)
是
不是,定义域不同
不是,对应关系不同
【变式练习】
回顾本节课你有什么收获?
函数
定义
核心概念
判断同一函数的方法
三要素
再会!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
