2021-2022学年人教版八年级数学上册11.2与三角形有关的角同步练习题 (word解析版)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.2与三角形有关的角同步练习题 (word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 124.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《11.2与三角形有关的角》同步练习题(附答案)
1.定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48°
B.96°
C.88°或48°
D.48°或96°或88°
2.已知△ABC中,∠A:∠B:∠C=3:4:7,则△ABC一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
3.如图,延长△ABC的边AC到点E,过点E作DE∥BC.BG平分∠ABC,EF平分∠AED交BG的反向延长找于点F.已知3∠A=4∠F,则∠A的大小为( )
A.75°
B.74°
C.72°
D.70°
4.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=48°,∠C=68°,则∠DAE的度数是( )
A.10°
B.12°
C.14°
D.16°
5.如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是( )
A.90°
B.80°
C.60°
D.40°
6.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.45°
B.65°
C.75°
D.85°
7.如图△ABC中,∠A=65°,∠B=50°,点D在BC延长线上则∠ACD的度数是( )
A.65°
B.105°
C.115°
D.125°
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若∠ADC=65°,则∠BAC的大小为( )
A.25°
B.35°
C.50°
D.70°
9.下列说法中错误的是( )
A.三角形的三个内角中,最多有一个钝角
B.三角形三个内角中,至少有两个锐角
C.直角三角形中有两个锐角互余
D.三角形中两个内角和必大于90°
10.在Rt△ABC中,∠C=90o,∠A=2∠B,则∠A=( )
A.30o
B.45o
C.60o
D.70o
11.在Rt△ABC中,∠B是直角,∠C=50°,那么∠A的度数是( )
A.30°
B.40°
C.50°
D.130°
12.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2km.据此,可求得学校与工厂之间的距离AB等于( )
A.2km
B.3km
C.2.5km
D.4km
13.如图,∠1=140°,∠2=120°,则∠3的度数为( )
A.100°
B.120°
C.140°
D.260°
14.在△ABC中,∠A:∠B:∠C=4:4:7,则∠C的度数为
°.
15.如图,在Rt△ABC中,∠B=90°,∠A=60°.将三角形沿EF翻折,使点C与边AB上的D点重合.若∠EFD=2∠AED,则∠AED的度数为
.
16.已知:如图,在△ABC,BD⊥AC,CF⊥AB,垂足分别为点D、F,线段BD、CF交于点E,若∠A=70°,则∠BEC=
.
17.已知:如图,AD是△ABC中BC边上的高,AE平分∠BAC,若∠ABC=42°,∠ACB=70°,则∠DAE=
度.
18.由三角形内角和定理得到结论:有两个角
的三角形是直角三角形.
19.对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.
(1)求∠EBC的度数;
(2)求∠A的度数.
解:(1)∵CD⊥AB(已知),
∴∠CDB=
°.
∵∠EBC=∠CDB+∠BCD(
).
∴∠EBC=
°+35°=
°(等量代换).
(2)∵∠EBC=∠A+∠ACB(
),
∴∠A=∠EBC﹣∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=
﹣90°=
°(等量代换).
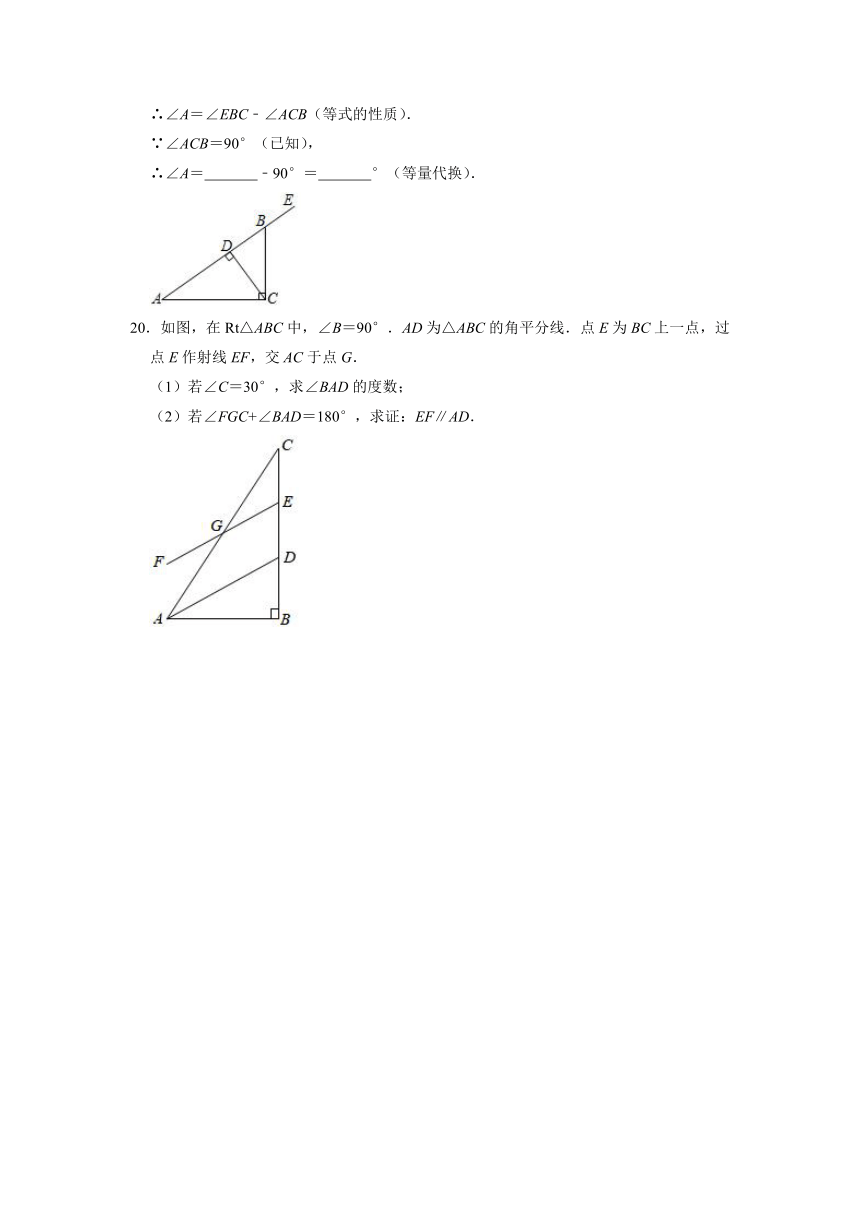
20.如图,在Rt△ABC中,∠B=90°.AD为△ABC的角平分线.点E为BC上一点,过点E作射线EF,交AC于点G.
(1)若∠C=30°,求∠BAD的度数;
(2)若∠FGC+∠BAD=180°,求证:EF∥AD.
参考答案
1.解:设三角形的三个内角分别是∠1、∠2、α且α=2∠1.
当α=48°,则∠1=24°.
当∠1=48°,则α=2∠1=96°.
当∠2=48°,则∠1+α=180°﹣∠2=132°.
∴3∠1=132°.
∴∠1=44°.
∴α=2∠1=88°.
综上:“特征角”α可能为48°或96°或88°.
故选:D.
2.解:由题意可设∠A=3x,∠B=4x,∠C=7x.
∵∠A+∠B+∠C=180°,
∴3x+4x+7x=180°.
∴x=()°.
∴7x=90°.
∴△ABC是直角三角形.
故选:B.
3.解:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DE∥BC,
∴∠ACB=∠AED,
∵BG平分∠ABC,EF平分∠AED,
∴∠ABG=∠ABC,∠AEF=∠AED,
∴∠AEF=∠AED=∠ACB,
∵∠AGF是△EFG的一个外角,
∴∠AGB=∠F+∠AEF
=∠F+∠ACB,
在△ABG中,∠A+∠ABG+∠AGB=180°,
∴∠A+∠ABC+∠F+∠ACB=180°,
∠A+∠F+(∠ABC+∠ACB)=180°,
∠A+∠F+(180°﹣∠A)=180°,
整理得:∠A+∠F=90°,
∵3∠A=4∠F,
∴∠F=∠A,
∴∠A+∠A=90°,
解得:∠A=72°.
故选:C.
4.解:∵∠B=48°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=64°,
∵AE平分∠BAC,
∴∠EAC=BAC=32°,
∵AD是△ABC的BC边上的高,
∴∠ADC=90°,
∵∠C=68°,
∴∠DAC=90°﹣∠C=22°,
∴∠DAE=∠EAC﹣∠DAC=32°﹣22°=10°,
故选:A.
5.解:由三角形的外角性质得,∠C=∠CBD﹣∠A=120°﹣40°=80°.
故选:B.
6.解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故选:C.
7.解:∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=65°+50°=115°.
故选:C.
8.解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=∠BAC,
∵∠ADC是△ABD的外角,∠ADC=65°,
∴∠B+∠BAC=65°,
∵∠C=90°,
∴∠B+∠BAC=90°,
∴∴∠BAC=50°,
故选:C.
9.解:A、三角形的三个内角中,最多有一个钝角,正确.
B、三角形三个内角中,至少有两个锐角,正确.
C、直角三角形中有两个锐角互余,正确,
D、三角形中两个内角和必大于90°,错误,比如钝角三角形的两个锐角的和小于90°.
故选:D.
10.解:∵∠C=90o,
∴∠A+∠B=90°,
∵∠A=2∠B,
∴2∠B+∠B=90°,
∴∠B=30°,
∴∠A=2∠B=60°,
故选:C.
11.解:在Rt△ABC中,∠B是直角,
∴∠A+∠C=90°,
∵∠C=50°,
∴∠A=90°﹣50°=40°,
故选:B.
12.解:∵∠A=60°,∠C=90°,AC=2km,
∴∠B=30°,
∴AB=2AC=4(km).
故选:D.
13.解:∵∠1、∠2、∠3是三角形的三个外角,
∴∠1+∠2+∠3=360°,
∵∠1=140°,∠2=120°,
∴∠3=360°﹣∠1﹣∠2=360°﹣140°﹣120°=100°,
故选:A.
14.解:在△ABC中,∠A:∠B:∠C=4:4:7,
∴设∠A=4x,∠B=4x,∠C=7x,
∵∠A+∠B+∠C=180°,
∴4x+4x+7x=180°,
解得:x=12°,
∴∠C=7×12°=84°.
故答案为:84.
15.解:设∠EFD=2∠AED=2x.
由折叠性质可知,∠EDF=∠C=90°﹣∠A=90°﹣60°=30°,
∠DEF=∠CEF,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣30°﹣2x=150°﹣2x,
∴∠CEF=150°﹣2x,
∵∠DEF+∠CEF+∠AED=180°,
∴150°﹣2x+150°﹣2x+x=180°,
解得x=40°,
即∠AED=40°.
故答案为:40°.
16.解:解法一∵BD⊥AC,CF⊥AB,
∴∠AFC=∠ADB=90°,
∵四边形内角和为360o,∠A=70°,
∴∠BEC=∠DEF=360°﹣∠AFC﹣∠ADB﹣∠A=360o﹣90o﹣90o﹣70°=110°,
故答案为:110°.
解法二:∵BD⊥AC,CF⊥AB,
∴∠BFC=∠ADB=90°,
∵∠A=70°,
∴∠ABD=90°﹣70°=20°,
∴∠BEC=∠ABD+∠BFC=110°,
故答案为:110°.
17.解:∵∠ABC=42°,∠ACB=70°,
∴∠BAC=68°.
∵AD是△ABC中BC边上的高,
∴∠ADC=90°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=34°.
∵∠AEC=∠B+∠BAE=42°+34°=76°,
∠ADC=∠EAD+∠AEC,
∴∠EAD=90°﹣∠AEC=90°﹣76°=14°.
故答案为:14.
18.解:因为三角形的内角和是180°,
若该三角形为直角三角形,则有一个角是90°,
那么剩下的两个角的和为90°.
所以另两个角互余或者和为90°..
故答案为:互余或者和为90°.
19.解:(1)∵CD⊥AB(已知),
∴∠CDB=90°.
∵∠EBC=∠CDB+∠BCD(三角形的一个外角等于与它不相邻的两个内角和).
∴∠EBC=90°+35°=125°(等量代换).
(2)∵∠EBC=∠A+∠ACB(三角形的一个外角等于与它不相邻的两个内角和),
∴∠A=∠EBC﹣∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=125°﹣90°=35°(等量代换).
故答案为(1)90;三角形的一个外角等于与它不相邻的两个内角和;90;125;
(2)三角形的一个外角等于与它不相邻的两个内角和;125°;35.
20.解:(1)在Rt△ABC中,∠B=90°,∠C=30°,
∴∠CAB=60°,
∵AD为△ABC的角平分线,
∴∠BAD=∠CAB=30°;
(2)证明:∵AD为△ABC的角平分线,
∴∠CAD=∠BAD,
∵∠FGC+∠BAD=180°,∠FGC=∠AGE,
∴∠AGE+∠CAD=180°,
∴EF∥AD
1.定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48°
B.96°
C.88°或48°
D.48°或96°或88°
2.已知△ABC中,∠A:∠B:∠C=3:4:7,则△ABC一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
3.如图,延长△ABC的边AC到点E,过点E作DE∥BC.BG平分∠ABC,EF平分∠AED交BG的反向延长找于点F.已知3∠A=4∠F,则∠A的大小为( )
A.75°
B.74°
C.72°
D.70°
4.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=48°,∠C=68°,则∠DAE的度数是( )
A.10°
B.12°
C.14°
D.16°
5.如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是( )
A.90°
B.80°
C.60°
D.40°
6.将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.45°
B.65°
C.75°
D.85°
7.如图△ABC中,∠A=65°,∠B=50°,点D在BC延长线上则∠ACD的度数是( )
A.65°
B.105°
C.115°
D.125°
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若∠ADC=65°,则∠BAC的大小为( )
A.25°
B.35°
C.50°
D.70°
9.下列说法中错误的是( )
A.三角形的三个内角中,最多有一个钝角
B.三角形三个内角中,至少有两个锐角
C.直角三角形中有两个锐角互余
D.三角形中两个内角和必大于90°
10.在Rt△ABC中,∠C=90o,∠A=2∠B,则∠A=( )
A.30o
B.45o
C.60o
D.70o
11.在Rt△ABC中,∠B是直角,∠C=50°,那么∠A的度数是( )
A.30°
B.40°
C.50°
D.130°
12.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2km.据此,可求得学校与工厂之间的距离AB等于( )
A.2km
B.3km
C.2.5km
D.4km
13.如图,∠1=140°,∠2=120°,则∠3的度数为( )
A.100°
B.120°
C.140°
D.260°
14.在△ABC中,∠A:∠B:∠C=4:4:7,则∠C的度数为
°.
15.如图,在Rt△ABC中,∠B=90°,∠A=60°.将三角形沿EF翻折,使点C与边AB上的D点重合.若∠EFD=2∠AED,则∠AED的度数为
.
16.已知:如图,在△ABC,BD⊥AC,CF⊥AB,垂足分别为点D、F,线段BD、CF交于点E,若∠A=70°,则∠BEC=
.
17.已知:如图,AD是△ABC中BC边上的高,AE平分∠BAC,若∠ABC=42°,∠ACB=70°,则∠DAE=
度.
18.由三角形内角和定理得到结论:有两个角
的三角形是直角三角形.
19.对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.
(1)求∠EBC的度数;
(2)求∠A的度数.
解:(1)∵CD⊥AB(已知),
∴∠CDB=
°.
∵∠EBC=∠CDB+∠BCD(
).
∴∠EBC=
°+35°=
°(等量代换).
(2)∵∠EBC=∠A+∠ACB(
),
∴∠A=∠EBC﹣∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=
﹣90°=
°(等量代换).
20.如图,在Rt△ABC中,∠B=90°.AD为△ABC的角平分线.点E为BC上一点,过点E作射线EF,交AC于点G.
(1)若∠C=30°,求∠BAD的度数;
(2)若∠FGC+∠BAD=180°,求证:EF∥AD.
参考答案
1.解:设三角形的三个内角分别是∠1、∠2、α且α=2∠1.
当α=48°,则∠1=24°.
当∠1=48°,则α=2∠1=96°.
当∠2=48°,则∠1+α=180°﹣∠2=132°.
∴3∠1=132°.
∴∠1=44°.
∴α=2∠1=88°.
综上:“特征角”α可能为48°或96°或88°.
故选:D.
2.解:由题意可设∠A=3x,∠B=4x,∠C=7x.
∵∠A+∠B+∠C=180°,
∴3x+4x+7x=180°.
∴x=()°.
∴7x=90°.
∴△ABC是直角三角形.
故选:B.
3.解:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DE∥BC,
∴∠ACB=∠AED,
∵BG平分∠ABC,EF平分∠AED,
∴∠ABG=∠ABC,∠AEF=∠AED,
∴∠AEF=∠AED=∠ACB,
∵∠AGF是△EFG的一个外角,
∴∠AGB=∠F+∠AEF
=∠F+∠ACB,
在△ABG中,∠A+∠ABG+∠AGB=180°,
∴∠A+∠ABC+∠F+∠ACB=180°,
∠A+∠F+(∠ABC+∠ACB)=180°,
∠A+∠F+(180°﹣∠A)=180°,
整理得:∠A+∠F=90°,
∵3∠A=4∠F,
∴∠F=∠A,
∴∠A+∠A=90°,
解得:∠A=72°.
故选:C.
4.解:∵∠B=48°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=64°,
∵AE平分∠BAC,
∴∠EAC=BAC=32°,
∵AD是△ABC的BC边上的高,
∴∠ADC=90°,
∵∠C=68°,
∴∠DAC=90°﹣∠C=22°,
∴∠DAE=∠EAC﹣∠DAC=32°﹣22°=10°,
故选:A.
5.解:由三角形的外角性质得,∠C=∠CBD﹣∠A=120°﹣40°=80°.
故选:B.
6.解:∵∠2+60°+45°=180°,
∴∠2=75°.
∵直尺的上下两边平行,
∴∠1=∠2=75°.
故选:C.
7.解:∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠B=65°+50°=115°.
故选:C.
8.解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=∠BAC,
∵∠ADC是△ABD的外角,∠ADC=65°,
∴∠B+∠BAC=65°,
∵∠C=90°,
∴∠B+∠BAC=90°,
∴∴∠BAC=50°,
故选:C.
9.解:A、三角形的三个内角中,最多有一个钝角,正确.
B、三角形三个内角中,至少有两个锐角,正确.
C、直角三角形中有两个锐角互余,正确,
D、三角形中两个内角和必大于90°,错误,比如钝角三角形的两个锐角的和小于90°.
故选:D.
10.解:∵∠C=90o,
∴∠A+∠B=90°,
∵∠A=2∠B,
∴2∠B+∠B=90°,
∴∠B=30°,
∴∠A=2∠B=60°,
故选:C.
11.解:在Rt△ABC中,∠B是直角,
∴∠A+∠C=90°,
∵∠C=50°,
∴∠A=90°﹣50°=40°,
故选:B.
12.解:∵∠A=60°,∠C=90°,AC=2km,
∴∠B=30°,
∴AB=2AC=4(km).
故选:D.
13.解:∵∠1、∠2、∠3是三角形的三个外角,
∴∠1+∠2+∠3=360°,
∵∠1=140°,∠2=120°,
∴∠3=360°﹣∠1﹣∠2=360°﹣140°﹣120°=100°,
故选:A.
14.解:在△ABC中,∠A:∠B:∠C=4:4:7,
∴设∠A=4x,∠B=4x,∠C=7x,
∵∠A+∠B+∠C=180°,
∴4x+4x+7x=180°,
解得:x=12°,
∴∠C=7×12°=84°.
故答案为:84.
15.解:设∠EFD=2∠AED=2x.
由折叠性质可知,∠EDF=∠C=90°﹣∠A=90°﹣60°=30°,
∠DEF=∠CEF,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣30°﹣2x=150°﹣2x,
∴∠CEF=150°﹣2x,
∵∠DEF+∠CEF+∠AED=180°,
∴150°﹣2x+150°﹣2x+x=180°,
解得x=40°,
即∠AED=40°.
故答案为:40°.
16.解:解法一∵BD⊥AC,CF⊥AB,
∴∠AFC=∠ADB=90°,
∵四边形内角和为360o,∠A=70°,
∴∠BEC=∠DEF=360°﹣∠AFC﹣∠ADB﹣∠A=360o﹣90o﹣90o﹣70°=110°,
故答案为:110°.
解法二:∵BD⊥AC,CF⊥AB,
∴∠BFC=∠ADB=90°,
∵∠A=70°,
∴∠ABD=90°﹣70°=20°,
∴∠BEC=∠ABD+∠BFC=110°,
故答案为:110°.
17.解:∵∠ABC=42°,∠ACB=70°,
∴∠BAC=68°.
∵AD是△ABC中BC边上的高,
∴∠ADC=90°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=34°.
∵∠AEC=∠B+∠BAE=42°+34°=76°,
∠ADC=∠EAD+∠AEC,
∴∠EAD=90°﹣∠AEC=90°﹣76°=14°.
故答案为:14.
18.解:因为三角形的内角和是180°,
若该三角形为直角三角形,则有一个角是90°,
那么剩下的两个角的和为90°.
所以另两个角互余或者和为90°..
故答案为:互余或者和为90°.
19.解:(1)∵CD⊥AB(已知),
∴∠CDB=90°.
∵∠EBC=∠CDB+∠BCD(三角形的一个外角等于与它不相邻的两个内角和).
∴∠EBC=90°+35°=125°(等量代换).
(2)∵∠EBC=∠A+∠ACB(三角形的一个外角等于与它不相邻的两个内角和),
∴∠A=∠EBC﹣∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=125°﹣90°=35°(等量代换).
故答案为(1)90;三角形的一个外角等于与它不相邻的两个内角和;90;125;
(2)三角形的一个外角等于与它不相邻的两个内角和;125°;35.
20.解:(1)在Rt△ABC中,∠B=90°,∠C=30°,
∴∠CAB=60°,
∵AD为△ABC的角平分线,
∴∠BAD=∠CAB=30°;
(2)证明:∵AD为△ABC的角平分线,
∴∠CAD=∠BAD,
∵∠FGC+∠BAD=180°,∠FGC=∠AGE,
∴∠AGE+∠CAD=180°,
∴EF∥AD
