4.7 相似三角形的性质同步练习2021-2022学年九年级数学北师大版上册(Word版 含答案)
文档属性
| 名称 | 4.7 相似三角形的性质同步练习2021-2022学年九年级数学北师大版上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 231.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 13:11:46 | ||
图片预览




文档简介
4.7
相似三角形的性质
一、选择题
1.两个相似三角形△ABC与△DEF的面积比为1:4,则它们的相似比为( )
A.1:16
B.16:1
C.1:2
D.2:1
2已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
A.4:3
B.3:4
C.16:9
D.9:16
3如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( )
A.1:2
B.1:4
C.2:1
D.4:1
4两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
5已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
A.2:3
B.4:16
C.3:2
D.16:4
6两个相似三角形的面积比是9:16,则这两个三角形的相似比和周长的比分别为( )
A.9:16;3:4
B.3:4;9:16
C.9:4;9:16
D.3:4;3:4
7若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
A.1:2
B.1:
C.2:1
D.1:4
8图中的两个三角形相似,且AB=2,A′B′=1,则△A′B′C′与△ABC的相似比是( )
A.1:2
B.2:1
C.3:1
D.1:3
二、填空题
9若△ABC∽△A′B′C′,且,若△ABC的面积为27cm2,则△A′B′C′的面积为
.
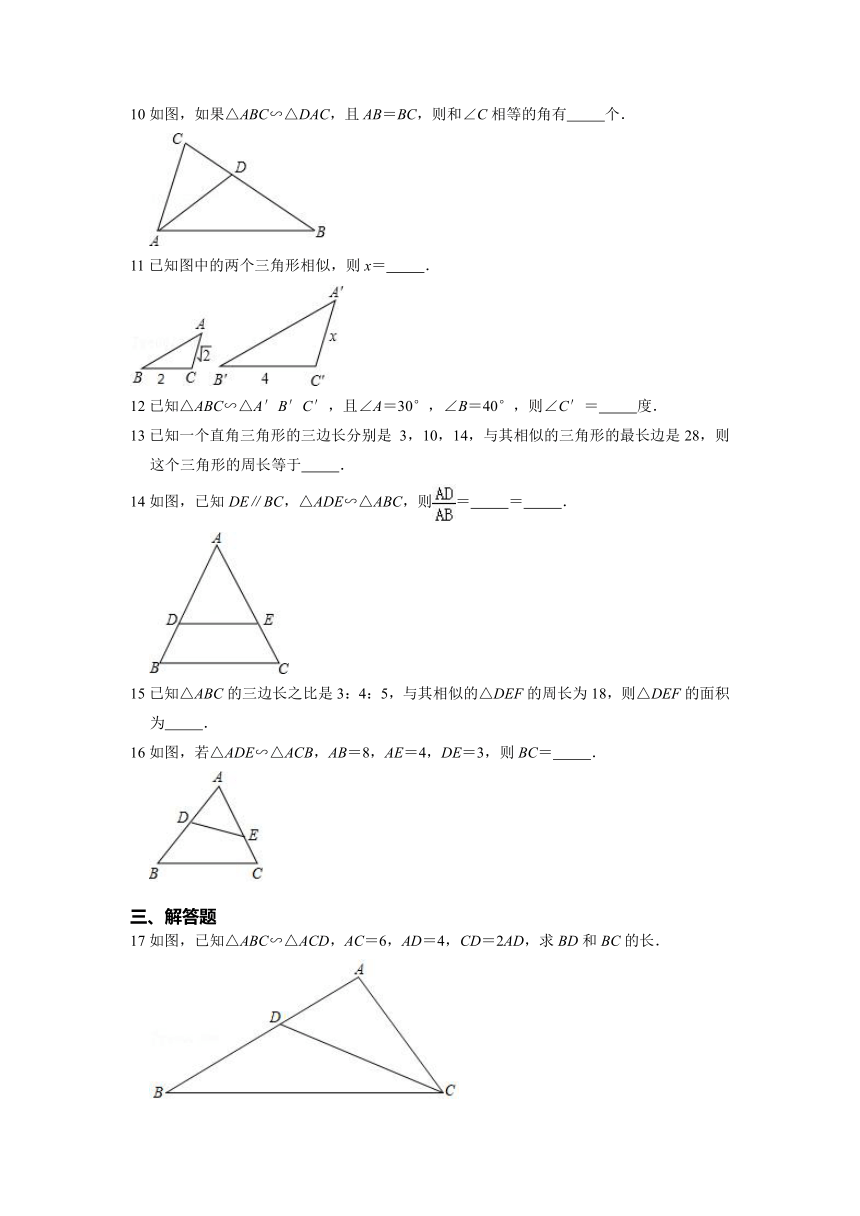
10如图,如果△ABC∽△DAC,且AB=BC,则和∠C相等的角有
个.
11已知图中的两个三角形相似,则x=
.
12已知△ABC∽△A′B′C′,且∠A=30°,∠B=40°,则∠C′=
度.
13已知一个直角三角形的三边长分别是
3,10,14,与其相似的三角形的最长边是28,则这个三角形的周长等于
.
14如图,已知DE∥BC,△ADE∽△ABC,则=
=
.
15已知△ABC的三边长之比是3:4:5,与其相似的△DEF的周长为18,则△DEF的面积为
.
16如图,若△ADE∽△ACB,AB=8,AE=4,DE=3,则BC=
.
三、解答题
17如图,已知△ABC∽△ACD,AC=6,AD=4,CD=2AD,求BD和BC的长.
18如图,△ABC与△ADB相似,AD=4,CD=6,求这两个三角形的相似比.
19如图所示,△ABC∽△ADE,试说明△ABD∽△ACE.
20如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
21如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2.
(1)DE与AB的长度之比是多少?
(2)已知直角三角形ABC的周长是12cm,面积是6cm2,求直角三角形DEF的周长与面积.
22如图所示,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
4.7
相似三角形的性质
一、选择题
1.两个相似三角形△ABC与△DEF的面积比为1:4,则它们的相似比为( )
A.1:16
B.16:1
C.1:2
D.2:1
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】利用相似三角形的面积的比等于相似比的平方,进而得出答案.
【解答】解:∵两个相似三角形△ABC与△DEF的面积比为1:4,
∴它们的相似比为:1:2.
故选:C.
2已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
A.4:3
B.3:4
C.16:9
D.9:16
【考点】相似三角形的性质.
【答案】D
【分析】已知相似三角形的相似比,根据相似三角形的面积比等于相似比的平方可直接得出答案.
【解答】解:∵△ABC∽△DEF,且相似比为3:4,
∴△DEF与△ABC的面积比为32:42,即△ABC与△DEF的面积比为9:16.
故选:D.
3如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( )
A.1:2
B.1:4
C.2:1
D.4:1
【考点】相似三角形的性质.
【答案】B
【分析】依据相似三角形面积的比等于相似比的平方,即可求解.
【解答】解:△ADE与△ABC的面积比为(1:2)2=1:4.
故选:B.
4两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据题意两个三角形的相似比是15:23,可得周长比为15:23,计算出周长相差8份及每份的长,可得两三角形周长.
【解答】解:根据题意两个三角形的相似比是15:23,周长比就是15:23,
大小周长相差8份,所以每份的周长是40÷8=5cm,
所以两个三角形的周长分别为5×15=75cm,5×23=115cm.
故选:C.
5已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
A.2:3
B.4:16
C.3:2
D.16:4
【考点】相似三角形的性质.
【答案】A
【分析】相似三角形对应边上中线的比等于相似比,根据以上性质得出即可.
【解答】解:∵△ABC∽△DEF,△ABC与△DEF的相似比为2:3,
∴△ABC与△DEF对应边上中线的比是2:3,
故选:A.
6两个相似三角形的面积比是9:16,则这两个三角形的相似比和周长的比分别为( )
A.9:16;3:4
B.3:4;9:16
C.9:4;9:16
D.3:4;3:4
【考点】相似三角形的性质.
【答案】D
【分析】根据相似三角形面积的比等于相似比的平方、相似三角形周长的比等于相似比解答即可.
【解答】解:∵两个相似三角形的面积比是9:16,
∴这两个三角形的相似比为3:4,
∴这两个三角形的周长的比为3:4,
故选:D.
7若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
A.1:2
B.1:
C.2:1
D.1:4
【考点】相似三角形的性质.
【答案】D
【分析】根据相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方解答即可.
【解答】解:∵两个相似三角形的周长之比是1:2,
∴两个相似三角形的相似比是1:2,
∴它们的面积之比是:1:4,
故选:D.
8图中的两个三角形相似,且AB=2,A′B′=1,则△A′B′C′与△ABC的相似比是( )
A.1:2
B.2:1
C.3:1
D.1:3
【考点】相似三角形的性质.
【答案】A
【分析】根据相似三角形相似比等于对应边的比解答.
【解答】解:∵AB=2,A′B′=1,
∴△A′B′C′与△ABC的相似比=A′B′:AB=1:2.
故选:A.
二、填空题
9若△ABC∽△A′B′C′,且,若△ABC的面积为27cm2,则△A′B′C′的面积为
.
【考点】相似三角形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】48cm2.
【分析】根据相似三角形的面积之比等于相似比的平方,可以直接求出结果.
【解答】解:∵△ABC∽△A′B′C′,,
∴=()2=()2=,
即=,
解得:△A′B′C′的面积=48(cm2).
故答案为:48cm2.
10如图,如果△ABC∽△DAC,且AB=BC,则和∠C相等的角有
个.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】先根据相似三角形的判定定理求出△DAC也是等腰三角形,再根据相似三角形的对应角相等即可解答.
【解答】解:∵BC=AC,∴∠CAB=∠C,
又∵△ABC∽△DAC,∴△DAC也是等腰三角形,
∴AC=AD,∠C=∠DAC,
与∠C相等的角是∠DAC以及∠CAB共两个.
11已知图中的两个三角形相似,则x=
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】根据相似三角形的性质求解即可.
【解答】解:∵△ABC∽△A′B′C′,
∴BC:B′C′=AC:A′C′,
∴2:4=:x,
∴x=2.
故答案为2.
12已知△ABC∽△A′B′C′,且∠A=30°,∠B=40°,则∠C′=
度.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】利用相似三角形的对应角相等可求∠C.
【解答】解:∵△ABC∽△A′B′C′,且∠A=30°,∠B=40°,
∴∠A′=∠A=30°,∠B′=∠B=40°,
∴∠C′=110°.
13已知一个直角三角形的三边长分别是
3,10,14,与其相似的三角形的最长边是28,则这个三角形的周长等于
.
【考点】相似三角形的性质.
【专题】计算题.
【答案】见试题解答内容
【分析】先设所求三角形的周长是x,由于两个三角形相似,利用相似三角形周长比等于相似比可得关于x的方程,解即可.
【解答】解:设所求三角形的周长是x,
∵两个三角形相似,
∴=,
解得x=54.
故答案是54.
14如图,已知DE∥BC,△ADE∽△ABC,则=
=
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】△ADE∽△ABC根据相似三角形的对应边的比相等,得到==.
【解答】解:∵△ADE∽△ABC,∴==.
15已知△ABC的三边长之比是3:4:5,与其相似的△DEF的周长为18,则△DEF的面积为
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】判断出△ABC是直角三角形,然后根据相似比和周长求出各边长,求出△DEF的面积.
【解答】解:根据勾股定理逆定理,△DEF与△ABC均为直角三角形,设△DEF三边分别为3x,4x,5x则3x+4x+5x=18,x=三边长分别为:,6,,所以S△DEF=×6×=13.5.
16如图,若△ADE∽△ACB,AB=8,AE=4,DE=3,则BC=
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】根据相似三角形的对应边的比相等列出比例式,计算即可.
【解答】解:∵△ADE∽△ACB,
∴=,即=,
解得,BC=6,
故答案为6.
三、解答题
17如图,已知△ABC∽△ACD,AC=6,AD=4,CD=2AD,求BD和BC的长.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】根据相似三角形的性质列出比例式,代入计算即可.
【解答】解:∵AD=4,CD=2AD,
∴CD=8,
∵△ABC∽△ACD,
∴==,即==,
解得,AB=9,BC=12,
∴BD=AB﹣AD=5.
18如图,△ABC与△ADB相似,AD=4,CD=6,求这两个三角形的相似比.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】先根据相似三角形对应边的比相等得出=,求出AB2=AC?AD=40,再根据相似比的定义即可求解.
【解答】解:∵△ABC与△ADB相似,
∴△ABC∽△ADB,
∴=,
∴AB2=AC?AD=10×4=40,
∴△ABC与△ADB的相似比为==.
19如图所示,△ABC∽△ADE,试说明△ABD∽△ACE.
【考点】相似三角形的判定与性质.
【专题】证明题.
【答案】见试题解答内容
【分析】由相似三角形的性质可知:,∠BAC=∠DAE,然后可证明∠BAD=∠CAE,最后依据相似三角形的判定定理进行证明即可.
【解答】证明:∵△ABC∽△ADE,
∴,∠BAC=∠DAE.
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.
∵且∠BAD=∠CAE,
∴△ABD∽△ACE.
20如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】由△ABC∽△ACD,且AD=5,BD=4,根据相似三角形的对应边成比例,可求得AC的长,继而求得答案.
【解答】解:∵AD=5,BD=4,
∴AB=AD+BD=9,
∵△ABC∽△ACD,
∴,
∴,
解得:AC=3,
∴△ACD与△ABC的相似比为:==.
21如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2.
(1)DE与AB的长度之比是多少?
(2)已知直角三角形ABC的周长是12cm,面积是6cm2,求直角三角形DEF的周长与面积.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】根据相似三角形的对应边的比等于相似比,周长比等于相似比,面积比等于相似比的平方解题即可.
【解答】解:(1)由相似变换可得:DE:AB=DF:AC=2:3;
(2)∵AC:DF=3:2,
∴△DEF的周长:△ABC的周长=2:3,
S△DEF:S△ABC=4:9,
∵直角三角形ABC的周长是12cm,面积是6cm2
∴△DEF的周长为8cm,S△DEF=cm2.
22如图所示,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
【考点】相似三角形的性质.
【专题】压轴题;分类讨论.
【答案】见试题解答内容
【分析】由∠C=90°,BC=8cm,AC:AB=3:5,利用勾股定理即可求得AB与AC的长,然后设过t秒时,以C、P、Q为顶点的三角形恰与△ABC相似,则可得BP=2tcm,CP=BC﹣BP=8﹣2t(cm),CQ=tcm,再分别从当时,△CPQ∽△CBA与当时,△CPQ∽△CAB,去分析求解即可求得答案.
【解答】解:∵∠C=90°,BC=8cm,AC:AB=3:5,
∴设AC=3xcm,AB=5xcm,
则BC==4x(cm),
即4x=8,
解得:x=2,
∴AC=6cm,AB=10cm,
∴BC=8cm,
设过t秒时,以C、P、Q为顶点的三角形恰与△ABC相似,
则BP=2tcm,CP=BC﹣BP=8﹣2t(cm),CQ=tcm,
∵∠C是公共角,
∴①当,即时,△CPQ∽△CBA,
解得:t=2.4,
②当,即时,△CPQ∽△CAB,
解得:t=,
∴过2.4或秒时,以C、P、Q为顶点的三角形恰与△ABC相似.
相似三角形的性质
一、选择题
1.两个相似三角形△ABC与△DEF的面积比为1:4,则它们的相似比为( )
A.1:16
B.16:1
C.1:2
D.2:1
2已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
A.4:3
B.3:4
C.16:9
D.9:16
3如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( )
A.1:2
B.1:4
C.2:1
D.4:1
4两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
5已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
A.2:3
B.4:16
C.3:2
D.16:4
6两个相似三角形的面积比是9:16,则这两个三角形的相似比和周长的比分别为( )
A.9:16;3:4
B.3:4;9:16
C.9:4;9:16
D.3:4;3:4
7若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
A.1:2
B.1:
C.2:1
D.1:4
8图中的两个三角形相似,且AB=2,A′B′=1,则△A′B′C′与△ABC的相似比是( )
A.1:2
B.2:1
C.3:1
D.1:3
二、填空题
9若△ABC∽△A′B′C′,且,若△ABC的面积为27cm2,则△A′B′C′的面积为
.
10如图,如果△ABC∽△DAC,且AB=BC,则和∠C相等的角有
个.
11已知图中的两个三角形相似,则x=
.
12已知△ABC∽△A′B′C′,且∠A=30°,∠B=40°,则∠C′=
度.
13已知一个直角三角形的三边长分别是
3,10,14,与其相似的三角形的最长边是28,则这个三角形的周长等于
.
14如图,已知DE∥BC,△ADE∽△ABC,则=
=
.
15已知△ABC的三边长之比是3:4:5,与其相似的△DEF的周长为18,则△DEF的面积为
.
16如图,若△ADE∽△ACB,AB=8,AE=4,DE=3,则BC=
.
三、解答题
17如图,已知△ABC∽△ACD,AC=6,AD=4,CD=2AD,求BD和BC的长.
18如图,△ABC与△ADB相似,AD=4,CD=6,求这两个三角形的相似比.
19如图所示,△ABC∽△ADE,试说明△ABD∽△ACE.
20如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
21如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2.
(1)DE与AB的长度之比是多少?
(2)已知直角三角形ABC的周长是12cm,面积是6cm2,求直角三角形DEF的周长与面积.
22如图所示,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
4.7
相似三角形的性质
一、选择题
1.两个相似三角形△ABC与△DEF的面积比为1:4,则它们的相似比为( )
A.1:16
B.16:1
C.1:2
D.2:1
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】利用相似三角形的面积的比等于相似比的平方,进而得出答案.
【解答】解:∵两个相似三角形△ABC与△DEF的面积比为1:4,
∴它们的相似比为:1:2.
故选:C.
2已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )
A.4:3
B.3:4
C.16:9
D.9:16
【考点】相似三角形的性质.
【答案】D
【分析】已知相似三角形的相似比,根据相似三角形的面积比等于相似比的平方可直接得出答案.
【解答】解:∵△ABC∽△DEF,且相似比为3:4,
∴△DEF与△ABC的面积比为32:42,即△ABC与△DEF的面积比为9:16.
故选:D.
3如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( )
A.1:2
B.1:4
C.2:1
D.4:1
【考点】相似三角形的性质.
【答案】B
【分析】依据相似三角形面积的比等于相似比的平方,即可求解.
【解答】解:△ADE与△ABC的面积比为(1:2)2=1:4.
故选:B.
4两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据题意两个三角形的相似比是15:23,可得周长比为15:23,计算出周长相差8份及每份的长,可得两三角形周长.
【解答】解:根据题意两个三角形的相似比是15:23,周长比就是15:23,
大小周长相差8份,所以每份的周长是40÷8=5cm,
所以两个三角形的周长分别为5×15=75cm,5×23=115cm.
故选:C.
5已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
A.2:3
B.4:16
C.3:2
D.16:4
【考点】相似三角形的性质.
【答案】A
【分析】相似三角形对应边上中线的比等于相似比,根据以上性质得出即可.
【解答】解:∵△ABC∽△DEF,△ABC与△DEF的相似比为2:3,
∴△ABC与△DEF对应边上中线的比是2:3,
故选:A.
6两个相似三角形的面积比是9:16,则这两个三角形的相似比和周长的比分别为( )
A.9:16;3:4
B.3:4;9:16
C.9:4;9:16
D.3:4;3:4
【考点】相似三角形的性质.
【答案】D
【分析】根据相似三角形面积的比等于相似比的平方、相似三角形周长的比等于相似比解答即可.
【解答】解:∵两个相似三角形的面积比是9:16,
∴这两个三角形的相似比为3:4,
∴这两个三角形的周长的比为3:4,
故选:D.
7若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
A.1:2
B.1:
C.2:1
D.1:4
【考点】相似三角形的性质.
【答案】D
【分析】根据相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方解答即可.
【解答】解:∵两个相似三角形的周长之比是1:2,
∴两个相似三角形的相似比是1:2,
∴它们的面积之比是:1:4,
故选:D.
8图中的两个三角形相似,且AB=2,A′B′=1,则△A′B′C′与△ABC的相似比是( )
A.1:2
B.2:1
C.3:1
D.1:3
【考点】相似三角形的性质.
【答案】A
【分析】根据相似三角形相似比等于对应边的比解答.
【解答】解:∵AB=2,A′B′=1,
∴△A′B′C′与△ABC的相似比=A′B′:AB=1:2.
故选:A.
二、填空题
9若△ABC∽△A′B′C′,且,若△ABC的面积为27cm2,则△A′B′C′的面积为
.
【考点】相似三角形的性质.
【专题】图形的相似;运算能力;推理能力.
【答案】48cm2.
【分析】根据相似三角形的面积之比等于相似比的平方,可以直接求出结果.
【解答】解:∵△ABC∽△A′B′C′,,
∴=()2=()2=,
即=,
解得:△A′B′C′的面积=48(cm2).
故答案为:48cm2.
10如图,如果△ABC∽△DAC,且AB=BC,则和∠C相等的角有
个.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】先根据相似三角形的判定定理求出△DAC也是等腰三角形,再根据相似三角形的对应角相等即可解答.
【解答】解:∵BC=AC,∴∠CAB=∠C,
又∵△ABC∽△DAC,∴△DAC也是等腰三角形,
∴AC=AD,∠C=∠DAC,
与∠C相等的角是∠DAC以及∠CAB共两个.
11已知图中的两个三角形相似,则x=
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】根据相似三角形的性质求解即可.
【解答】解:∵△ABC∽△A′B′C′,
∴BC:B′C′=AC:A′C′,
∴2:4=:x,
∴x=2.
故答案为2.
12已知△ABC∽△A′B′C′,且∠A=30°,∠B=40°,则∠C′=
度.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】利用相似三角形的对应角相等可求∠C.
【解答】解:∵△ABC∽△A′B′C′,且∠A=30°,∠B=40°,
∴∠A′=∠A=30°,∠B′=∠B=40°,
∴∠C′=110°.
13已知一个直角三角形的三边长分别是
3,10,14,与其相似的三角形的最长边是28,则这个三角形的周长等于
.
【考点】相似三角形的性质.
【专题】计算题.
【答案】见试题解答内容
【分析】先设所求三角形的周长是x,由于两个三角形相似,利用相似三角形周长比等于相似比可得关于x的方程,解即可.
【解答】解:设所求三角形的周长是x,
∵两个三角形相似,
∴=,
解得x=54.
故答案是54.
14如图,已知DE∥BC,△ADE∽△ABC,则=
=
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】△ADE∽△ABC根据相似三角形的对应边的比相等,得到==.
【解答】解:∵△ADE∽△ABC,∴==.
15已知△ABC的三边长之比是3:4:5,与其相似的△DEF的周长为18,则△DEF的面积为
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】判断出△ABC是直角三角形,然后根据相似比和周长求出各边长,求出△DEF的面积.
【解答】解:根据勾股定理逆定理,△DEF与△ABC均为直角三角形,设△DEF三边分别为3x,4x,5x则3x+4x+5x=18,x=三边长分别为:,6,,所以S△DEF=×6×=13.5.
16如图,若△ADE∽△ACB,AB=8,AE=4,DE=3,则BC=
.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】根据相似三角形的对应边的比相等列出比例式,计算即可.
【解答】解:∵△ADE∽△ACB,
∴=,即=,
解得,BC=6,
故答案为6.
三、解答题
17如图,已知△ABC∽△ACD,AC=6,AD=4,CD=2AD,求BD和BC的长.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】根据相似三角形的性质列出比例式,代入计算即可.
【解答】解:∵AD=4,CD=2AD,
∴CD=8,
∵△ABC∽△ACD,
∴==,即==,
解得,AB=9,BC=12,
∴BD=AB﹣AD=5.
18如图,△ABC与△ADB相似,AD=4,CD=6,求这两个三角形的相似比.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】先根据相似三角形对应边的比相等得出=,求出AB2=AC?AD=40,再根据相似比的定义即可求解.
【解答】解:∵△ABC与△ADB相似,
∴△ABC∽△ADB,
∴=,
∴AB2=AC?AD=10×4=40,
∴△ABC与△ADB的相似比为==.
19如图所示,△ABC∽△ADE,试说明△ABD∽△ACE.
【考点】相似三角形的判定与性质.
【专题】证明题.
【答案】见试题解答内容
【分析】由相似三角形的性质可知:,∠BAC=∠DAE,然后可证明∠BAD=∠CAE,最后依据相似三角形的判定定理进行证明即可.
【解答】证明:∵△ABC∽△ADE,
∴,∠BAC=∠DAE.
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.
∵且∠BAD=∠CAE,
∴△ABD∽△ACE.
20如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】由△ABC∽△ACD,且AD=5,BD=4,根据相似三角形的对应边成比例,可求得AC的长,继而求得答案.
【解答】解:∵AD=5,BD=4,
∴AB=AD+BD=9,
∵△ABC∽△ACD,
∴,
∴,
解得:AC=3,
∴△ACD与△ABC的相似比为:==.
21如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2.
(1)DE与AB的长度之比是多少?
(2)已知直角三角形ABC的周长是12cm,面积是6cm2,求直角三角形DEF的周长与面积.
【考点】相似三角形的性质.
【答案】见试题解答内容
【分析】根据相似三角形的对应边的比等于相似比,周长比等于相似比,面积比等于相似比的平方解题即可.
【解答】解:(1)由相似变换可得:DE:AB=DF:AC=2:3;
(2)∵AC:DF=3:2,
∴△DEF的周长:△ABC的周长=2:3,
S△DEF:S△ABC=4:9,
∵直角三角形ABC的周长是12cm,面积是6cm2
∴△DEF的周长为8cm,S△DEF=cm2.
22如图所示,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
【考点】相似三角形的性质.
【专题】压轴题;分类讨论.
【答案】见试题解答内容
【分析】由∠C=90°,BC=8cm,AC:AB=3:5,利用勾股定理即可求得AB与AC的长,然后设过t秒时,以C、P、Q为顶点的三角形恰与△ABC相似,则可得BP=2tcm,CP=BC﹣BP=8﹣2t(cm),CQ=tcm,再分别从当时,△CPQ∽△CBA与当时,△CPQ∽△CAB,去分析求解即可求得答案.
【解答】解:∵∠C=90°,BC=8cm,AC:AB=3:5,
∴设AC=3xcm,AB=5xcm,
则BC==4x(cm),
即4x=8,
解得:x=2,
∴AC=6cm,AB=10cm,
∴BC=8cm,
设过t秒时,以C、P、Q为顶点的三角形恰与△ABC相似,
则BP=2tcm,CP=BC﹣BP=8﹣2t(cm),CQ=tcm,
∵∠C是公共角,
∴①当,即时,△CPQ∽△CBA,
解得:t=2.4,
②当,即时,△CPQ∽△CAB,
解得:t=,
∴过2.4或秒时,以C、P、Q为顶点的三角形恰与△ABC相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
