1.2矩形的性质与判定培优提升训练 2021-2022学年北师大版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.2矩形的性质与判定培优提升训练 2021-2022学年北师大版九年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 257.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 00:00:00 | ||
图片预览





文档简介
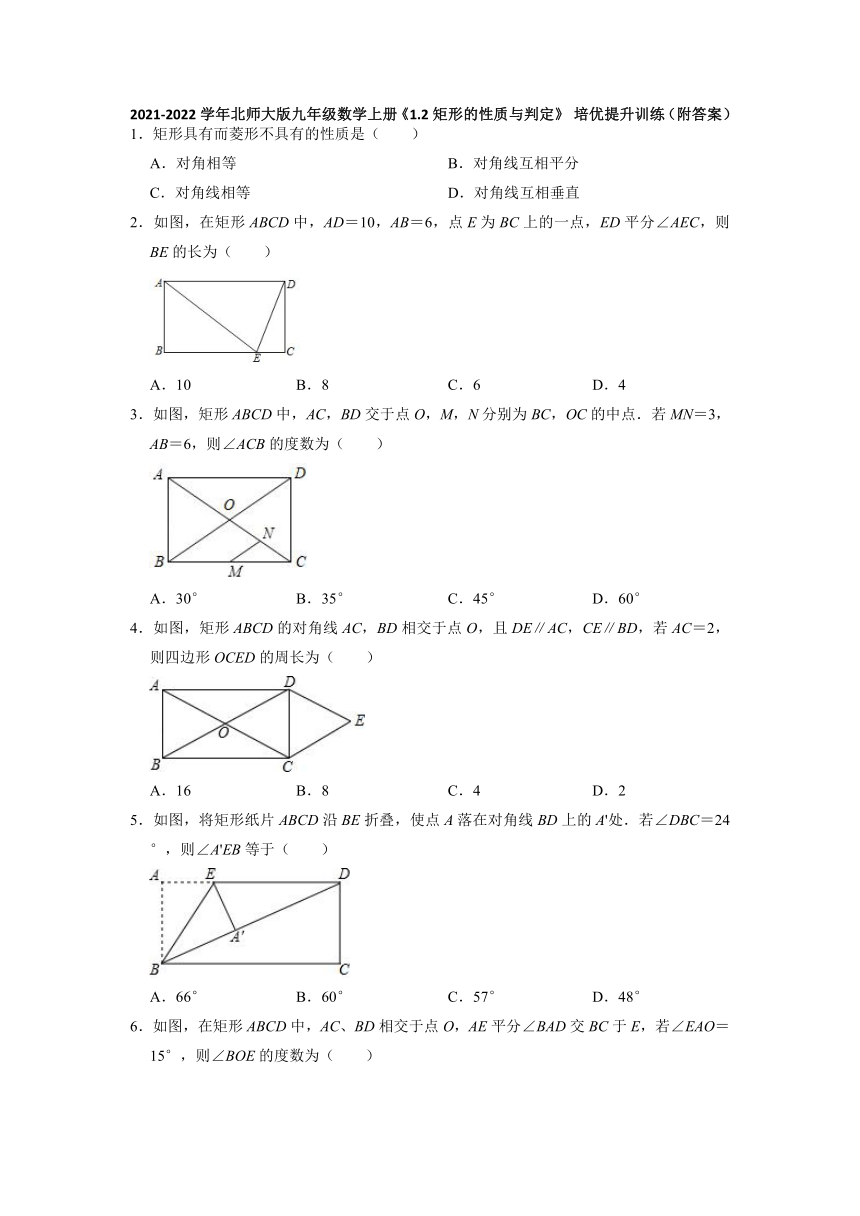
2021-2022学年北师大版九年级数学上册《1.2矩形的性质与判定》
培优提升训练(附答案)
1.矩形具有而菱形不具有的性质是( )
A.对角相等
B.对角线互相平分
C.对角线相等
D.对角线互相垂直
2.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10
B.8
C.6
D.4
3.如图,矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点.若MN=3,AB=6,则∠ACB的度数为( )
A.30°
B.35°
C.45°
D.60°
4.如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=2,则四边形OCED的周长为( )
A.16
B.8
C.4
D.2
5.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66°
B.60°
C.57°
D.48°
6.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
A.85°
B.80°
C.75°
D.70°
7.如图,点M是矩形ABCD的对角线AC上一点,过点M作EF∥AB,分别交AD,BC于点E,F,连接MD,MB.若DE=2,EM=5,则阴影部分的面积为( )
A.5
B.10
C.12
D.14
8.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任意一点过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是( )
A.2
B.2.4
C.3
D.4
9.如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )
A.
B.
C.12
D.32
10.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,如果∠ABD=60°,那么∠BAE的度数是( )
A.40°
B.55°
C.75°
D.80°
11.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
A.
B.
C.
D.
12.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为( )
A.4
B.6
C.2
D.
13.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=
°.
14.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为
.
15.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是S1
S2(填“>”“<”或“=”)
16.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=2,BC=6,则OB的长为
.
17.如图,菱形ABCD的对角线AC,BD交于点O,且BE∥AC,AE∥BD,连接EO.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若CD=6,求OE的长.
18.如图,在?ABCD中,延长AB到点E,使BE=AB,DE交BC于点O,连接EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=40°,当∠BOD等于多少度时四边形BECD是矩形,并说明理由.
19.如图,在矩形ABCD中,EF垂直平分BD,分别交AD、BD、BC于点E、O、F,连接BE、DF.
(1)求证:四边形BEDF是菱形;
(2)若AB=6,BD=10,求EF的长.
20.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为8,∠ABC=60°,求AE的长.
参考答案
1.解:矩形的性质是:①矩形的四个角都是直角,②矩形的对边相等且互相平行,③矩形对角线相等且互相平分;
菱形的性质是:①菱形的四条边都相等,菱形的对边互相平行;②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每条对角线平分一组对角,
所以矩形具有而菱形不具有的性质是对角线相等,
故选:C.
2.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
又∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=10,
在直角△ABE中,BE==8.
故选:B.
3.解:∵M、N分别为BC、OC的中点,
∴BO=2MN=6.
∵四边形ABCD是矩形,
∴AC=BD=2BO=12,
==,
∴∠ACB=30°,
故选:A.
4.解:∵四边形ABCD为矩形,
∴OA=OC,OB=OD,且AC=BD=2,
∴OA=OB=OC=OD=1,
∵CE∥BD,DE∥AC,
∴四边形DECO为平行四边形,
∵OD=OC,
∴四边形DECO为菱形,
∴OD=DE=EC=OC=1,
则四边形OCED的周长为1+1+1+1=4,
故选:C.
5.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
6.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90﹣60°=30°,OB=BE,
∴∠BOE=(180°﹣30°)=75°.
故选:C.
7.解:作PM⊥AB于P,交DC于Q.
则有四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC﹣S△AMP﹣S△MCF=S△ADC﹣S△AEM﹣S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×5=5,
∴S阴=5+5=10,
故选:B.
8.解:连接CP,
∵PE⊥AC,PF⊥BC,∠ACB=90°,
∴∠PEC=∠ACB=∠PFC=90°,
∴四边形PECF是矩形,
∴EF=CP,
当CP⊥AB时,CP最小,即EF最小,
在Rt△ABC中,∠C=90°,AC=3,BC=4,由勾股定理得:AB=5,
由三角形面积公式得:AC×BC=AB×CP,
CP=,
即EF的最小值是=2.4,
故选:B.
9.解:连接AE,如图所示:
∵四边形ABCD是矩形,
∴OA=OC,∠ABC=90°,BC=AD=4,
∵OE⊥AC,
∴AE=CE=3,
∴BE=BC﹣CE=1,
∴AB===2,
∴矩形ABCD的面积=AB×BC=2×4=8;
故选:B.
10.解:连接AC,
∵四边形ABCD是矩形,
∴AD∥BE,AC=BD,∠BAD=90°,∠ABD=∠BAC=60°,
∴∠E=∠DAE,∠CAD=∠BAD﹣∠BAC=90°﹣60°=30°,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠CAD=∠CAE+∠DAE,
∴∠E+∠E=30°,即∠E=15°.
∴∠BAE=90°﹣15°=75°,
故选:C.
11.解:∵AB=6,BC=8,
∴矩形ABCD的面积为48,AC==10,
∴AO=DO=AC=5,
∵对角线AC,BD交于点O,
∴△AOD的面积为12,
∵EO⊥AO,EF⊥DO,
∴S△AOD=S△AOE+S△DOE,即12=AO×EO+DO×EF,
∴12=×5×EO+×5×EF,
∴5(EO+EF)=24,
∴EO+EF=,
故选:C.
12.解:如图,连接AE,设EF与AC交点为O,
∵EF是AC的垂直平分线,
∴OA=OC,AE=CE,
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE=6,
∴AE=CE=6,BC=BE+CE=4+6=10,
∴AB===2,
∴AC===2,
故选:C.
13.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故答案为:35.
14.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
15.解:矩形ABCD的面积S=2S△ABC,而S△ABC=S矩形AEFC,即S1=S2,
故答案为:=.
16.解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,OM∥AB,
∴OM是△ADC的中位线,
∵OM=2,
∴DC=4,
∵AD=BC=6,
∴AC==2,
∴BO=AC=,
故答案为:
17.解:(1)四边形AEBO是矩形.
理由:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形,
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,
即∠AOB=90°,
∴四边形AEBO是矩形;
(2)∵四边形AEBO是矩形,
∴EO=AB,
∵四边形ABCD是菱形,
∴AB=CD.
∴EO=CD=6.
18.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形;
(2)解:若∠A=40°,当∠BOD=80°时,四边形BECD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=40°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=80°﹣40°=40°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形.
19.证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠EDO=∠OBF,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=90°,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴四边形EBFD是平行四边形,
又∵EF⊥BD,
∴四边形EBFD是菱形;
(2)∵四边形EBFD是菱形,
∴ED=EB,
∵AB=6,BD=10,
∴AD===8,
设AE=x,则ED=EB=8﹣x,
在Rt△ABE中,BE2﹣AB2=AE2,
即(8﹣x)2=x2+62,
∴x=,
∴DE=8﹣=,
∴EO===,
∴EF=2EO=.
20.解:(1)在菱形ABCD中,OC=AC,AC⊥BD.
又∵DE=AC,
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵∠COD=90°,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,AB=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=8,AO=4.
∴在矩形OCED中,CE=OD==4.
又∵矩形DOCE中,∠OCE=90°,
∴在Rt△ACE中,AE===4.
培优提升训练(附答案)
1.矩形具有而菱形不具有的性质是( )
A.对角相等
B.对角线互相平分
C.对角线相等
D.对角线互相垂直
2.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10
B.8
C.6
D.4
3.如图,矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点.若MN=3,AB=6,则∠ACB的度数为( )
A.30°
B.35°
C.45°
D.60°
4.如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD,若AC=2,则四边形OCED的周长为( )
A.16
B.8
C.4
D.2
5.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66°
B.60°
C.57°
D.48°
6.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
A.85°
B.80°
C.75°
D.70°
7.如图,点M是矩形ABCD的对角线AC上一点,过点M作EF∥AB,分别交AD,BC于点E,F,连接MD,MB.若DE=2,EM=5,则阴影部分的面积为( )
A.5
B.10
C.12
D.14
8.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任意一点过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是( )
A.2
B.2.4
C.3
D.4
9.如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )
A.
B.
C.12
D.32
10.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,如果∠ABD=60°,那么∠BAE的度数是( )
A.40°
B.55°
C.75°
D.80°
11.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
A.
B.
C.
D.
12.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为( )
A.4
B.6
C.2
D.
13.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=
°.
14.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为
.
15.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是S1
S2(填“>”“<”或“=”)
16.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=2,BC=6,则OB的长为
.
17.如图,菱形ABCD的对角线AC,BD交于点O,且BE∥AC,AE∥BD,连接EO.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若CD=6,求OE的长.
18.如图,在?ABCD中,延长AB到点E,使BE=AB,DE交BC于点O,连接EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=40°,当∠BOD等于多少度时四边形BECD是矩形,并说明理由.
19.如图,在矩形ABCD中,EF垂直平分BD,分别交AD、BD、BC于点E、O、F,连接BE、DF.
(1)求证:四边形BEDF是菱形;
(2)若AB=6,BD=10,求EF的长.
20.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为8,∠ABC=60°,求AE的长.
参考答案
1.解:矩形的性质是:①矩形的四个角都是直角,②矩形的对边相等且互相平行,③矩形对角线相等且互相平分;
菱形的性质是:①菱形的四条边都相等,菱形的对边互相平行;②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每条对角线平分一组对角,
所以矩形具有而菱形不具有的性质是对角线相等,
故选:C.
2.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
又∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=10,
在直角△ABE中,BE==8.
故选:B.
3.解:∵M、N分别为BC、OC的中点,
∴BO=2MN=6.
∵四边形ABCD是矩形,
∴AC=BD=2BO=12,
==,
∴∠ACB=30°,
故选:A.
4.解:∵四边形ABCD为矩形,
∴OA=OC,OB=OD,且AC=BD=2,
∴OA=OB=OC=OD=1,
∵CE∥BD,DE∥AC,
∴四边形DECO为平行四边形,
∵OD=OC,
∴四边形DECO为菱形,
∴OD=DE=EC=OC=1,
则四边形OCED的周长为1+1+1+1=4,
故选:C.
5.解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
6.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90﹣60°=30°,OB=BE,
∴∠BOE=(180°﹣30°)=75°.
故选:C.
7.解:作PM⊥AB于P,交DC于Q.
则有四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC﹣S△AMP﹣S△MCF=S△ADC﹣S△AEM﹣S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×5=5,
∴S阴=5+5=10,
故选:B.
8.解:连接CP,
∵PE⊥AC,PF⊥BC,∠ACB=90°,
∴∠PEC=∠ACB=∠PFC=90°,
∴四边形PECF是矩形,
∴EF=CP,
当CP⊥AB时,CP最小,即EF最小,
在Rt△ABC中,∠C=90°,AC=3,BC=4,由勾股定理得:AB=5,
由三角形面积公式得:AC×BC=AB×CP,
CP=,
即EF的最小值是=2.4,
故选:B.
9.解:连接AE,如图所示:
∵四边形ABCD是矩形,
∴OA=OC,∠ABC=90°,BC=AD=4,
∵OE⊥AC,
∴AE=CE=3,
∴BE=BC﹣CE=1,
∴AB===2,
∴矩形ABCD的面积=AB×BC=2×4=8;
故选:B.
10.解:连接AC,
∵四边形ABCD是矩形,
∴AD∥BE,AC=BD,∠BAD=90°,∠ABD=∠BAC=60°,
∴∠E=∠DAE,∠CAD=∠BAD﹣∠BAC=90°﹣60°=30°,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠CAD=∠CAE+∠DAE,
∴∠E+∠E=30°,即∠E=15°.
∴∠BAE=90°﹣15°=75°,
故选:C.
11.解:∵AB=6,BC=8,
∴矩形ABCD的面积为48,AC==10,
∴AO=DO=AC=5,
∵对角线AC,BD交于点O,
∴△AOD的面积为12,
∵EO⊥AO,EF⊥DO,
∴S△AOD=S△AOE+S△DOE,即12=AO×EO+DO×EF,
∴12=×5×EO+×5×EF,
∴5(EO+EF)=24,
∴EO+EF=,
故选:C.
12.解:如图,连接AE,设EF与AC交点为O,
∵EF是AC的垂直平分线,
∴OA=OC,AE=CE,
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE=6,
∴AE=CE=6,BC=BE+CE=4+6=10,
∴AB===2,
∴AC===2,
故选:C.
13.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故答案为:35.
14.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
15.解:矩形ABCD的面积S=2S△ABC,而S△ABC=S矩形AEFC,即S1=S2,
故答案为:=.
16.解:∵四边形ABCD是矩形,
∴∠D=90°,
∵O是矩形ABCD的对角线AC的中点,OM∥AB,
∴OM是△ADC的中位线,
∵OM=2,
∴DC=4,
∵AD=BC=6,
∴AC==2,
∴BO=AC=,
故答案为:
17.解:(1)四边形AEBO是矩形.
理由:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形,
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,
即∠AOB=90°,
∴四边形AEBO是矩形;
(2)∵四边形AEBO是矩形,
∴EO=AB,
∵四边形ABCD是菱形,
∴AB=CD.
∴EO=CD=6.
18.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形;
(2)解:若∠A=40°,当∠BOD=80°时,四边形BECD是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=40°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=80°﹣40°=40°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形.
19.证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠EDO=∠OBF,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=90°,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∴四边形EBFD是平行四边形,
又∵EF⊥BD,
∴四边形EBFD是菱形;
(2)∵四边形EBFD是菱形,
∴ED=EB,
∵AB=6,BD=10,
∴AD===8,
设AE=x,则ED=EB=8﹣x,
在Rt△ABE中,BE2﹣AB2=AE2,
即(8﹣x)2=x2+62,
∴x=,
∴DE=8﹣=,
∴EO===,
∴EF=2EO=.
20.解:(1)在菱形ABCD中,OC=AC,AC⊥BD.
又∵DE=AC,
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵∠COD=90°,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,AB=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=8,AO=4.
∴在矩形OCED中,CE=OD==4.
又∵矩形DOCE中,∠OCE=90°,
∴在Rt△ACE中,AE===4.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
