2019-2020学年山东省烟台市龙口市七年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2019-2020学年山东省烟台市龙口市七年级(下)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 861.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 00:00:00 | ||
图片预览




文档简介
2019-2020学年山东省烟台市龙口市七年级(下)期末数学试卷(五四学制)
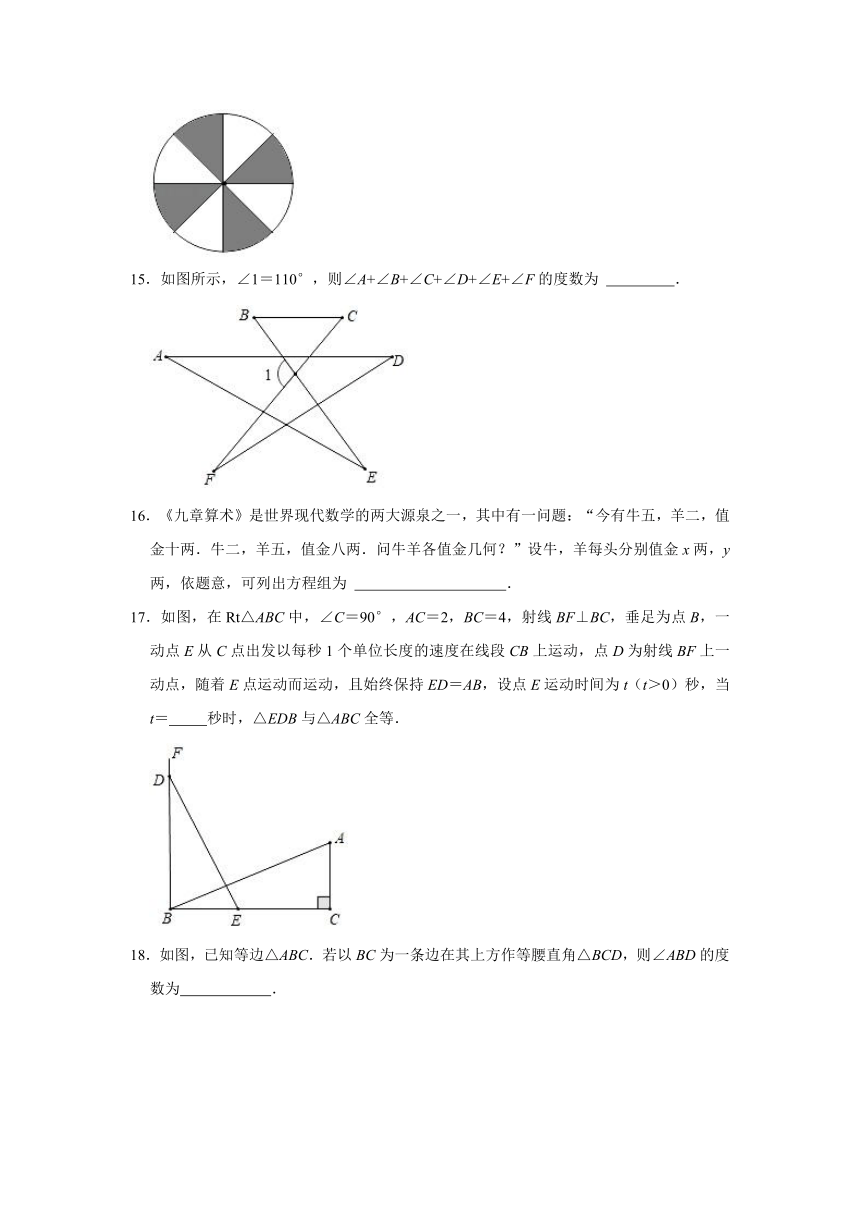
一、选择题(共12小题).
1.若a>b,则下列不等式正确的是( )
A.3a<3b
B.ma>mb
C.﹣a﹣1>﹣b﹣1
D.+1>+1
2.下列语句是真命题的是( )
A.作∠AOB的平分线
B.若a2=b2,则a=b
C.四边形的内角和等于360°
D.不是对顶角不相等
3.下列描述的事件中,是随机事件的为( )
A.水能载舟,亦能覆舟
B.心想事成,万事如意
C.瓜熟蒂落,水到渠成
D.只手遮天,偷天换日
4.在一个不透明的盒子中装有n个球,其中红球有5个,它们除颜色外其它均相同.每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.05,那么可以推算出n的值大约是( )
A.100
B.500
C.1000
D.无法判断
5.如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F.若AB=DE,BC=BE,AC=BD,则∠ACB等于( )
A.∠E
B.∠D
C.∠BFC
D.∠DBE
6.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=70°,则∠1=( )
A.40°
B.20°
C.60°
D.70°
7.如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量相差( )
A.8g
B.10g
C.12g
D.15g
8.如图,已知∠ABC=60°,点D在边BA上,BD=10,点E,F在边BC上,DE=DF,若EF=4,则BE的长为( )
A.3
B.2.5
C.2
D.1.5
9.如图,AB∥CD,∠ABE=40°,若CF平分∠ECD,且满足CF∥BE,则∠ECD的度数为( )
A.70°
B.74°
C.78°
D.80°
10.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AE=AF;②AD垂直平分EF;③EF垂直平分AD;④AD平分∠EDF.其中正确的结论的个数为( )
A.1
B.2
C.3
D.4
11.如图,一张△ABC的纸片中,∠ACB=90°,BC=6,AB=10.在AC边上取一点E,将其沿着BE折叠,使点A与BC延长线上的点D重合,则CE的长为( )
A.4
B.3
C.2
D.1
12.如图,直线y=ax+4a(a≠0)与y=﹣x+b的交点的横坐标为﹣2,则关于x的不等式﹣x+b>ax+4a>0的整数解为( )
A.﹣1
B.﹣3
C.﹣4
D.﹣5
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.已知二元一次方程2x﹣7y=5,用含x的代数式表示y的等式为
.
14.“六一”节,小明去公园玩投掷飞镖的游戏.如图,圆形镖盘被等分成8部分,投中图中阴影部分有奖品.小明能获得奖品的概率是
.
15.如图所示,∠1=110°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
.
16.《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五,羊二,值金十两.牛二,羊五,值金八两.问牛羊各值金几何?”设牛,羊每头分别值金x两,y两,依题意,可列出方程组为
.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,射线BF⊥BC,垂足为点B,一动点E从C点出发以每秒1个单位长度的速度在线段CB上运动,点D为射线BF上一动点,随着E点运动而运动,且始终保持ED=AB,设点E运动时间为t(t>0)秒,当t=
秒时,△EDB与△ABC全等.
18.如图,已知等边△ABC.若以BC为一条边在其上方作等腰直角△BCD,则∠ABD的度数为
.
三、解答题(本大题共8个小题,满分66分)
19.解方程组.
20.解不等式组,然后把解集在数轴上表示出来,并写出不等式组的整数解.
21.在解关于x,y的方程组时,可以用①×7﹣②×3消去未知数x,也可以用①×2+②×5消去未知数y.
(1)求m和n的值;
(2)求原方程组的解.
22.如图,已知DE∥BC,∠3=∠B,求证:∠1+∠2=180°.
下面是小明同学不完整的证明过程,请你在横线上补充完整,并在括号里填上每一步的推理依据.
证明:∵DE∥BC(已知),
∴∠3=
(
).
∵∠3=∠B(
),
∴
=∠EHC(
).
∴AB∥EH(
).
∴∠2+
=180°(两直线平行,同旁内角互补).
∵∠1=∠4(
),
∴∠1+∠2=180°(
).
23.一个不透明袋子中装有红、黄、绿三种颜色的球共60个,它们除颜色外都相同.已知其中黄球个数是绿球个数的4倍,从袋中摸出一个球是红球的概率为.
(1)分别求红球和绿球的个数.
(2)求从袋中随机摸出一球是绿球的概率.
(3)从袋中拿出12个黄球,将剩余的球搅拌均匀,求从袋中剩余的球中随机摸出一个球是黄球的概率.
24.如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟时,甲、乙两人相距多少千米?
25.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
26.如图,△ABC与△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,连接BD,过点A作AF⊥BD交BD的延长线于点F.
(1)若AB=10,求四边形ADBE的面积;
(2)求证:BC=2AF.
参考答案
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1.若a>b,则下列不等式正确的是( )
A.3a<3b
B.ma>mb
C.﹣a﹣1>﹣b﹣1
D.+1>+1
【分析】根据不等式的性质逐一判断,判断出正确的不等式是哪个即可.
解:∵a>b,
∴3a>3b,
∴选项A不正确;
∵a>b,
∴m<0时,ma<mb;m=0时,ma=mb;m>0时,ma>mb,
∴选项B不正确;
∵a>b,
∴﹣a<﹣b,
∴﹣a﹣1<﹣b﹣1,
∴选项C不正确;
∵a>b,
∴>,
∴+1>+1,
∴选项D正确.
故选:D.
2.下列语句是真命题的是( )
A.作∠AOB的平分线
B.若a2=b2,则a=b
C.四边形的内角和等于360°
D.不是对顶角不相等
【分析】根据命题的概念、四边形的性质、对顶角的概念判断即可.
解:A、作∠AOB的平分线,没有对事件作出判断,不是命题,不符合题意;
B、若a2=b2,则a=±b,故原命题错误,是真命题,符合题意;
C、四边形的内角和为360°,本选项说法正确,是真命题,符合题意;
D、不是对顶角也可以相等,故本选项说法错误,是假命题,不符合题意;
故选:C.
3.下列描述的事件中,是随机事件的为( )
A.水能载舟,亦能覆舟
B.心想事成,万事如意
C.瓜熟蒂落,水到渠成
D.只手遮天,偷天换日
【分析】直接利用随机事件以及必然事件、不可能事件的定义分别分析得出答案.
解:A、水能载舟,亦能覆舟,是必然事件,故此选项不符合题意;
B、心想事成,万事如意,是随机事件,故此选项符合题意;
C、瓜熟蒂落,水到渠成,是必然事件,故此选项不符合题意;
D、只手遮天,偷天换日,是不可能事件,故此选项不符合题意.
故选:B.
4.在一个不透明的盒子中装有n个球,其中红球有5个,它们除颜色外其它均相同.每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.05,那么可以推算出n的值大约是( )
A.100
B.500
C.1000
D.无法判断
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解即可.
解:由题意可得,=0.05,
解得,n=100.
故估计n大约是100.
故选:A.
5.如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F.若AB=DE,BC=BE,AC=BD,则∠ACB等于( )
A.∠E
B.∠D
C.∠BFC
D.∠DBE
【分析】先根据SSS定理得出△ABC≌△DEB(SSS),即可根据全等三角形的性质得到∠ACB=∠DBE.
解:在△ABC与△DEB中,
,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE,
故选:D.
6.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=70°,则∠1=( )
A.40°
B.20°
C.60°
D.70°
【分析】先由题意可得:AB=AC,根据等边对等角的性质,可求得∠ACB的度数,又由直线l1∥l2,根据两直线平行,同旁内角互补即可求得∠1的度数.
解:根据题意得:AB=AC,
∴∠ACB=∠ABC=70°,
∵直线l1∥l2,
∴∠1+∠ACB+∠ABC=180°,
∴∠1=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°.
故选:A.
7.如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量相差( )
A.8g
B.10g
C.12g
D.15g
【分析】根据图可得:3块巧克力的重=2个果冻的重;1块巧克力的重+1个果冻的重=40g,由此可设出未知数,列出方程组解答.
解:设每块巧克力的重xg,每个果冻的重yg,由题意得:
,
解得:.
所以y﹣x=24﹣16=8(g),
即每块巧克力和每个果冻的重量相差8g.
故选:A.
8.如图,已知∠ABC=60°,点D在边BA上,BD=10,点E,F在边BC上,DE=DF,若EF=4,则BE的长为( )
A.3
B.2.5
C.2
D.1.5
【分析】过点D作DG⊥BC,垂足为G.利用等腰三角形的“三线合一”先求出EG,利用含30°角的直角三角形的边间关系,再求出BG,最后利用线段的和差关系求出BE.
解:过点D作DG⊥BC,垂足为G.
∵DE=DF,DG⊥BC,EF=4,
∴EG=EF=2.
在Rt△DBG中,∵∠ABC=60°,
∴∠BDG=30°.
∵DB=10,
∴BG=DB=5.
∴BE=BG﹣EG=3.
故选:A.
9.如图,AB∥CD,∠ABE=40°,若CF平分∠ECD,且满足CF∥BE,则∠ECD的度数为( )
A.70°
B.74°
C.78°
D.80°
【分析】如图,过E作EM∥AB,由EM∥AB,得∠B=∠BEM=40°.由AB∥CD,得EM∥CD,那么∠MEC+∠ECD=180°.由CF平分∠ECD,得∠ECF=.由BE∥CF,得∠BEC+∠ECF=180°,那么∠BEM+∠MEC+∠ECF=180°,故40°+180°﹣∠ECD+=180°,进而解决此题.
解:如图,过E作EM∥AB.
∵EM∥AB,
∴∠B=∠BEM=40°.
又∵AB∥CD,
∴EM∥CD.
∴∠MEC+∠ECD=180°.
∴∠MEC=180°﹣∠ECD.
∵CF平分∠ECD,
∴∠ECF=.
∵BE∥CF,
∴∠BEC+∠ECF=180°.
∴∠BEM+∠MEC+∠ECF=180°.
∴40°+180°﹣∠ECD+=180°.
∴∠ECD=80°.
故选:D.
10.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AE=AF;②AD垂直平分EF;③EF垂直平分AD;④AD平分∠EDF.其中正确的结论的个数为( )
A.1
B.2
C.3
D.4
【分析】根据角平分线性质求出DE=DF,证△AED≌△AFD,推出AE=AF,再逐个判断即可.
解:∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,∠ADE=∠ADF,
∴AD平分∠EDF;④正确;
∵AD平分∠BAC,
∵AE=AF,DE=DF,①正确;
∴AD垂直平分EF,②正确;③错误,
正确的有3个,
故选:C.
11.如图,一张△ABC的纸片中,∠ACB=90°,BC=6,AB=10.在AC边上取一点E,将其沿着BE折叠,使点A与BC延长线上的点D重合,则CE的长为( )
A.4
B.3
C.2
D.1
【分析】由勾股定理可求AC的长,由折叠的性质可得,BD=AB=10,EA=ED,利用勾股定理列方程求解即可.
解:由勾股定理得,AC===8,
由折叠的性质可得,BD=AB=10,EA=ED,
∴CD=BD﹣BC=10﹣6=4,
设CE=x,则EA=ED=8﹣x,
在Rt△DCE中,由勾股定理得,
x2+42=(8﹣x)2,
∴x=3,
故选:B.
12.如图,直线y=ax+4a(a≠0)与y=﹣x+b的交点的横坐标为﹣2,则关于x的不等式﹣x+b>ax+4a>0的整数解为( )
A.﹣1
B.﹣3
C.﹣4
D.﹣5
【分析】满足不等式﹣x+b>ax+4a>0就是直线y=﹣x+b位于直线y=ax+4a的上方且位于x轴的上方的图象,据此求得自变量的取值范围即可.
解:∵直线y=ax+4a(a≠0)与y=﹣x+b的交点的横坐标为﹣2,
∴关于x的不等式﹣x+b>ax+4a的解集为x<﹣2,
∵y=ax+4a=0时,x=﹣4,
∴ax+4a>0的解集是x>﹣4,
∴﹣x+b>ax+4a>0的解集是﹣4<x<﹣2,
∴关于x的不等式式﹣x+b>ax+4a>0的整数解为﹣3.
故选:B.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.已知二元一次方程2x﹣7y=5,用含x的代数式表示y的等式为
y= .
【分析】先移项,再把y的系数化为1即可.
解:移项得,7y=2x﹣5,
y的系数化为1得,y=.
故答案为:y=.
14.“六一”节,小明去公园玩投掷飞镖的游戏.如图,圆形镖盘被等分成8部分,投中图中阴影部分有奖品.小明能获得奖品的概率是
.
【分析】用阴影部分的份数除以总份数即可求得获得奖品的概率.
解:∵飞镖盘被平均分成8份,阴影部分占4份,
∴小明能获得奖品的概率是=.
故答案为:.
15.如图所示,∠1=110°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
220° .
【分析】连接EF,由三角形的内角和定理可求得∠A+∠D+∠CFD+∠AEB=∠BEF+∠CFE,利用三角形外角的性质可得∠1=∠B+∠C=∠BEF+∠CFE=∠A+∠D+∠CFD+∠AEB,进而可求解.
解:连接EF,
∵∠A+∠D+∠3=∠AEF+∠DFE+∠2=180°,∠2=∠3,
∴∠A+∠D=∠AEF+∠DFE,
∴∠A+∠D+∠CFD+∠AEB=∠AEF+∠DFE+∠CFD+∠AEB=∠BEF+∠CFE,
∵∠1=∠B+∠C=∠BEF+∠CFE,
∴∠A+∠D+∠CFD+∠AEB=∠1,
∵∠1=110°,
∴∠A+∠B+∠C+∠D+∠AEB+∠CFD=2∠1=220°,
16.《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五,羊二,值金十两.牛二,羊五,值金八两.问牛羊各值金几何?”设牛,羊每头分别值金x两,y两,依题意,可列出方程组为
.
【分析】因为每头牛值金x两,每头羊值金y两,根据“牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两”,即可得出关于x、y的二元一次方程组,此题得解.
解:因为每头牛值金x两,每头羊值金y两,
根据题意得:.
故答案为:.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,射线BF⊥BC,垂足为点B,一动点E从C点出发以每秒1个单位长度的速度在线段CB上运动,点D为射线BF上一动点,随着E点运动而运动,且始终保持ED=AB,设点E运动时间为t(t>0)秒,当t= 2 秒时,△EDB与△ABC全等.
【分析】当BE=CA或BE=CB时,由HL得△EDB与△ABC全等,则4﹣t=2或4﹣t=4,即可求解.
解:∵BF⊥BC,
∴∠EBD=90°,
∵∠ACB=90°,ED=AB,
∴当BE=CA或BE=CB时,△EDB与△ABC全等,
∴4﹣t=2或4﹣t=4,
解得:t=2或t=0,
∵t>0,
∴t=2,
即当t=2秒时,△EDB与△ABC全等,
故答案为:2.
18.如图,已知等边△ABC.若以BC为一条边在其上方作等腰直角△BCD,则∠ABD的度数为 15°或30° .
【分析】分情况讨论,分别以BC为底边或腰在其上方作等腰直角△BCD,分别画图,即可得到∠ABD的度数.
解:如图1所示,∠ABD=∠CBD﹣∠ABC=90°﹣60°=30°;
如图2所示,∠ABD=∠ABC﹣∠DBC=60°﹣45°=15°;
如图3所示,∠ABD=∠ABC﹣∠DBC=60°﹣45°=15°;
故答案为:15°或30°.
三、解答题(本大题共8个小题,满分66分)
19.解方程组.
【分析】方程组利用代入消元法求出解即可.
解:,
将①代入②得:11x=33,
解得:x=3,
将x=3代入①得:y=3,
则方程组的解为.
20.解不等式组,然后把解集在数轴上表示出来,并写出不等式组的整数解.
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分求出不等式组的解集,表示在数轴上,确定出整数解即可.
解:,
由①得,x>﹣2,
由②得,x≤1,
∴不等式组的解集是﹣2<x≤1,
解集在数轴上表示如图:
∴不等式组的整数解是﹣1,0,1.
21.在解关于x,y的方程组时,可以用①×7﹣②×3消去未知数x,也可以用①×2+②×5消去未知数y.
(1)求m和n的值;
(2)求原方程组的解.
【分析】(1)利用①×7﹣②×3消去未知数x得到7(m+1)=3(n+2),利用①×2+②×5得到﹣2n+5m=0,然后解关于m、n的方程组即可;
(2)由(1)得到,然后利用加减消元法解方程组.
解:(1)根据题意得,解得;
(2)原方程组为,
①×7﹣②×3得﹣35y﹣6y=123,
解得y=﹣3,
把y=﹣3代入②得7x﹣6=1,
解得x=1,
所以原方程组的解为.
22.如图,已知DE∥BC,∠3=∠B,求证:∠1+∠2=180°.
下面是小明同学不完整的证明过程,请你在横线上补充完整,并在括号里填上每一步的推理依据.
证明:∵DE∥BC(已知),
∴∠3= ∠EHC (
两直线平行,内错角相等 ).
∵∠3=∠B(
已知 ),
∴ ∠B =∠EHC(
等量代换 ).
∴AB∥EH(
同位角相等,两直线平行 ).
∴∠2+ ∠4 =180°(两直线平行,同旁内角互补).
∵∠1=∠4(
对顶角相等 ),
∴∠1+∠2=180°(
等量代换 ).
【分析】由平行线的性质可得∠3=∠EHC,从而有∠B=∠EHC,则可判断AB∥EH,根据平行线的性质有∠2+∠4=180°,即可得证.
【解答】证明:∵DE∥BC(已知),
∴∠3=∠EHC(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠EHC(等量代换),
∴AB∥EH(同位角相等,两直线平行),
∴∠2+∠4=180°(两直线平行,同旁内角互补),
∵∠1=∠4(对顶角相等),
∴∠1+∠2=180°(等量代换).
故答案为:∠EHC;两直线平行,内错角相等;已知;等量代换;同位角相等,两直线平行;∠4;对顶角相等;等量代换.
23.一个不透明袋子中装有红、黄、绿三种颜色的球共60个,它们除颜色外都相同.已知其中黄球个数是绿球个数的4倍,从袋中摸出一个球是红球的概率为.
(1)分别求红球和绿球的个数.
(2)求从袋中随机摸出一球是绿球的概率.
(3)从袋中拿出12个黄球,将剩余的球搅拌均匀,求从袋中剩余的球中随机摸出一个球是黄球的概率.
【分析】(1)根据红、黄、白三种颜色球共有的个数乘以红球的概率即可求得红球的个数,设绿球有x个,则黄球有2x个,根据球的总个数列出方程求出x的值即可得;
(2)用绿球的个数除以总的球数即可;
(3)先求出从袋中拿出4个黄球还剩的球数,再根据红球的个数,除以还剩的球数即可.
解:(1)红球个数:60×=20(个),
设绿球有x个,则黄球有4x个,
根据题意,得x+4x+20=60,
解得x=8,
所以红球有20个,绿球有8个,
(2)从袋中随机摸出一球,共有60种等可能的结果,其中摸出绿球的结果有8种,
所以从袋中随机摸出一球是绿球的概率为=;
(3)由(1)得4x=32,拿出12个黄球以后,从袋中随机摸出一球,共有48种等可能的结果,其中摸出黄球的结果有20种,
所以从袋中剩余的球中随机摸出一个球是黄球的概率=.
24.如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟时,甲、乙两人相距多少千米?
【分析】(1)分别根据甲、乙的图象计算出各自的速度即可求出S甲、S乙与t之间的关系式;
(2)把t=10代入解析式进而解答即可.
解:(1)由图象设甲的解析式为:S甲=kt,代入点(24,12),解得:k=0.5;
所以甲的解析式为:S甲=0.5t;
同理可设乙的解析式为:S乙=mt+b,代入点(6,0),(18,12),
可得:,
解得:,
所以乙的解析式为S乙=t﹣6;
(2)当t=10时,S甲=0.5×10=5(千米),S乙=10﹣6=4(千米),
5﹣4=1(千米),
答:甲行驶10分钟时,甲、乙两人相距1千米.
25.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【分析】(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号4台B型号的电扇收入1200元,5台A型号6台B型号的电扇收入1900元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台,根据金额不多余7500元,列不等式求解;
(3)根据A种型号电风扇的进价和售价、B种型号电风扇的进价和售价以及总利润=一台的利润×总台数,列出不等式,求出a的值,再根据a为整数,即可得出答案.
解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:,
解得:,
答:A、B两种型号电风扇的销售单价分别为200元、150元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台.
依题意得:160a+120(50﹣a)≤7500,
解得:a≤37.
答:超市最多采购A种型号电风扇37台时,采购金额不多于7500元.
(3)根据题意得:
(200﹣160)a+(150﹣120)(50﹣a)>1850,
解得:a>35,
∵a≤37,且a应为整数,
∴在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种:
当a=36时,采购A种型号的电风扇36台,B种型号的电风扇14台;
当a=37时,采购A种型号的电风扇37台,B种型号的电风扇13台.
26.如图,△ABC与△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,连接BD,过点A作AF⊥BD交BD的延长线于点F.
(1)若AB=10,求四边形ADBE的面积;
(2)求证:BC=2AF.
【分析】(1)根据等腰直角三角形的性质可判定△ABD≌△ACE,则S△ABD=S△ACE,进而推出S四边形ADBE=S△ACE+S△ABE=S△ABC,再根据三角形的面积公式即可得解;
(2)过点A作AM⊥BC,垂足为点M,由(1)可推出AB平分∠CBF,得到AF=AM,再根据等腰三角形三线合一即可求解.
【解答】(1)解:∵∠BAC=∠DAE=90°,
∴∠BAD+∠BAE=∠CAE+∠BAE,
∴∠BAD=∠CAE,
∵△ABC与△ADE均为等腰直角三角形,
∴AB=AC,AD=AE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴S△ABD=S△ACE,
∵S四边形ADBE=S△ABD+S△ABE,
∴S四边形ADBE=S△ACE+S△ABE=S△ABC=?AB?AC=×102=50;
(2)证明:∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
由(1)知△ABD≌△ACE,
∴∠ABD=∠ACE=45°,
∴∠ABD=∠ABC,
即AB平分∠CBF,
过点A作AM⊥BC,垂足为点M,
∵AF⊥BF,
∴AF=AM,
又∵AB=AC,AM⊥BC,
∴BM=CM=BC,
∴AM=BC,
∴AF=BM,
∴BC=2AF.
一、选择题(共12小题).
1.若a>b,则下列不等式正确的是( )
A.3a<3b
B.ma>mb
C.﹣a﹣1>﹣b﹣1
D.+1>+1
2.下列语句是真命题的是( )
A.作∠AOB的平分线
B.若a2=b2,则a=b
C.四边形的内角和等于360°
D.不是对顶角不相等
3.下列描述的事件中,是随机事件的为( )
A.水能载舟,亦能覆舟
B.心想事成,万事如意
C.瓜熟蒂落,水到渠成
D.只手遮天,偷天换日
4.在一个不透明的盒子中装有n个球,其中红球有5个,它们除颜色外其它均相同.每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.05,那么可以推算出n的值大约是( )
A.100
B.500
C.1000
D.无法判断
5.如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F.若AB=DE,BC=BE,AC=BD,则∠ACB等于( )
A.∠E
B.∠D
C.∠BFC
D.∠DBE
6.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=70°,则∠1=( )
A.40°
B.20°
C.60°
D.70°
7.如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量相差( )
A.8g
B.10g
C.12g
D.15g
8.如图,已知∠ABC=60°,点D在边BA上,BD=10,点E,F在边BC上,DE=DF,若EF=4,则BE的长为( )
A.3
B.2.5
C.2
D.1.5
9.如图,AB∥CD,∠ABE=40°,若CF平分∠ECD,且满足CF∥BE,则∠ECD的度数为( )
A.70°
B.74°
C.78°
D.80°
10.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AE=AF;②AD垂直平分EF;③EF垂直平分AD;④AD平分∠EDF.其中正确的结论的个数为( )
A.1
B.2
C.3
D.4
11.如图,一张△ABC的纸片中,∠ACB=90°,BC=6,AB=10.在AC边上取一点E,将其沿着BE折叠,使点A与BC延长线上的点D重合,则CE的长为( )
A.4
B.3
C.2
D.1
12.如图,直线y=ax+4a(a≠0)与y=﹣x+b的交点的横坐标为﹣2,则关于x的不等式﹣x+b>ax+4a>0的整数解为( )
A.﹣1
B.﹣3
C.﹣4
D.﹣5
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.已知二元一次方程2x﹣7y=5,用含x的代数式表示y的等式为
.
14.“六一”节,小明去公园玩投掷飞镖的游戏.如图,圆形镖盘被等分成8部分,投中图中阴影部分有奖品.小明能获得奖品的概率是
.
15.如图所示,∠1=110°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
.
16.《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五,羊二,值金十两.牛二,羊五,值金八两.问牛羊各值金几何?”设牛,羊每头分别值金x两,y两,依题意,可列出方程组为
.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,射线BF⊥BC,垂足为点B,一动点E从C点出发以每秒1个单位长度的速度在线段CB上运动,点D为射线BF上一动点,随着E点运动而运动,且始终保持ED=AB,设点E运动时间为t(t>0)秒,当t=
秒时,△EDB与△ABC全等.
18.如图,已知等边△ABC.若以BC为一条边在其上方作等腰直角△BCD,则∠ABD的度数为
.
三、解答题(本大题共8个小题,满分66分)
19.解方程组.
20.解不等式组,然后把解集在数轴上表示出来,并写出不等式组的整数解.
21.在解关于x,y的方程组时,可以用①×7﹣②×3消去未知数x,也可以用①×2+②×5消去未知数y.
(1)求m和n的值;
(2)求原方程组的解.
22.如图,已知DE∥BC,∠3=∠B,求证:∠1+∠2=180°.
下面是小明同学不完整的证明过程,请你在横线上补充完整,并在括号里填上每一步的推理依据.
证明:∵DE∥BC(已知),
∴∠3=
(
).
∵∠3=∠B(
),
∴
=∠EHC(
).
∴AB∥EH(
).
∴∠2+
=180°(两直线平行,同旁内角互补).
∵∠1=∠4(
),
∴∠1+∠2=180°(
).
23.一个不透明袋子中装有红、黄、绿三种颜色的球共60个,它们除颜色外都相同.已知其中黄球个数是绿球个数的4倍,从袋中摸出一个球是红球的概率为.
(1)分别求红球和绿球的个数.
(2)求从袋中随机摸出一球是绿球的概率.
(3)从袋中拿出12个黄球,将剩余的球搅拌均匀,求从袋中剩余的球中随机摸出一个球是黄球的概率.
24.如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟时,甲、乙两人相距多少千米?
25.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
26.如图,△ABC与△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,连接BD,过点A作AF⊥BD交BD的延长线于点F.
(1)若AB=10,求四边形ADBE的面积;
(2)求证:BC=2AF.
参考答案
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1.若a>b,则下列不等式正确的是( )
A.3a<3b
B.ma>mb
C.﹣a﹣1>﹣b﹣1
D.+1>+1
【分析】根据不等式的性质逐一判断,判断出正确的不等式是哪个即可.
解:∵a>b,
∴3a>3b,
∴选项A不正确;
∵a>b,
∴m<0时,ma<mb;m=0时,ma=mb;m>0时,ma>mb,
∴选项B不正确;
∵a>b,
∴﹣a<﹣b,
∴﹣a﹣1<﹣b﹣1,
∴选项C不正确;
∵a>b,
∴>,
∴+1>+1,
∴选项D正确.
故选:D.
2.下列语句是真命题的是( )
A.作∠AOB的平分线
B.若a2=b2,则a=b
C.四边形的内角和等于360°
D.不是对顶角不相等
【分析】根据命题的概念、四边形的性质、对顶角的概念判断即可.
解:A、作∠AOB的平分线,没有对事件作出判断,不是命题,不符合题意;
B、若a2=b2,则a=±b,故原命题错误,是真命题,符合题意;
C、四边形的内角和为360°,本选项说法正确,是真命题,符合题意;
D、不是对顶角也可以相等,故本选项说法错误,是假命题,不符合题意;
故选:C.
3.下列描述的事件中,是随机事件的为( )
A.水能载舟,亦能覆舟
B.心想事成,万事如意
C.瓜熟蒂落,水到渠成
D.只手遮天,偷天换日
【分析】直接利用随机事件以及必然事件、不可能事件的定义分别分析得出答案.
解:A、水能载舟,亦能覆舟,是必然事件,故此选项不符合题意;
B、心想事成,万事如意,是随机事件,故此选项符合题意;
C、瓜熟蒂落,水到渠成,是必然事件,故此选项不符合题意;
D、只手遮天,偷天换日,是不可能事件,故此选项不符合题意.
故选:B.
4.在一个不透明的盒子中装有n个球,其中红球有5个,它们除颜色外其它均相同.每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.05,那么可以推算出n的值大约是( )
A.100
B.500
C.1000
D.无法判断
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解即可.
解:由题意可得,=0.05,
解得,n=100.
故估计n大约是100.
故选:A.
5.如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F.若AB=DE,BC=BE,AC=BD,则∠ACB等于( )
A.∠E
B.∠D
C.∠BFC
D.∠DBE
【分析】先根据SSS定理得出△ABC≌△DEB(SSS),即可根据全等三角形的性质得到∠ACB=∠DBE.
解:在△ABC与△DEB中,
,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE,
故选:D.
6.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=70°,则∠1=( )
A.40°
B.20°
C.60°
D.70°
【分析】先由题意可得:AB=AC,根据等边对等角的性质,可求得∠ACB的度数,又由直线l1∥l2,根据两直线平行,同旁内角互补即可求得∠1的度数.
解:根据题意得:AB=AC,
∴∠ACB=∠ABC=70°,
∵直线l1∥l2,
∴∠1+∠ACB+∠ABC=180°,
∴∠1=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°.
故选:A.
7.如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量相差( )
A.8g
B.10g
C.12g
D.15g
【分析】根据图可得:3块巧克力的重=2个果冻的重;1块巧克力的重+1个果冻的重=40g,由此可设出未知数,列出方程组解答.
解:设每块巧克力的重xg,每个果冻的重yg,由题意得:
,
解得:.
所以y﹣x=24﹣16=8(g),
即每块巧克力和每个果冻的重量相差8g.
故选:A.
8.如图,已知∠ABC=60°,点D在边BA上,BD=10,点E,F在边BC上,DE=DF,若EF=4,则BE的长为( )
A.3
B.2.5
C.2
D.1.5
【分析】过点D作DG⊥BC,垂足为G.利用等腰三角形的“三线合一”先求出EG,利用含30°角的直角三角形的边间关系,再求出BG,最后利用线段的和差关系求出BE.
解:过点D作DG⊥BC,垂足为G.
∵DE=DF,DG⊥BC,EF=4,
∴EG=EF=2.
在Rt△DBG中,∵∠ABC=60°,
∴∠BDG=30°.
∵DB=10,
∴BG=DB=5.
∴BE=BG﹣EG=3.
故选:A.
9.如图,AB∥CD,∠ABE=40°,若CF平分∠ECD,且满足CF∥BE,则∠ECD的度数为( )
A.70°
B.74°
C.78°
D.80°
【分析】如图,过E作EM∥AB,由EM∥AB,得∠B=∠BEM=40°.由AB∥CD,得EM∥CD,那么∠MEC+∠ECD=180°.由CF平分∠ECD,得∠ECF=.由BE∥CF,得∠BEC+∠ECF=180°,那么∠BEM+∠MEC+∠ECF=180°,故40°+180°﹣∠ECD+=180°,进而解决此题.
解:如图,过E作EM∥AB.
∵EM∥AB,
∴∠B=∠BEM=40°.
又∵AB∥CD,
∴EM∥CD.
∴∠MEC+∠ECD=180°.
∴∠MEC=180°﹣∠ECD.
∵CF平分∠ECD,
∴∠ECF=.
∵BE∥CF,
∴∠BEC+∠ECF=180°.
∴∠BEM+∠MEC+∠ECF=180°.
∴40°+180°﹣∠ECD+=180°.
∴∠ECD=80°.
故选:D.
10.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AE=AF;②AD垂直平分EF;③EF垂直平分AD;④AD平分∠EDF.其中正确的结论的个数为( )
A.1
B.2
C.3
D.4
【分析】根据角平分线性质求出DE=DF,证△AED≌△AFD,推出AE=AF,再逐个判断即可.
解:∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,∠ADE=∠ADF,
∴AD平分∠EDF;④正确;
∵AD平分∠BAC,
∵AE=AF,DE=DF,①正确;
∴AD垂直平分EF,②正确;③错误,
正确的有3个,
故选:C.
11.如图,一张△ABC的纸片中,∠ACB=90°,BC=6,AB=10.在AC边上取一点E,将其沿着BE折叠,使点A与BC延长线上的点D重合,则CE的长为( )
A.4
B.3
C.2
D.1
【分析】由勾股定理可求AC的长,由折叠的性质可得,BD=AB=10,EA=ED,利用勾股定理列方程求解即可.
解:由勾股定理得,AC===8,
由折叠的性质可得,BD=AB=10,EA=ED,
∴CD=BD﹣BC=10﹣6=4,
设CE=x,则EA=ED=8﹣x,
在Rt△DCE中,由勾股定理得,
x2+42=(8﹣x)2,
∴x=3,
故选:B.
12.如图,直线y=ax+4a(a≠0)与y=﹣x+b的交点的横坐标为﹣2,则关于x的不等式﹣x+b>ax+4a>0的整数解为( )
A.﹣1
B.﹣3
C.﹣4
D.﹣5
【分析】满足不等式﹣x+b>ax+4a>0就是直线y=﹣x+b位于直线y=ax+4a的上方且位于x轴的上方的图象,据此求得自变量的取值范围即可.
解:∵直线y=ax+4a(a≠0)与y=﹣x+b的交点的横坐标为﹣2,
∴关于x的不等式﹣x+b>ax+4a的解集为x<﹣2,
∵y=ax+4a=0时,x=﹣4,
∴ax+4a>0的解集是x>﹣4,
∴﹣x+b>ax+4a>0的解集是﹣4<x<﹣2,
∴关于x的不等式式﹣x+b>ax+4a>0的整数解为﹣3.
故选:B.
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.已知二元一次方程2x﹣7y=5,用含x的代数式表示y的等式为
y= .
【分析】先移项,再把y的系数化为1即可.
解:移项得,7y=2x﹣5,
y的系数化为1得,y=.
故答案为:y=.
14.“六一”节,小明去公园玩投掷飞镖的游戏.如图,圆形镖盘被等分成8部分,投中图中阴影部分有奖品.小明能获得奖品的概率是
.
【分析】用阴影部分的份数除以总份数即可求得获得奖品的概率.
解:∵飞镖盘被平均分成8份,阴影部分占4份,
∴小明能获得奖品的概率是=.
故答案为:.
15.如图所示,∠1=110°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
220° .
【分析】连接EF,由三角形的内角和定理可求得∠A+∠D+∠CFD+∠AEB=∠BEF+∠CFE,利用三角形外角的性质可得∠1=∠B+∠C=∠BEF+∠CFE=∠A+∠D+∠CFD+∠AEB,进而可求解.
解:连接EF,
∵∠A+∠D+∠3=∠AEF+∠DFE+∠2=180°,∠2=∠3,
∴∠A+∠D=∠AEF+∠DFE,
∴∠A+∠D+∠CFD+∠AEB=∠AEF+∠DFE+∠CFD+∠AEB=∠BEF+∠CFE,
∵∠1=∠B+∠C=∠BEF+∠CFE,
∴∠A+∠D+∠CFD+∠AEB=∠1,
∵∠1=110°,
∴∠A+∠B+∠C+∠D+∠AEB+∠CFD=2∠1=220°,
16.《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五,羊二,值金十两.牛二,羊五,值金八两.问牛羊各值金几何?”设牛,羊每头分别值金x两,y两,依题意,可列出方程组为
.
【分析】因为每头牛值金x两,每头羊值金y两,根据“牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两”,即可得出关于x、y的二元一次方程组,此题得解.
解:因为每头牛值金x两,每头羊值金y两,
根据题意得:.
故答案为:.
17.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,射线BF⊥BC,垂足为点B,一动点E从C点出发以每秒1个单位长度的速度在线段CB上运动,点D为射线BF上一动点,随着E点运动而运动,且始终保持ED=AB,设点E运动时间为t(t>0)秒,当t= 2 秒时,△EDB与△ABC全等.
【分析】当BE=CA或BE=CB时,由HL得△EDB与△ABC全等,则4﹣t=2或4﹣t=4,即可求解.
解:∵BF⊥BC,
∴∠EBD=90°,
∵∠ACB=90°,ED=AB,
∴当BE=CA或BE=CB时,△EDB与△ABC全等,
∴4﹣t=2或4﹣t=4,
解得:t=2或t=0,
∵t>0,
∴t=2,
即当t=2秒时,△EDB与△ABC全等,
故答案为:2.
18.如图,已知等边△ABC.若以BC为一条边在其上方作等腰直角△BCD,则∠ABD的度数为 15°或30° .
【分析】分情况讨论,分别以BC为底边或腰在其上方作等腰直角△BCD,分别画图,即可得到∠ABD的度数.
解:如图1所示,∠ABD=∠CBD﹣∠ABC=90°﹣60°=30°;
如图2所示,∠ABD=∠ABC﹣∠DBC=60°﹣45°=15°;
如图3所示,∠ABD=∠ABC﹣∠DBC=60°﹣45°=15°;
故答案为:15°或30°.
三、解答题(本大题共8个小题,满分66分)
19.解方程组.
【分析】方程组利用代入消元法求出解即可.
解:,
将①代入②得:11x=33,
解得:x=3,
将x=3代入①得:y=3,
则方程组的解为.
20.解不等式组,然后把解集在数轴上表示出来,并写出不等式组的整数解.
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分求出不等式组的解集,表示在数轴上,确定出整数解即可.
解:,
由①得,x>﹣2,
由②得,x≤1,
∴不等式组的解集是﹣2<x≤1,
解集在数轴上表示如图:
∴不等式组的整数解是﹣1,0,1.
21.在解关于x,y的方程组时,可以用①×7﹣②×3消去未知数x,也可以用①×2+②×5消去未知数y.
(1)求m和n的值;
(2)求原方程组的解.
【分析】(1)利用①×7﹣②×3消去未知数x得到7(m+1)=3(n+2),利用①×2+②×5得到﹣2n+5m=0,然后解关于m、n的方程组即可;
(2)由(1)得到,然后利用加减消元法解方程组.
解:(1)根据题意得,解得;
(2)原方程组为,
①×7﹣②×3得﹣35y﹣6y=123,
解得y=﹣3,
把y=﹣3代入②得7x﹣6=1,
解得x=1,
所以原方程组的解为.
22.如图,已知DE∥BC,∠3=∠B,求证:∠1+∠2=180°.
下面是小明同学不完整的证明过程,请你在横线上补充完整,并在括号里填上每一步的推理依据.
证明:∵DE∥BC(已知),
∴∠3= ∠EHC (
两直线平行,内错角相等 ).
∵∠3=∠B(
已知 ),
∴ ∠B =∠EHC(
等量代换 ).
∴AB∥EH(
同位角相等,两直线平行 ).
∴∠2+ ∠4 =180°(两直线平行,同旁内角互补).
∵∠1=∠4(
对顶角相等 ),
∴∠1+∠2=180°(
等量代换 ).
【分析】由平行线的性质可得∠3=∠EHC,从而有∠B=∠EHC,则可判断AB∥EH,根据平行线的性质有∠2+∠4=180°,即可得证.
【解答】证明:∵DE∥BC(已知),
∴∠3=∠EHC(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠EHC(等量代换),
∴AB∥EH(同位角相等,两直线平行),
∴∠2+∠4=180°(两直线平行,同旁内角互补),
∵∠1=∠4(对顶角相等),
∴∠1+∠2=180°(等量代换).
故答案为:∠EHC;两直线平行,内错角相等;已知;等量代换;同位角相等,两直线平行;∠4;对顶角相等;等量代换.
23.一个不透明袋子中装有红、黄、绿三种颜色的球共60个,它们除颜色外都相同.已知其中黄球个数是绿球个数的4倍,从袋中摸出一个球是红球的概率为.
(1)分别求红球和绿球的个数.
(2)求从袋中随机摸出一球是绿球的概率.
(3)从袋中拿出12个黄球,将剩余的球搅拌均匀,求从袋中剩余的球中随机摸出一个球是黄球的概率.
【分析】(1)根据红、黄、白三种颜色球共有的个数乘以红球的概率即可求得红球的个数,设绿球有x个,则黄球有2x个,根据球的总个数列出方程求出x的值即可得;
(2)用绿球的个数除以总的球数即可;
(3)先求出从袋中拿出4个黄球还剩的球数,再根据红球的个数,除以还剩的球数即可.
解:(1)红球个数:60×=20(个),
设绿球有x个,则黄球有4x个,
根据题意,得x+4x+20=60,
解得x=8,
所以红球有20个,绿球有8个,
(2)从袋中随机摸出一球,共有60种等可能的结果,其中摸出绿球的结果有8种,
所以从袋中随机摸出一球是绿球的概率为=;
(3)由(1)得4x=32,拿出12个黄球以后,从袋中随机摸出一球,共有48种等可能的结果,其中摸出黄球的结果有20种,
所以从袋中剩余的球中随机摸出一个球是黄球的概率=.
24.如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟时,甲、乙两人相距多少千米?
【分析】(1)分别根据甲、乙的图象计算出各自的速度即可求出S甲、S乙与t之间的关系式;
(2)把t=10代入解析式进而解答即可.
解:(1)由图象设甲的解析式为:S甲=kt,代入点(24,12),解得:k=0.5;
所以甲的解析式为:S甲=0.5t;
同理可设乙的解析式为:S乙=mt+b,代入点(6,0),(18,12),
可得:,
解得:,
所以乙的解析式为S乙=t﹣6;
(2)当t=10时,S甲=0.5×10=5(千米),S乙=10﹣6=4(千米),
5﹣4=1(千米),
答:甲行驶10分钟时,甲、乙两人相距1千米.
25.某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【分析】(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号4台B型号的电扇收入1200元,5台A型号6台B型号的电扇收入1900元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台,根据金额不多余7500元,列不等式求解;
(3)根据A种型号电风扇的进价和售价、B种型号电风扇的进价和售价以及总利润=一台的利润×总台数,列出不等式,求出a的值,再根据a为整数,即可得出答案.
解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:,
解得:,
答:A、B两种型号电风扇的销售单价分别为200元、150元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台.
依题意得:160a+120(50﹣a)≤7500,
解得:a≤37.
答:超市最多采购A种型号电风扇37台时,采购金额不多于7500元.
(3)根据题意得:
(200﹣160)a+(150﹣120)(50﹣a)>1850,
解得:a>35,
∵a≤37,且a应为整数,
∴在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种:
当a=36时,采购A种型号的电风扇36台,B种型号的电风扇14台;
当a=37时,采购A种型号的电风扇37台,B种型号的电风扇13台.
26.如图,△ABC与△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,连接BD,过点A作AF⊥BD交BD的延长线于点F.
(1)若AB=10,求四边形ADBE的面积;
(2)求证:BC=2AF.
【分析】(1)根据等腰直角三角形的性质可判定△ABD≌△ACE,则S△ABD=S△ACE,进而推出S四边形ADBE=S△ACE+S△ABE=S△ABC,再根据三角形的面积公式即可得解;
(2)过点A作AM⊥BC,垂足为点M,由(1)可推出AB平分∠CBF,得到AF=AM,再根据等腰三角形三线合一即可求解.
【解答】(1)解:∵∠BAC=∠DAE=90°,
∴∠BAD+∠BAE=∠CAE+∠BAE,
∴∠BAD=∠CAE,
∵△ABC与△ADE均为等腰直角三角形,
∴AB=AC,AD=AE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴S△ABD=S△ACE,
∵S四边形ADBE=S△ABD+S△ABE,
∴S四边形ADBE=S△ACE+S△ABE=S△ABC=?AB?AC=×102=50;
(2)证明:∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
由(1)知△ABD≌△ACE,
∴∠ABD=∠ACE=45°,
∴∠ABD=∠ABC,
即AB平分∠CBF,
过点A作AM⊥BC,垂足为点M,
∵AF⊥BF,
∴AF=AM,
又∵AB=AC,AM⊥BC,
∴BM=CM=BC,
∴AM=BC,
∴AF=BM,
∴BC=2AF.
同课章节目录
