华东师大版七年级数学上册3.3.2多项式课件(20张ppt)
文档属性
| 名称 | 华东师大版七年级数学上册3.3.2多项式课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 302.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
多
项
式
多
项
式
多
项
式
1、了解多项式、项、次数等相关概念;
2、归纳总结整式、单项式、多项式三者之间的联系与区别;
3、学会列多项式,熟悉多项式求值在具体问题中的应用。
学习目标
掌握多项式的相关概念。
重点
会确定一个多项式的项数和次数。
难点
重难点
问题
(1)若三角形的三条边长分别为a、b、c,则三角形的周长是___________;
(2)某班有男生x人,女生21人,这个班的学生一共有_______人;
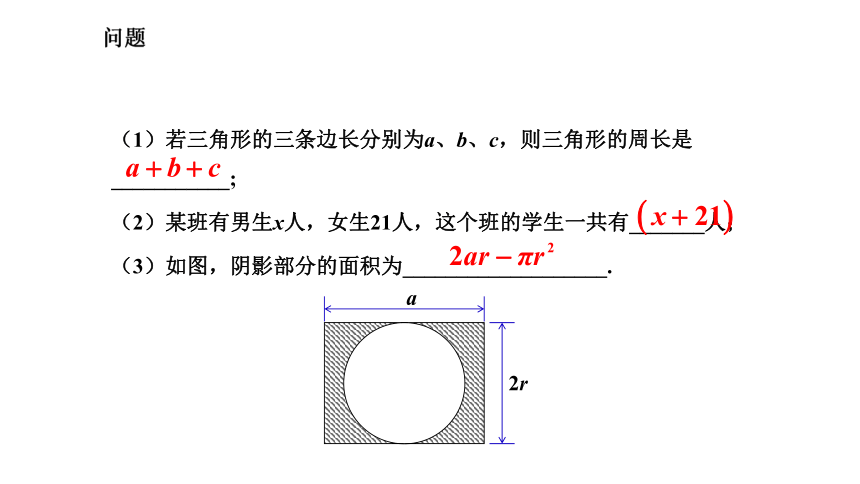
(3)如图,阴影部分的面积为___________________.
2r
a
观察下列式子:
思考
思考:这些式子有什么特点?
这些式子都可以看作几个单项式的和。例如:
a
+
b
+
c
可以看作单项式a、b与c的和;
2arπr2
可以看作单项式2ar与πr2的和。
像这样,几个单项式的和叫做多项式。
其中,每个单项式叫做多项式的项。
不含字母的项叫做常数项。
例如,多项式3x22x5的项是3x2、2x与5,其中,5是常数项。
多项式
下列哪些式子是单项式?哪些是多项式?
,0.8p+mn,a2h,3,x+yz,ab+bc+cd,a31
多项式:0.8p+mn,x+yz,ab+bc+cd,a31.
单项式:,a2h,3.
练习
例如,多项式
x2+2x+18
中次数最高项是二次项
x2,这个多项式的次数是2。
多项式里,次数最高项的次数,叫做这个多项式的次数。
一般的,我们称
x2+2x+18
为二次三项式。
次数
一个多项式含有几项,就叫做几项式。
指出下列多项式的项和次数:
解:
(2)多项式的项有、、
,次数是4;
例2
(1)多项式的项有、
、、
,次数是3;
多项式的每一项都包括它的正负号.
(1)x3x+1;
(2)x32x2y2+3y2.
指出下列多项式是几次几项式:
解:(1)x3x+1是三次三项式;
(2)x32x2y2+3y2是四次三项式.
要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的.
例3
多项式的各项应包括它前面的符号;
要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
一个多项式的最高次项可以不唯一.
多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
小结
整式
单项式与多项式统称为整式。
整式
单项式
多项式
数或字母相乘
几个单项式相加
下列式子中,哪些是单项式?哪些是多项式?哪些是整式?
3x,2x1,
,ab,5,
,3m4nm2n.
单项式
多项式
整式
3x
ab
5
2x1
3m4nm2n
3x
ab
5
2x1
3m4nm2n
练习
指出下列多项式是几次几项式:
二次三项式
四次二项式
二次三项式
三次三项式
随堂练习
1.多项式2x
+
3yz是单项式______,______,_____的和,它是
_____次_____项式.
2.多项式3m33m6m2的常数项是______,一次项是_____,
二次项的系数是_____.
2x
3y
z
一
三
6
3m
1
基础巩固
3.一个关于字母x的二次三项式的二次项系数为2,一次项系数为3,常数项为8,则这个二次三项式为____________________.
2x2+3x+8
基础巩固
4.已知是关于x的三次三项式,那么m的值为(
)
A.3
B.4
C.5
D.6
B
5.若关于x,y的多项式是三次三项式,
则m等于(
)
A.-1
B.0
C.1
D.±1
6.请写出一个单项式,同时满足下列条件:①含有字母x、y;②系数是负整数;③次数是4,你写的单项式为______.
C
xy3
答案不唯一
基础巩固
7.下列说法错误的是
(
)
A.
是二次三项式
B.
不是单项式
C.
的系数是
D.的次数是6
8.下列代数式中:中,整式有(
)个
A.3个
B.4个
C.5个
D.6个
D
B
基础巩固
多项式和整式的相关概念
知识
考点
课堂总结
判断多项式的次数和项数
多项式
多
项
式
多
项
式
多
项
式
1、了解多项式、项、次数等相关概念;
2、归纳总结整式、单项式、多项式三者之间的联系与区别;
3、学会列多项式,熟悉多项式求值在具体问题中的应用。
学习目标
掌握多项式的相关概念。
重点
会确定一个多项式的项数和次数。
难点
重难点
问题
(1)若三角形的三条边长分别为a、b、c,则三角形的周长是___________;
(2)某班有男生x人,女生21人,这个班的学生一共有_______人;
(3)如图,阴影部分的面积为___________________.
2r
a
观察下列式子:
思考
思考:这些式子有什么特点?
这些式子都可以看作几个单项式的和。例如:
a
+
b
+
c
可以看作单项式a、b与c的和;
2arπr2
可以看作单项式2ar与πr2的和。
像这样,几个单项式的和叫做多项式。
其中,每个单项式叫做多项式的项。
不含字母的项叫做常数项。
例如,多项式3x22x5的项是3x2、2x与5,其中,5是常数项。
多项式
下列哪些式子是单项式?哪些是多项式?
,0.8p+mn,a2h,3,x+yz,ab+bc+cd,a31
多项式:0.8p+mn,x+yz,ab+bc+cd,a31.
单项式:,a2h,3.
练习
例如,多项式
x2+2x+18
中次数最高项是二次项
x2,这个多项式的次数是2。
多项式里,次数最高项的次数,叫做这个多项式的次数。
一般的,我们称
x2+2x+18
为二次三项式。
次数
一个多项式含有几项,就叫做几项式。
指出下列多项式的项和次数:
解:
(2)多项式的项有、、
,次数是4;
例2
(1)多项式的项有、
、、
,次数是3;
多项式的每一项都包括它的正负号.
(1)x3x+1;
(2)x32x2y2+3y2.
指出下列多项式是几次几项式:
解:(1)x3x+1是三次三项式;
(2)x32x2y2+3y2是四次三项式.
要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的.
例3
多项式的各项应包括它前面的符号;
要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
一个多项式的最高次项可以不唯一.
多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
小结
整式
单项式与多项式统称为整式。
整式
单项式
多项式
数或字母相乘
几个单项式相加
下列式子中,哪些是单项式?哪些是多项式?哪些是整式?
3x,2x1,
,ab,5,
,3m4nm2n.
单项式
多项式
整式
3x
ab
5
2x1
3m4nm2n
3x
ab
5
2x1
3m4nm2n
练习
指出下列多项式是几次几项式:
二次三项式
四次二项式
二次三项式
三次三项式
随堂练习
1.多项式2x
+
3yz是单项式______,______,_____的和,它是
_____次_____项式.
2.多项式3m33m6m2的常数项是______,一次项是_____,
二次项的系数是_____.
2x
3y
z
一
三
6
3m
1
基础巩固
3.一个关于字母x的二次三项式的二次项系数为2,一次项系数为3,常数项为8,则这个二次三项式为____________________.
2x2+3x+8
基础巩固
4.已知是关于x的三次三项式,那么m的值为(
)
A.3
B.4
C.5
D.6
B
5.若关于x,y的多项式是三次三项式,
则m等于(
)
A.-1
B.0
C.1
D.±1
6.请写出一个单项式,同时满足下列条件:①含有字母x、y;②系数是负整数;③次数是4,你写的单项式为______.
C
xy3
答案不唯一
基础巩固
7.下列说法错误的是
(
)
A.
是二次三项式
B.
不是单项式
C.
的系数是
D.的次数是6
8.下列代数式中:中,整式有(
)个
A.3个
B.4个
C.5个
D.6个
D
B
基础巩固
多项式和整式的相关概念
知识
考点
课堂总结
判断多项式的次数和项数
多项式
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
